中考命题“高观点”，解题教学宜拓展——2015年河南卷第23题思路突破与解后反思

☉江苏省南通市易家桥中学 徐向清

中考命题“高观点”，解题教学宜拓展
——2015年河南卷第23题思路突破与解后反思

☉江苏省南通市易家桥中学 徐向清

近读期刊，有老师就2015年隐含考查所谓抛物线“准线”、“焦点”问题，笔者研习2015年全国各地中考卷时，关注到2015年河南卷最后一题，从高观点看，也是一道涉及“准线”、“焦点”问题.本文先呈现该题的思路突破，再给出问题结构的反思，与同行研讨.

一、考题及思路突破

图1

考题（2015年河南卷，第23题）如图1，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F，点D、E的坐标分别为（0，6）、（-4，0），连接PD、PE、DE.

（1）请直接写出抛物线的解析式；

（2）小明探究点P的位置时发现：当点P与点A或点C重合时，PD与PF的差为定值，进而猜想：对于任意一点P，PD与PF的差为定值，请你判断该猜想是否正确，并说明理由；

（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点”的坐标.

（3）在点P运动时，DE大小不变，则PE与PD的和最小时，△PDE的周长最小，由第（2）问可知，PD-PF=2，有PD=PF+2，于是PE+PD=PE+PF+2，也就是当P、E、F三点共线时，PE+PF最小，此时点P，E的横坐标都为-4，将x= -4代入8，得y=6，所以（-4，6），此时△PDE的周长最小，且△PDE的面积为12，点P恰为“好点”.即△PDE的周长最小时“好点”的坐标为（-4，6）.

上面其实是从特例角度通过计算验证出一个“好点”的位置，也顺便把其中一个问题解答了.然而要想探究“好点”个数还有较长的路要走！

图2

图3

在图3中，△PDE的面积可以用△PDQ的面积减去△PEQ的面积求出，经过整理、化简、配方仍然有S△PDE=

这时结合a的取值范围：-8≤a≤0，根据S关于a的二次函数增减性，数形结合地分析出4≤S△PDE≤13，于是△PDE的面积可以等于4到13内所有整数有10个，容易忽略的是在面积为12时，a的值有两个，所以面积为整数时“好点”有11个，经过验证周长最小的“好点”包含这11个点之内，所以好点共11个.

二、解后反思

1.第（2）问的“深层结构”

上面在第（2）问解法突破时，用相同的参数a，构造直角三角形表示出PD、PF的长，从而发现它们之间的数量关系，这里的难点还在于二次根式的化简.事实上，如果熟悉高中阶段提及的“两点间距离公式”，则可绕开构造直角三角形的麻烦，直接求出PD的长；还有，如果认识深刻的话，还可发现这里隐藏着抛物线的“焦点”问题，即点D就是抛物线的焦点，而准线就是直线y=10，构造图4.

图4

根据抛物线准线、焦点的性质，很容易洞察这里的问题结构，抛物线上任意一点P到焦点D、准线y=10的距离相等，即PD=PG.而FG始终是一定值2，也就是PF+2= PD，即PD与PF的差为定值2.

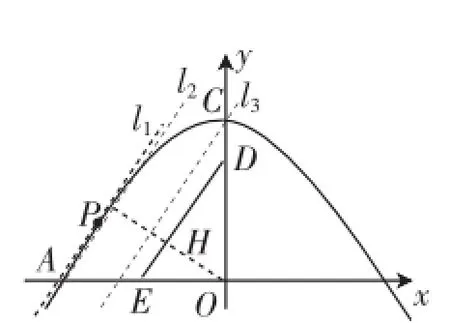
图5

2.第（3）问的“直观”解法

如图5，平移直线DE，与抛物线相交于三个特殊位置（如图5中的直线l1与抛物线相切于点P，直线l2与抛物线有一个交点恰为A点，直线l3经过抛物线顶点C，此时计算出原点O到直线l1、l2、l3的距离分别足条件的点P到DE的距离（即△PDE中DE边上的高）在这时当分子在整数4～13内，△PDE的面积为整数，又高△PDE有两个点P符合，所以一共有11个“好点”.

三、命题导向与教学启示

1.立足高观点，构思“初等”问题

从上面的求解来看，河南卷这道压轴题的第（2）、（3）问都属于“高观点”下抛物线的认识，如果有高中阶段准线、焦点的知识储备，则可一眼洞穿第（2）问，获得思路的快速突破；如果有直线平移与抛物线相交、相切的认识，则可快速获得第（3）问的直观化思考.以笔者所见，这类考题在近年来的各地中考试题中还不是个例，一方面可能与中考命题题组中至少包含一名高中数学教师有关，另一方面也传递了一种命题导向：基于高观点，构思初等问题.

2.课标是底线，解题教学宜拓展

我们知道，《义务教育数学课程标准（2011年版）》对二次根式运算化简、二次函数教学的要求并没有达到河南省考题的高度，如果以课标刚性标准来衡量，考题确实有“超标”之嫌，值得商榷.然而，作为平时解题教学，也应该获得不少启示，比如，解题教学应该倡导反思，在反思中成果扩大，变式拓展，注意对问题深层结构的揭示，促进优秀学生深刻理解.事实上，专家教师、南通市启秀中学李庾南老师就曾表达过“课标是底线要求，不是天花板”的观点.

1.罗增儒.数学解题学引论［M］．西安：陕西师范大学出版社，2008.

2.中华人民共和国教育部制定．义务教育数学课程标准（2011年版）［M］．北京：北京师范大学出版社，2012．

3.鲍建生，顾泠沅，等.变式教学研究［J］．数学教学，2003（1，2，3）．

4.贺信淳．从多角度审视一道中考试题说开去——谈对初中数学教育现状之惑［J］．数学通报，2013（12）.

5.夏再迅．试题改编需要理解深层结构——由一道几何考题的求解说起［J］．中学数学（下），2013（12）