专题复习课：值得尝试的一种复习课型

☉浙江省宁波市第七中学 蔡友山

专题复习课：值得尝试的一种复习课型

☉浙江省宁波市第七中学 蔡友山

近读《中学数学》，杨峰老师在文1中以等边三角形为载体，渐次展开变式生长，如“万花筒”般地呈现了一节优秀的复习课例，笔者恰好在八年级任教，直接拿来就在所教班级上过该课，效果很好．受到启发，我们备课组也认真研讨了复习课到底该如何组织习题素材，改变过去大量习题的教案编制取向，追求简约的呈现形式．以下先给出我们关于角平分线和垂直平分线专题复习课的教学设计，并逐项解读设计意图，提供研讨．

一、“角平分线与线段垂直平分线”专题复习课教学设计

1.基础练习

（1）如图1，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA=5，则线段PB的长度为_______．

图1

图2

（2）如图2，射线OC平分∠AOB，点P在OC上，且PM⊥OA于点M，PN⊥OB于点N．当PM=2cm时，PN= ________cm．理由是______________________________．

（3）如图3，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，BC=9，BD=5，则点D到AB的距离为________．

图3

图4

（4）如图4，ED是AB的垂直平分线，且CE=3，AC=8，连接BE，则BE=________.

设计要求：数学复习是否需要罗列一些概念或性质定理，近似文科默写那样的形式，仍然有所争议，笔者通过上述4道小题，以小题训练的方式复习几何概念与性质是值得尝试的方法．然而需要强调的是，开课阶段以小题方式复习概念或基本性质时，这些小题务必十分简单，让班级一半的学生能不动笔就可以直接口算解答，而且4个小题的答题时间控制在4分钟以内．

2.典例讲评

例1如图5，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，延长AE交BC的延长线于点F．若BE⊥AE．求证：BA=BF.

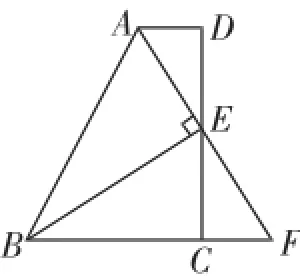
图5

教学意图：这类经典习题学生在相关教辅资料上都练习过原型问题，这里安排学生先独立思考之后，讲解思路，再安排另外的学生重复讲解思路，追求基础问题多数学生都能过关．

例2在△ABC中，若AD是∠BAC的平分线，点E和点F分别在AB和AC上，且DE⊥AB，垂足为E，DF⊥AC，垂足为F（如图6），则可以得到以下两个结论：①∠AED+∠AFD=180°；②DE=DF．那么在△ABC中，仍然有条件“AD是∠BAC的角平分线，点E和点F分别在AB和AC上”，请探究问题：若∠AED+∠AFD=180°（如图7），分析DE与DF的数量关系？说明理由．

图6

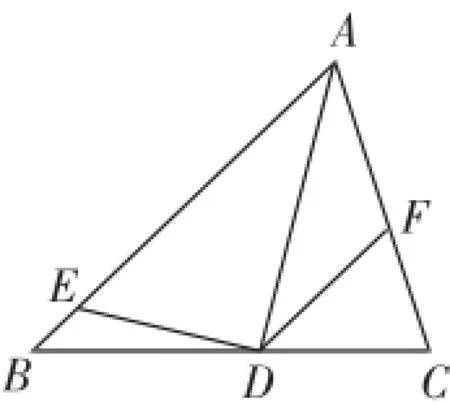
图7

教学意图：成功求解该题需要克服几个障碍，比如过点D作出AB、AC的垂线段DG、DH，垂足分别为G、H；接着是另一个较难点：发现∠GDH+∠EAF=180°，∠EDF+∠EAF=180°，从而得出∠EDG=∠FDH，可证△EDG≌△FDH，问题获得突破．

3.巩固练习

（1）如图8，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（）.

A．1B．2C．3D．4

图8

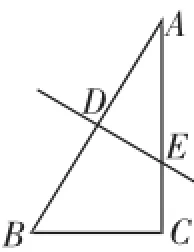
图10

图9

（2）如图9，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是_________．

（3）如图10，AB的垂直平分线分别交AB、AC于点D、E，AC=9，AE∶EC=2∶1.则点B到点E的距离是_________.

（4）如图11，已知△ABC.

①在AB上求作一点M，使点M到A、C两点的距离相等；

②在AB上求作一点N，使点N到AC、BC的距离相等．

（要求：用尺规作图，保留作图痕迹，不写作法）

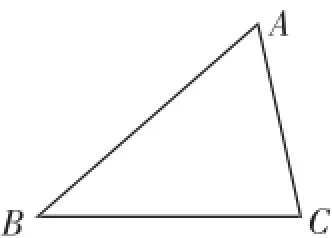
图11

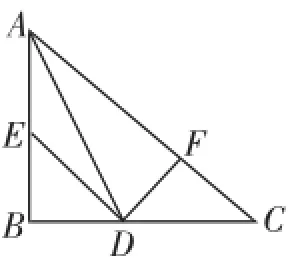
图12

（5）如图12，在△ABC中，∠B=90°，DF⊥AC，垂足为F，在AB上截取BE=CF，连接DE，并有DE=DC．

①求证：AD是△ABC的角平分线；

②作BH⊥AC于点H，交AD于点G，判断△BGD的形状，并说明理由．

设计解读：这里5道小题预设答题时间10分钟，5分钟讲评并统计正确率．题型依次为选择题1道、填空题2道、解答题2道，其中前4题都是简单题，让二分之一学生读题之后就有思路，直接下手解答，这样才能赢得6分钟解答第5题，而二分之一学生可能只有机会做到第5题的第（1）问练习时间就到了，这也符号当前各级数学考试限时完成的规律，让优秀学生学会提高解题效率．同时稍难题只能放在第5题的最后一问，符合各级考试中的把关题风格，用来控制满分，促进优秀学生深入思考、挑战高分．

二、关于“专题复习课”的相关思考

应该承认，当前的初中数学课堂中复习课占据很大的份量，月考前有复习课，单元复习时有复习课，期中、期末有复习课，中考前有复习课，而这些复习课中常常都是以某个单元或某章为课时的复习主题，其结果是反复练、重复练，“重要的事情反复说”，让备考师生都感到倦怠和厌烦，一线教师常常有这样的感觉，“复习课是会的还会，不会的还不会”．这也是我们全貌展示备课组内经过研讨之后的专题复习课教学设计的原因，即将复习课设计成专题复习课，打破教材章节限制，将同类型的、可以聚集在一个主题之下的知识点、题型或思想方法归类研究，引导学生从另一角度思考之前练习过的多个知识点、基本图形，这样也许可以追求专题复习课真正走上“老歌新唱”之效果．以下就围绕相关话题给出进一步的思考．

1.专题复习课重在构思主题，聚焦复习主题是关键

由于专题复习课并不是教材上规定的内容，所以需要教师基于专业理解，对复习内容的整体构思，优选专题内容，并在此基础上组织复习素材（即典型习题）．从上面的课例可见，我们确定复习主题为角平分线与线段垂直平分线，这两个内容分布在不同知识单元，但是它们本质上具有很多结构上的相似，比如，它们的概念、性质定理、判定定理，它们的尺规作图等都可从动点轨迹的角度来认识；所以开展这样的专题复习课对于学生深刻理解这两个几何概念是十分有益的．

2.专题复习课从基础题出发，预设变式追问重对话

常常看到一些专题复习课挑选一些较复杂的中考综合题作为例题，然后整节课带领学生在这些难题中沉浮，结果很多数学适应性不好的学生不知所云，消耗一节课时间，而优秀学生也容易似懂非懂，缺少对问题本质或结构的深刻认识．所以，我们认为专题复习课应该坚持从基础题出发，像上文中的教学设计中三个栏目一样，开课阶段“基础练习”绝对是基础题，优秀学生口算直接获得答案；例题讲评时的第（1）问是引导上路，不能太难，要让班级二分之一的学生都能上手直接获得思路；尽管在最后一个栏目“巩固练习”中，我们也仍然强调选题的基础性，前4道要让80%的学生都能做对，把真正的难题放置在第5题的第（2）问，让优秀学生拾阶而上，挑战满分．

1.郑毓信．多元表征理论与概念教学［J］．小学数学教育，2011（10）.

2.郑毓信．多元表征理论与概念教学（续）［J］．中学数学教学参考（上），2011（6）.

3.李袆．高水平数学教学到底该教什么［J］．数学教育学报，2014（6）.

4.马立平，著.小学数学的掌握和教学［M］．李士锜，吴颖康，等，译．上海：华东师范大学出版社，2011