基于遗传算法的直流伺服系统PID 参数优化*＊

范晋伟 唐宇航 闫洪霞 袁 帅

(北京工业大学机电学院，北京 100124)

伺服系统的性能直接影响和决定CNC 系统的快速性、稳定性和准确性。以伺服电动机为驱动元件的伺服系统是数控装置与机床的重要连接环。

PID 控制是工业过程控制中应用最广泛的策略之一。目前的PID 参数优化方法主要包括间接寻优法、专家整定法和单纯形法等［1］。单纯形法对初值敏感，易陷入局部最优解。专家整定法需要大量经验，不同的经验对应不同的目标函数。总结文献资料，遗传算法克服了单纯形法的初值敏感性且不需复杂规则，操作方便快速。

本研究旨在建立数控机床传动系统与电气驱动系统的机电匹配模型，采用计算机建模对机床伺服进给系统的动态特性进行分析，得到各参数对系统动态特性影响的定性分析后，利用遗传算法对系统调节器的参数进行全局优化。

1 直流伺服控制系统建模及模型分析

1.1 直流伺服电动机数学模型分析

令电动机负载扰动Td(s)=0，直流伺服电动机传递函数模型为:

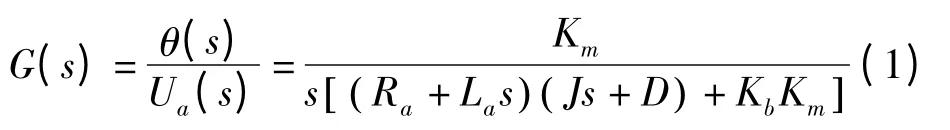
式中:Km为磁性材料的磁导率函数;Ra为电枢直流电阻;La为电枢电感;J 为电动机转动惯量;D 为电动机粘滞阻尼;θ 为电动机输出角度;Kb为电动机反电势常数。

1.2 三环控制系统模型分析

在伺服控制系统中，为保证精确性，输出量的反馈控制不可或缺。依由内向外的设计顺序，以及各环节的设计要求，获得简化的三环控制模型。

一般情况下电流环要求有很好的跟随性能，超调小，故选用典型的I 型系统。获得其等效传递函数为:

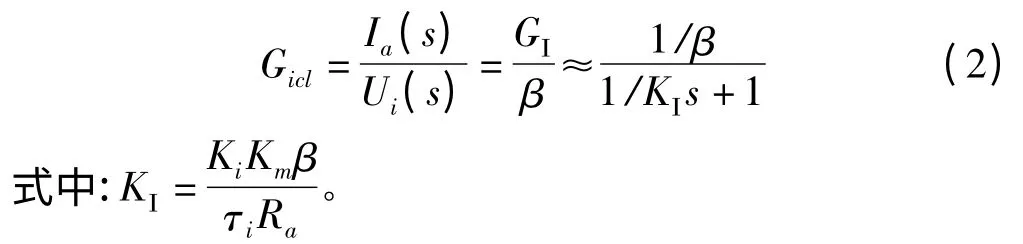
速度环反馈取电动机转速为输出节点。系统转速输入要求动态性能好，稳态时无静差。将电流环用其等效传递函数代替。为满足系统无静差要求，速度环按Ⅱ型系统设计，获得速度环等效传递函数为:

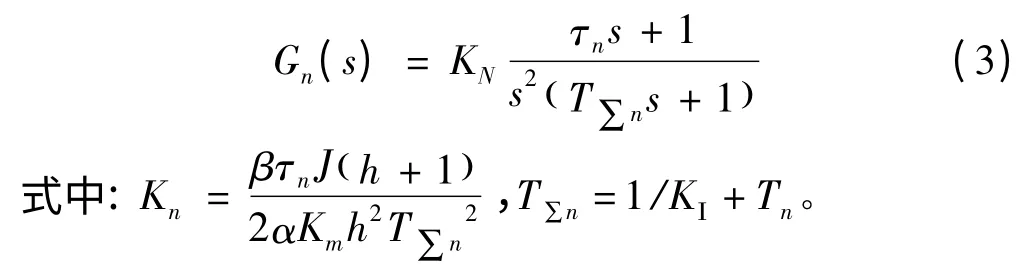
将速度环信号经积分即可获得位置信号。位置信号要求稳态无静差。传递函数为:

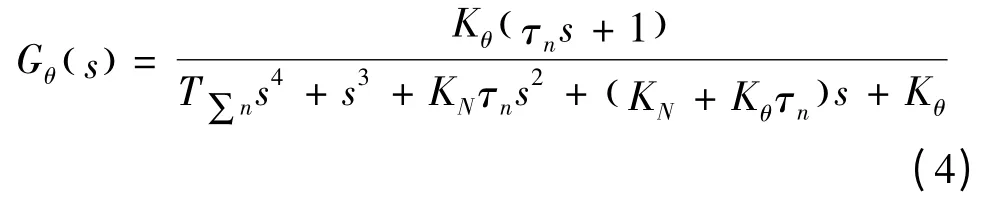
2 PID 参数的初步整定

2.1 参数选取

以北京数控设备厂FB -15 型直流伺服电动机数据(表1)为例进行仿真，其参数如下［2］:

要求系统无静态误差，电流超调量σi≤5%，空载启动到额定转速时的转速超调量σn≤10%。

该电动机晶闸管调速系统采用三相桥式装置整流，晶闸管放大系数Ks=40。其滞后时间常数Ts=三相桥式电路平均失控时间=0.001 7 s，所需基本滤波时间为T0i=2 ms=0.002 s。故，按小时间常数近似处理，得:

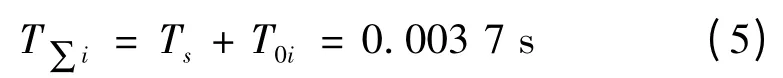
根据设计手册，当σi≤5%时，KIT∑i=0.5 。由式(2)得电流环比例系数:

根据设计手册，该电动机速度环滤波时间常数Tn=0.01 s。

取速度环小时间常数:

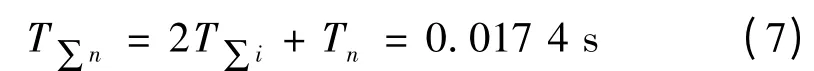
按照抗干扰性能较好的原则，取h=5，得速度环积分时间常数:

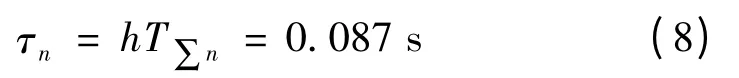
因此，由式(3)，速度环比例系数为:

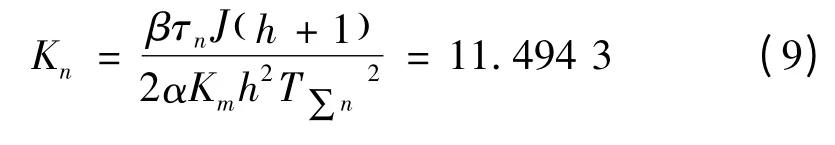
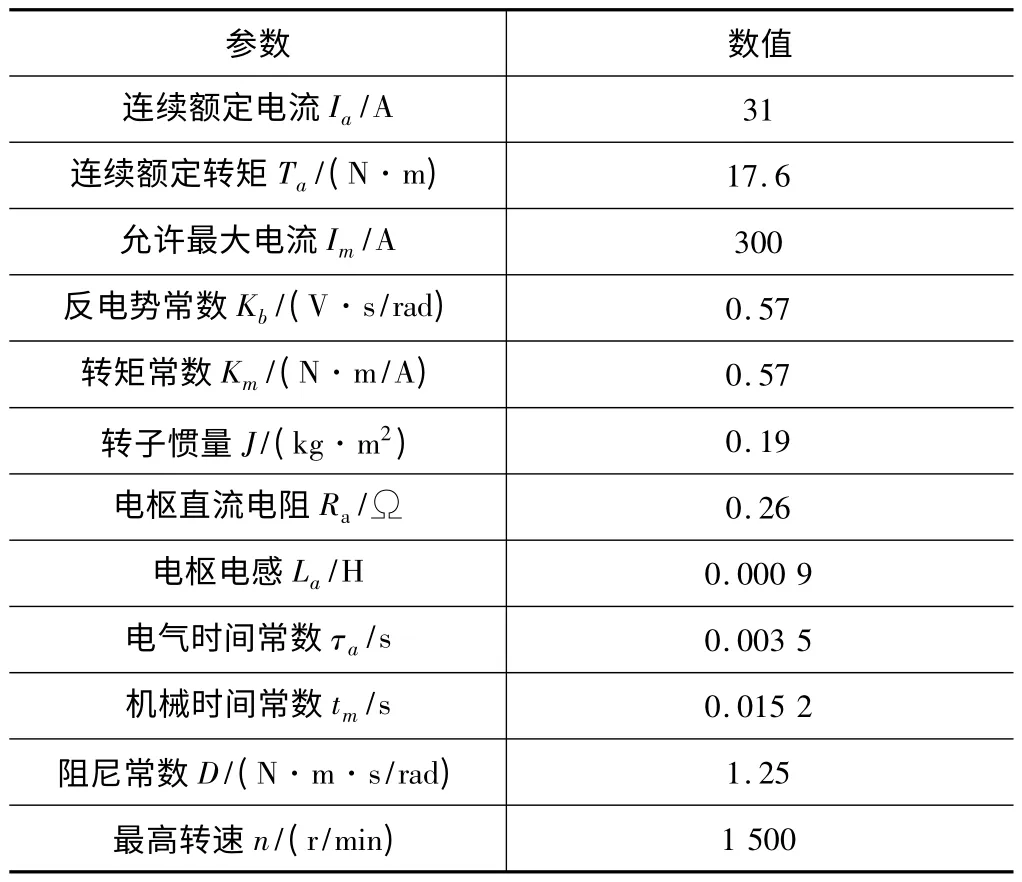
表1 FB-15 型直流伺服电动机数据

2.2 初步整定参数仿真

在Simulink 中建立仿真模型，带入初步整定的调节器参数可获得三环时域响应和频域相应参数。

(1)电流环仿真结果

电流环超调量σ=4.83%，在电动机最大电流允许范围内。系统上升时间tr=0.009 56 s，调节时间ts=0.027 7 s，系统的稳态误差为0。电流环的幅值裕度Gm=4dB，相角裕度Pm=49.8°，经初步整定的电流环即达到稳定。

保持电流调节器积分时间常数τi不变，改变比例系数Ki，由绘制的电流环时域响应曲线可知，电流调节器的比例系数影响系统的快速性和稳定性。Ki越大，系统响应越快，同时系统超调量越大。

(2)速度环仿真结果

系统超调量σ=20.3%，偏大。系统上升时间tr=0.0315 s，调节时间，系统的稳态误差为0。获得速度环的幅值裕度Gm=7.5dB，相角裕度Pm=33.8°，速度环的抗干扰性能满足要求。

(3)位置环仿真结果

按照传统方法整定的位置调节器比例系数偏大，系统出现了超调，需手动调节，减小参数，使超调量减为0。位置环幅值裕度也较小，但满足系统稳定要求。

3 遗传算法设计及求解

3.1 染色体编码

为使计算过程调试更为直观，采用实数编码方式，取Size=30 个样本进行编码。依手动调节获得的经验值，电流调节器比例系数Kip的取值范围为［0，0.005］，电流调节器积分常数Kii取值范围为［0，3］，速度调节器比例系数Knp的取值范围为［0，8］，速度调节器积分常数Kni取值范围为［0，0.1］，位置调节器比例系数取值范围为［0，10］。

将两变量在其各自定义域上离散化为Size 个实数，获得两条初始染色体编码序列Kpid为

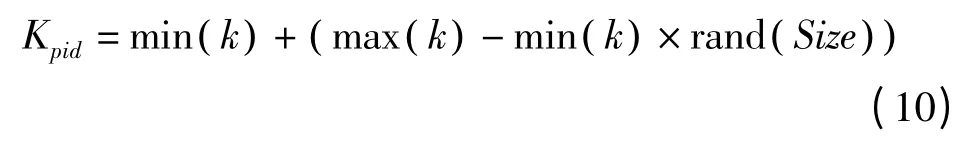
3.2 种群初始化及适应度函数计算

采用了随机初始化方法进行种群初始化。编写了优化目标函数程序和遗传算法参数整定程序。在程序执行过程中，为获取满意的过渡过程动态特性，采用误差绝对值时间积分性能指标作为参数选择的最小目标函数。为防止控制能量过大，在目标函数中加入控制输入的平方项。选用下式作为参数选取的最优指标:

式中:e(t)为系统误差;u(t)为控制器输出;tu为上升时间;W1、W2、W3为权值。在多目标优化问题中，权值代表各子目标在多目标优化问题中的重要程度。通过权值系数将各子目标函数线性加权，从而使多目标优化问题转化为单目标优化问题，即可以利用单目标优化的遗传算法求解多目标优化问题。

本文采用了几种不同的优化目标函数，作为参数选择的最小目标函数J，并取个体适应度函数F=1/J。

3.3 选择算子

选择运算使用比例算子。比例选择因子是利用与个体适应度大小成比例的概率决定其子孙的遗传可能性。个体被选中的概率为:

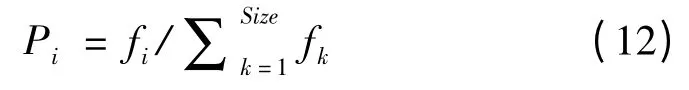
如果个体的选择概率大，则它的遗传基因就会在种群中扩大;如果个体的选择概率小，则被淘汰。

3.4 交叉操作

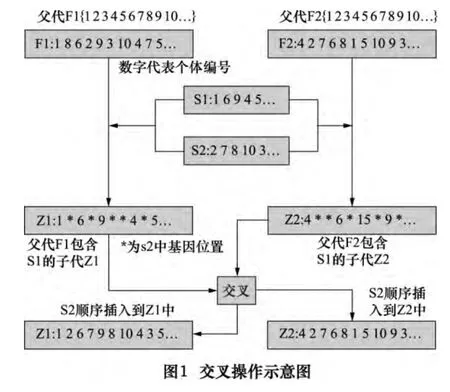
交叉操作决定遗传算法的全局搜索能力。采用单点交叉运算，过程如图1 所示。

任意挑选经过选择操作后种群中的两个个体作为交叉对象，随机产生一个交叉点位置。两个个体在交叉点位置互换部分基因代码，形成两个子个体。

3.5 变异操作

按照个体的适应度进行变异评估。适应度越大，变异概率越小。将被选择变异位置基因座上的值变异为在目标值定义域内的其它随机值。

4 计算结果分析对比

4.1 电流环仿真结果分析

经过100 代进化获得的优化参数Kip=0.004 1，Kii=0.958 2，τi=0.004 28，最佳性能指标值J=6.833 4。目标函数J 的优化过程和采用整定PID 参数的系统时域、频域响应曲线如图2、3、4 所示。

与初次整定仿真结果对比见表2。

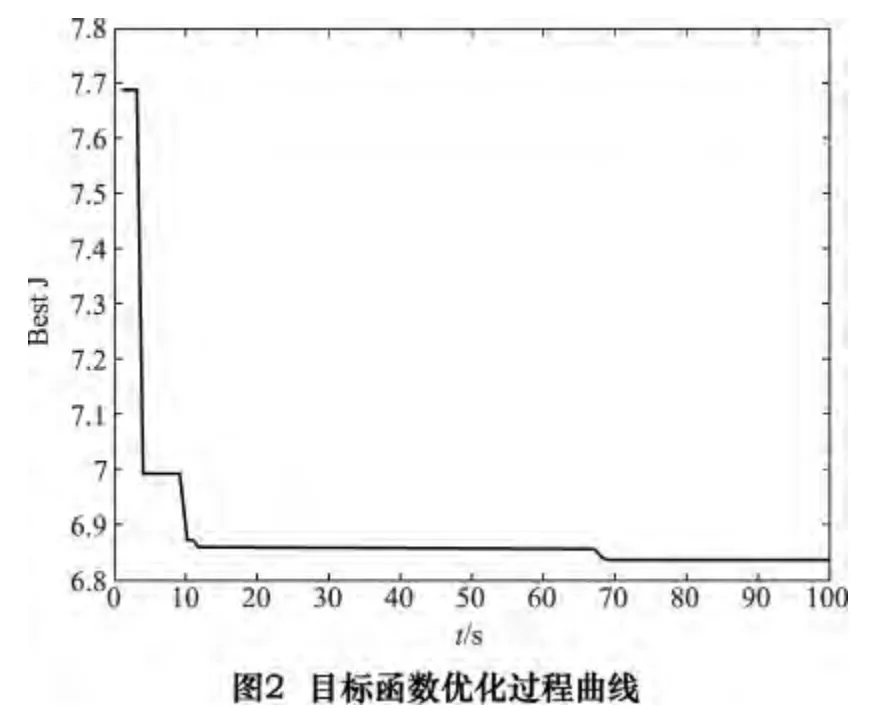
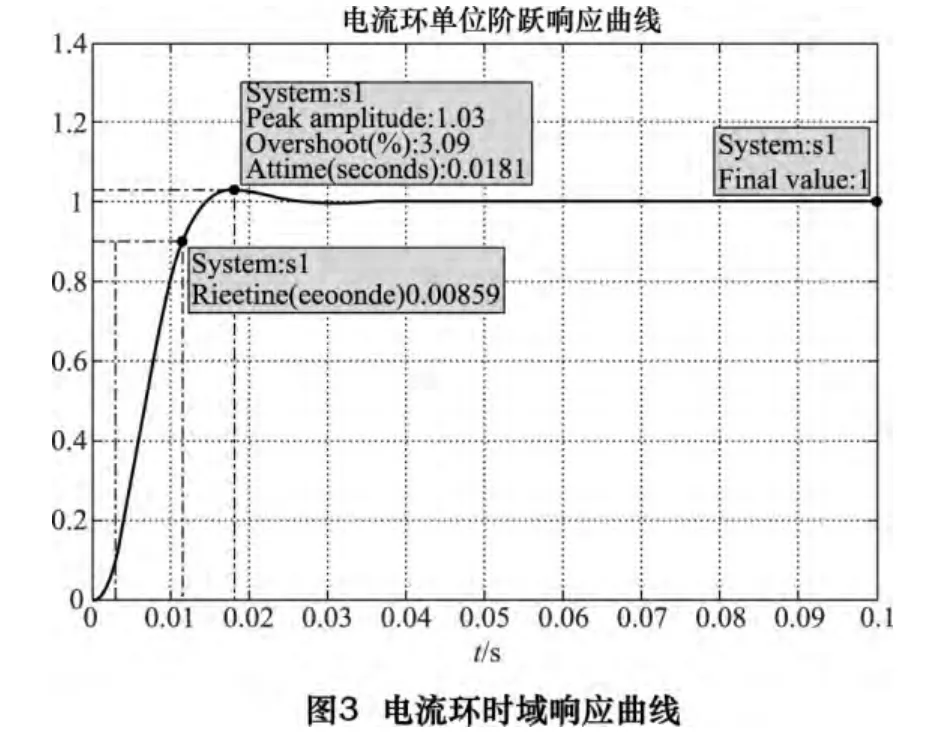
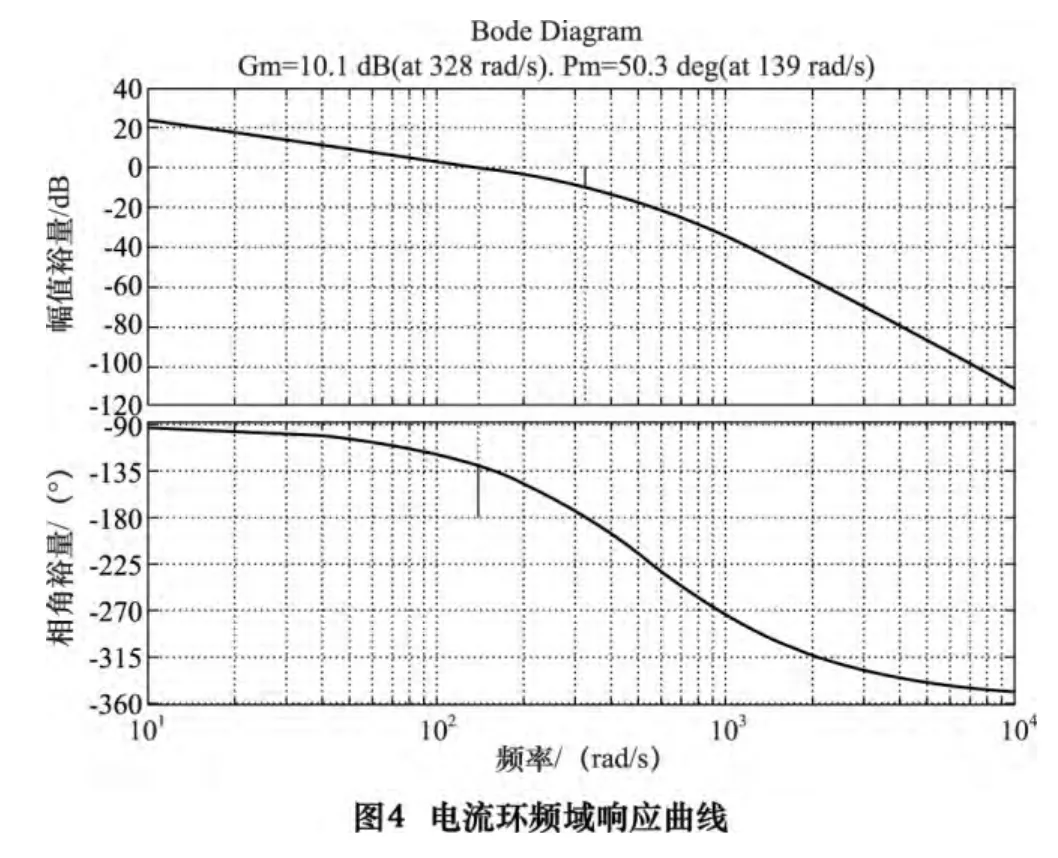
对比表2 数据不难得出结论，经遗传算法整定的电流环超调量减小，响应速度变快，频域稳定性也增强。该结果足以显示本文采取的PID 参数整定方法的有效性。

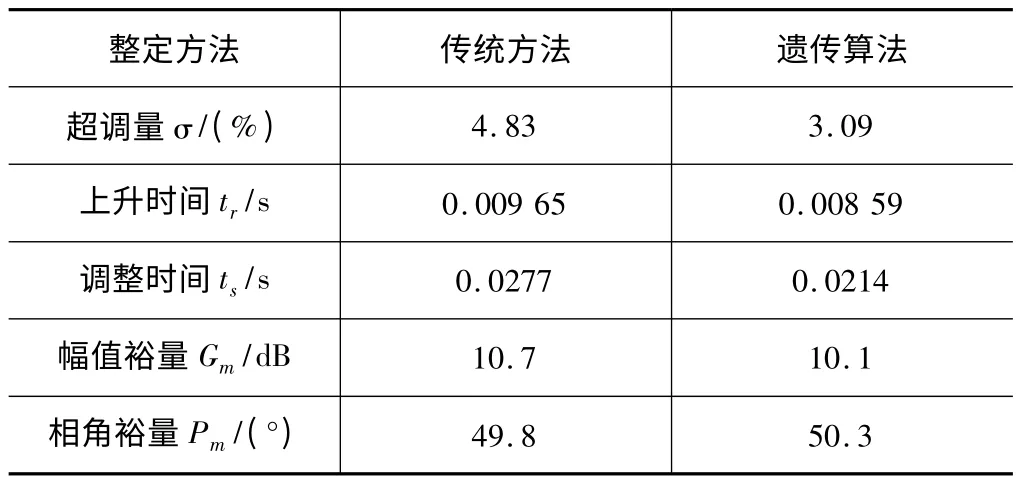
表2 电流环仿真结果对比

4.2 三环参数整体寻优结果分析

为使电动机在启动与制动阶段有足够大的转矩，加快电动机运动加速度，一般厂家都会对自己产品的电流环参数进行出厂设置，故整体优化环节中不对电流环参数进行优化，选用前一节整定后的电流调节器参数。

针对整体系统对位置环控制参数寻优。为避免超调，采用了惩罚功能，即一旦产生超调，将超调量作为最优指标的一项，此时最优指标为:

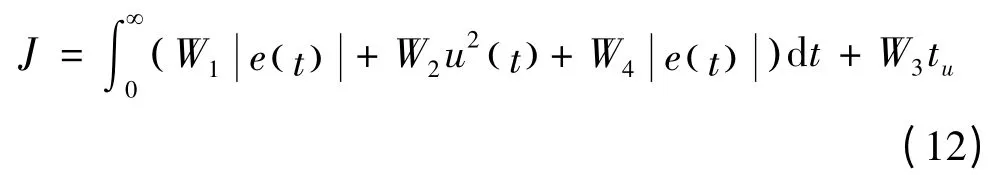
式中:W4为权值，且W4≫W1。

经计算获得的优化参数速度环比例系数Knp=4.804，速度环积分数Kni=0.008，位置环比例系数Ksp=9.242。绘制系统位置环单位阶跃响应曲线如图5所示。获得的系统主要性能指标对比见表3。

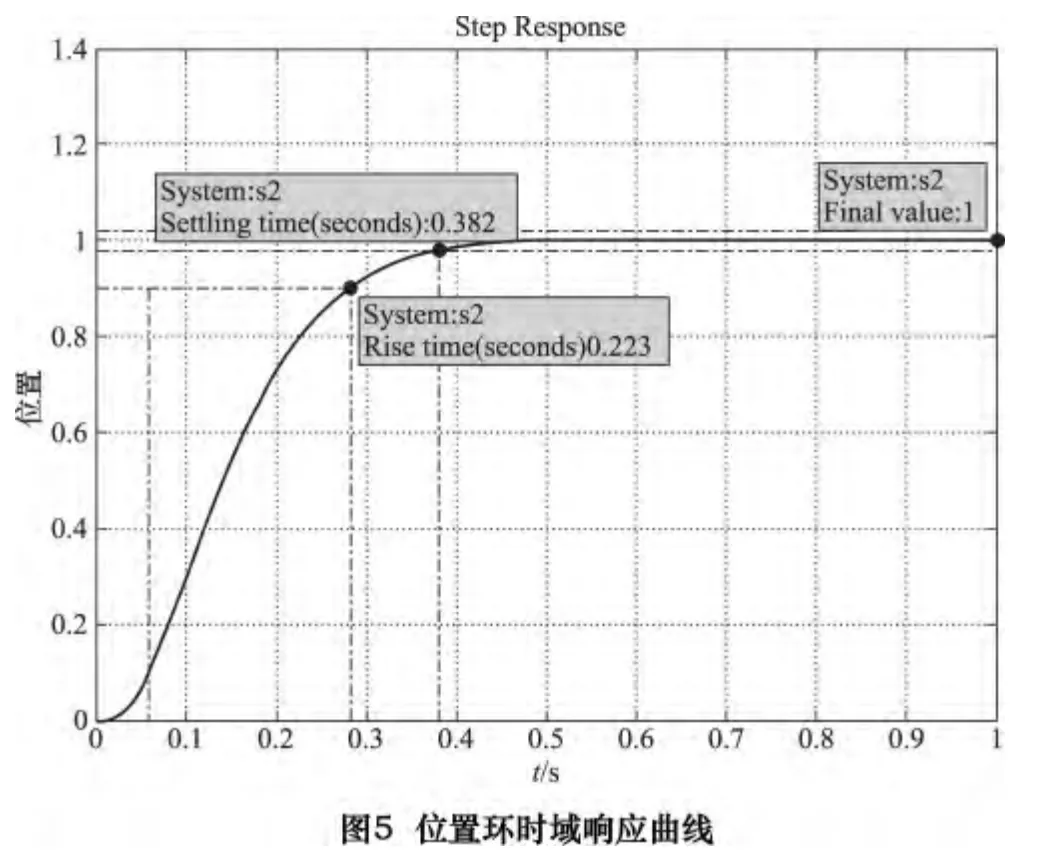
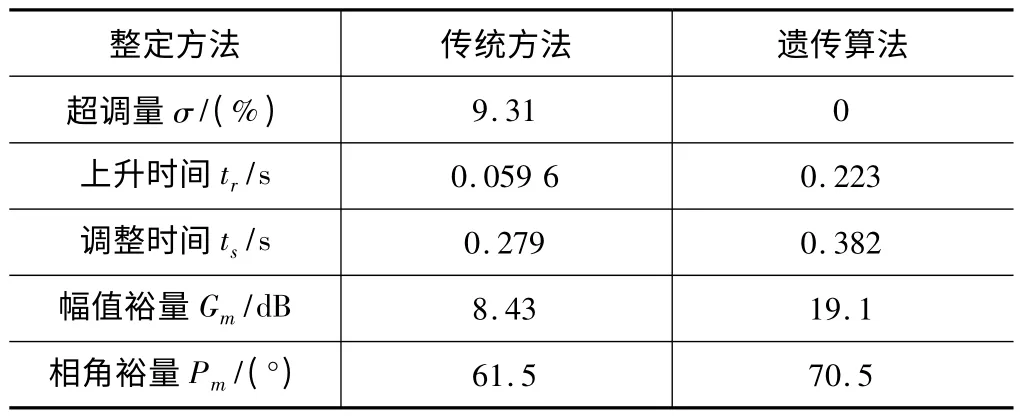
表3 三环整体优化仿真结果对比

经遗传算法优化的位置环仿真结果满足了位置环无超调的要求。上升时间减慢不少，但调整时间延迟不大，并且获得了较大的幅值裕量和相角裕量，证明了利用遗传算法优化后的系统稳定性提高。该结果证明了遗传算法用于PID 控制器参数整定的可行性和有效性。

4.3 关于优化目标函数的选择

现代控制理论假设系统工程师以量化的形式提出期望的性能指标。利用遗传算法对伺服系统的调节器参数进行优化时，目标函数是对系统的综合性评价，它是控制系统预想输出值与实际输出值之差的某个函数的积分。对目标函数的选择，能直接影响到伺服系统的动态响应和稳态精度，所以目标函数既要能反映系统的特性，又要方便计算。

几种常用的目标函数有以下几种:

代入不同目标函数获得的仿真结果见表4。

在优化中，采用ISE 和IAE 准则，没有引入积分时间的参量，对各个时刻误差是平等对待的。因此，优化变量将使系统的单位阶跃响应在最短时间内达到目标值，会造成很大的超调，因此在这两种方法的基础上引入时间环节加大后期误差的权重，将使系统的单位阶跃响应超调小，即为ITSE 和ITAE。用ITAE 优化的系统具有快速、平稳、超调小的特性。

而本文使用的目标函数不但考虑误差和时间，而且考虑到控制器输出以及超调惩罚因素。虽响应速度变慢，但系统可达到无超调的要求，且具有较大的幅值裕度和相角裕度，即系统抗干扰能力较强。对比以上因素，可见本文采用了较适当的目标函数。

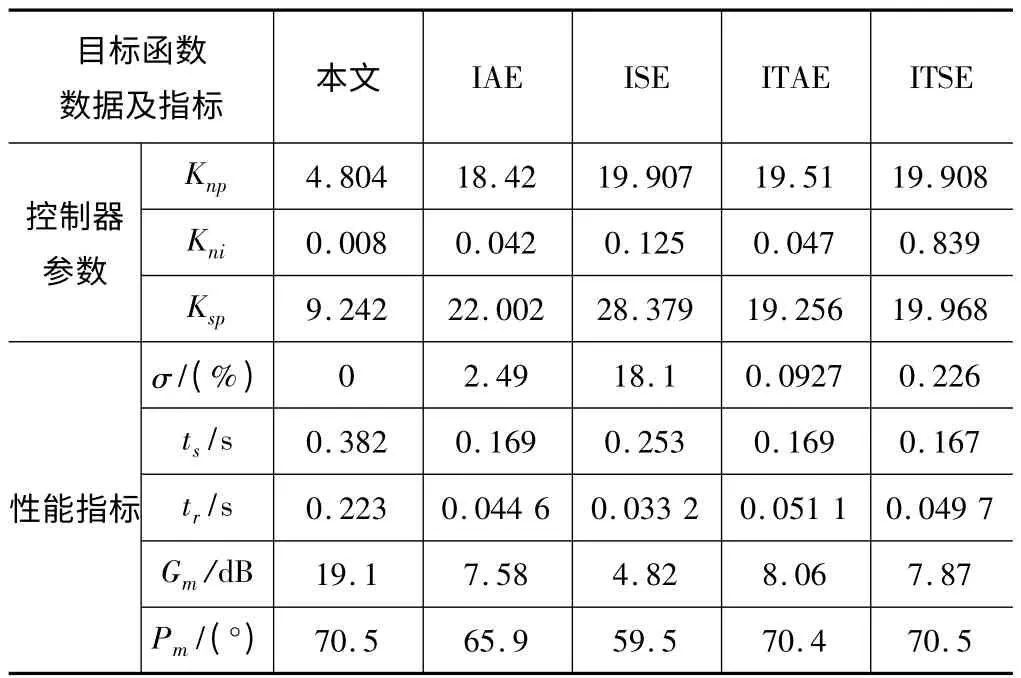
表4 常用目标函数优化结果对比

故决定遗传算法的目标函数时，要综合考虑系统的重要参数，权衡比重。可通过多次仿真实验确定最优目标函数。

5 实际系统测试

基于配有半闭环伺服系统的立式数控铣床进行试验。实验中使用了KH2000 稳压电源，SC -10 型光线示波器，HP 双频激光干涉仪，SONYA -69 磁带记录仪，Y6D-2 三通道动态电阻应变仪，位移传感器。实验装置原理见图6。

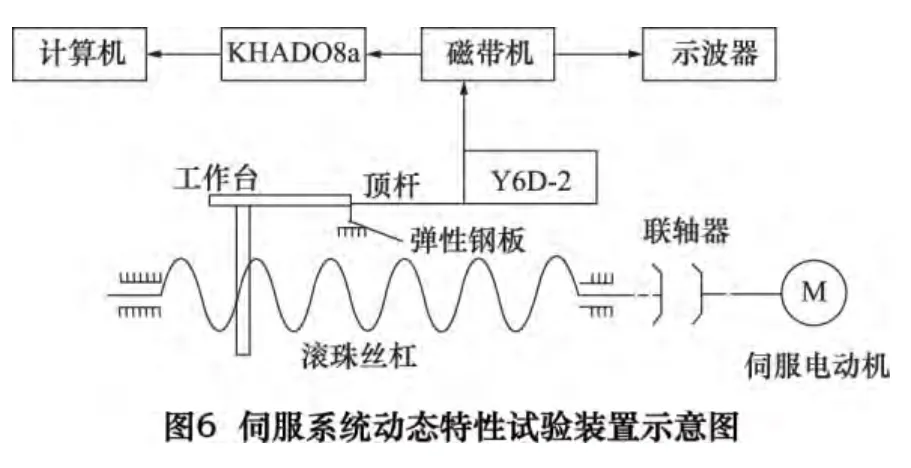
在加工中心X 向工作台上安装位移测量装置。在工作台一端安装顶杆，在导轨与床身上安装一个弹性良好的钢板，其根部贴电阻应变片，在床身上贴温度补偿片。控制钢板变形(即控制工作台行程)在弹性范围内。用高精度双频激光干涉仪进行标定，从而间接地测量到工作台的实际位置变化。为了排除或减少其他噪声的影响，顶杆和弹性钢板有一定的预压紧量。启动CNC 系统，依照所需工况调节参数，再使工作台加速运动，则钢板发生变形，应变片将应变信号送入动态电阻应变仪并转化为电信号，再将输出信号送入磁带记录仪记录下来。

系统X 轴及Z 轴的实验结果与仿真结果基本吻合。Y 轴滑座由于负有重约1 t 的X 向工作台，位置环超调量达17%，并容易引起震荡。此结果表明，工作载荷变化对系统特性有着重要影响，重载情况下参数设定需考虑载荷干扰。

6 结语

本文提出了用遗传算法整定直流伺服系统PID 参数的方法。利用Matlab 编写遗传算法程序，并通过Simulink 仿真获得系统响应参数。仿真及试验证明，利用遗传算法进行PID 参数整体优化，可以获得满足系统要求且使系统较为稳定的优化结果。选取遗传算法的目标函数，要综合考虑系统对误差、时间等参数的要求。可以通过加入权值的方法调节各因素在目标函数中的比重。

［1］刘金琨.先进PID 控制MATLAB 仿真［M］.3 版.北京:电子工业出版社，2011.

［2］阮毅，陈伯时.电力拖动自动控制系统:运动控制系统［M］.北京:机械工业出版社，2010.

［3］薛定宇.控制系统计算机辅助设计及:MATLAB 语言与应用［M］.北京:清华大学出版社，2006:167 -170.

［4］范晋伟，刘栋，杨磊，等.数控机床伺服系统动态特性的理论分析与仿真研究［J］.液压与机床，2008，36(2):159 -162.

［5］曹美宁.数控机床伺服进给系统动态响应仿真及其负载特性的研究［D］.北京:北京工业大学，2004.