一道调研题引起的研究
●姜卫东 戚有建(扬州中学江苏扬州225009)
一道调研题引起的研究
●姜卫东 戚有建(扬州中学江苏扬州225009)
很多高考题、模考题、调研题看起来很平常,实际上却丰富多彩,是命题专家经过精心思考命制出来的,有很大的研究空间和教学价值.本文从一道期末调研题出发,首先研究问题的不同解法,然后将问题推广为一般情况,最后揭示问题的深刻背景.
1 考题展示
例1已知椭圆的中心在坐标原点,左焦点为F1(-1,0),右准线方程为x=4.
1)求椭圆的标准方程.
2)若椭圆上动点N到定点M(m,0)(其中0<m<2)距离的最小值为1,求m的值.

图1
3)分别过椭圆的4个顶点作坐标轴的垂线,围成如图1所示的矩形,A,B是矩形的2个顶点.P,Q是椭圆上2个动点,直线OP,OQ与椭圆的另一交点分别为P1,Q1,且直线OP,OQ的斜率之积等于直线OA,OB的斜率之积,试探求四边形PQP1Q1的面积是否为定值.
答案1);2)m=1;3)面积为定值
点评本题是江苏省扬州市2015年1月高二期末调研试题的第19题,即试卷的倒数第2题,是该卷的选拔题,考查了椭圆的方程和性质、椭圆中的最值问题、椭圆中的定值问题.第1)小题学生很容易上手,用待定系数法求出基本量a,b即可;第2)小题用函数思想转化为二次函数的最值问题来处理,但要注意隐含的定义域,实际上这是由椭圆的范围(有界性)引起的;第3)小题用解析法来处理,有一定难度和区分度,也有很大的研究空间.在这里,笔者重点研究第3)小题.
2 解法探究
解法1(以k为参数)设直线OP的方程为y=kx,代入,整理得

点评解法1以直线OP的斜率k为参数,解出点P,Q的坐标,然后求|OP|及d,从而求面积.由于解题过程中仅涉及一个参数k,因此思路清晰,目标集中,学生容易把握.要注意的是,在求△OPQ的面积时,要合理选择底边,阅卷时发现很多学生选PQ为底边,导致计算繁杂,很难进展下去.实际上,以OP为底边要比以PQ为底边简单得多.
解法2(以k,b为参数)当直线PQ⊥x轴时,易得


点评解法2以直线PO的斜率k和截距b为参数,不需要解出点P,Q的坐标,借助韦达定理求|PQ|,从而求面积.此解法通俗易懂,学生容易想到,但是由于解题过程中涉及2个参数k,b,因此消参时有一定困难,对学生的运算要求较高.
解法3(以x1,y1,x2,y2为参数)设P(x1, y1),Q(x2,y2),则由,得

点评解法3以点P,Q的坐标x1,y1,x2,y2为参数,通过代数运算(坐标运算)来解决几何问题(面积问题),设而不求,充分体现了解析几何的基本思想.但由于解题过程中涉及4个参数x1,y1,x2,y2,因此消参时有一定困难,对代数变形的要求较高.
另外,解法3中在求S△OPQ时也可以用公式来处理,过程如下:
可以看出(图1),淮海经济区各城市旅游经济与城镇化的耦合度呈现非均衡的空间格局,耦合度值从0.258到1.000分布不等.3个年份最低的分别为枣庄、蚌埠和商丘,最高的分别为济宁(2005,2010年)和临沂,说明其分布极不稳定.淮海经济区3年的耦合度均值分别为0.926,0.898和0.947,表明淮海经济区旅游经济和城镇化复合系统整体上还处于高水平阶段.省域对比来看,耦合度由高到低分别为豫东、鲁南、苏北和皖北地区.

解法4(以α,β为参数)设,则由,得

点评解法4实际上是联想到椭圆的参数方程进行三角换元,以α,β为参数,将问题转化为2个三角式来处理,解法优美,过程简洁.回顾以上4种解法,方法迥异又有异曲同工之处,求解过程中都经历了“引参、用参、消参”三步曲.
3 推广研究
结论分别过椭圆(其中a>b>0)的4个顶点作坐标轴的垂线,围成如图1所示的矩形,A,B是所围成的矩形在x轴上方的2个顶点,P,Q是椭圆上2个动点,直线OP,OQ与椭圆的另一交点分别为P1,Q1.若直线OP,OQ的斜率之积等于直线OA,OB的斜率之积,则四边形PQP1Q1的面积为定值2ab.
证明过程类似,从略.
4 背景研究
实际上,单位圆x2+y2=1通过变换T:可以化为椭圆,该变换具有如下性质:
性质1直线在变换后,得到的仍然是直线,并且垂直于坐标轴的直线变换后仍垂直于坐标轴,不垂直于坐标轴的直线的斜率变为原来的倍.
性质2在变换前后对应线段的长度之比不变.
性质3若直线和圆相切(相交、相离),则变换后直线和椭圆相切(相交、相离).
用上面的伸缩变换知识来解释本题过程如下:因为在变换后的椭圆中,根据上面的性质1可得,在变化前的单位圆中“kOPkOQ=-1”,从而OP⊥OQ,因此四边形PQP1Q1为正方形,故S正方形PQP1Q1=2.再根据上面的性质4可得,变换后椭圆中的S四边形PQP1Q1=2ab.原来如此!
5 背景应用
笔者做了一些研究,发现很多高考题都与伸缩变换有关,有些试题利用伸缩变换可以得到简洁解,有些试题就是通过伸缩变换命制出来的.
例2如图2,在平面直角坐标系xOy中,M,N分别是椭圆的左顶点、下顶点,过坐标原点O的直线交椭圆于点P,A,其中点P在第一象限.过点P作x轴的垂线,垂足为C,联结AC,并延长交椭圆于点B,设直线PA的斜率为k.

图2
1)若直线PA平分线段MN,求k的值;
2)当k=2时,求点P到直线AB的距离d;
3)对任意的k>0,求证:PA⊥PB.
(2011年江苏省数学高考试题第18题)
答案1)2)3)略.
点评对于第3)小题,标准答案给出了2种解法,但运算量都较大,许多考生都因运算繁杂没能做到底.实际上,借助伸缩变换,能得到简洁的证法.由圆的几何性质及伸缩变换的性质可得

这种解法不仅简洁,而且更能看出椭圆与圆的紧密联系!
例3如图3,已知点A(0,-2),椭圆(其中a>b>0)的离心率为,F是椭圆的焦点,直线AF的斜率为,O为坐标原点.
1)求椭圆的方程;
2)设过点A的直线l与椭圆相交于点P,Q,当△OPQ的面积最大时,求l的方程.
(2014年全国数学高考新课标卷第20题)
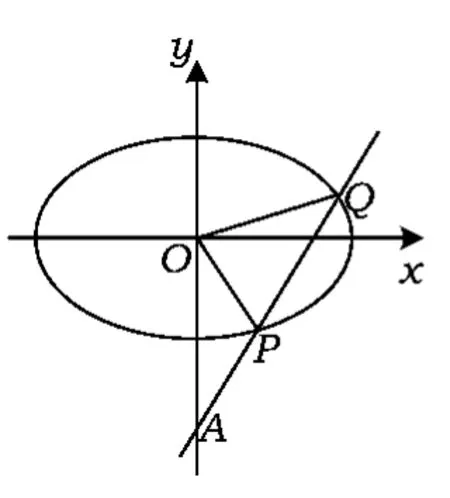
图3

图4
答案1);2)
点评先通过伸缩变换化归为有关圆的问题,就是这样一道题:
如图4,过点A(0,-2)的直线l与圆x2+y2= 1相交于点P,Q,当△OPQ的面积最大时,求l的方程.
此时非常简单,由于

故当∠POQ=90°时,
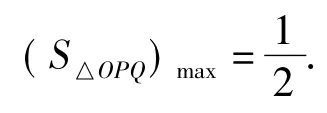
6 反思感悟
利用伸缩变换将圆与椭圆进行互化,通过圆的问题产生椭圆的问题,将椭圆的问题化归为圆的问题来解决,这实际上正是关系映射反演方法的一个具体应用,其中的关系可用图5表示:
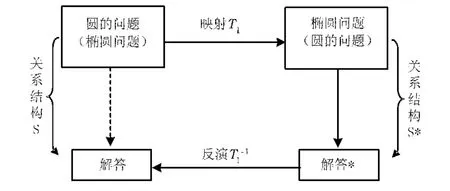
图5

