一类弱非线性互补问题的模系矩阵多分裂迭代算法

夏泽晨，李郴良

(桂林电子科技大学 数学与计算科学学院，广西 桂林541004)

互补问题在力学、工程、经济、交通等研究领域有着广泛的应用，如力学中的接触问题、弹塑性问题，工程中的障碍和自由边界问题、流体弹性动态润滑问题、最优控制问题、交通平衡问题以及经济均衡问题等，均可归结为互补问题。关于互补问题的研究一直是计算科学的热点问题，受到众多专家学者的关注。

关于用迭代法求解线性互补问题，Bai Zhongzhi［1］提出了一类模系分裂迭代算法，该算法通过将线性互补问题变换为一类与它等价的不动点方程组进行迭代计算。在此基础上，Bai Zhongzhi等［2］提出了模系矩阵多分裂迭代算法，该算法显示出较好的计算效果。张丽丽［3］总结了关于互补问题的模系矩阵分裂迭代算法，介绍该系列算法的一个通用框架以及一系列的模系松弛迭代方法。Li Chenliang等［4］提出了多重Schwarz算法，将多重分裂算法的求解范围扩大到了对角凸非线性互补问题，并推广了该类方法的适用范围。

本研究主要考虑一类弱非线性互补问题［5］的快速算法。Noor［5］通过变量变换把这类互补问题转化为一类与之等价的不动点方程组，并讨论有关这类弱非线性互补问题的算法。本研究将模系矩阵多分裂迭代算法推广到求解这类弱非线性互补问题，提出一种新的求解方法。

1 预备知识

弱非线性互补问题:

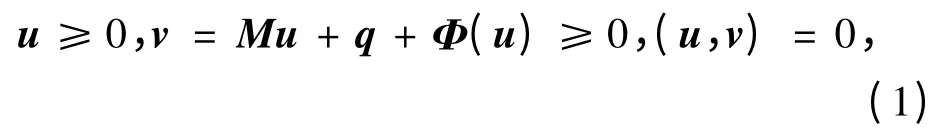
其中矩阵M∈Rn×n，向量q∈Rn，非线性项Φ(u)满 足Φ(u)=(α1(u1)，α2(u2)，…，αn(un))T，αi(ui)为一个定义域在实数上的实函数。

定义矩阵A=(aij)m×n，B=(bij)m×n∈Rm×n。设A≥B(A＞B)，有且仅有aij≥bij(aij＞bij)满足所有的1≤i≤m，1≤j≤n。若0为一个零矩阵且满足A≥0(A＞0)，则A为非负矩阵。定义为非负矩阵，且其元素为

令A∈Rn×n为一个实n阶矩阵，其比较矩阵

若其非对角元素是非正的并且其逆矩阵A－1≥0，矩阵A称为一个M-矩阵;若M-矩阵A的比较矩阵〈A〉也是一个M-矩阵，则矩阵A被称作一个H-矩阵;若其对角矩阵是正的，则H-矩阵A被称为H+-矩阵，若A为一个M-矩阵，Ω为一个正对角矩阵，当满足A≤B≤Ω时，则矩阵B为一个M-矩阵。

假设A=F－G，若F为一个非奇异的矩阵，则A=F－G被称为矩阵A的一个分裂;对于分裂A=F－G，若〈A〉=〈F〉－|G|，则这个分裂被称为H-相容分裂。若A=F－G为一个H-相容分裂，则有:

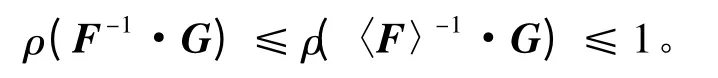
引理1［6］令A∈Rn×n为一个H-矩阵，D=diag(A)，B=D－A，则

1)矩阵A为非奇异;

2)|A－1|≤〈A〉－1;

引理2［7-8］(Perron-Frobenius定理)令A∈Rn×n为一个不可约非负矩阵，

1)ρ(A)为矩阵A的谱半径;

2)谱半径ρ(A)的特征向量x是一个正向量;

3)ρ(A)为矩阵A的一个特征值;

4)若矩阵A的任意一个元素增加，则ρ(A)增加。

利用相关概念，易证定理1。

定理1设M=F－G为矩阵M∈Rn×n的一个分裂，Ω为一个正对角阵，对于弱非线性互补问题(1)，以下结论成立:

1)若(u，v)为弱非线性互补问题(1)的一个解，则满足以下不动点方程组:

2)若x满足不动点方程组(2)，则有

这对向量(u，v)是弱非线性互补问题(1)的一个解。

2 模系多分裂迭代算法

在给出新的算法之前，引入如下矩阵多分裂概念。

定义1［7］设M∈Rn×n，l∈Z+且l≤n，若对于k=1，2，…，l，M=Fk－Gk为矩阵M的分裂，Ek∈Rn×n为非负对角矩阵，且满足则称(Mk，Nk，Ek)(k=1，2，…，l)为矩阵M的一个多分裂。

由定理1得到一个与弱非线性互补问题(1)等价的不动点方程组(2)，其中M=Fk－Gk，则有

由这个改进的式子可得以下迭代算法。

算法1

1)初始向量x(0)∈Rn，置m=0;

2)对于k=1，2，…，l，在对应的处理器上分别求解

3)再将l个处理器的求解结果组合在一起，得

若u(m+1)满足精度要求，则结束;若不满足，则转步骤2)继续计算。

3 收敛分析

定理2 已知M为一个H+-矩阵，D=diag(M)，B=M－D，正对角矩阵Ω≥D，非线性项Φ(u)=(α1(u1)，α2(u2)，…，αn(un))T，满足di＞。假设(Fk，Gk，Ek)(k=1，2，…，l;l≤n)为矩阵M的一个多分裂，且对于每个M=Fk－Gk为矩阵M的一个H-相容分裂，则对于任意初向量x(0)∈Rn，由算法1产生的迭代序列u(m{)收敛于弱非线性互补问题(1)的一个解u*。

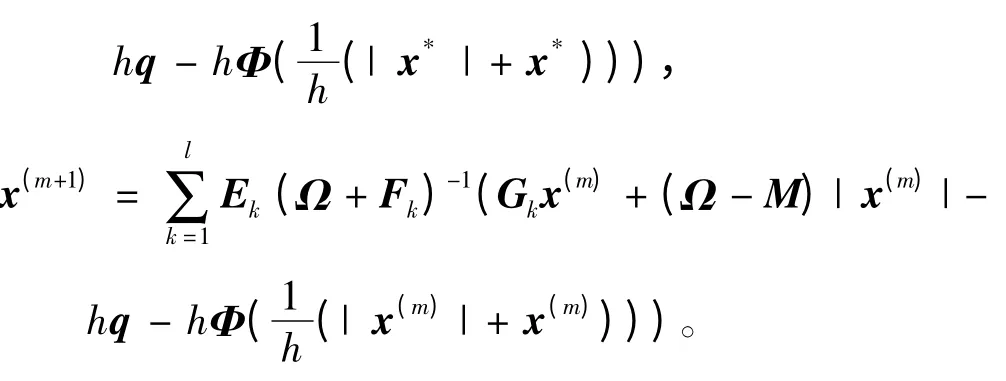
设x*是准确解，则有

于是，

因此，ρ(L)＜1，由算法1产生的迭代序列，收敛到弱非线性互补问题的一个解u*。

4 数值例子

实验在Matlab软件环境中模拟，终止条件为:

所有的初向量选择为x(0)=(0，0，…，0)T∈Rn。

例1［7］考虑弱非线性互补问题(1)，设矩阵M∈Rn×n为一个H+-矩阵，且为对角块矩阵，

矩阵B为一个三对角线矩阵

q=(1，－1，…，1，－1)T，为单位矩阵。

模系矩阵多分裂迭代法的实验结果如表1所示。m∈Z+满足n=m2，n为矩阵M的阶数;d为迭代步数;t为迭代时间。从实验结果可看出，模系多分裂迭代法的迭代速度快，迭代步数少，实验结果较理想。

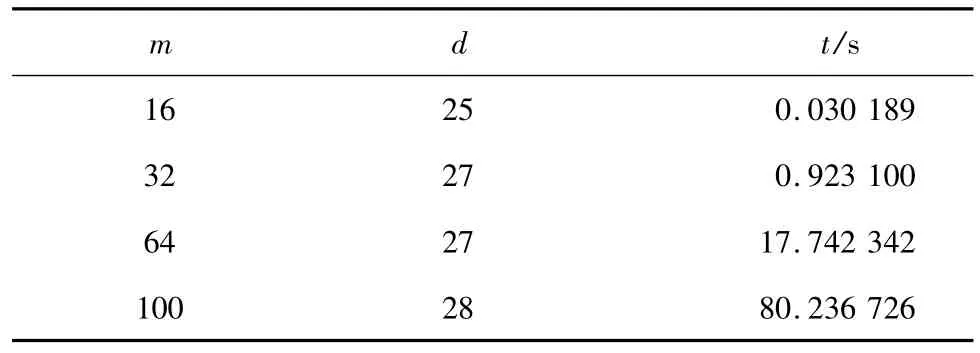
表1 模系矩阵多分裂迭代法的实验结果Tab.1 Experimental results of MSMGS iterative method

5 结束语

运用矩阵多重分裂理论，结合Bai Zhongzhi［1-2］提出的一类模系分裂迭代算法，给出了一类求解弱非线性互补问题的模系矩阵多分裂迭代算法，并分析了算法的收敛性。数值例子说明算法的有效性。

［1］Bai Zhongzhi.Modulus-based matrix splitting iteration methods for linear complementarity problems［J］.Numerical Linear Algebra with Applications，2009，17(6):917-933.

［2］Bai Zhongzhi，Zhang Lili.Modulus-based synchronous multisplitting iteration methods for linear complementarity problems［J］.Numerical Linear Algebra with Applications，2013，20(3):425-439.

［3］张丽丽.关于线性互补问题的模系矩阵分裂迭代方法［J］.计算数学，2012，34(4):373-386.

［4］Li Chenliang，Zeng Jinping.A mutisplitting and additive Schwarz iteration scheme for solving nonlinear complementarity problems［J］.Journal of Numerical Methods and Computer Applications，2003，24(4):268-275.

［5］Noor M A.Fixed point approach for complementarity problems［J］.Journal of Mathematical Analysis and Applications，1988，133(2):437-448.

［6］Bai Zhongzhi，Evans D J.Chaotic iterative methods for the linear complementarity problems［J］.Journal of Computational and Applied Mathematics，1998，96(2):127-138.

［7］Frommer A，Mayer G.On the theory and practice of multisplitting methods in parallel computation［J］.Computing，1992，49(1):63-74.

［8］Mangasarian O L.Solution of symmetric linear complementarity problems by iterative methods［J］.Journal of Optimization Theory and Applications，1977，22(4):465-485.