基于小波变换的新阈值函数语音去噪方法

刘继锦，周萍，杨青，景新幸

(1.桂林电子科技大学 电子工程与自动化学院，广西 桂林541004;2.桂林电子科技大学 信息与通信学院，广西 桂林541004)

语音识别广泛应用于民用和军用领域，由于语音信号含噪多，语音信号预处理不好容易造成语音识别错误，因此对语音信号的去噪极其重要。语音去噪的方法很多，传统上分为时域去噪和频域去噪。时域去噪方法有均值滤波法、加权平均法和中值滤波法等。频域去噪通过抑制或消除语音信息中的高频部分实现去噪。传统的去噪方法容易损害语音的边缘信息，使语音变得模糊。相对于传统去噪，小波变换［1］具有很好的时频局部特性，因此小波去噪得到了广泛的应用。基于小波变换的去噪法通常有模极大值去噪法、空域相关去噪法和小波阈值去噪法［2］等。其中小波阈值去噪法能达到很好的去噪效果，且易于实现，因此被大量应用。

小波阈值去噪效果的好坏，主要取决于阈值的确定和阈值函数的选取。阈值函数有硬阈值和软阈值［3］2种，但它们都有明显的不足，如:硬阈值函数不可摆脱的间断点问题，软阈值函数与生俱来的恒定偏差问题。这些不足造成了信号高频信息不完整、边缘模糊等，影响了去噪效果。硬阈值能保留语音细节，但易出现振荡和伪吉布斯效应等造成的语音失真［4］。软阈值处理语音较平滑，但易造成语音模糊，影响听觉效果。鉴于此，在解决以上缺陷的基础上构造了一种新的阈值函数，并提出了一种基于小波变换的新阈值函数语音去噪方法。

1 小波阈值去噪的基本原理

1.1 语音信号模型

语音信号通常由原始信号和噪声信号2部分组成。语音信号的模型为:

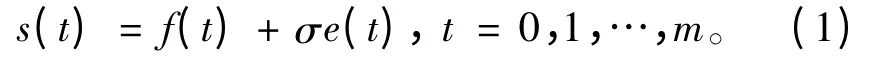
其中:s(t)为含噪语音信号;f(t)为原始信号;σ为噪声强度;e(t)为噪声信号。

1.2 阈值去噪的基本原理

语音信号经小波变换后，信号的能量集中在少数的小波系数上，而噪声点的小波系数互不相关，分布在各个尺度的所有时间轴上［5］，一般较小。相对而言，真实信号的小波系数比噪声的小波系数大很多，所以设定一个合适的阈值，过滤掉噪声系数，然后将处理后的系数逆变换，重构语音信号，便可达到去噪的目的。

1.3 阈值去噪步骤

1)信号分解。根据噪声的特点选择合适的小波基函数［6］，噪声的强弱决定分解层数的大小，从而确定最大分解尺度，然后对信号进行分解，经小波变换得到小波分解系数。

2)阈值处理。常见的阈值函数有硬阈值函数和软阈值函数［7］。硬阈值函数为:

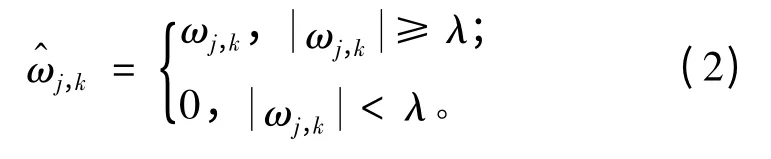
软阈值函数为:

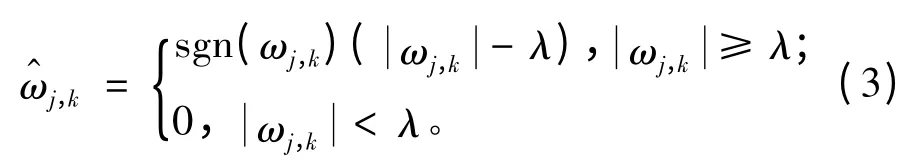
3)信号重构。根据未处理的小波低频系数和经阈值处理后得到的估计小波系数，进行小波逆变换，恢复信号［9］，从而达到去噪的目的。

2 新阈值去噪方法

硬阈值函数和软阈值函数虽然在实际中应用广泛，但也存在一些缺陷［10］。如硬阈值函数的阈值点有间断点，易使处理后的信号出现振荡和失真;软阈值函数的恒定偏差易造成信号高频信息不完整、边缘模糊等［11］。这些不足很大程度上影响了去噪效果，需对传统的阈值去噪方法进行改进，以达到更好的去噪效果。

2.1 改进阈值函数去噪方法一

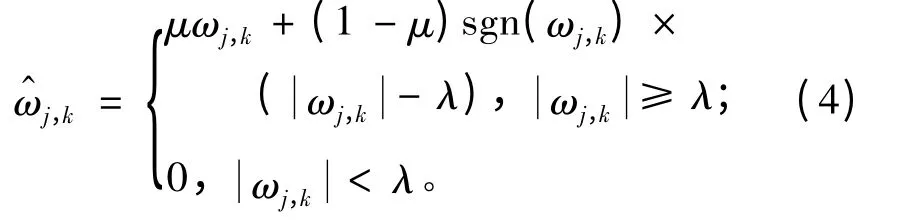
2.2 改进阈值函数去噪方法二

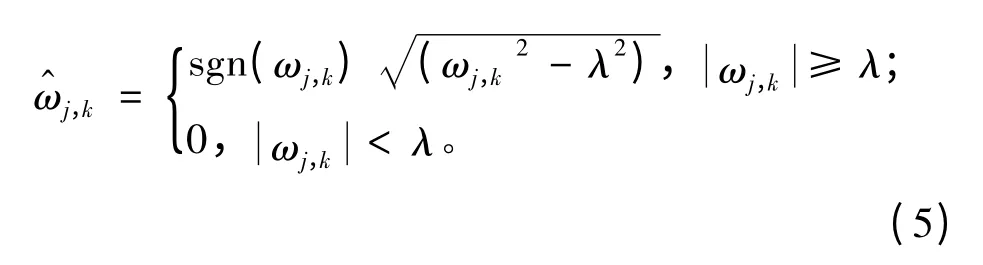
2.3 新阈值函数去噪

基于以上2种改进的阈值函数去噪方法，构造一种新的阈值函数，从数学角度对新阈值函数进行分析:

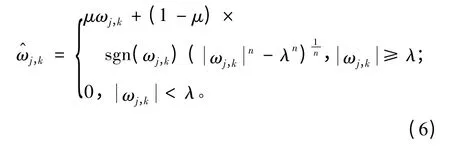
其中n为正整数。

2.3.1 函数的连续性

当ωj，k→λ－时，μ=0，

当ωj，k→－λ+时，μ=0，

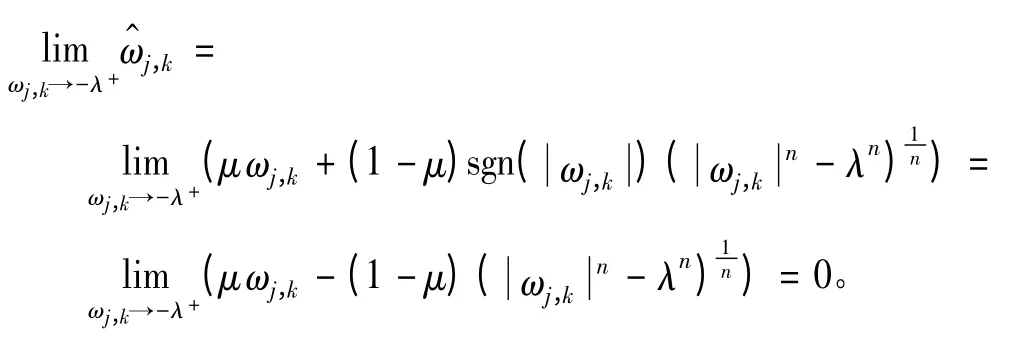
2.3.2 函数的偏差性

当ωj，k→∞时，μ=1，

因此，当ωj，k→∞时，与ωj，k相等，克服了它们之间存在的恒定偏差。

2.3.3 函数的渐近性

当ωj，k→∞时，由式(2)可得=ωj，k，因此，

2.3.4 函数的可导性

指数函数和幂函数都是高阶可导的，它们经过简单的四则混合运算后不影响其可导性。新阈值函数是由指数函数和幂函数经过简单的四则混合运算结合在一起的函数，因此具有高阶可导性。

2.3.5m、n对新阈值函数的作用

当m=∞，n取任意值时，新阈值函数变成了硬阈值函数;当m=0，n=1时，新阈值函数变成了软阈值函数。m和n的可变性使新阈值函数变得更加灵活。

3 实验结果及分析

为了验证新阈值函数去噪的优越性和有效性，分别采用传统的硬阈值函数、软阈值函数和新阈值函数进行仿真实验，用信噪比指标证明新阈值函数的优点。

信噪比是语音信号处理中描述去噪效果的重要指标［12］，其公式为:

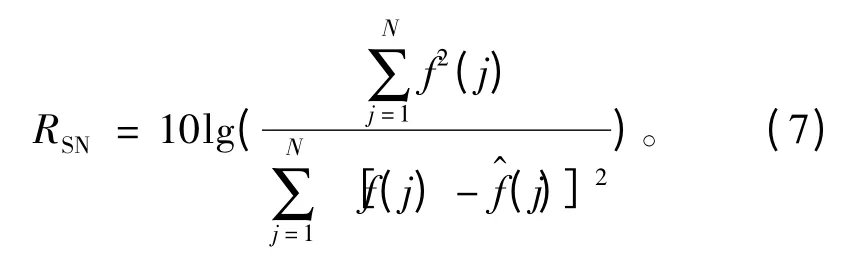
其中:f(j)为原始信号在取样点j的幅值j)为去噪后的信号在位置j的幅值;N为信号的长度。信噪比越高，则恢复后的信号越接近原始信号，去噪效果越明显。

为了检验新阈值函数的去噪效果，用Matlab 2010对原始blocks信号加入高斯白噪声进行去噪，分别采用硬阈值函数、软阈值函数及构造的新阈值函数方法进行去噪。blocks信号分别加入信噪比为5、10、15、20、25 dB的高斯白噪声。选择sym6为小波分析的小波基函数，分解层数为3，阈值输入信噪比为5 dB的3种阈值函数去噪方法处理后的信号如图1所示。从图1可看出，传统的硬阈值、软阈值函数及构造的新阈值函数方法基本都能复原原始信号，但硬阈值函数处理后的信号毛刺较多，有振荡导致的信号局部失真，软阈值函数处理后的信号虽然比较平滑，但降噪效果一般。与前2种去噪方法相比，新阈值函数处理后的信号毛刺少、失真小、振荡小，波形更平滑，能更大程度地接近原始信号，取得了满意的降噪效果。

输入信噪比分别为5、10、15、20、25 dB时，各阈值函数的输出信噪比如表1所示。

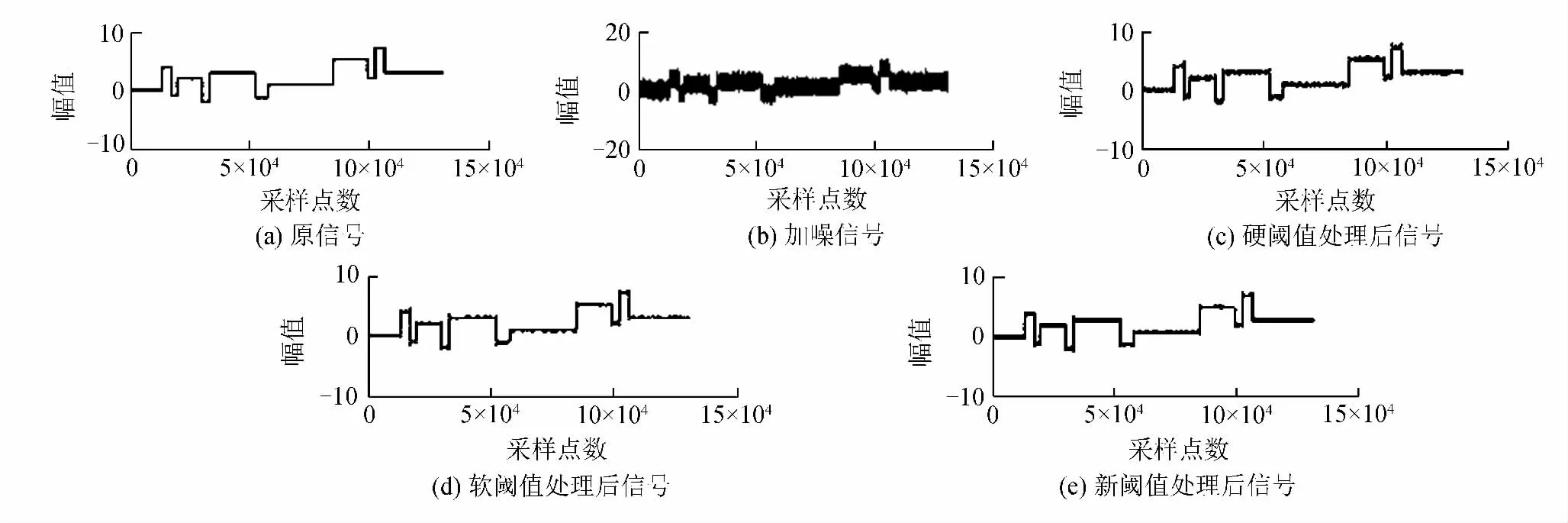
图1 输入信噪比为5 dB时的blocks信号Fig.1 The blocks signal when input SNR is 5 dB

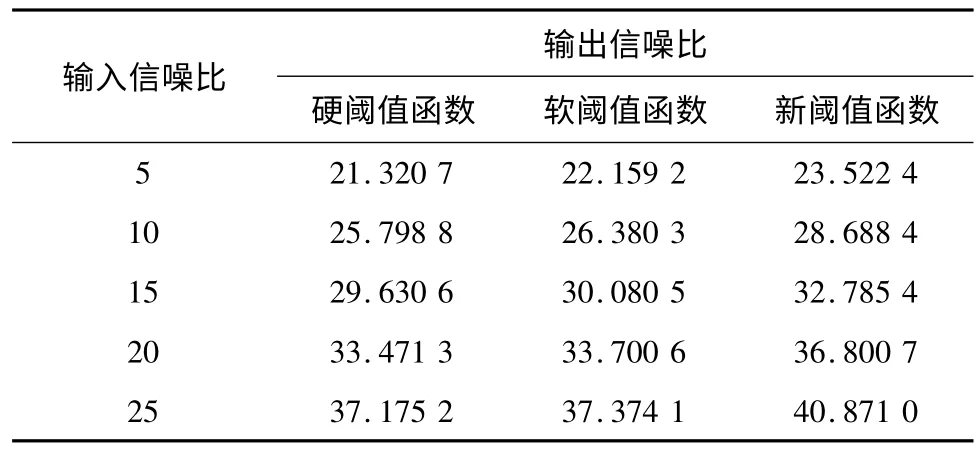
表1 阈值函数对blocks信号的去噪效果Tab.1 The denoising effect of threshold functions for blocks signal dB

从表1可看出，输入的信噪比越大，输出的信噪比也越大，相对去噪效果越明显，经新阈值函数处理后的降噪效果明显优于前2种函数，说明新阈值函数能更大程度地还原原始信号，更具参考性。

对blocks信号进行一系列加噪处理，在取得了良好效果的基础上，进一步对语音信号进行处理。用Matlab 2010通过3种阈值函数去噪方法对语音信号去噪，选取中文女生短句“于是大家结伴同行”作为去噪实验的纯净语音，噪声选取为高斯白噪声。纯净语音和噪声的采样频率均为8 kHz，分别加入信噪比为－5、0、5、10、15 dB的高斯白噪声，选择db9为小波分解的小波基函数，分解层数为4，阈值。输入信噪比为10 dB时，经各阈值函数处理后的语音信号如图2所示。

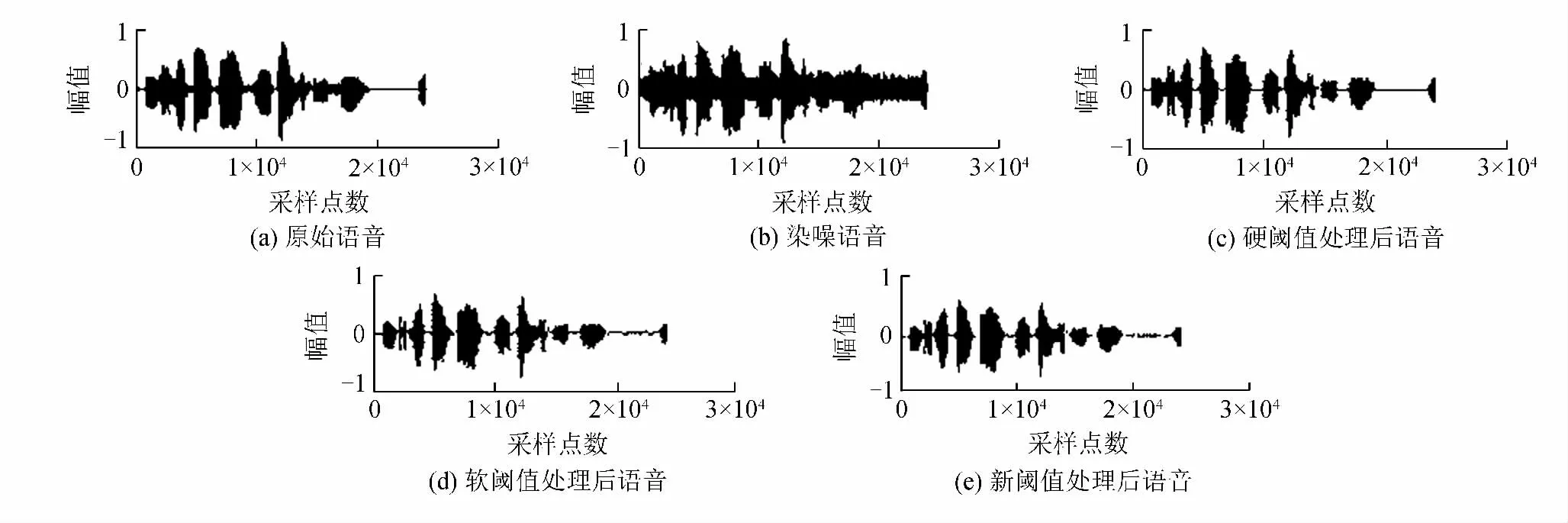
图2 输入信噪比为10 dB时的语音信号Fig.2 The speech signal when input SNR is 10 dB

从图2可看出，加噪语音经各种阈值函数处理后均能恢复原语音信号，但新阈值函数能更大程度地减少语音失真，更好地保留了语音信号的细节和真实信息，使听者更乐于接受，达到了期望的降噪效果。

由以上实验可看出，新阈值函数去噪法可有效地去噪白噪声干扰。在此基础上，对语音信号加入工厂噪声和汽车噪声，通过不同的噪声类型验证新阈值函数的去噪效果，其结果如表2所示。

从表2可看出，无论是对白噪声、工厂噪声还是汽车噪声，新阈值函数去噪法均取得了良好的去噪效果，从信噪比的角度更加客观地描述了新阈值函数去噪的有效性和优越性。

采用工厂里录制的真实语音，用8 kHz的采样率，单声道录音，量化精度为16 bit，提取每帧信号的24阶MFCC作为语音特征参数，用VQ(矢量量化)匹配算法对测试语音进行识别。在小波变换中，选用db小波阶数为9阶，小波分解层次为4层，语音分帧时，帧长采用128样值点。3种阈值函数的语音识别率如表3所示。

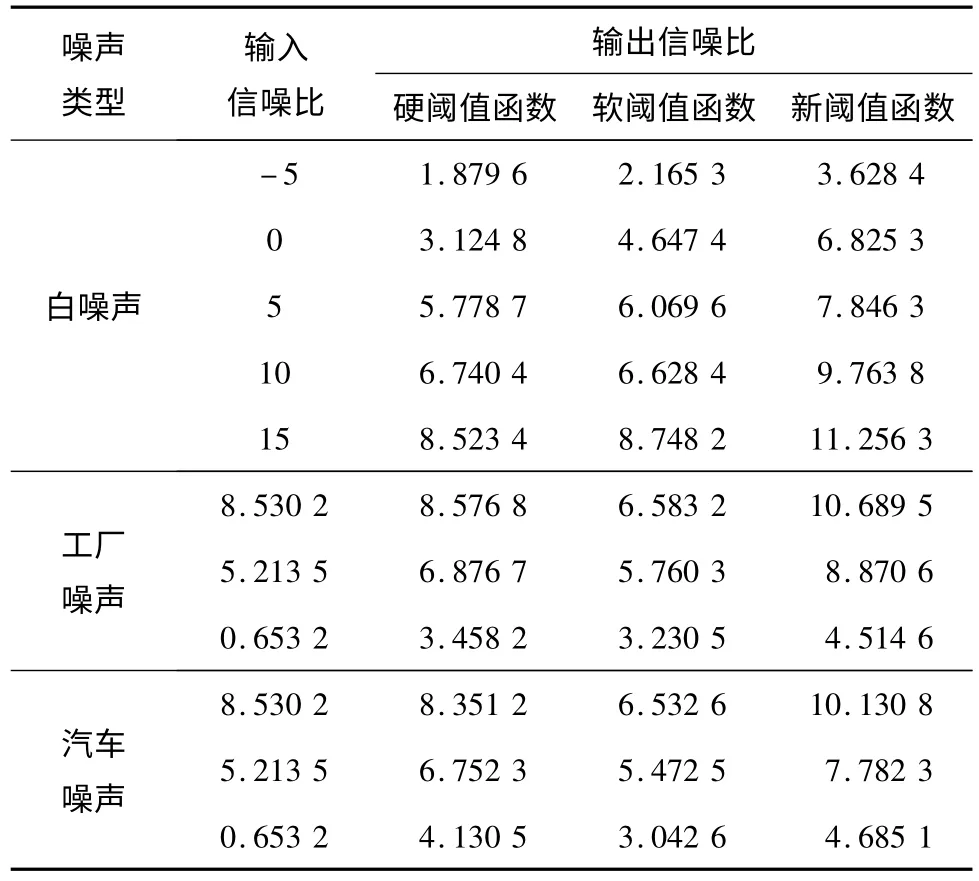
表2 不同噪声下3种阈值函数的输出信噪比Tab.2 Output SNR of three threshold functions in different noises dB

表3 3种阈值函数的语音识别率Tab.3 Speech recognition rate of three threshold functions %

从表3可看出，经新阈值函数去噪法去噪处理后，语音识别率明显提高。

4 结束语

小波阈值去噪法由于可有效去除噪声干扰，因而成为一种应用较为广泛的语音增强技术。由于阈值函数本身存在的问题，导致以往的阈值函数去噪法出现去噪不彻底或者去噪过度，使恢复后的语音出现偏差。为了解决上述问题，通过对传统阈值函数进行改进和构造，提出了一种基于小波变换的新阈值函数语音去噪方法。实验结果表明，该方法能达到去除噪声干扰的目的，解决了硬阈值函数的连续性问题和软阈值函数的恒定偏差问题，减少了语音失真，明显地改善了去噪效果，提高了语音识别率。

［1］李克粉，王直.改进的小波阈值去噪在语音识别中的应用［J］.计算机技术与发展，2013，23(5):231-234.

［2］齐翠丽.基于小波阈值法和模极大值法的语音去噪算法研究［D］.秦皇岛:燕山大学，2012:15-17.

［3］邓玉娟.基于小波变换的语音阈值去噪算法研究［D］.重庆:重庆大学，2009:23-25.

［4］杨鑫蕊.改进的小波阈值去噪算法研究［D］.哈尔滨:哈尔滨理工大学，2014:11-13.

［5］兰超，欧阳林子.一种基于改进的软硬阈值折衷法的去噪研究［J］.科学技术与工程，2009，9(18):5515-5517.

［6］叶重元，黄永东.小波阈值去噪算法的新改进［J］.计算机工程与应用，2011，47(12):141-146.

［7］周西峰，朱文文，郭前岗.基于渐近半软阈值函数的超声信号去噪方法［J］.探测与控制学报，2011，33(2):35-39.

［8］王卓，王庆生.基于改进小波阈值的倾角传感器去噪研究［J］.计算机测量与控制，2013，21(9):2607-2611.

［9］王蓓，张根耀，李智，等.基于新阈值函数的小波阈值去噪算法［J］.计算机应用，2014，34(5):1499-1502.

［10］任永梅，张雪英，贾海蓉.一种新阈值函数的小波包语音增强算法［J］.计算机应用研究，2013，30(1):114-117.

［11］代海波，单锐，王换鹏，等.基于改进阈值函数的小波去噪算法研究［J］.噪声与振动控制，2012，21(6):189-193.

［12］苑津莎，张冬雪，李中.基于改进阈值法的小波去噪算法研究［J］.华北电力大学学报，2010，37(5):93-95.