基于MBSBL-FMLM的宽带协作频谱感知算法

胡静，肖海林

(桂林电子科技大学 信息与通信学院，广西 桂林541004)

在认知无线电网络中，高采样率和无线信道衰落是宽带频谱感知的两大挑战，引入压缩感知技术可解决高采样率的问题［1-3］。文献［1-3］仅对单个次用户(second user，简称SU)宽带频谱感知的情况进行研究，而单个SU频谱感知无法克服无线通信过程中阴影衰落等不利因素的影响。为了减小无线信道衰落的不利影响，文献［4］研究了基于分布式压缩感知(distributed compressed sensing，简称DCS)的多个SU协作频谱感知情况，利用观测矩阵的自相关向量作为观测矩阵，获得了较好的检测性能，但自相关运算导致耗时较大。

在实际情况中，以合适的频率分辨率将宽带频谱按照子信道划分，主用户(primary user，简称PU)随机占用其中几个子信道，即PU信号的非零频点只集中几个子信道，为块稀疏结构［5］。文献［6］的研究表明，块稀疏结构可进一步降低采样率，并提高检测性能。而传统的基于DCS的联合重构算法(如SOMP算法［6］)并未考虑信号的块稀疏结构。文献［7］注意到了信号的块稀疏性和块内相关性，采用期望最大化(expectation maximization，简称EM)方法估计参数，获得了较好的重构效果，但算法收敛速度仍不够快，且只研究了单个SU参与频谱感知的情况。在此基础上，文献［8］提出多测量向量(multiple measurement vector，简称MMV)块稀疏贝叶斯学习(block sparse bayesian learning，简称BSBL)框架，简称MBSBL框架，利用快速边缘似然函数最大化(fast marginalized likelihood maximization，简称FMLM)方法估计参数，不仅得到了很好的重构效果，而且收敛速度明显提高。

采用基于DCS的多SU协作感知，考虑各个SU使用相同的种子产生伪随机±1序列，因而具有相同的观测矩阵Φ［9］，分布式压缩采样过程即可建模为MMV［10］问题。为提高宽带压缩频谱感知算法的准确性和有效性，提出了基于多测量向量块稀疏贝叶斯学习-快速边缘似然函数最大化(简称MBSBL-FMLM)的宽带协作频谱感知算法。

1 系统模型

图1所示为块稀疏信号的宽带协作频谱感知系统模型，若PU与L个SU共享某一带宽为W的频段，将其均分为P个窄带子信道，PU随机占用几个子信道，PU的发送信号为e(t)，第i(i=1，2，…，L)个SU接收信号的表达式为:

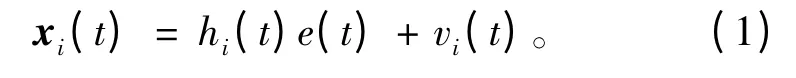
其中:hi(t)为PU与第i个SU之间的信道增益;vi(t)为无线信道的高斯白噪声。的频域形式为:

其中，ΨN为N×N维的傅里叶正变换基。各子信道信号频谱组合形式为:

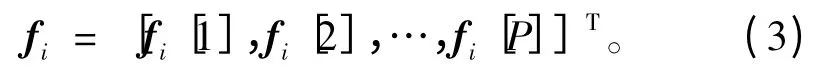
其中，各子信道的频谱长度为S=N/P，第p(p=1，2，…，P)个子信道的信号频谱为fi［p］=

在大部分频段，PU仅占用极少的子信道，大部分子信道处于空闲状态，所以信号频谱具有稀疏性［11］。根据压缩感知原理，若信号xi在频域下是稀疏的，可用一个与傅里叶正变换基ΨN不相关的观测矩阵Φ∈RM×N(M≪N)将xi投影到低维空间进行观测，并由观测数据重构信号频谱。

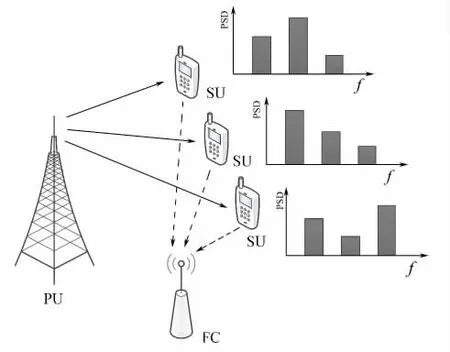
图1 块稀疏信号的宽带协作频谱感知模型Fig.1 Wideband cooperative spectrum sensing model of block sparse signal

采用模拟/信息转换器(analog-to-information conversion，简称AIC)对宽带信号xi进行压缩采样，xi的M×1维的观测序列为:

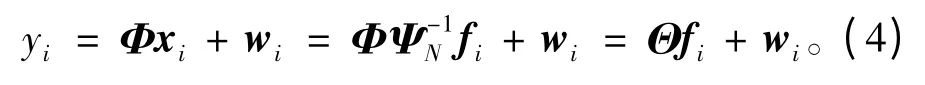
其中:Φ为AIC的采样矩阵;Θ为压缩感知矩阵;wi为观测噪声，wi～N(0，β-1)。对宽带信号的采样、重构和检测过程如图2所示。其中，λ为检测门限;分别表示子信道p被PU占用和未被占用。

图2 压缩频谱感知框架Fig.2 The structure of compressed spectrum sensing

各SU分别利用AIC对接收信号{xi进行压缩采样，融合中心(fusion center，简称FC)同步接收各SU的观测向量{，并由观测向量{yi重构出信号频谱。根据重构的信号频谱［p］，计算第i个SU重构的信号频谱在子信道p的能量统计Ti，p=‖fi［p］，然后各子信道进行能量检测，即Ti，p与检测门限比较来判断该信道是否被占用。

由于L个SU具有相同的观测矩阵Φ，则其压缩采样过程的MMV形式为:

其中:Y=［y1，y2，…，yL］为观测矩阵;X=［x1，x2，…，xL］为L个SU接收的宽带信号集合;F=［f1，f2，…，fL］为宽带信号的频谱集合。符合DCS的第二联合稀疏模型(JSM-2)，则的非零元素位置相同，且非零元素只集中在极少的子信道，即F具有块稀疏性。如图3所示，第p(p=1，2，…，P)个子信道的信号频谱集合为F［p］∈RS×L。

图3 信号频谱的块稀疏结构Fig.3 Block sparse structure of signal spectrum

各子信道信号频谱集合组合形式为:

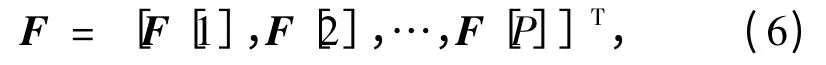
其中，F［p］=［F(p-1)S+1，F(p-1)S+2，…，FpS］T。相应地，压缩感知矩阵Θ的子矩阵组合的形式为:

其中;Θ［p］=［θ(p-1)S+1，θ(p-1)S+2，…，θpS］T;θn为矩阵Θ的第n列。因此，从观测矩阵Y重构出F，MBSBL是求解式(5)的一种有效方法。

2 MBSBL-FMLM算法

2.1 MBSBL框架

在MBSBL框架下，Fp的矩阵变量高斯分布式为:

其向量表达式为:

其中，γp为块Fp稀疏性的非负参数。当γp=0时，对应的块Fp为0。γpIS·L=IL⊗γpIS。为了快速实现算法，忽略块内联系和用户间的联系，F的先验概率分布式为:

其中，

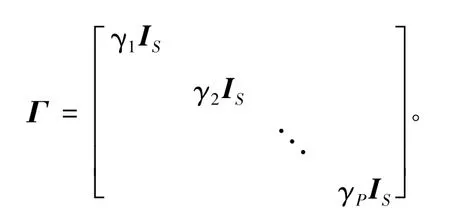
观测矩阵Y的后验概率分布式为:

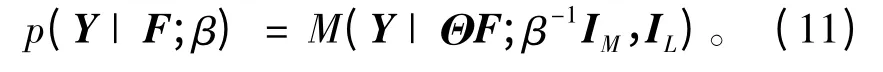
根据式(10)、(11)可知，F的后验概率分布服从:

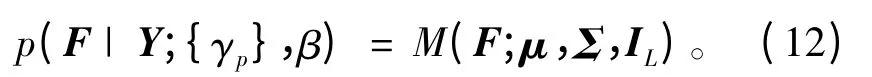
其中，

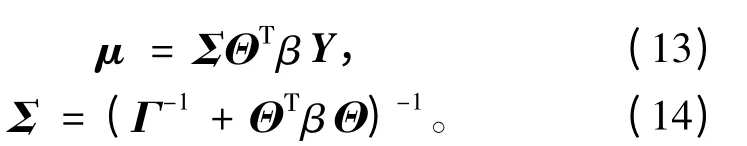
利用代价函数L({γp，β)，根据第二类最大似然估计法则估计参数{γp，β:

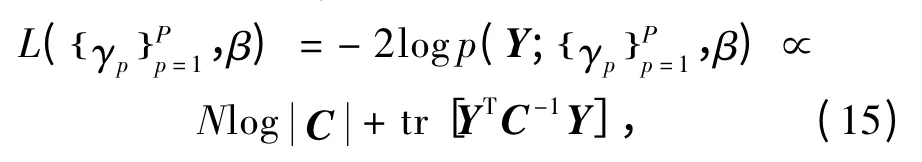
其中，

2.2 FMLM方法

利用FMLM方法优化L({γp，β)，式(16)可表示为:

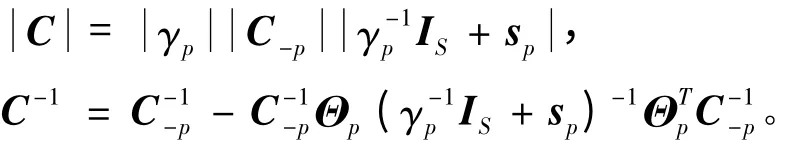
式(15)可表示为:

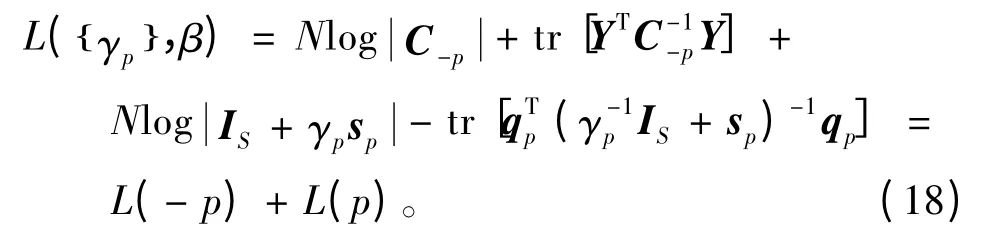
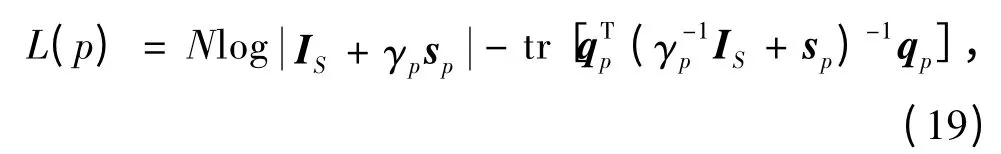
通过优化L(p)更新γp，

3 基于MBSBL-FMLM的宽带协作频谱感知算法流程

输入:Y、Θ、η;初始化:β-1=0.01‖Y，sp。宽带协作频谱感知算法步骤为:

2)计算ΔL(p)=L()-L(γp);

5)判断是否满足代价函数最大变化小于门限η，若满足条件，执行步骤6)，否则进入下一循环l=l+1;

6)满足终止条件，输出μ。

每次迭代过程中，仅更新使式(18)下降至最深的块信号，然后重新计算参数，其步骤类似于文献［12］的边缘似然函数最大化方法。该算法的终止条件为代价函数最大变化值小于门限η。

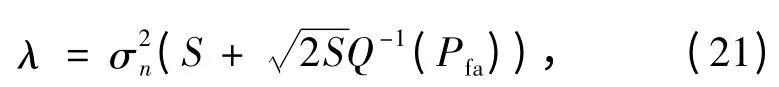
定义检测概率Pd为多用户多信道检测概率的平均值，

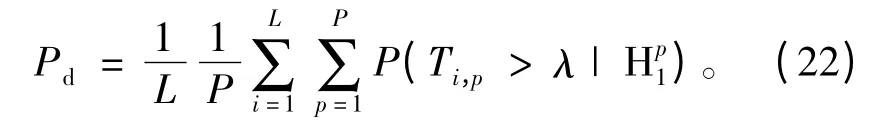
4 数值分析

利用归一化均方误差(normalized mean squared error，简称NMSE、检测时耗及检测概率(Pd)三个指标来分析MBSBLFMLM算法的频谱检测性能，并与SOMP算法进行比较。假设宽带信道长度为128 MHz，将其划分为16个互不重叠的子信道，信号长度N=512，每个子信道的信号长度为32。PU随机占用5个子信道，该宽带信道为AWGN信道，且信噪比RSN=10 dB，Φ为高斯随机矩阵。经过反复实验，MBSBL-FMLM算法的收敛门限设定为η=10-4，SOMP算法的误差门限设定为ε=10-2，每个仿真实验独立运行200次。

图4为在不同压缩比条件下MBSBL-FMLM算法和SOMP算法的NMSE比较。MBSBL-FMLM算法和SOMP算法的NMSE随压缩比的增加而降低，在相同的压缩比下，MBSBL-FMLM算法的NMSE远低于SOMP算法，即使在压缩比为0.25时，MBSBL-FMLM算法的NMSE都小于0.5。这是由于MBSBL-FMLM算法利用信号的块结构，并采用稀疏贝叶斯学习方法对信号进行重构，获得了更好的重构质量。

图4不同压缩比下NMSE的比较Fig.4 The comparison of NMSE in different compressed ratios

图5为在不同压缩比条件下MBSBL-FMLM算法和SOMP算法的平均感知时耗比较。从图5可看出，在相同的压缩比下，MBSBL-FMLM算法的平均感知时耗远低于SOMP算法，SOMP算法的平均感知时耗随压缩比增加而增加，而MBSBL-FMLM算法的平均感知时耗随压缩比的增加几乎不变。随着压缩比从0.25增加到0.5，SOMP算法的感知时耗从1 s增加到3.5 s，但MBSBL-FMLM算法的感知时耗几乎保持不变，且低于0.5 s。这是由于随着压缩比的增加，MBSBL-FMLM算法的迭代次数几乎不变，且远低于SOMP算法的迭代次数。

图5不同压缩比下平均感知时耗的比较Fig.5 The comparison of average sensing time in different compressed ratios

图6为在给定允许最大虚警概率Pfa=0.05，参与协作的SU数量L=2的情况下，不同压缩比条件下MBSBL-FMLM算法和SOMP算法的Pd比较。从图6可看出，MBSBL-FMLM算法和SOMP算法的Pd随压缩比增加而提高。在压缩比为0.3时，MBSBLFMLM算法的Pd达到100%，压缩比为0.375时，SOMP算法的Pd才接近100%。因此，要达到相同的Pd，MBSBL-FMLM算法所需的采样点数要低于SOMP算法。

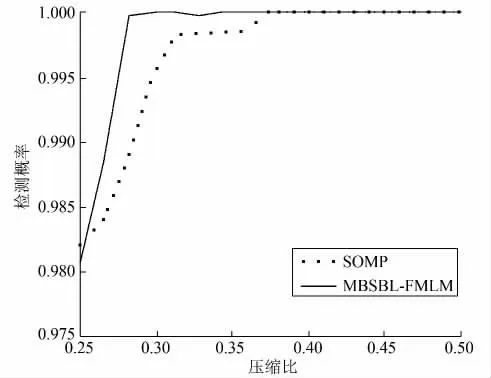
图6不同压缩比下检测概率的比较Fig.6 The comparison of detection probability in different compressed ratios

图7为参与协作的SU数量分别为L=1，3，5条件下的MBSBL-FMLM算法Pd的比较。从图7可看出，随着用户数的增加Pd大幅提升。当L=3，压缩比为0.25时，Pd达到0.99以上;L=5时，压缩比为0.25时，Pd达到0.97以上;压缩比为0.26时，Pd接近100%;而L=1，在压缩比为0.36时，Pd才接近100%。因此，基于DCS的多用户协作感知可解决单点检测存在的问题，同时降低各SU的采样压力。

图7 感知用户数不同情况下的检测概率比较Fig.7 The comparison of detection probability in different numbers of secondary users

5 结束语

为提高宽带压缩频谱感知算法的准确性和实时性，建立基于DCS的块稀疏信号协作频谱感知系统模型，提出了基于MBSBL-FMLM的宽带协作频谱感知算法，该算法考虑了信号的块稀疏结构，可获得很好的重构质量。另外，该算法忽略了块内联系和用户间的联系，通过FMLM方法估计参数，可实现信号的快速重构。数值分析表明，MBSBL-FMLM算法的检测概率、归一化均方误差和检测时耗均优于SOMP算法，且多用户协作频谱感知可缓解次用户的采样压力，同时提高检测性能。

［1］Tian Z，Tafesse Y，Sadler B M.Cyclic feature detection with sub-Nyquist sampling for wideband spectrum sensing［J］.IEEE Journal of Selected Topics in Signal Processing，2012，6(1):58-69.

［2］Mistry S，Sharma V.New algorithms for wideband spectrum sensing via compressive sensing［C］//IEEE International Conference on Communications，2013:2595-2600.

［3］Ariananda D D，Leus G.Compressive wideband power spectrum estimation［J］.IEEE Transactions on Signal Processing，2012，60(9):4775-4789.

［4］Wang Y，Pandharipande A，Polo Y L，et al.Distributed compressive wide-band spectrum sensing［C］//Information Theory and Applications Workshop，2009:178-183.

［5］Eldar Y C，Mishali M.Robust recovery of signals from a structured union of subces［J］.IEEE Transactions on Information Theory，2009，55(11):5302-5316.

［6］Duarte M F，Sarvotham S，Baron D，et al.Distributed compressed sensing of jointly sparse signals［C］//Thirty-Ninth Asilomar Conference on Signals，Systems and Computers，2005:1537-1541.

［7］Wei W，Min J，Qing G.A compressive sensing recovery algorithm based on sparse Bayesian learning for block sparse signal［C］//International Symposium on Wireless Personal Multimedia Communications，2014:547-551.

［8］Liu B，Zhang Z，Xu G，et al.Energy efficient telemonitoring of physiological signals via compressed sensing:a fast algorithm and power consumption evaluation［J］.Biomedical Signal Processing and Control，2014，11:80-88.

［9］张正浩，裴昌幸，陈南，等.宽带认知无线电网络分布式协作压缩频谱感知算法［J］.西安交通大学学报:自然科学版，2011，45(4):67-71.

［10］Patil K，Prasad R，Skouby K.A survey of worldwide spectrum occupancy measurement campaigns for cognitive radio［C］//International Conference on Devices and Communications，2011:1-5.

［11］Ji S，Xue Y，Carin L.Bayesian compressive sensing［J］.IEEE Transactions on Signal Processing，2008，56(6):2346-2356.

［12］Tipping M E，Faul A C.Fast marginal likelihood maximisation for sparse Bayesian models［C］//Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics，2003:2595-2602.

［13］王璐瑜，朱琦.基于DSCS的宽带频谱感知新算法［J］.信号处理，2011，27(6):813-819.