直线电机速度和加速度的复合前馈控制

李万周，侯伯杰，高建设，王帅

(郑州大学机械工程学院，河南郑州450001)

0 前言

直线电机是一种将电能直接转化为直线运动机械能，而不需要任何中间转换机构的传动装置，它可以看作是将传统旋转电机沿径向剖开，然后将电机的圆周展开成直线形成的，如图1所示。

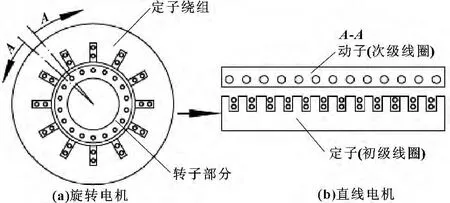
图1 旋转电机到直线电机的演变

与传统旋转电机相比，直线电机由于具有传动直接、体积小，结构简单、低磨损、精度高、速度不受限制等优点，已经被广泛地应用于生产制造和日常生活等多领域，尤其适用于如芯片制造、集成电路、高速高精加工、物料运输、精密仪器等方面。直线电机伺服系统通常采用PID位置跟踪反馈控制的方式，但是随着对控制精度的要求不断地提高，一般的PID控制由于控制精度的限制、负载扰动等因素的影响，控制效果往往不能达到预期效果。本文作者针对这种情况提出了自适应速度+加速度前馈补偿的复合前馈+ PID控制的策略，保留了原有PID控制的特性又能充分利用速度前馈和加速度前馈控制的优点，使直线电机能够更好地应用于高速、高精的运动控制中。

1 复合控制

反馈控制是根据系统的输入和输出之间的偏差来进行误差补偿的控制。由于反馈控制总是将系统的输出反馈和输入作比较后进行控制，其控制存在一定的滞后，这种滞后虽能满足对速度、控制精度要求不高的一般系统，但是对于速度和精度要求严格的系统，即使微小的滞后也能引起很大的偏差，结果导致控制的效果差强人意。

与反馈控制不同，前馈控制是基于扰动信号的控制，在扰动还未影响输出之前改变操作量，使系统对误差具有一定的预见性。复合控制是将反馈控制和前馈控制结合起来的控制方式，它能够综合两种控制方式的优点，使得随动系统的跟踪精度大为提高。复合控制的前馈方式一般包括扰动补偿、输入补偿，在高精度的控制系统中，跟踪误差主要是输入信号造成的，并且系统的扰动信号是很难测量的，若对扰动信号补偿可能得不偿失，因此一般选择对输入信号进行输入补偿的复合控制方式，其控制原理框图如图2。

图2 复合控制系原理框图

其中:G(s)为被控对象的传递函数，GC(s)为控制器的传递函数，GF(s)为输入补偿传递函数，H(s)反馈通道传递函数。被控信号输出y(t)的拉氏变换为:

由上式求出复合控制系统的传递函数Φ(s)为:

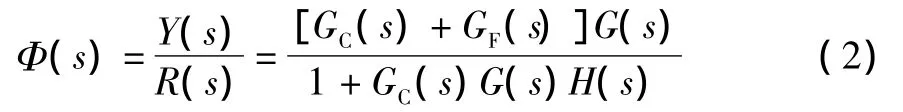
取H(s)=1，上式可简化为:

由式(3)可看出:输入补偿并的引入并不会影响系统的特征方程，因此前馈补偿并不会影响系统的稳定性，与此同时还可以显著提高系统的控制精度。从这点也可以看出引入前馈补偿后的复合控制比单纯的反馈控制的优越之处。

2 PID控制原理

在模拟的控制系统之中，最常见也最成熟的控制模型是PID控制模型，其控制系统的原理框图如下图3。

图3 PID控制系统的原理框图

PID控制器是一种线性控制器，它根据给定值r(t)和实际输出值y(t)组成控制偏差:

连续性PID的控制规律为:

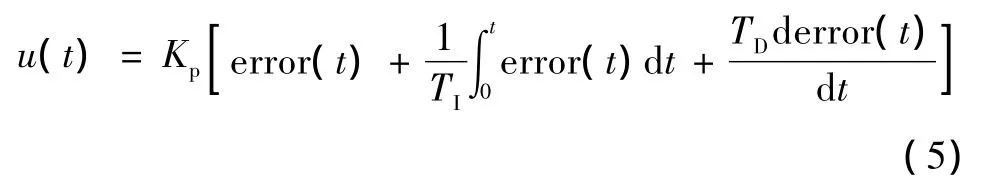
写成传递函数的形式:

式中:Kp为比例系数;TI为积分时间常数;TD为微分时间常数。

简单说来，PID控制器的控制主要包括:比例环节、积分环节及微分环节，通过对这的3个环节控制参数Kp、TI、TD的整定和优化，一般就能够使得控制系统的性能达到要求，对这3个参数的整定在文中不再赘述。

3 直线电机的数学模型

直线电机工作时候产生的推力原理和旋转电机类似，由上文可知，直线电机可以看成将一台旋转电机沿径向剖开后沿着圆周展开成直线而形成特殊的旋转电机，电流通过初级和次级线圈的电流作用产生电磁推力的作用。其初级线圈、次级线圈、动子、定子、光栅尺的结构和动子受力如图4所示。

图4 直线电机结构和动子受力分析

直线电机在工作的时候，动子主要受到电机驱动力Fe、导轨的摩擦力和阻尼力f等作用，动子运动系统运动学方程为:

综上，可以得出直线电机系统运动的控制过程中直线电机的机械传递函数为:

文中所用直线电机的主要参数见表1。

表1 直线电机主要性能参数

4 自适应速度+加速度复合前馈控制和MATLAB仿真

4.1 加速度+速度复合前馈控制

根据复合前馈的原理和PID控制的原理，文中建立自适应速度+加速度前馈补偿的复合控制+PID控制系统，其原理方框图如图5所示，其中vel、acc和pos分别表示系统预设直线电机运动的速度前馈补偿、加速度前馈补偿和位置信号，这3个信号通过调用MATLAB工作空间设定的值进行仿真。

图5 加速度和速度复合前馈+PID控制系统原理框图

常用加速度或速度前馈系数的标准计算方法一般基于精确模型，但由于建模误差，电机推力常数、摩擦因数等存在计算误差，因此无法得到准确的前馈系数，为此本文采用自适应的调节方式。

4.2 自适应前馈系数求解

在式 (10)给出了一种基于PID控制模型的前馈系数求解方法［6］，该方法中前馈系数β不是固定不变的，第k个伺服周期中的前馈系数利用前k个伺服周期中的PID控制器输出进行在线修正，即:

Δβ(k)为第k个伺服周期中前馈系数的补偿项。

其中:

PIDout(k)为PID控制器的输出，ρ为遗忘因子，取ρ=0.9［6］，qd(k)是第k个伺服周期的加速度或者速度设定值，若用分别为被控对象的速度和加速度，便能得到加速度和速度前馈系数自适应求解方法。

系统模型PID控制各个环节的参数分别为:kp= 873 000;ki=757 000;kd=64 500。

为说明引入前馈补偿之后的系统的控制性能的优越性，首先看一下系统模型在单纯反馈控制和引入前馈后复合控制的阶跃响应，如图6所示，其中实线为复合控制的响应曲线，虚线为单纯反馈控制响应曲线。可以看出，引入前馈的复合控制较单纯反馈控制的调整时间明显缩短，超调量也有大幅度降低。

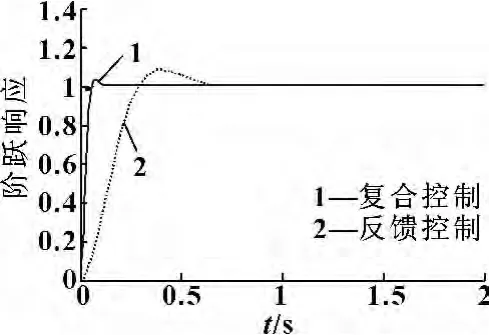
图6 反馈控制和复合控制阶跃响应

文中采用升降速的曲线进行MATLAB仿真，直线电机运动的加速度 (acc)、速度 (vel)以及位置(pos)设定值分别为图7所示。

图7 升降速曲线仿真的速度、加速度、位置信号设定值

MATLAB仿真结果的误差曲线如图8。

图8 升降速曲线的不同控制方式MATLAB仿真误差

图中曲线4为单纯PID反馈控制的误差曲线，曲线3为仅引入速度前馈补偿的误差曲线，曲线2为仅引入加速度前馈补偿后的误差曲线，曲线1为引入自适应速度+加速度前馈补偿后的复合控制误差曲线。

加速度和速度前馈系数自适应变化过程如图9所示。

图9 加速度和速度前馈系数自适应变化过程

由图9可见，引入速度+加速度前馈的复合控制在升降速曲线的升速和降速阶段的误差均小于仅引入加速度或速度前馈补偿以及单纯反馈控制情况下的误差，当有较大的加速度时其调整时间明显短于其他控制，可以很快控制误差减小到微米级以下，并且动态和静态的稳定性也优于其他控制方式。

5 实验及结论

实验在某微纳公司二维直线电机实验平台进行，位置检测采用光栅尺，分辨率为1 μm，实验用到的电机为X轴电机动子型号为WMM-06030S，使用的控制驱动器为Elmo HAR-5/60，控制系统结构如图10所示。

图10 直线电机实验系统复合控制结构图

直线电机实验系统装置组成如图11所示。

图11 直线电机实验系统装置和PID参数值设定界面

图12中位置误差的纵向为光栅检测的直线电机位置跟踪的误差，其中光栅检测的精度为1 μm，即电机的位置跟踪误差峰值控制在3 μm以内。由此，自适应速度+加速度复合PID前馈的控制方式能使直线电机的位置控制精度达到很大的提高，而且还具有良好的响应速度，能够满足对精度和速度要求更高的直线电机运动控制中。

图12 直线电机复合控制的升降速实验动子位置误差

［1］叶云岳，直线电机原理及应用［M］.北京:机械工业出版社，2000:142-150.

［2］李友善，自动控制原理［M］.2版(上册).北京:国防工业出版社，2003:107-111.

［3］刘金琨，先进PID控制及其MATLAB仿真［M］.3版.北京:电子工业出版社，2011:81-84.

［4］侯伯杰，直线电机伺服系统的复合前馈PID控制［J］.机床与液压，2009，37(2):56-58.

［5］赖国庭，吴玉厚，富大伟.基于PMAC的直线电机速度/加速度前馈控制［J］.控制工程，2003，10(6):556-557.

［6］李鑫，杨开明，朱煜，等.平面电机自适应加速度前馈运动控制［J］.电机与控制学报，2012:95-100.

［7］韩金恒，潘松峰，高菲，等.基于PMAC伺服系统的PID -前馈算法及其参数调节［J］.信息技术与信息化，2008(5):556-557.

［8］KIMA Moojong，KIMB Jinyoung，LEEA Moon G.Design of Feedforward Controller to Reduce Force Ripple for Linear Motor using Halbach Magnet Array with T Shape Magnet.Physics Procedia，2011(19):352-356.

［9］SEIDLER R D，NOLL D C，THIERSA G.Feedforward and Feedback Processes in Motor Control［J］.NeuroImage，2004(22):1775-1783.