三自由度并联机构性能分析与优化

张晓菊，张春友，吴晓强，于立波

(1.河套学院机电工程系，内蒙古巴彦淖尔015000; 2.内蒙古民族大学机械工程学院，内蒙古通辽028000; 3.郑州宇通客车股份有限公司，河南郑州450000)

0 前言

空间三自由度并联机构具有结构简单，经济成本低，运动精度高等优点。目前，并联机构的优化设计主要集中在工作空间、灵巧性、可操作度、各向同性、刚度等方面。近年来国内外许多学者对性能指标的研究越来越多，KUCUK等［1］采用遗传算法对三自由度并联机构灵巧性和可操作度进行了可行性设计研究;ZENG等［2］对三自由度并联机构3-PRUR进行了各向同性、速度性能、承载能力等进行了优化分析; JOSHI等［3］对三自由度3UPU和3UPS-UP并联机构的工作空间和全域条件数进行了优化比较分析;SICILIANO［4］基于可操作度对3-UPS-UP并联机构进行了尺度综合研究。

本文作者对三自由度 (两转一移)并联机构3-UPS-PU、4-UPS-PU的全域灵巧指标和全域刚度进行了优化设计与分析，利用粒子群优化算法对结构参数进行优化分析，最终得到性能指标在整个工作空间的最优Pareto解。结果表明，4UPS-PU冗余并联机构比3UPS-PU具有较好的灵巧指标和刚度指标。

1 机构模型的建立

1.1 3UPS-PU机构模型的描述

并联机构3UPS-PU由动平台、静平台及3条驱动分支和中间一条约束分支组成，如图1所示。动平台球铰铰点a1、a2、a3，a1a2a3为等边三角形，静平台胡克铰铰点A1、A2、A3，A1A2A3也为等边三角形，动静平台的外接圆半径分别为r、R。由于中间支链的约束，对动平台有3个运动约束;于是动平台有3个自由度，即绕X轴和Y轴转动和沿Z轴的移动。

图13 -UPS-PU并联机构结构简图

参考坐标系OXYZ固定于静平台，原点O位于等边三角形的几何中心，X指向A1，Y轴平行于A2A3，Z轴垂直向上;动坐标系oxyz固接于动平台，原点o位于a1a2a3构成的等边三角形的中心，x轴沿oa1方向，y轴平行于a2a3，z轴垂直于动平台向上。初始位姿时，两坐标系轴线平行，动静平台之间的距离为d。

1.2 4UPS-PU机构模型的描述

4UPS-PU空间3自由度并联机构由动静平台和连接动静平台的5个分支组成。静平台通过4个结构完全相同的驱动支链UPS(虎克铰-移动副-球副)以及1个中间含恰约束支链PU(移动副-虎克铰)与动平台连接。通过改变4个驱动杆的长度，机构可以在一定的工作空间范围内实现二维转动和一维移动。动平台球铰铰点b1、b2、b3、b4，静平台虎克铰铰点B1、B2、B3、B4，动静平台的半径分别为r、R。结构简图如图2所示。

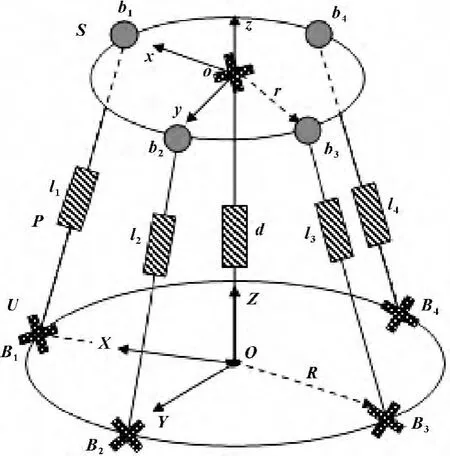
图2 4UPS-PU并联机构结构简图

在并联机构的动静平台上分别建立坐标系，参考坐标系OXYZ固定于静平台，坐标系的中心为4个均匀分布的胡克铰所在外接圆的圆心，其中，X轴指向B1，Z轴垂直向上，Y轴方向按右手定则给定。动坐标系oxyz建立在动平台，初始位置x轴与X轴方向相同，y轴与Y轴方向相同，z轴与Z轴方向相同，动静平台之间的距离为d。

2 机构的运动学求解

2.1 3UPS-PU位置逆解和雅可比求解

如图1所示，动平台铰点ai在动坐标系下的位置矢量为

静平台球铰铰点Ai在参考坐标系下的位置矢量为

动坐标系原点o在参考坐标系中的位置矢量为

动平台铰点ai相对于动坐标系下的位置矢量在参考坐标系下可以表示为

其中，利用组合变换RPY可得旋转矩阵Q为

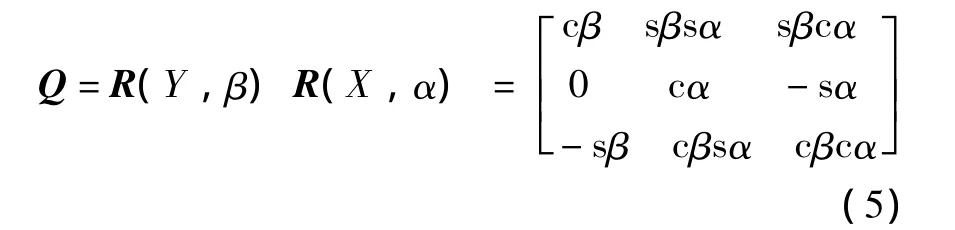
式中:sα=sinα，cα=cosα，其余类似。

并联机构的驱动杆长矢量为

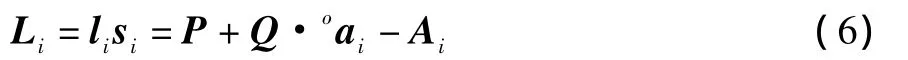
其中:li为驱动杆的长度;si为杆的单位向量。

对等式(6)求导，可得

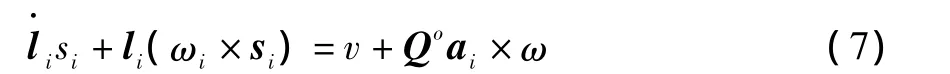
其中:v为动平台的速度;ω为动平台的角速度。

等式(7)两边点乘si，可得

写成矩阵的形式

则并联部分的雅可比矩阵为

2.2 4UPS-PU位置逆解和雅可比求解

针对4UPS-PU并联机构，根据坐标变换理论，有

其中:旋转矩阵Q和动平台参考点o的坐标值同3UPS-PU机构。

由几何关系，可知杆长的矢量为

杆长的平方为

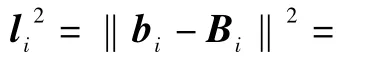
对等式 (14)两边求导数，整理可得

则并联部分的雅可比矩阵为

2.3 串联PU支链的雅可比矩阵求解

考虑中间被动约束支链，可以看成串联机构，等效成P-R-R，运动结构如图3所示。

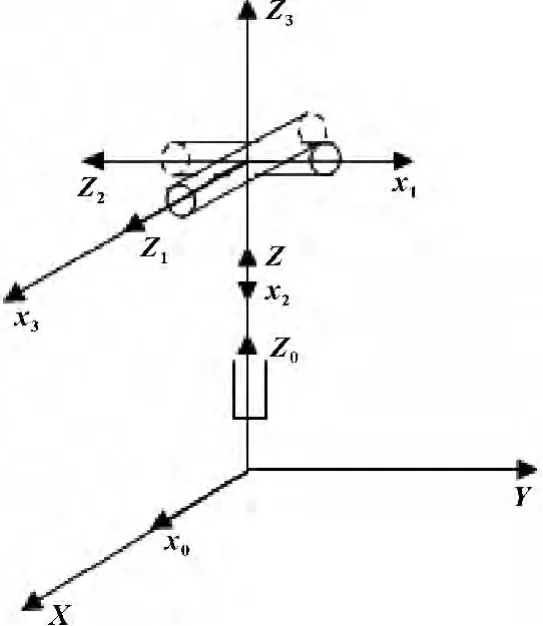
图3 中间PU支链运动简图

采用D-H法可得到从固定坐标系到运动坐标系的齐次变换矩阵T，

中间被动PU约束支链的D-H参数见表1。

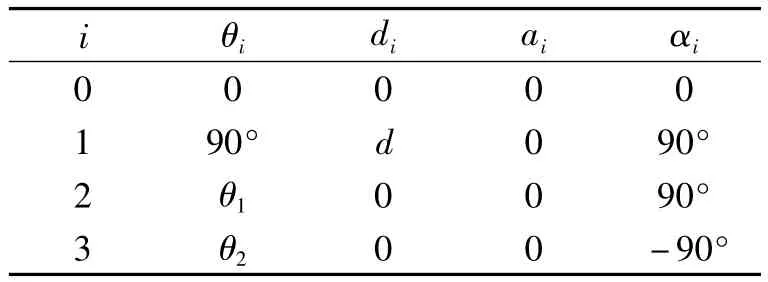
表1 中间被动约束支链的D-H参数表

雅可比矩阵可以分解为

其中:Jli为线速度雅可比;Jai为角速度雅可比。若i为移动关节时，若为转动关节时，

其中，bi=Q0…Qi-1b，［ri1］T=［x y z 1］T-T0…Ti-1r，b=［0 0 1］T，r=［0 0 0 1］T

则串联部分的雅可比矩阵为

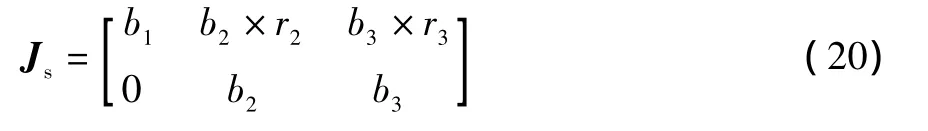
则并联机构总的雅可比矩阵为

3 性能指标的建立

3.1 全域灵巧指标

雅可比矩阵的条件数可以定义为

式中:J为雅可比矩阵;‖·‖为矩阵的谱范数。

条件数是不同位姿下性能指标的局部反映，无法衡量机构控制精度的好坏。GOSSELIN等［5］提出全域条件指标，总体评价机构在空间内的整体性能，定义为雅可比矩阵条件数倒数的积分与工作空间体积的比值，即

其中:W为工作空间。

GPI∈(0，1］，GPI越大，说明机构在整个工作空间内的灵巧性和控制精度越高，机构性能越佳。

3.2 全域刚度指标

并联机构的静刚度是指动平台处的输出刚度，刚度的驱动映射方程可以表示为

其中:τ为驱动副处的驱动力旋量;Δq为相应关节的变形;k为刚度系数，设为常数，k=1 000。

则刚度矩阵可以表示为K

则机构的局部刚度为

则全域刚度指标［6］可以定义为

4 优化建模

4.1 优化算法

粒子群优化 (Particle Swarm Optimization，PSO)又称微粒群算法［7］，采用粒子群在确定空间中追随最优粒子进行搜索，寻找个体极值pbest和全局极值gbest，最终达到目标函数决定的适应值的过程，参数配置见表2。

表2 粒子群优化算法配置表

4.2 优化模型的建立

3UPS-PU、4UPS-PU两种并联机构的尺寸变量为动平台半径为r，静平台半径为R，动静平台高度z，以及驱动支链lmax。由于lmax与性能指标的计算无关，只是在确定工作空间范围内使用，lmax越大，工作空间必然越大，因此，lmax无须作为优化尺寸参数，在机构工作条件满足的情况下尽可能增大时lmax来增大工作空间［8］。所以机构优化参数X=［r，R，z］

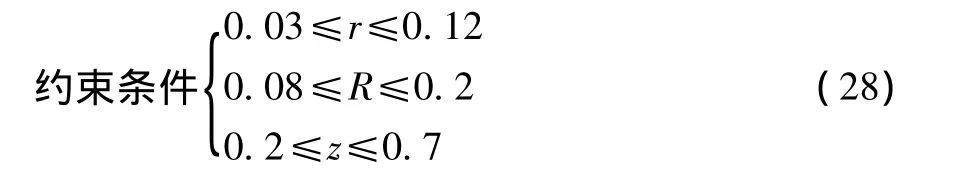
目标函数F=［GPImax，GSImax］

4.3 优化结果分析

在目标函数的寻优过程中可以得到设计变量的变化曲线和性能指标的变化曲线，如图4、5、6所示。

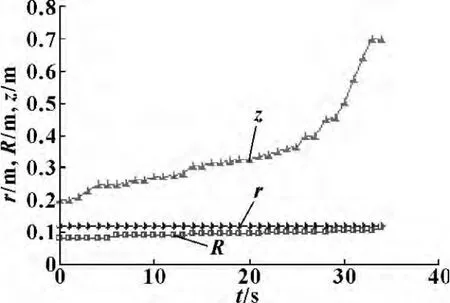
图4 Pareto解与设计变量的变化曲线

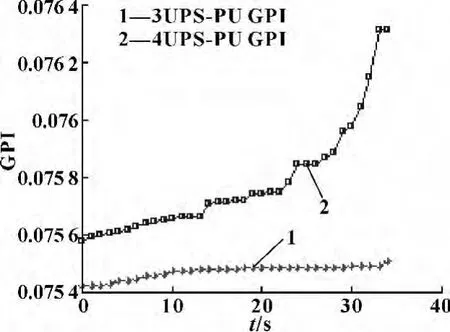
图5 Pareto解与全域灵巧指标的变化曲线

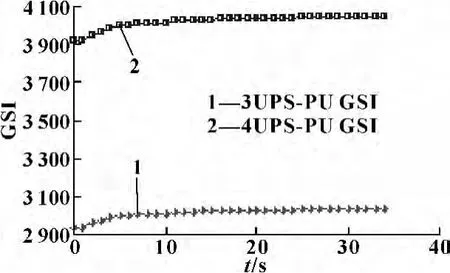
图6 Pareto解与全域刚度指数的变化曲线

从图4可以看出，在进行粒子群优化求解过程中，设计变量最终达到平衡，取得最优Pareto解。图5和6可以看出4UPS-PU冗余驱动并联机构比3UPSPU并联机构具有较好的全域灵巧指标和全域刚度指标。

设计变量r、R对全域灵巧指标和全域刚度指标的影响图谱［9-10］，如图7所示。

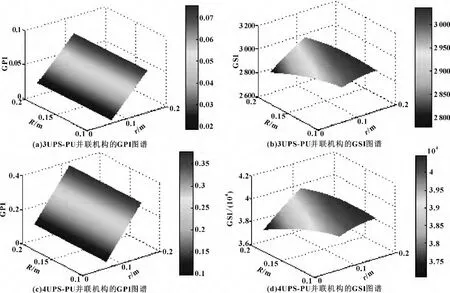
图7 设计变量r、R与性能指标GPI、GSI的影响图谱

基于粒子群优化算法，分别搜索两种并联机构的 最优结构参数和最优目标函数的Pareto解，见表3。

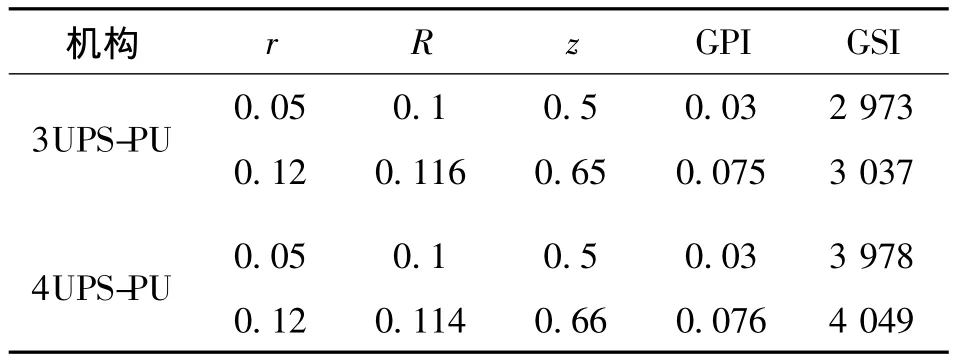
表3 两种并联机构优化结果比较

结合图7和表3中可以看出，3UPS-PU并联机构和4UPS-PU冗余并联机构的全域灵巧指标优化后明显提高，增大了约1.5倍，但全域刚度指标增加甚少;4UPS-PU冗余并联机构的全域刚度比3UPS-PU并联机构明显增强，说明冗余驱动可以提高机构的刚度。

5 结论

(1)对两种并联机构3UPS-PU、4UPS-PU进行了运动学分析，建立运动学模型和数学模型，考虑中间约束支链的影响，建立完整的雅可比矩阵;

(2)建立全域灵巧指标、全域刚度指标，采用粒子群优化算法对两种并联机构进行优化比较，得到Pareto解与设计变量和目标函数的变化曲线;

(3)4UPS-PU冗余并联机构相比3UPS-PU并联机构，具有较好的全域灵巧性能和全域刚度性能。

［1］KUCUK Serdar.A Dexterity Comparison for 3-DOF Planar Parallel Manipulators with Two Kinematic Chains Using Genetic Algorithms［J］.Mechatronics，2009，19(6):868-877.

［2］ZENG Daxing，HUANG Zhen，LU Wenjuan.Performance A-nalysis and Optimal Design of a 3-DOF 3-PRUR Parallel Mechanism［J］.Journal of Mechanism Design，April，2008，130(4):042307.

［3］JOSHI Sammer，Lung-TASI Wen.A Comparison Study of Two 3-DOF Parallel Manipulators:One With Three and the Other With Four Supporting Legs［J］.IEEE Transactions on Robotic and Automation，2003，19(2):200-209.

［4］SICIANO Bruno.The Tricept robot:Inverse Kinematics，Manipulability Analysis and Closed-loop Direct Kinematics Algorithm［J］.Robotica，1999，17(4):437-445.

［5］ANGLES J，GOSSELIN C.A Global Performance Index for the Kinematic Optimization of Robotic Manipulators［J］.Journal of Mechanical Design，1991，113(3):220-226.

［6］LIU X J，JIN Z L，GAO F.Optimum Design of 3-DOF Spherical Parallel Manipulators with Respect to the Conditioning and Stiffness Indices.Mechanism and Machine Theory，2000，35(9):1257-1267.

［7］赖宇阳.Isight参数优化理论与实例详解［M］.北京:北京航空航天大学出版社，2012.

［8］付萌.少自由度并联机构尺度参数的多目标优化研究［D］.成都:电子科技大学，2013.

［9］李艳，王勇.基于影响系数法的冗余驱动并联机器人速度分析［J］.组合机床与自动化加工技术，2009(8): 15-18.

［10］LIU Xinjun，WANG Jinsong，PRITSCHOW G.Performance Atlases and Optimum Design of Planar 5R Symmetrical Parallel Mechanisms［J］.Mechanism and Machine Theory，2006，41(2):119-144.