角钢码垛机械手机构分析与优化

王龙宇，李占贤，何凯杰

(河北联合大学机械工程学院，河北唐山063009)

0 前言

随着钢铁工业连续化和大型化的不断发展，为提高作业率，减少故障率，节能降耗，改善产品质量，生产国民经济发展急需的新品种，许多环节都已非人力所能及，自动化装备已经成为钢铁工业不可或缺的关键设备，成为提高生产力的重要要素之一。

角钢是一种常见的建筑结构和工程结构材料，主要用于金属构件及厂房的框架，广泛应用于各种房梁、桥梁、输电塔、起重运输机械、船舶以及仓库货架等场合。角钢的轧制生产中，在矫直后打捆前的环节就是码垛，现在很多钢铁企业中，有的还在采用原始的人工码垛，工人劳动强度大、码垛效率低下，而且码垛效果不好、参差不齐，影响产品的外观质量，不便于后续运输，而且很容易使产品变形。由于人力存在的缺陷，严重制约着码垛效率和码垛质量，而现有的角钢码垛机体积庞大，生产效率低下，容易出错，已经成为影响钢铁企业生产效率的关键因素。根据国内的现状，设计了一种角钢码垛机械手。该角钢码垛机械手占用体积小、快速准确，大大提高了码垛效率和码垛质量。

1 角钢码垛机械手的机械结构简介

角钢码垛机械手的机械结构如图1所示。

图1 角钢码垛机械手的机械结构简图

角钢码垛机械手由两个伺服电机通过丝杠控制末端手爪的运动。码垛机构的左边两个连杆等长，同时连杆与滑块连接点间距和与手爪连接点间距等长，因此，左边两个连杆、滑块、手爪构成了一个平行四边形。滑块保持水平在丝杠导轨上滑动，故手爪总能保持水平抓取。角钢生产线上，角钢一排排扣放向下水平传送到抓取位置，这就要求抓取装置必须总保持水平抓取［1］。该抓取装置符合角钢的生产工艺流程，同时也实现了角钢的顺利码垛。

2 角钢码垛机械手的运动学分析

机构的运动学是研究机构运动的几何关系，也是分析机构其他性能的基础。图1所示的角钢码垛机械手属于空间机器人，由于支链多，给运动学分析带来了困难。为此，依据几何投影学，将二自由度平移并联机器人等效成平面机构，可大大降低运动学分析的复杂性，如图2所示。

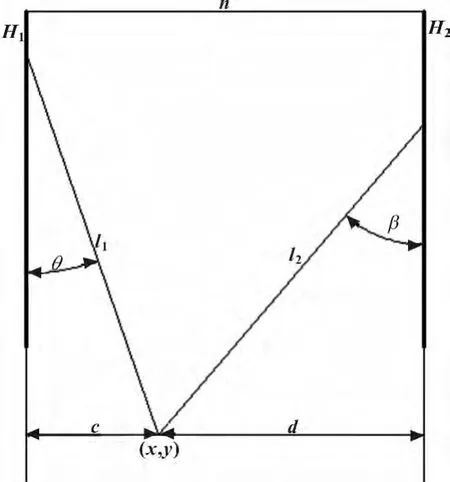
图2 角钢码垛机械手机构简图

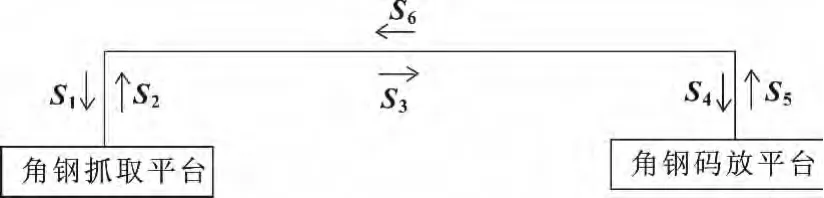
图3 末端执行器轨迹

根据角钢自动码垛机末端执行器的轨迹，将轨迹路线划分为六段。分别为S1=96 mm;S2=96 mm; S3=1 365 mm;S4=96 mm;S5=96 mm;S6=1 365 mm。同时对这六段的时间进行了规划。在码垛之前，需要等待时间 t0=1 s;S1段对应的运行时间为t01=0.5 s;S2段对应的运行时间为t12=0.5 s;S3段对应的运行时间为t23=2 s;因为S3段距离比较大，所以设计了匀速运行阶段。S3段匀加速运行时间为t231=0.25 s;S3段匀速运行时间为t232=1.5 s;S3段匀减速运行时间为t233=0.25 s;S4段对应的运行时间为t34=0.5 s;S5段对应的运行时间为t45=0.5 s; S6段对应的运行时间为t56=2 s;S6段匀加速运行时间为t561=0.25 s;S6段匀速运行时间为t562=1.5 s; S6段匀减速运行时间为t563=0.25 s。

根据速度和加速度公式，

可求得六段的位移、速度、加速度随时间的变化函数。

根据末端执行器的轨迹和位移随时间的变化，对H1和H2在丝杠上的位置变化进行分析和求解，如图2所示。

根据式(1)—(4)，可求得

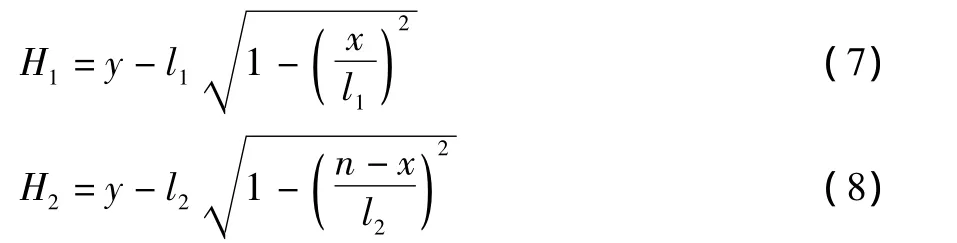
根据上面的计算和推导，用Matlab对其进行分析和求解，得到H1和H2随时间的变化如图4所示。

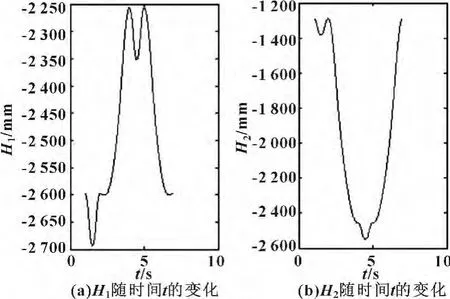
图4 H1和H2变化图

根据末端执行器的轨迹和位移随时间的变化，对H1和H2在丝杠上的速度变化进行分析和求解。

对H1进行速度雅可比求解，J1=jacobian(H1，［x，y］)，

对H2进行速度雅可比求解，J2=jacobian(H2，［x，y］)，

将H1和H2的速度雅可比进行合并，得

根据上述所求可得，v1=J1×v，v2=J2×v，用Matlab对其进行分析和求解，得到v1和v2随时间的变化图如图5所示。

图5 v1和v2变化图

根据末端执行器的轨迹和位移随时间的变化，对H1和H2在丝杠上的加速度变化进行分析和求解。

对H1进行海森矩阵求解，Ha1=jacobian(J1，［x，y］)，

对H2进行海森矩阵求解，Ha2=jacobian(J2，［x，y］)，

根据上述所求可得，a1=v'Ha1v+J1a;a2=v'Ha2v +J2a，用Matlab对其进行分析和求解，得到a1和a2随时间的变化图如图6所示。

图6 a1和a2变化图

根据图4—6的分析可知，H1、H2的位移、速度、加速度都偏大，与实际状况有一定差距。为了降低H1、H2的位移、速度、加速度，下面对机构的导轨进行倾斜设计与优化。

3 角钢码垛机械手导轨倾斜机构的设计

如图7所示为导轨倾斜机构简图。

图7 导轨倾斜机构简图

根据末端执行器的轨迹和位移随时间的变化，对H1和H2在丝杠上的位置变化进行分析和求解，如图7所示。

根据式 (13)—(17)和雅可比矩阵、海森矩阵，可求得 H1和 H2以及 v1、v2、a1、a2的表达式。

根据上面的计算和推导，用Matlab对其进行分析和求解，得到导轨倾斜角度γ和H1、H2、v1、v2、a1、a2的关系，如表1、2所示。

表1 γ和H1、H2的变化关系

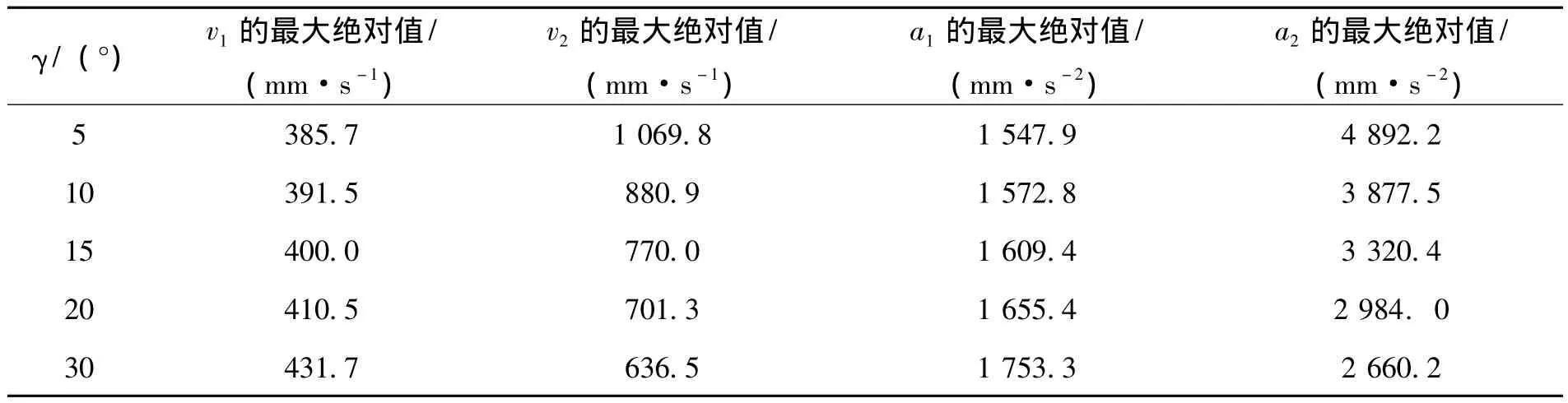
表2 γ和v1、v2、a1、a2的变化关系

根据图4—6以及表1、表2的分析可知，当倾斜角度越大，H1和H2的位移差值以及速度、加速度的最大绝对值越小，机构的稳定性越强。但根据实际情况，角钢码垛机 (图6)中的g=3 000 mm，f=500 mm。综合上述分析，当γ=15°时为最优倾斜角度，其位移、速度、加速度对比图如图8、9所示。

图8 H1的长度、速度、加速度对比图 (γ=15°)

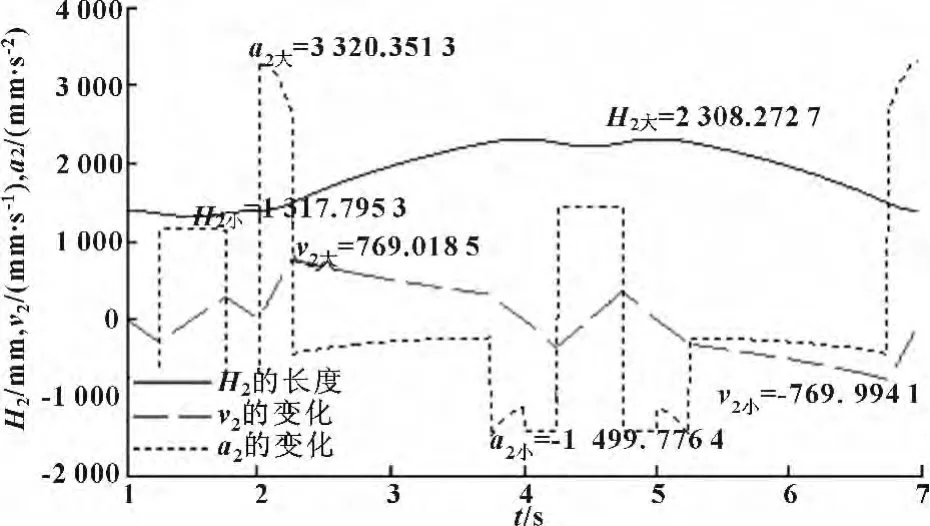
图9 H2的长度、速度、加速度对比图 (γ=15°)

4 结论

通过对角钢码垛机械手机构的优化，将码垛机械手导轨的倾斜角度γ由0°变为15°，码垛机械手H1和H2位移差值以及速度、加速度最大绝对值明显变小，减小了机械冲击和震动，提高了码垛机运行的平稳性，为角钢码垛机械手机构的优化提供了理论依据。

［1］李占贤，李晨辉，王志军，等.型钢自动码垛装置.中国专利:201310457782.7［P］.2013.

［2］李占贤.高速轻型并联机械手关键技术及样机建造［D］.天津:天津大学，2004.

［3］黄田，李占贤，李曚.仅含转动副的二自由度平动机器人机构.中国专利:00145160.2［P］.2001.

［4］黄真，赵永生，赵铁石.高等空间机构学［M］.北京:高等教育出版社，2006.

［5］高洪，赵韩.并联机器人机构学理论研究综述［J］.安徽工程科技学院学报，2006，21(1):73-79.