高层建筑幕墙安装机器人系统的运动学分析

岳建章，杨冬，王刚，樊旭，李铁军

(河北工业大学机械工程学院，天津300130)

0 前言

进入21世纪以来，我国城市化进程不断加快，越来越多的高层建筑拔地而起。建筑幕墙作为建筑物的主导性外围装饰品，越来越受到人们青睐，大量室外高空幕墙的安装工程为我国建筑装饰业带来新的发展契机。由于我国建筑业的整体机械化水平低，目前我国高空幕墙的安装大多依赖人工，不仅劳动强度大，而且危险性极高，极易出现高空坠落伤亡等各类安全事故［1-3］。针对上述问题，开展了高空幕墙安装的智能化施工装备的相关技术研究，旨在研发出适用于高层建筑幕墙安装的自动化施工设备。

本文作者简要介绍了该幕墙安装机器人的结构以及适应高空幕墙安装所采用的高空作业平台结构，重点进行了运动学分析，建立了运动学方程，求出了运动学正解和逆解，并进一步分析了机器人的工作空间，为幕墙安装机器人系统的控制提供了基础。

1 幕墙安装机器人系统简介

机器人系统是幕墙安装系统的重要组成部分，主要完成玻璃幕墙板材的抓取、搬运、位姿调整、以及安装等任务。由于工艺的需求，该机器人具有6个自由度，每个关节都由伺服电机加RV减速器驱动。

机器人的机械结构示意图如图1所示。

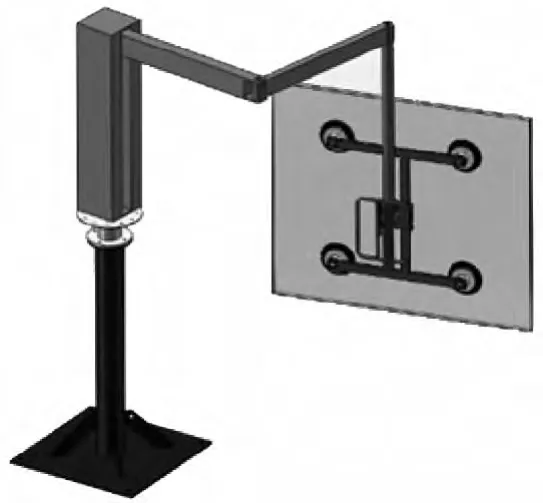
图1 幕墙安装机器人结构简图

机器人末端示意图如图2。

图2 机器人末端及传感器安装示意图

在幕墙安装机器人系统的基础上，为了适应高层建筑幕墙的安装需要，将幕墙安装机器人系统加入高空作业平台，平台的结构如图3所示。

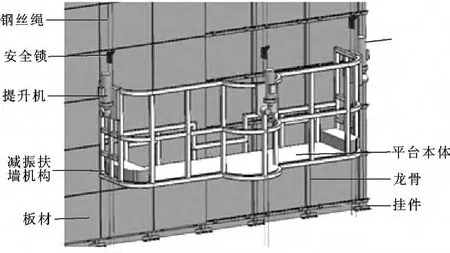
图3 吊篮式高空作业平台

2 幕墙安装机器人位姿矩阵的求解

根据D-H法则，给幕墙安装机器人建立必要的坐标系，如图4所示。

图4 关节坐标图

连杆参数及关节变量如表1所示。

表1 连杆参数及关节变量值

由D-H法则的理论知识，可以求出各个坐标系间的变换矩阵An:

将以上6个变换矩阵乘积得到幕墙安装机械手末端的位姿矩阵:

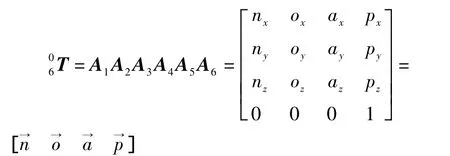
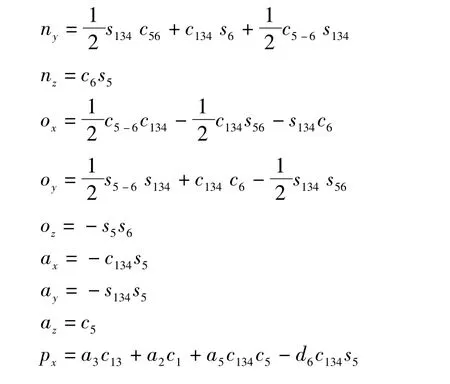
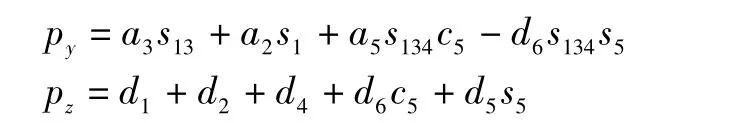
si代表sinθi，ci代表cosθi;sij代表sin(θi+θj)，cij代表cos(θi+θj)，si-j代表sin(θi-θj)，ci-j代表cos (θi-θj);sijk代表sin(θi+θj+θk)，cijk代表cos(θi+θj+θk)。

3 幕墙安装机器人运动学逆解

逆向运动学分析在现实应用中最为常用，它是对机器人进行轨迹控制和路径规划的基础［4］。在对机器人进行运动控制时，需要根据末端的目标位置和姿态，求出机器人各个关节的变量，这就是机器人运动学逆解。由于机器人运动学方程是非线性方程组，建立通用的机器人反解算法非常困难。目前，求解机器人运动学反解的方法大致可以分为数值法、几何法和代数法［5］。

经比较，幕墙安装机器人运动学逆运算采用Paul反变换求解更为简单，其求解步骤为:

(1)建立机器人运动学方程

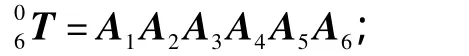
(2)利用 (A1)-1左乘运动学方程，得

(A1)T=A2A3A4A5A6，求解关节变量1;

(3)顺次利用逆矩阵左乘机器人运动学方程，多次运用矩阵的加法、乘法和三角代换依次求出各个关节的变量。

如果幕墙安装机器人的期望位姿为:

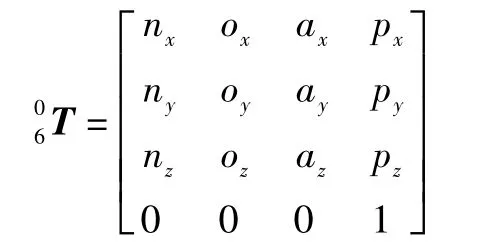
求各个变换矩阵的逆矩阵得到:

由于关节2、3、4相互平行，用 (A1)-1左乘运动学方程、(A6)-1(A5)-1右乘运动学方程得:

于是得到:

取式中第3行第3列元素相等得到

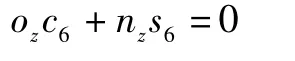
取式中第3行第1列元素相等得到:

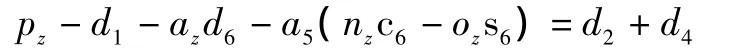
进而求得:

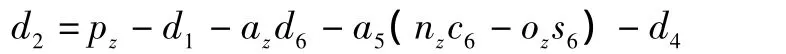
用 (A1)-1左乘运动学方程、(A6)-1(A5)-1(A4)-1右乘运动学方程得:

取式中第3行第2列元素相等得到:

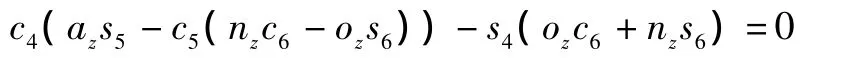
进而求得:

用 (A6)-1(A5)-1(A4)-1右乘运动学方程得:

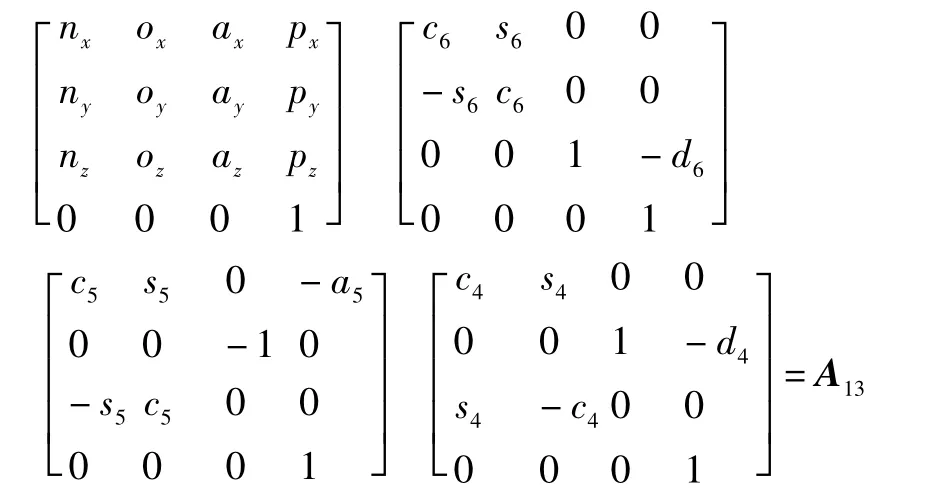
取式中第1行第1列元素相等得到:

取式中第1行第4列元素相等得到:

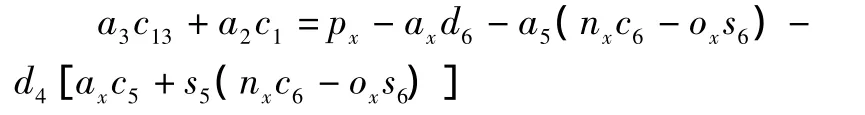
综合以上两式可求得:

该幕墙安装机器人最多可能存在8组解，其中由于关节活动范围的限制，有些解是不符合实际的。除此之外剩余的解应按最短行程的准则选取最优解，即要求每个关节的移动量最小，由于该机器人属于串联机器人，因此适宜采用加权处理，遵循“多移动小关节，少移动大关节”的原则［6］。

4 幕墙安装机器人工作空间分析

对工业机器人的工作空间分析很多国内外学者提出了许多研究方法，大体可以概括为以下3种:解析法、图解法以及数值法。

解析法是由数学推导的方法计算出机器人的工作空间，常用的有两种方法:一是由包络理论确定机器人工作空间;二是图解法，利用几何作图的方法求得机器人工作空间，这种表示方法比较直观而且易于理解，但受机器人自由度的限制。由于目前电子计算机编程和计算能力的迅猛发展，利用数值法求解机器人工作空间显得极其简单，蒙特卡洛 (Monte Carlo)方法是较常用的数值方法之一，首先生成n个随机变量作为关节的输入，然后根据运动学方程算得机器人末端位姿［7］。由于Monte Carlo方法是间隔取值，而且得到的末端的点是离散的，因此通过该方法得到的机器人工作空间与理论工作空间存在误差。

蒙特卡洛方法的步骤如下:

(1)求解机器人运动学方程，得到机器人末端位姿。

(2)机器人的每个关节变量都有自己的取值范围，将每个关节的取值范围均匀的选取n个随机数。例如，机器人的第一关节θ1，首先在0—1范围内生成n个随机数，以α1，…，αn表示，然后根据θ1的取值范围有机器人的其他关节变量做同样处理。

(3)将上一步得到的机器人各关节变量的n组数值代入到第一步求解的运动学方程中去，即可以得到机器人各关节变量和机器人末端相对于基座坐标的一一映射。由机器人末端执行器所达到的这些随机点就构成了机器人工作空间的云图。

利用LabVIEW的计算仿真和绘图能力，据Monte Carlo求解机器人工作空间的步骤，首先根据幕墙安装机器人运动学方程，求解运动学正解，得到末端的目标位置坐标。然后利用LabVIEW中的“随机数VI”和“For循环”产生n个大于0小于1的随机数，记作Randk(k=1，2，…，n)，由此每个运动关节产生一个随机步长:

进而得到每个关节的随机值

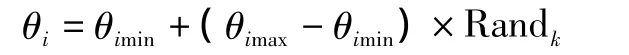
式中:i代表关节，i=1，2，3，4，5，6;Randk代表计算机产生的大于0小于1的随机数，k=1，2，…，n。n代表产生随机数的个数，在这里n取100，即幕墙安装机器人每个关节随机产生100个位姿。

最后将机器人的每个轴所产生的n个随机数值代入到机器人的运动学正解中去，得到机器人末端的位置向量，并将向量端点显示在笛卡尔坐标系中。

运行LabVIEW程序得到幕墙安装机器人工作空间三维点图，如图5所示。

图5 幕墙安装机器人工作空间

5 结论

在深入研究6-DOF机器人运动学的基础上，根据D-H法则，对幕墙安装机器人建立关节坐标系，求解幕墙安装机器人运动学正解和逆解，为机器人的运动控制奠定了基础，并进一步求解了幕墙安装机器人的工作空间，为将来建立机器人的轨迹规划奠定了基础。

［1］白洋，王宏.浅谈高层建筑的发展与特点［J］.黑龙江科技信息，2009(14):260-260.

［2］刘笑含.干挂安装板材机器人系统关键技术研究［D］.天津:河北工业大学，2011:1-5

［3］王颢.高空作业机械在外墙保温施工中的应用［J］.科技与企业，2013(11):228.

［4］KUMAR A，WALDRON K J.The Workspaces of a Mechanical Manipulator.Transaction of the ASME［J］.Journal of mechanical design，1981，103(7):665-672.

［5］NIKU Saeed B.机器人学导论—分析、系统及应用［M］.北京:电子工业出版社，2004.

［6］路甬祥，陈鹰.人机一体化系统与技术——21世纪机械科学的重要发展方向［J］.机械工程学报，1994，30(5):1-6.

［7］楼晓明.机电一体化产品设计问题探析［J］.机电信息，2010(6):109-120.