轻轨隧道循环掘进爆破地震效应研究

王 辉，常中民，阳生权，丁 雄

(1.湖南科技大学 土木工程学院，湘潭 411201；2.中铁十六局集团第三工程有限公司，湖州 313000)



轻轨隧道循环掘进爆破地震效应研究

王 辉1，常中民2，阳生权1，丁 雄1

(1.湖南科技大学 土木工程学院，湘潭 411201；2.中铁十六局集团第三工程有限公司，湖州 313000)

以重庆轨道交通环线冉家坝浅埋轻轨隧道工程为背景，进行循环掘进的地表爆破震动效应试验.通过测量隧道地表不同位置处引起的振动速度波形，研究地表震动特性及爆破地震波的传播和衰减规律.试验研究分析发现，掌子面前后的地表振动速度存在显著地差异，已开挖成形隧道改变了岩体的整体结构，爆破振速存在放大效应，且放大后的爆破振速随距离的增大而减小，用常规的萨道夫公式预测成形隧道地表的振动速度误差较大，而通过编写matlab函数进行数据统计、多元线性回归分析求出广义的爆破震动速度计算公式，预测成形隧道地表振动速度误差较小.所以广义的爆破震动速度公式预测成形隧道地表振动速度值得推广.

爆破震动；衰减规律；回归分析

随着我国城市化建设的发展，城市交通压力与日俱增.以钻爆法为城市地铁隧道循环掘进的主要方法，对加 快城市地铁建设，减缓城市交通起到重要作用.同时，爆破施工产生的爆炸空气冲击波、爆破飞石、爆破噪声，尤其是爆破地震效应对城市复杂环境下建筑物的影响是不能忽视的[1-2].在人口和建筑密集的城市进行爆破开挖，对其爆破振速控制有其严格的要求.因此要求能够准确分析爆破地震波的传播和衰减规律，预测爆破振速，通过爆破优化设计与施工有效的减小爆破振动危害.目前，工程中通常采用式(1)萨道夫斯基公式预测爆破振速的量值[3-5]：

(1)

式中：R为测点到爆破中心的距离(m)；Q为炸药量，齐发爆破取总药量，微差爆破时取最大段装药量(kg)；v为爆破岩石质点振动速度(cm/s);k为与岩石性质、爆破参数和爆破方法有关的场地系数；α为爆破震动衰减系数.

以往工程实际证明，萨道夫斯基公式在平整地形条件下预测地面的爆破振速有较高的精度，但该公式没有考虑已开挖成形隧道对地表振动速度的影响[6].基于这一点认识，也有不少学者对此进行了研究，文献[7]认为浅埋隧道开挖区造成掘进爆破产生的地表震动产生“空洞效应”，成形隧道对岩体整体结构的改变导致地表振速产生放大效应，掘进前方的爆破地震效应可以萨道夫斯基公式进行预测，掘进后方的爆破地震波则不符合这一衰减规律.

上述学者的研究表明，开挖成形隧道对地表爆破振速产生影响，并且产生放大效应，但未对具体衰减规律进行分析.本文通过实测爆破振动数据发现，开挖成形隧道对地表爆破振动速度的确产生放大效应，同时爆破振速也随着距离的增加而减小，也应满足某一衰减规律.因此通过编写matlab函数进行数据统计、回归分析求出广义的爆破震动速度计算公式，预测开挖成形隧道地表速度，与实测爆破振速吻合较好.

1 工程实例

1.1 工程概况

冉家坝施工通道轻轨隧道位于重庆市渝北区境内，全长483 m，标准断面净宽6 m，净高5.5 m,埋深16～24 m，该段隧道属于浅埋隧道，采用钻爆法施工.隧道围压属于III、IV级，岩性以砂岩、砂质泥岩为主.该段靠近重庆广电大厦、重庆工商局、杨子江商务小区等重点需要保护的高层建筑物，同时下穿已建好的冉家坝轻轨站，因此对爆破振动控制要求严格.

1.2 试验方案与量测方法

由于隧道开挖成形后，掌子面前后的岩体结构、地应力重新分布，爆破条件发生大的变化，为了对比掌子面前后地表振动速度的传播和衰减规律.现场以掘进掌子面为中心，在隧道轴线地表对称布置振动监测点，测点按一定间距布置，正反两个方向各布置5个测点，掌子面布置一个测点，如图1所示.

图1 爆破振动测点的平面布置图

振动测量系统由拾振器、记录仪和笔记本电脑组成.采用四川拓普测控科技有限公司生产的UBOX5016数据采集设备及配套软件进行数据采集.现场测试安装传感器时，采用生石膏粉加适量的水调节成浆糊状，将传感器粘结在测点上，过几分钟石膏凝固达到传感器与地面刚性连接后，保持垂直速度传感器与水平面垂直，水平径向速度传感器与水平面平行，水平切向速度传感器在水平面内与水平径向速度传感器垂直，构成一个关于爆心的3维直角坐标系，可以进行爆破震动测试.

1.3 数据分析

为了优化爆破方案，指导爆破施工，控制爆破地震效应对周围密集的高层建筑的影响.在隧道施工初期，通过对爆破震动进行了监测，了解现场条件下的爆破震动传播与衰减规律，计算出场地影响系数k值和衰减指数α.初期爆破震动监测数据见表1.各测点振动速度的变化特征见图2.

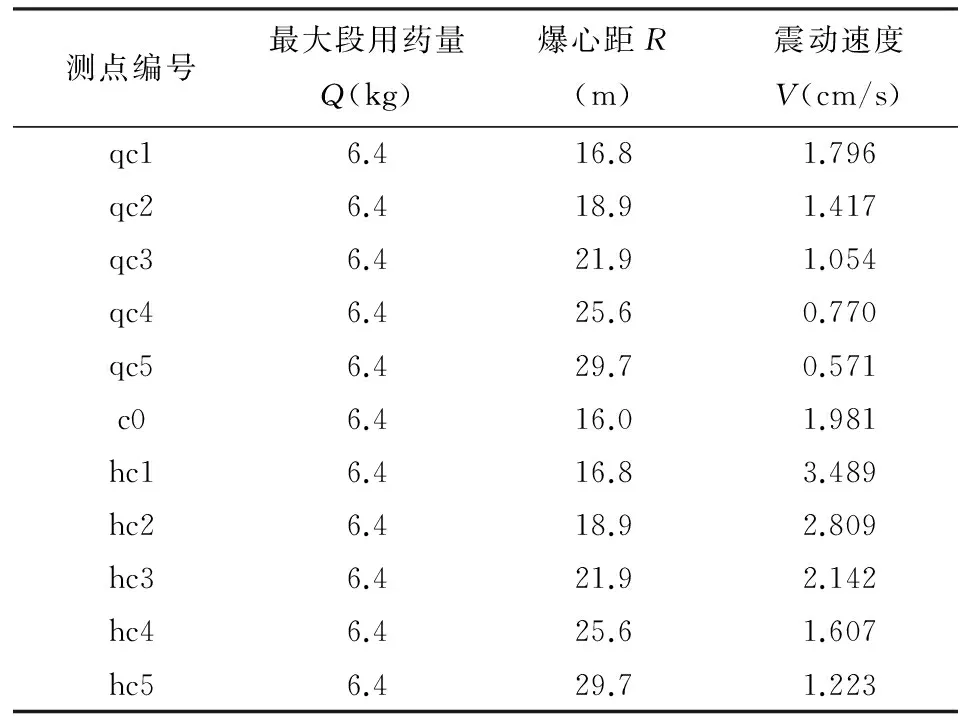
表1 钻爆初期施工爆破震动监测数据

图2 钻爆初期地表各测点振动速度的变化特征

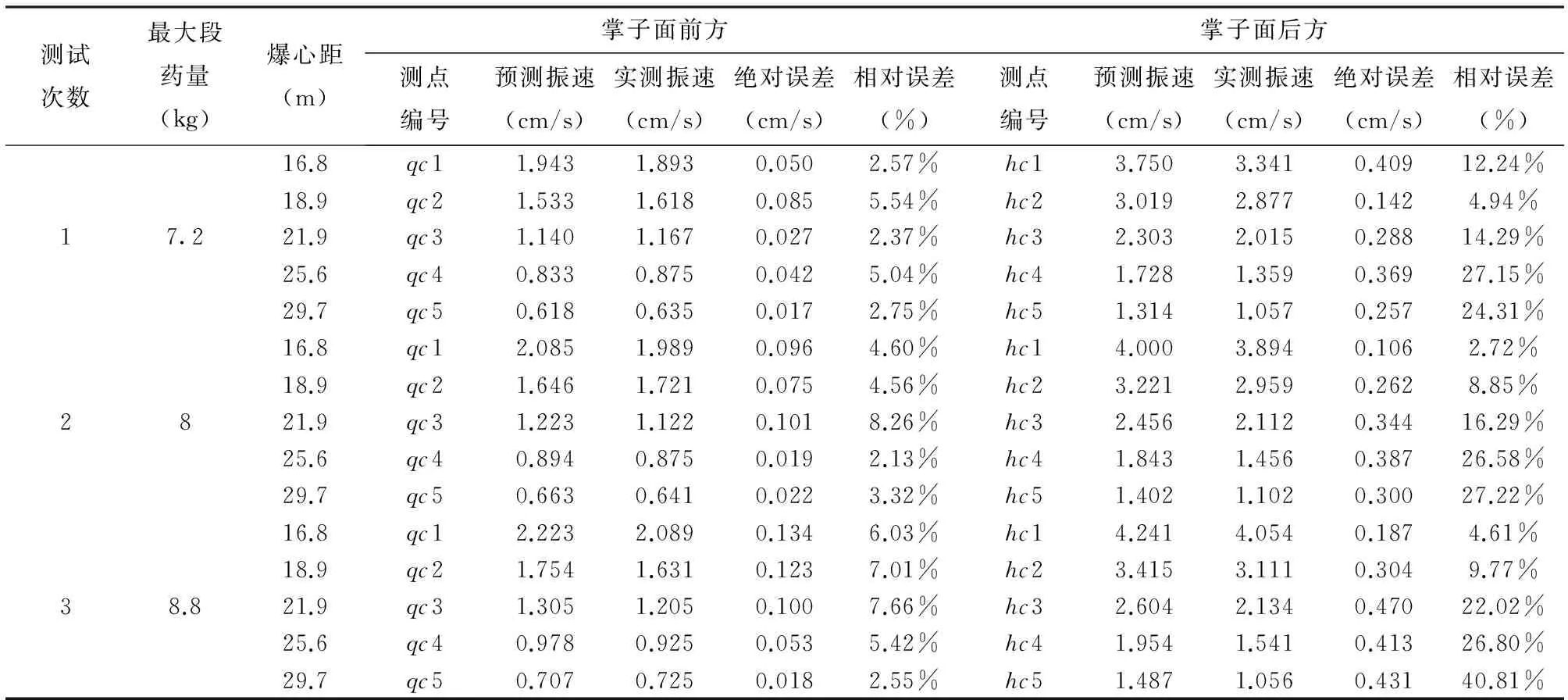
随着钻爆施工的推进，用萨道夫斯基公式预测爆破中期爆破震动速度并与实测数据对比,由于篇幅原因只列部分数据，见表2.例举第4次测点振动速度的变化特征见图3.

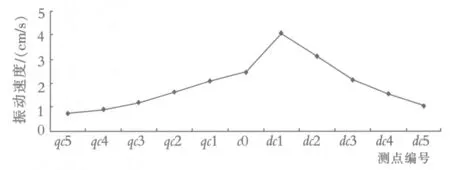
图3 钻爆中期地表各测点振动速度的变化特征

测试次数最大段药量(kg)爆心距(m)掌子面前方掌子面后方测点编号预测振速(cm/s)实测振速(cm/s)绝对误差(cm/s)相对误差(%)测点编号预测振速(cm/s)实测振速(cm/s)绝对误差(cm/s)相对误差(%)16.8qc11.9431.8930.0502.57%hc13.7503.3410.40912.24%18.9qc21.5331.6180.0855.54%hc23.0192.8770.1424.94%17.221.9qc31.1401.1670.0272.37%hc32.3032.0150.28814.29%25.6qc40.8330.8750.0425.04%hc41.7281.3590.36927.15%29.7qc50.6180.6350.0172.75%hc51.3141.0570.25724.31%16.8qc12.0851.9890.0964.60%hc14.0003.8940.1062.72%18.9qc21.6461.7210.0754.56%hc23.2212.9590.2628.85%2821.9qc31.2231.1220.1018.26%hc32.4562.1120.34416.29%25.6qc40.8940.8750.0192.13%hc41.8431.4560.38726.58%29.7qc50.6630.6410.0223.32%hc51.4021.1020.30027.22%16.8qc12.2232.0890.1346.03%hc14.2414.0540.1874.61%18.9qc21.7541.6310.1237.01%hc23.4153.1110.3049.77%38.821.9qc31.3051.2050.1007.66%hc32.6042.1340.47022.02%25.6qc40.9780.9250.0535.42%hc41.9541.5410.41326.80%29.7qc50.7070.7250.0182.55%hc51.4871.0560.43140.81%

通过表2数据分析可得，对于掌子面前方地表爆破振速用萨道夫斯基预测与实际测得比较吻合，其绝对误差和相对误差均相对较小.而对已开挖成形隧道地表震动速度用萨道夫斯基预测与实测相差甚远，其绝对误差和相对误差均较大.由图2、图3可以看出地表测点振动速度的变化特征：掌子面前后爆破振速存在明显差异，掌子面后方地表的爆破振速明显比掌子面前方地表的爆破振动速度大，且掌子面后方地表放大后的爆破振速也随着距离的增加而衰减，文献[7]图五、图六也反应了类似的变化，掌子面后方爆破振速放大后同样类似于掌子面前方的爆破振动衰减曲线.

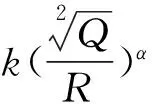
对表2中开挖成形地表爆破震动数据进行多元回归分析，在matlab的M函数中输入监测样本数据(Q，R，V)进行多元线性回归后，计算机输出结果b=【 2.9098，0.4556 ，-2.2375】，也就得出公式中的k、α、β值， 分别为k= 821.456 ；α= 0.4556 ；β= -2.2375 ；由此可知，本隧道已开挖成形隧道地表爆破震动传播的广义衰减公式为：v=821.456·Q0.4556R-2.2375.运用此公式与萨道夫斯基公式预测开挖成形隧道地表的爆破振速进行比较如表3所示.

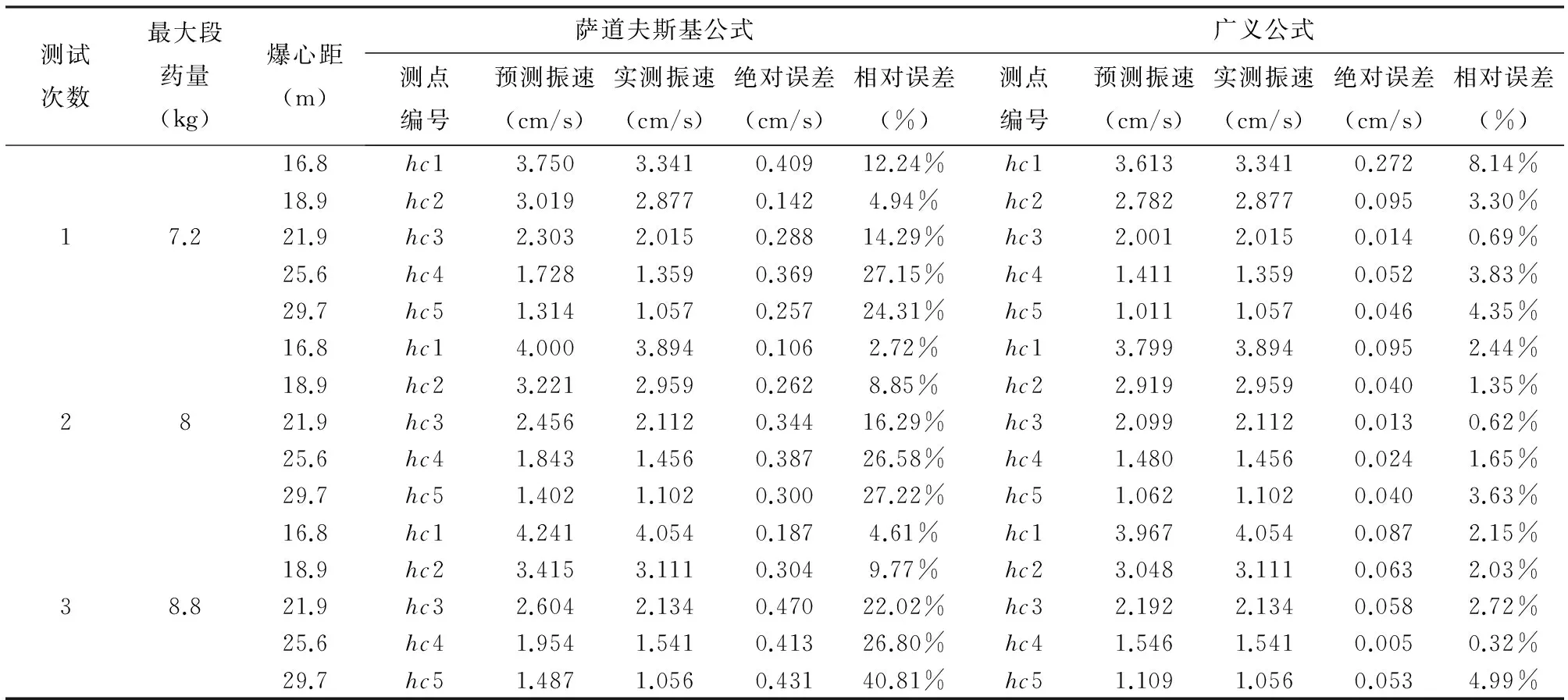
表3 公式预测与实测数据的比较及误差分析

2 结 论

(1)掌子面隧道后方地表爆破振速明显大于掌子面隧道前方地表爆破振速，已开挖成形隧道地表的爆破震动确实有放大效应，因此在对城市建筑物爆破地震效应控制时，要以掌子面后方测得的爆破振速作为控制标准，最大限度的保护建筑物的安全.

(2)轻轨浅埋隧道掘进前方用萨道夫斯基公式预测爆破振速与实测振速吻合较好，对冉家坝隧道前方的地震动衰减参数为k=150.3；α=2.01.而掘进后方的爆破震动用萨道夫斯基公式预测误差较大.

(3)轻轨浅埋隧道掘进后方地表爆破振速有放大效应，同时爆破振速也会随着距离的增加而减小，运用编写matlab函数进行数据统计、回归分析求出广义的爆破震动速度计算公式预测其爆破公式与实测振速相应吻合.其相应系数为k=821.456；α=0.4556；β=-2.2375.用广义衰减公式预测隧道掘进后方地表爆破振速误差较小.

[1] 沈秀峰.地铁爆破施工对建筑物的微振动影响分析[D].大连交通大学2012.

[2] 高尔新,杨树仁.爆破工程[M].徐州市:中国矿业大学出版社,1999.

[3] 吕 涛,石永强,黄 城,等.非线性回归法求解爆破振动速度衰减公式参数[J].岩土力学,2007,28(9):1871-1878.

[4] 张世雄,杨树亮,尹家国,等.预测爆破波振动强度的经验公式及其在采矿中的应用[J].爆破,2000,17(3):13- 17.

[5] 张继春,彭琼芳.岩体爆破地震波衰减规律的现场试验与分析[J].辽宁工程技术大学学报(自然科学版),2001, 20(4):399-401.

[6] 唐 海,李海波. 反映高程放大效应的爆破振动公式研究[J]. 岩土力学,2011(3):820-825.

[7] 张继春,曹孝君,郑爽英,郭学彬.浅埋隧道掘进爆破的地表震动效应试验研究[J].岩石力学与工程学报,2005(22).24(22):4158-4163.

[8] 罗 正,陈寿如,王恒富,邓重阳. 广义的爆破震动速度计算公式及其应用[J]. 采矿技术,2007(3).

Experimental Study on Blasting Seismic Effect Resulting from Circular Driving in Light Rail Tunnel

WANG Hui1，CHANG Zhong-min2，YANG Sheng-quan1，DING Xiong1

(1.College of Civil Engineering，Hunan University of Science and Technology， Xiangtan 411201， China；2.China Railway 16th Bureau Group Third Engineering Co., LTD.Huzhou 313000， China)

Taking the project of Ranjiaba shallow light rail tunnel of chongqing rail transit circle as the background, the field experiments of blasting vibration effects of the ground in circular driving have been done. Based on the measurement of the waveforms of the vibration velocity in different distances on the ground, the vibration characterist of the ground and the propagation and attenuation laws of lasting seismic wave are studied. The research tests and analysis show that the ground vibration velocity of in the front of and behind the tunnel face exists significant differences. The rock mass of the entire structure has been changed for the tunnel has been forming result from excavating. Blasting vibration velocity is magnified and the blasting vibration velocity decreases with the increase of distance. Predicting the forming tunnel of the ground blasting vibration velocity with sadov's formula has a larger error.And by writing matlab function for data statistics and multivariate linear regression analysis to find the general formula of blasting vibration velocity, the forming tunnel of the groun vibration velocity is predicted with a small error. So using the generalized tunnel blasting vibration velocity formula to predict the forming tunnel of the ground vibration velocity is worth promoting.

blasting vibration;attenuation law;regression analysis

2014-09-01

湖南省高校产业化培育项目(13CY013).

王 辉(1989-)，男，硕士研究生，研究方向：岩土工程.

TD235

A

1671-119X(2015)01-0076-04