EMD在扭转振动分析中的应用研究*

， ，

(广东海洋大学，广东 湛江 524088)

0 引言

柴油机气缸内气体压力周期性变化，运动部件重力及其往复惯性力周期性变化，接受功率的部件不能均匀地吸收扭振所产生的激励等可能会导致船用柴油机曲轴、传动轴以及凸轮轴疲劳折损。如果扭振幅值过大将可能会激起柴油机机架与齿轮箱的横向振动，引起机舱构件的局部振动以及上层建筑及船体振动。监测船舶轴系的固有频率和船上有关的激励频率之间是否出现共振，特别是监测船舶推进轴系的低频振动显得尤为重要。

本文通过数值仿真实验，明确固有模态函数与系统振动频率的对应关系，即一个固有模态函数与系统中某一个频率不是一一对应的。通过对扭转振动进行测试分析，探讨了经验模态分解在推进轴系扭转振动分析中的应用。

1 经验模态分解与希尔伯特黄变换

经验模态分解(Empirical Mode Decomposition, EMD)计算数据的上下包络平均值，将包络平均值作为瞬时平均值。用原始信号减去瞬时平均值，得到新的数据，判断新数据是否满足固有模态函数(Intrinsic Mode Function, IMF)的定义，如果新数据是固有模态函数，就从原始信号中减去新数据，得到残留数据，直到残留数据少于2个极值点，终止分解运算[1-2]。分解过程见公式1。

如果一个函数的极值点数目和过零点数目相等或者最多相差1个；而且这个函数在任意点，由局部极大值和局部极小值点构成的2条包络线平均值为0。那么，这个函数称为固有模态函数[2]。

EMD方法是一个筛选过程,采用信号局部极值和紧随其后的样条函数拟合来近似分解[3]。EMD是一个数据驱动和自适应的过程[4]。每个线性或非线性模式将具有相同数量的极值点和零交叉点,每个模式都独立于其他模式[5-6]。

x(t)=imf1(t)+r1(t)

=imf1(t)+imf2(t)+r2(t)

=imf1(t)+imf2(t)+imf3(t)+r3(t)

(1)

⋮

希尔伯特黄变换(Hilbert-Huang Transform, HHT)是将所要分析的数据分解为IMF后，再对每一个IMF做HHT，从而正确地获得信号的瞬时频率。瞬时频率定义为瞬时相位的一阶导数[7]。

数据x(t)的希尔伯特黄变换定义如下：

(2)

重构信号z(t)为解析信号，见公式(3)。

z(t)=x(t)+jy(t)

=a(t)eiθ(t)

(3)

那么，瞬时幅值见公式(4)。

(4)

瞬时相位见公式(5)。

(5)

瞬时频率见公式(6)。

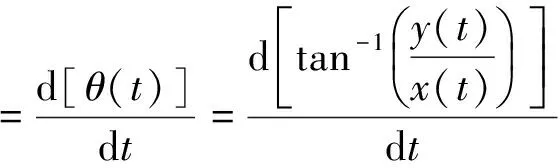
(6)

由于只能对有限个样本进行计算，当时域截断时，传统的FFT，不可避免地产生能量泄漏，谱峰值变小，从而产生幅值误差[8]。

与其他数学变换(如快速傅立叶变换(FFT)、小波变换(WAVELET)等)不同，希尔伯特黄变换是一种应用在数据上的算法，而非理论工具，其处理对象是非稳态与非线性信号。这种基本上符合物理意义的分解，是其他变换难以实现的[1]。HHT变换可以跟踪瞬时频率的变化,在处理变压器振动信号时，HHT具有独特的优势[7]。

2 数值仿真实验

信号由不同频率的正弦波组成，并含有随机噪声。

signal1=sin(2*pi*10*t)+sin(2*pi*50*t)+sin(2*pi*100*t)+sin(2*pi*150*t)+sin(2*pi*200*t)+sin(2*pi*250*t)+sin(2*pi*300*t)+sin(2*pi*350*t)+sin(2*pi*400*t)+sin(2*pi*450*t)+0.1*randn(1, length(t));

信号signal1的傅立叶变换见图1。在频谱图上，10个不同频率明显被分辨出来。

图1 signal1与其傅立叶谱

信号signal1的EMD分解见图2，从图中可以看出，第一个IMF的频谱只分辨出9个频率，第二个IMF，第三个IMF虽然有表征，但未能明显表征10 Hz频率。EMD对系统内不同频率振动能量差别不大时，频率特征识别能力较差。

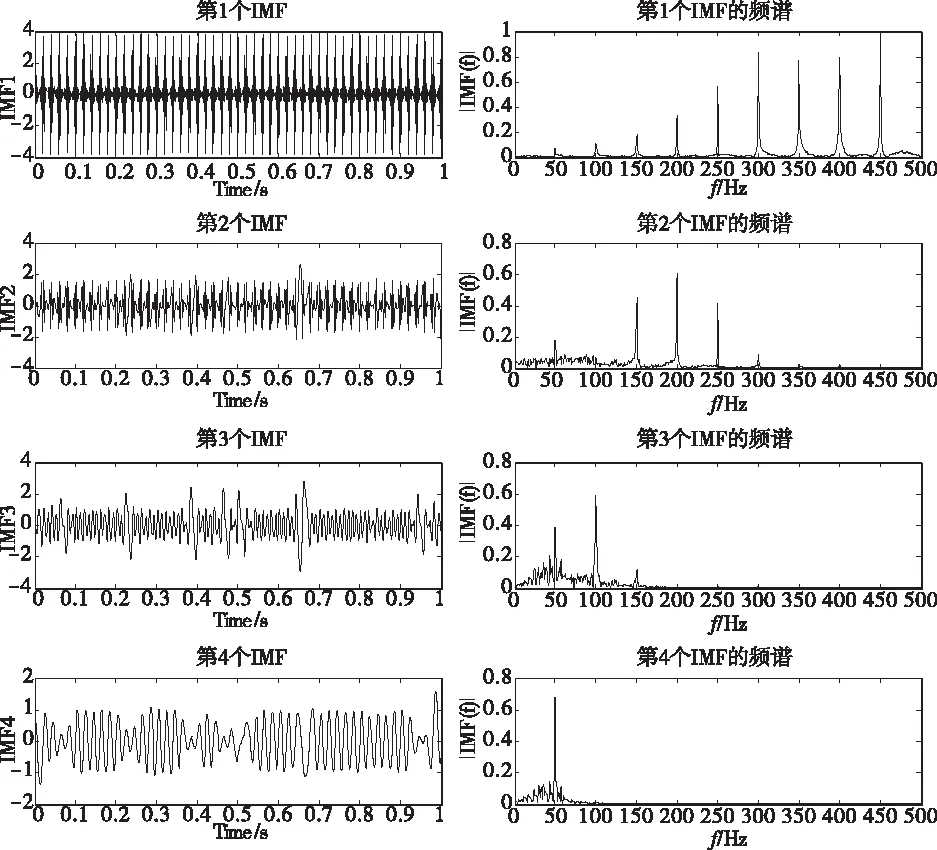
图2 signal1的IMF与其频谱

另一方面,在采集的数据集上，固有模态函数(IMF)分量不能自动保证有一个定义明确的物理意义[4]，因此采用EMD分解IMF分量前，需要仔细选择所采集数据的尺度，以便有明确的解释。

如果把含有随机噪声的信号更改如下：

signal2=10*sin(2*pi*10*t)+2*sin(2*pi*50*t)+sin(2*pi*100*t)+20*sin(2*pi*150*t)+8*sin(2*pi*200*t)+30*sin(2*pi*250*t)+20*sin(2*pi*300*t)+sin(2*pi*350*t)+8*sin(2*pi*400*t)+20*sin(2*pi*450*t)+0.1*randn(1, length(t))

不同于信号signal1，信号signal2的各频率成分的振幅(或振动能量)相差比较大。在信号signal2的快速傅立叶变换频谱图(图3)上，8个不同频率较明显地被分辨出来,但100 Hz，350 Hz不能明显表征。

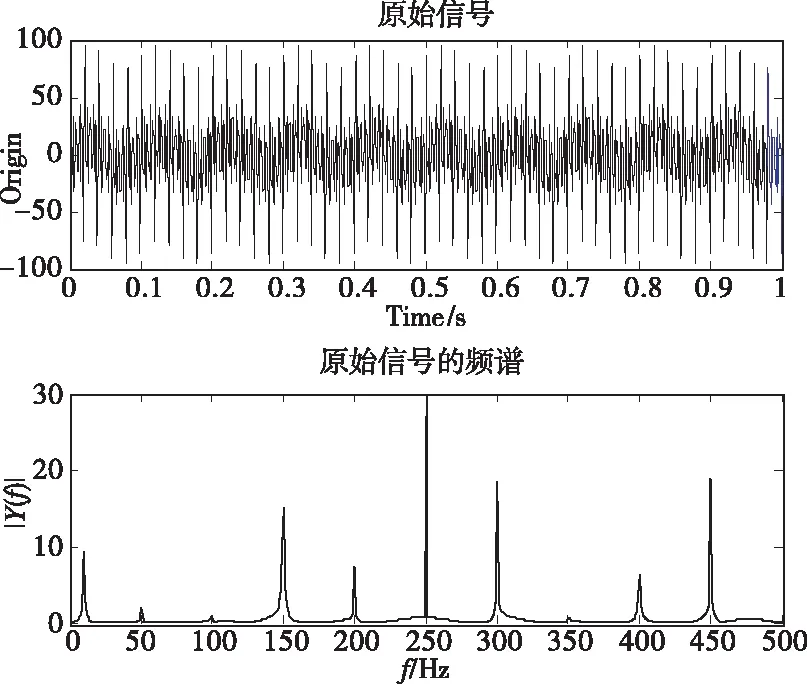
图3 signal2与其傅立叶谱

信号signal2的EMD分解见图4，从图4中可以看出，第一个IMF的频谱只分辨出9个频率，但第二个IMF对100 Hz频率做了补充表征，第三个IMF对50 Hz频率做了补充表征，第四个IMF对10 Hz频率做了补充表征。经多次数值分析实验，EMD对各频率振动能量差别大的系统，有较好的频率特征识别能力。

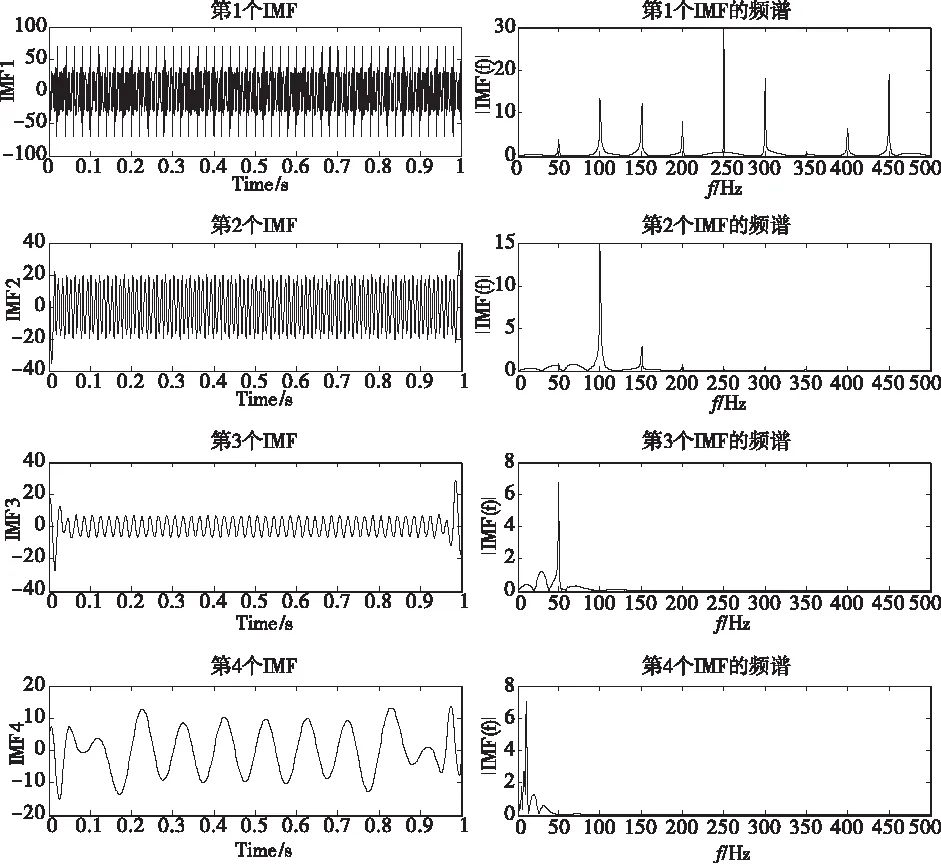
图4 signal2的IMF与其频谱

如果把不同频率的振幅再加大，把含有随机噪声的信号更改如下：

signal3=20*sin(2*pi*10*t)+0.5*sin(2*pi*50*t)+10*sin(2*pi*100*t)+15*sin(2*pi*150*t)+10*sin(2*pi*200*t)+20*sin(2*pi*250*t)+0.1*sin(2*pi*300*t)+20*sin(2*pi*350*t)+10*sin(2*pi*400*t)+20*sin(2*pi*450*t)+0.1*randn(1, length(t))

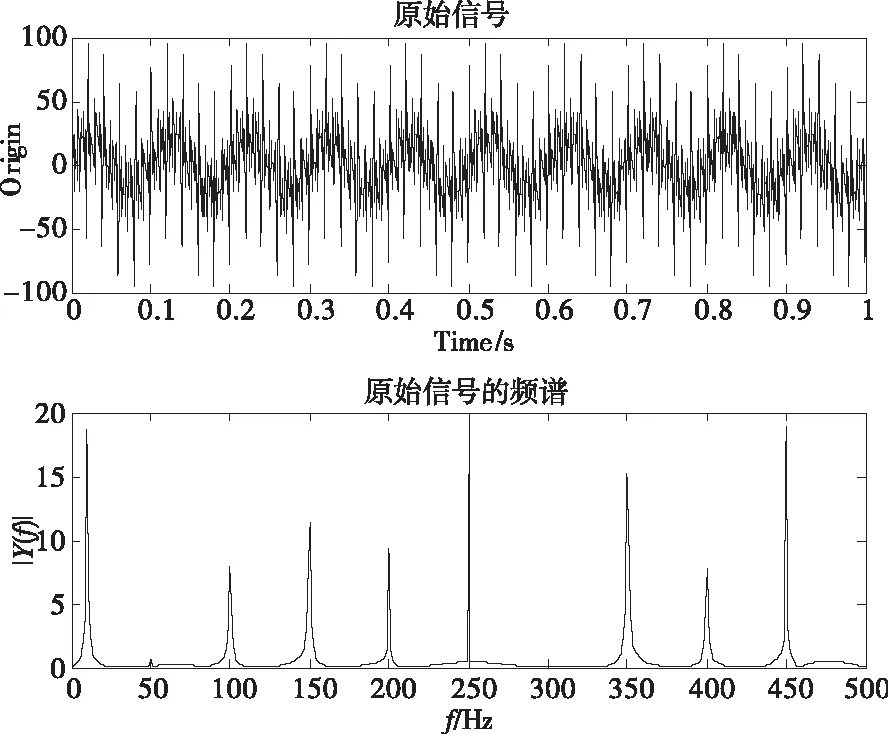
图5 signal3与其傅立叶谱

从图5与图6可以看出，快速傅立叶变换对50 Hz,300 Hz没有明显表征。而EMD分解对100 Hz,50 Hz在IMF3做了补充表征，对10 Hz在IMF4上做了补充表征。但300 Hz频率补充表征不是很明显。总之，EMD分解宽带信号时，是从高频到低频, 而不是从高能量到低能量[3]。这个特征使得EMD能够分解出低频弱能量信号[3]。

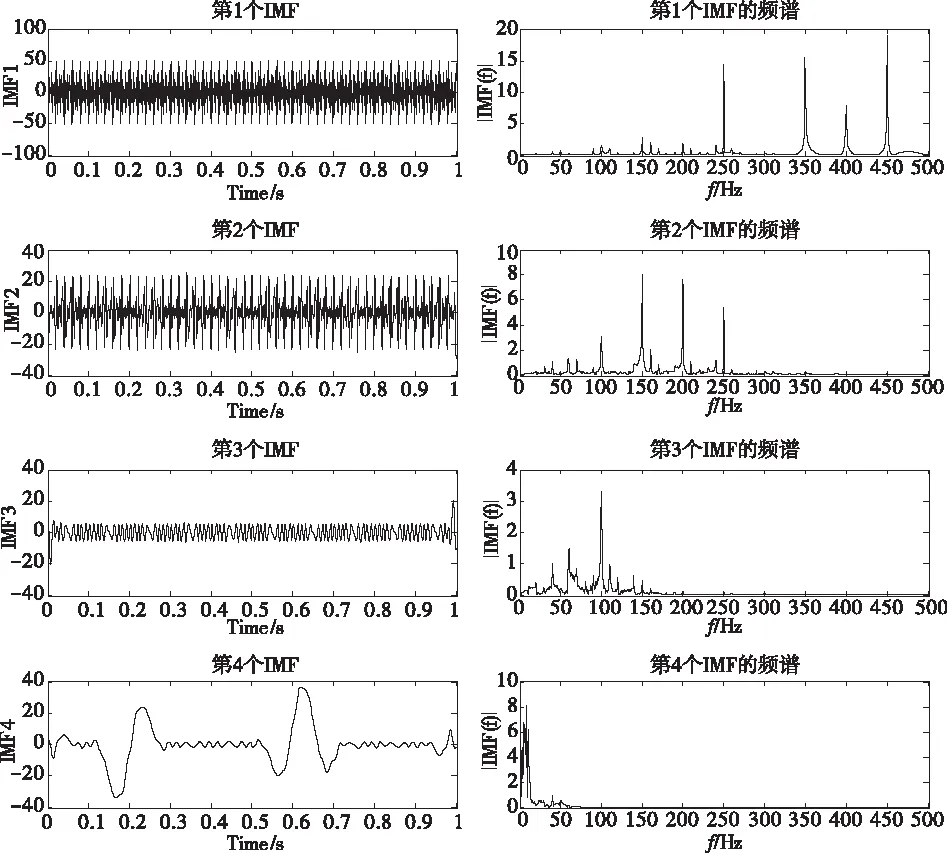
图6 signal3的IMF与其频谱

如果信号更改如下：

a=2*t+3;

signal4=a.*sin(2*pi*200*t+pi*t)

信号signal4是幅值相位随时间变化的信号，从图7、图8中可以看出，快速傅立叶变换与EMD分解都能明显地表征200 Hz频率这个单一频率。

图7 signal4与其傅立叶谱

图8 signal4的IMF与其频谱

如果信号更改如下：

a=2*t+3;

signal5=sin(2*pi*200*a.*t+pi*t);

信号signal5是频率、相位随时间变化的，从图9、图10中可以看出，EMD分解能较好地表征低频弱能量信号。

图9 signal5与其傅立叶谱

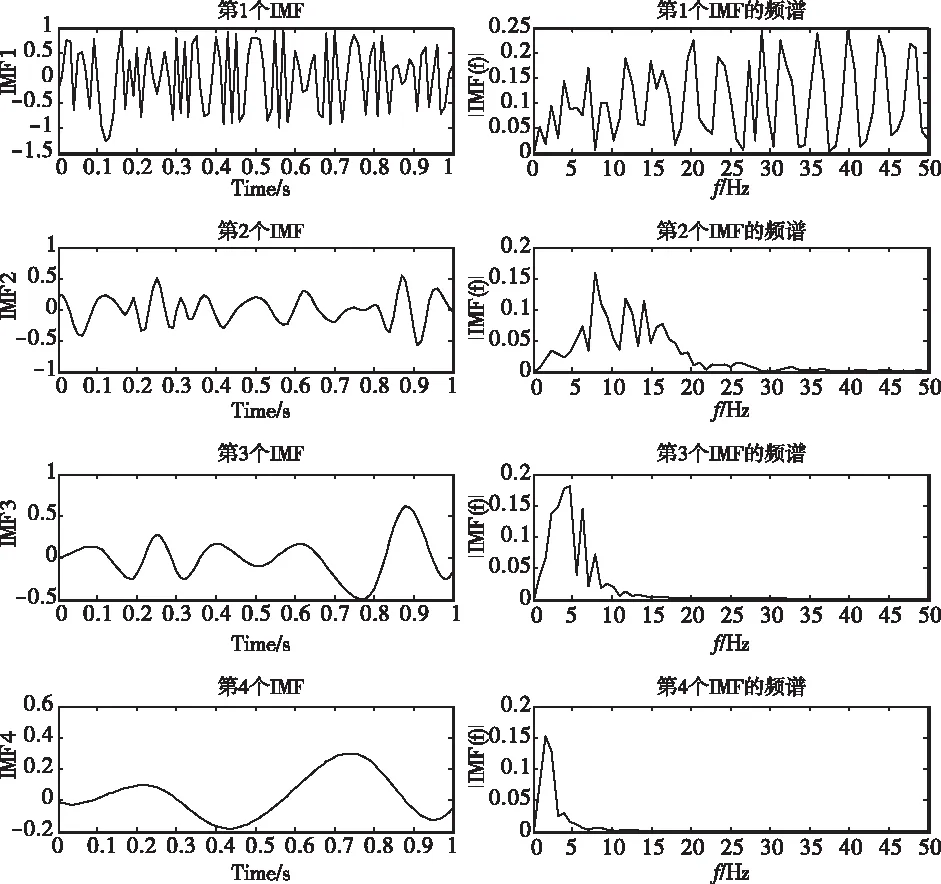
图10 signal5的IMF与其频谱

EMD分解的IMF能量和原信号的能量(可能)是不完全相等[8]。FFT谱和原信号的能量是相等的。从EMD的定义与数值分析实验表明，一个固有模态函数与系统中某一个频率不是一一对应。对于不复杂的系统，一般情况下，前4阶固有模态函数基本上能够表征系统的模态。

EMD分解后的固有模态函数是不等带宽的，所以，EMD分解适合非线性信号分析[6]。

3 实测扭振数据分析

电机型号：Y2-90S-4，电机功率：1.1 kW，频率50 Hz,额定转速：1 440 r/min,轴直径：φ30，中间齿轮齿数：60。

实验测试仪器采用ANZT双通道扭振分析记录仪，扭角测试：量程：0-10°(峰值)；分辨率：1毫度。测试平台见图11。

图11 实验测试台

实测数据及其傅立叶谱，见图12。

扭振信号的频率成分主要是由低频的滚振成分和与转速相关的各谐次成分组成。从图12、图13实测的数据来看，在启动过程中，扭振信号是一组低频的变频信号。

图12 实测数据及其傅立叶谱

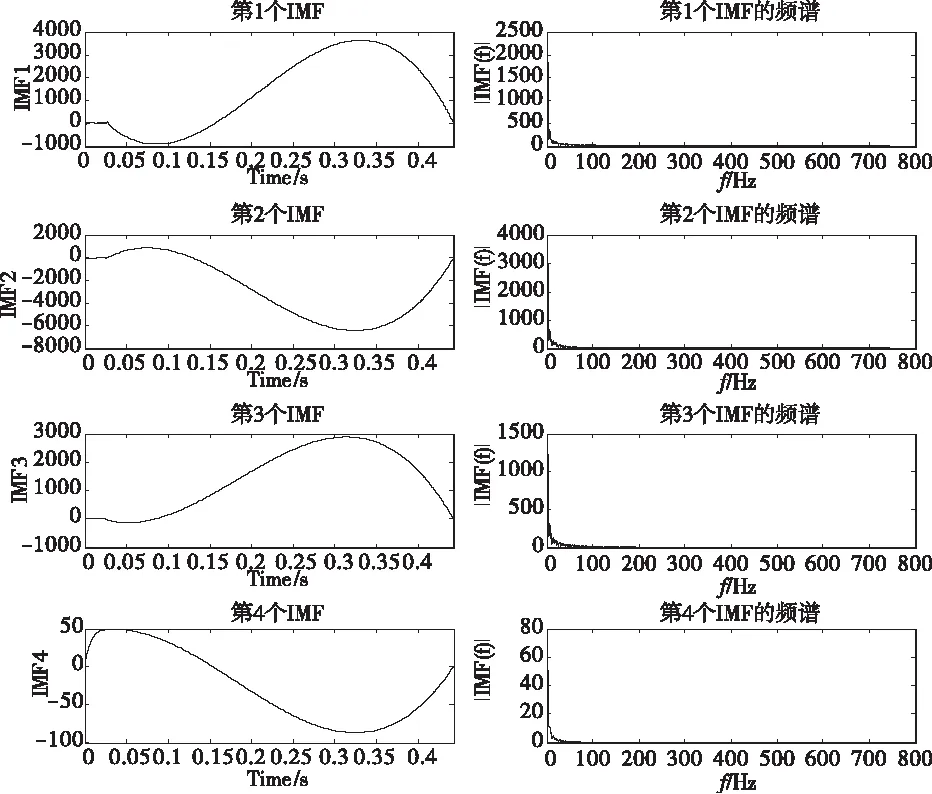
图13 实测数据的IMF与其频谱

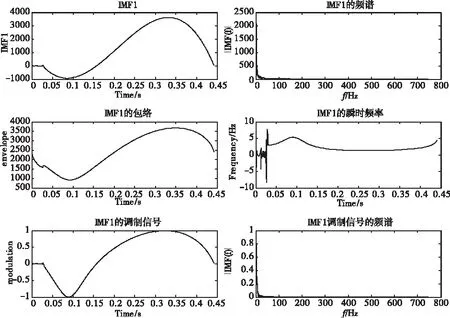
图14 实测数据IMF1的瞬时频率

从图14中看出，所测扭振信号频谱成分复杂，与频率变化(非平稳)的信号有类似的谱图，低频成份较多。与实际相比，FFT变换仅能够明晰趋势的变化，不能反映启动工况下扭振信号的实际物理意义。而EMD，除去其端点效应，第一IMF最大扭角达到350毫度，第二IMF最大扭角达到210毫度，第三个IMF最大扭角达到10毫度，与实测数据基本相同，基本上表征了扭振实际过程的特性。从图13实测数据IMF1的瞬时频率中可以看出，启动过程中，转速达到200 r/min以上后，扭振频率没有太大变化。

4 结论

EMD分解适合非线性与非平稳信号，所分解的固有模态函数与系统中的固有频率不是一一对应的，通常情况下，前4阶固有模态函数基本上能够表征系统的模态。

在传统的稳态扭振信号处理中，首先采集各稳态转速下扭振信号；然后提取各谐次幅值的谱分析；最后对各稳态转速下各谐次幅值进行整理，并用多项式曲线拟合得到转速振幅图。

本文由于采用ANZT双通道扭振分析记录仪，得到扭振数据并将数据导入MATLAB，通过编程分析，验证了EMD对扭振测试数据有较好的分析能力。

[1] Jian Zhang, Ruqiang, et al. Performance enhancement of ensemble empirical mode decomposition[J]. Mechanical System and Signal Processing, 24(2010)：2104-2123

[2] Y. Huang, C. J. Yan, et al. On the difference between empirical mode decomposition and Hilbert vibration decomposition for earthquake motion records[R].15 (World Conference On Earthquake Engineering ) WCEE LISBOA 2012

[3] C. W. Poon, and C. C. Chang. Identification of nonlinear elastic structures using empirical mode decomposition and nonlinear normal modes[J]. Smart Structures and Systems, Vol. 3, No. 2 (2007)

[4] Hui Li, Yuping Zhang, et al. Hilbert-Huang transform and marginal spectrum for detection and diagnosis of localized defects in roller bearings[J]. Journal of Mechanical Science and Technology, 23 (2009)：291-301

[5] Yujun Li, Peter W. Tse, et al. EMD-based fault diagnosis for abnormal clearance between contacting components in a diesel engine. Mechanical Systems and Signal Processing[J].24 (2010)：193-210

[6] Hiralal Khatri, Kenneth Ranney, et al.. Empirical mode decomposition based features for diagnosis and prognostics of systems[J]. Sensors and Electron Devices Directorate. ARL. Army Research Laboratory. Adelphi, MD 20783-1197

[7] Shuyou WU, Weiguo HUANG, et al. extracting power transformer vibration features by a time-scale-frequency analysis method[J]. J. Electromagnetic Analysis & Applications, 2010(2)31-38

[8] 刘庆敏，扬午阳，等. 基于经验模态分解的地震相分析技术[J].北京：石油地球物理勘探，2010,45(增刊1)：145-149