某型无人直升机结构振动可靠性分析及研究

，

(中国人民解放军总参谋部第六十研究所，江苏 南京 210016)

0 引言

无人直升机作为一种特殊的航空飞行器，近几年来在军事领域和关键民用领域得到越来越广泛的应用和重视。相对于固定翼无人机来说,无人直升机旋翼及尾旋翼系统对机体施加的周期性激励是无人直升机产生强烈振动的主要原因，而且过高的振动水平会引起机体结构的疲劳破坏，影响机载设备的正常工作，严重影响了无人直升机的飞行品质[1,2]。随着科学技术的发展和无人直升机系统对振动环境要求的越来越高，无人直升机机体的振动水平已经成为评定无人直升机性能的一项重要指标，所以进行机体减振设计以及振动可靠性研究十分必要。

一般的振动分析是建立在动力学的基础之上的，简单的依靠机械振动理论来进行机械结构设计，由于这种设计理论的基本出发点是把所有的设计变量(如尺寸、材料参数等设计变量)看成是确定性的量，从而使设计的产品无法提供结构的可靠性水平。本文在一般的无人直升机结构振动设计与分析的基础上，考虑了结构设计变量随机性情况，提出了无人直升机结构振动可靠性分析方法及推导了相应的振动可靠度计算公式。最后，以某型无人直升机为例说明了所提方法的合理性及推导公式的正确性。

1 振动可靠性分析

常规振动可靠性分析是将ω激j∈[(1-a)ω固i，(1+a)ω固i](其中的a根据结构振动特性确定，一般地a取0～0.3[5])作为振动可靠性设计准则，即激振频率落在该区域内时，就确定产生不可接受的振动响应，溢出该区域即为振动安全，见图1所示。

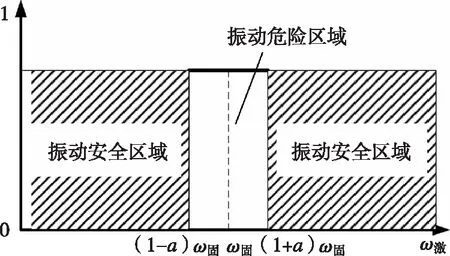
图1 振动安全和危险区域示意图

根据振动理论和结构固有频率特点可知，多自由度结构各阶固有频率是相互独立的，而且这些固有频率和多个激振频率也是相互独立的。因此，结构振动可靠性分析时，考虑各种主客观因素，将影响结构固有频率和激振频率的各因素当作服从一定分布的随机变量来看[3-5]。用g(ω固i)(i=1，2，…，n)来表示结构前n阶固有频率分布的概率密度函数，用f(ω激j)(j=1，2，…，m)表示结构m个激振频率分布的概率密度函数。此处的概率密度函数g和f可以是正态分布、对数正态分布、Weibull分布等不同的概率分布形式，对于简单结构系统，可以用根据结构设计变量分布形式显式解出。根据常规振动可靠性理论，结构m个激振频率与第n阶固有频率之间振动安全的可靠度可以由以下公式给出。

1.1 单自由度单频激励系统

单频激励和系统固有频率之间发生不可接受的振动响应的概率为：

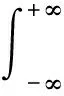
(1)

振动安全的概率为：

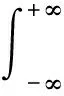
(2)

1.2 多自由度单频激励系统

单频激励和多系统第i阶固有频率之间发生不可接受的振动响应的概率为：

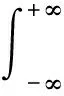
(3)

振动安全的概率为：

Ri=1-Pi

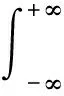
(4)

结构系统振动安全的概率为：

(5)

1.3 单自由度多频激励系统

系统第j个激励和系统固有频率发生不可接受的振动响应的概率为：

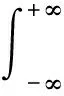
(6)

振动安全的概率为：

Rj=1-Pj

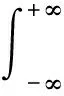
(7)

结构系统振动安全的概率为：

(8)

1.4 多自由度多频激励系统

系统第j个激励和第i阶固有频率发生不可接受的振动响应的概率为：

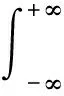
(9)

振动安全的概率为：

Rij=1-Pij

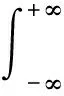
(10)

结构系统振动安全的概率为：

(11)

一般地，无人直升机结构是一个多自由度振动系统，其中的主旋翼和尾旋翼系统是其主要振源。因此，通过公式就可以得到该无人直升机系统的振动可靠度。

2 无人直升机结构系统振动可靠性分析

以某型无人直升机系统为例，通过全机振动模态试验，获得该型无人直升机系统的前7阶固有频率(表1)。影响该型该无人直升机振动水平的一共有两个激振源，分别是主旋翼系统和尾旋翼系统。其中主旋翼转速为471 rpm，尾旋翼转速为3096 rpm。

表1 某型无人直升机模态测试试验结果

文献[6,7]中均将振动系统的激振频率和固有频率假设为正态分布，本例中也假设该型无人直升机系统的两个激振频率和前7阶固有频率均服从正态分布，变异系数分别取0.025和0.05。

根据公式计算得到该型无人直升机系统各阶固有频率和两个激振频率间的振动可靠度(表2)。

表2 各阶固有频率和两个激振频率之间的振动可靠度

根据公式，得到该型无人直升机的振动安全可靠度是0.994444。依照确定性振动分析，两个激振源频率均在各阶固有频率的[0.9,1.1]区间之外，该型无人直升机应该是振动安全的；但是，依据实际飞行及试验情况分析，这种情况下，该无人直升机只能说振动安全的概率比较高，并不是绝对安全。因此，考虑影响固有频率和激振频率参数随机性情况下的振动可靠性分析更贴合工程实际，该方法在无人直升机结构振动设计方面具有一定的应用意义。

3 结论

本文在无人直升机稳定性的振动设计基础上，将无人直升机系统固有频率及激振频率当作服从一定分布的随机变量，提出了振动可靠性分析方法并推导了振动安全可靠度计算公式。最后以某型无人直升机为例，验证了所提振动可靠性方法的正确性。所提振动可靠性设计更符合无人直升机系统结构振动的特点，具有广泛的应用范围。

[1] 飞机设计手册编委会. 飞机设计手册——直升机设计[M]. 北京：航空工业出版社, 2005

[2] 航空航天工业部科学技术研究院. 直升机动力学手册[M]. 北京：航空工业出版社, 1991

[3] 王延荣, 田爱梅. 结构振动可靠性设计方法研究[J]. 航空动力学报, 2003,18(2):191-194

[4] 何晓聪. 单自由度系统振动可靠性计算方法初探[J]. 昆明理工大学学报, 1998,23(2):51-53

[5] 史进渊，杨宇，等.机械零件振动的可靠性设计[J]. 振动工程学报,1999,12(4):553-558

[6] 吕震宙，冯元生. 工程结构振动可靠性分析方法初探[J]. 机械强度,1993,15(6):1-6

[7] 史进渊. 旋转机械零件避开共振可靠度的计算方法[[J]. 机械设计与制造,1995 (4)