数学形态学在Criminisi图像修复算法中的应用

李 尊，吴 谨，刘 劲



数学形态学在Criminisi图像修复算法中的应用

李 尊，吴 谨，刘 劲

（武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

Criminisi图像修复算法的修复步骤由待修复区域的标记、优先权的计算、最佳匹配块搜索与填充和更新置信度4部分组成。其中待修复区域的标记是进行Criminisi图像修复算法的基础，因此合理的标记待修复区域是提高Criminisi图像修复算法修复效果的有效路径。引入数学形态学对待修复图像进行处理，即利用腐蚀与膨胀组合，对待修复区域边缘进行处理，进而进行Criminisi图像修复算法操作。实验结果表明经数学形态学处理后的标记可以降低错误信息的累积，大大提升了图像修复的质量，具有较高的实用价值。

数学形态学；Criminisi算法；图像预处理

0 引言

图像修复[1]是指对受到损害导致信息不完整的图像进行重建或者去除图像中多余的目标。其实质是用待修复图像中存在的信息来恢复缺失的信息，使图像修复整体效果满足人的视觉需求。

针对大区域信息缺失的图像，通常采用基于图像分解的修复技术[2]和基于块的纹理合成技术[3]，其中Criminisi图像修复算法[4]是基于块的纹理合成技术的代表。Criminisi图像修复算法是由Criminisi等人于2004年提出的，其过程是修复区域标记、优先权计算、最佳匹配块搜索与填充、更新置信度。

近10年来，Criminisi图像修复算法的改进主要是针对优先权和最佳匹配块搜索。文献[5]将优先权改进为加权形式，并引入增加平均值补偿和惩罚项，减轻图像修复效果人为痕迹的问题；文献[6]引入曲率到优先权，并将算式改成各项加权和，使得匹配模块更加准确且增强了图像结构的连续性；文献[7]根据修复区域边缘的复杂性，动态的选择搜索区域，降低了时间成本，且一定程度上改善了修复质量。

针对Criminisi图像修复算法第一步即修复区域标记进行研究，优先权计算和最佳匹配块搜索与填充是在修复区域标记基础上进行的，因此第一步做好，是后续工作的基础。

本文将数学形态学[8-9]应用到待修复区域预先标记处理中，并在不同的改进的Criminisi图像修复算法中进行实验。对比实验效果，可以得出通过数学形态学对待修复区域边缘增强，图像的效果有较大的提升。

1 Criminisi图像修复算法

1.1 待修复区域的标记

待修复区域的标记是用与待修复区域形状相似的，面积尽可能小的，颜色特定的图形标记出来。本文是将数学形态学应用到预先标记的待修复图像中。

1.2 优先权的计算

假设待修复图像如图1所示。

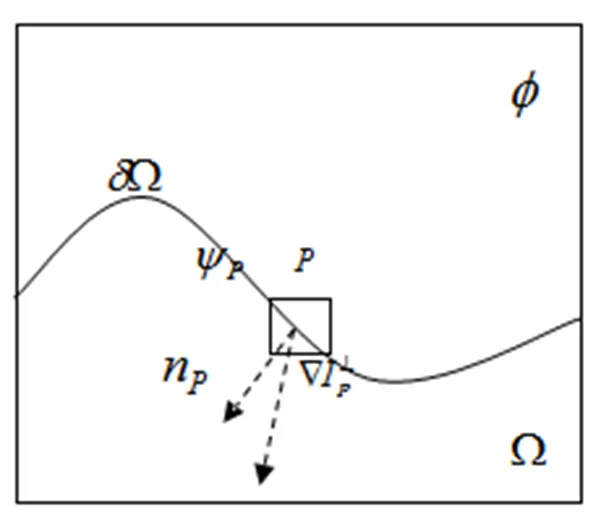
图1 符号说明图

图1中：表示的区域是完好区域，即未标记的区域；表示的区域是破损区域，即标记的区域；表示待修复区域的边界。

Criminisi算法优先权共有置信度()和数据项()两项所决定。其中置信度()表示的是以为中心的待修补块中原图的信息所占的比重；数据项()表示的是边界在处的梯度法向量n与完好区域中边缘梯度向量ÑI⊥的乘积。本文修补块的大小默认3×3。

Criminisi算法提出的点优先权计算如式(1)所示，()、()如式(2)、(3)所示：

priority()＝()×() (1)

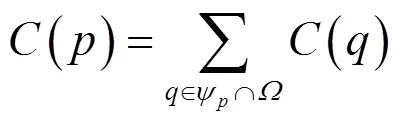
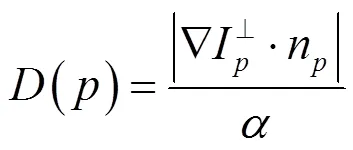
式中：是归一化算子，在灰度图中我们取为255。

置信度()的数值越大优先权越高，表示含有的原图区域的信息多，应给予优先修补；数据项()数值越大优先权越高，表示进化表面线性结构强度高，应给予优先修补。

1.3 最佳匹配块的搜索与填充

通过优先权的计算，确定最大优先权待修补块后，在完好区域进行最佳匹配块的搜索与填充。其匹配原则如下式所示：

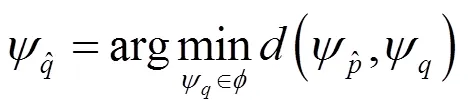
表示待修补块与完好区域中样本块的已知像素的灰度差的平方和最小时，即为最佳匹配块。

1.4 更新置信度

通过最佳匹配块的搜索与填充，使得待修补块变成完好区域中的样本块，置信度也会相应的更新，成为接下来修复工作的依据。

Criminisi算法通过不断重复上述3个步骤，直至待修复区域被填充完毕，则修复完成。

2 数学形态学

数学形态学是法国巴黎矿业学院博士生赛拉和导师马瑟荣于1964年共同提出的，是建立在严格的数学基础理论上并和实际联系广泛的学科。20世纪80年代，数学形态学的发展已趋于成熟，广泛应用于模式识别，图像处理和计算机视觉等方面。

数学形态学以集合概念为基础，膨胀、腐蚀、开启和闭合是其最基本的算子。用4种形态学的基本算子及其组合对图像进行进行形状和结构分析，可用于特征提取、形状识别、边缘检测和图像修复等方面。

本文用到数学形态中最基本的运算形态膨胀与腐蚀[10]，其定义如下式所示：

Å＝{|$∈,∈:＝＋} (5)

Q＝{x|"b∈B,$∈:＝－} (6)

上述式子是应用于二值图像的形态腐蚀与膨胀。其中表示一副图像；表示结构元素，其尺寸要远远地小于且形式是多种多样的，如：圆、菱形、有相线段等。本文选取的结构元素是：圆。

形态腐蚀与膨胀对图像处理有如下效果：

1）形态膨胀：线条变粗，孔隙消失，起到扩展图像的作用。

2）形态腐蚀：线条变细，孔隙扩大，起到收缩图像的作用。

本文在图像预先标记的基础上，采用形态腐蚀与膨胀的基本组合形式，对待修复图像进行处理,即先膨胀后腐蚀。

＝ÅQ(7)

式中：、都为结构元素，形式为圆且满足5≥r≥r≥0。通过数学形态学的处理，待修复区域的边缘得以增强，提高边缘定位的准确性。但尺寸不宜过大，因为过大的尺寸会造成边缘的扩展。

3 实验仿真结果与分析

3.1 待修复的图像预处理

本文针对于图像修复中目标移除情况，在修复区域的预先标记的基础上，利用数学形态学对待修复图像待修复区域边界进行处理，增强Criminisi图像修复算法的修复效果。本文采用的结构元素、均为圆形。处理效果如图2、图3、图4所示。

图2、图3、图4中：(a)是原图；(b)是(a)初始标记图，即未经过数字形态学处理的图像；(c)是经过数字形态学处理后的图像，其中图2中r＝r＝1，图3中r＝1，r＝1，图4中r＝3，r＝0。

初始标记图(b)与数字形态学处理的图(c)进行对比，仅凭人的肉眼相差不大，但在后续的Criminisi图像修复算法中，有举足轻重的作用。

3.2 基于数学形态学的Criminisi算法对比实验

本文实验仿真平台是MATLAB7.0和VC＋＋6.0，仿真结果如图5～图10所示。

图2 蝴蝶的预处理图像

图3 垃圾桶的预处理图像

图4 人物的预处理图像

图5 图2中(b)基础上修复后图像

图6 图2中(c)基础上修复后图像

图7 图3中(b)基础上修复后图像

图8 图3中(c)基础上修复后图像

图9图4中(b)基础上修复后图像

图10图4中(c)基础上修复后图像

实验1目的是移除蝴蝶，处理难点是蝴蝶与花相交处结构和纹理信息的复杂。

实验2目的是移除垃圾桶，处理难点是垃圾桶后背景信息的复杂。

实验3目的是移除背景人群，处理难点是台阶和墙壁的相交处结构和纹理信息的复杂。

图5、图7、图9是在预先标记基础上进行的图像修复；图6、图8、图10是在数学形态学处理的基础上进行的图像修复。

图5、图6、图7、图8、图9、图10中(a)表示Criminisi算法修复的图像结果，(b)表示文献[5]的修复图像结果，(c)表示文献[6]的修复图像结果，(d)表示文献[7]的修复图像结果。

由实验结果对比得出：

1）通过图5和图6，图7和图8，图9和图10对比得出，数学形态学的引入可以大大的减少错误信息的累积，增强了修复效果，满足人的视觉需求。

2）图5、图6、图7、图8、图9、图10中(a)、(b)、(c)和(b)对比得出，数学形态学的引入对不同侧重点的Criminisi算法都有积极的作用，提高了修复质量，增强了图像的整体性。

通过腐蚀与膨胀灵活组合，修复区域的边缘结构信息得到增强，边缘定位的精确度提高，进而修复顺序的可靠性也加大，提高了修复效果，满足人的视觉需要。

4 结束语

通过实验结果对比可以得出，数学形态学在Criminisi图像修复算法中具有举足轻重的地位，通过数学形态学处理待修复区域的标记能起到了增强修复效果的作用。今后需要研究如何智能的选取合理标记的待修复图像，降低修复图像的时间成本及动态的标记待修复图像。

[1] Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting[C]//,,, 2000: 417-424.

[2] 林云莉, 赵俊红, 朱学峰, 等. 基于图像分解的图像修复技术[J]. 计算机工程, 2010, 36(10): 187-192.

Lin Y L, Zhao J H, Zhu X F, et al. Image Inpainting Technology Based on Image Decomposition[J]., 2010, 36(10): 187-192．

[3] 朱文浩, 魏宝刚. 基于样本的纹理合成[J]. 中国图像图形学报, 2008, 13(11): 2063-2069．

Zhu W H, Wei B G. The Technology of Sampled-based Texture Synthesis[J]. Journal of Image and Graphics, 2008, 13(11): 2063-2069.

[4] Criminisi A, Perez P, Toyama K. Region filling and object removal by exemplar based inpainting[J]., 2004, 13(9): 1200-1212．

[5] 杨筱平, 王书文. 基于优先权改进算法的敦煌壁画的复杂区域修复[J]. 计算机辅助设计与图形学报, 2011, 23(2): 284-289．

Yang X P, Wang S W. Dunhuang Mural lnpainting in Intricate Disrepaired Region Based on Improvement of Priority Algorithm[J]., 2011, 23(2): 284-289.

[6] 常晨, 尹立新, 方宝龙. 一种改进的Criminisi图像修复算法[J]. 计算机应用与软件, 2012, 29(9): 238-267.

Chang C, Yin L X, Fang B L. An Improved Criminisi Algorithm for Image Inpainting[J]., 2012, 29(9): 238-267．

[7] 姚建亮, 彭宏京. 一种改进的基于样图的图像修复法[J]. 电子科技, 2010, 23(1): 100-103.

Yao J L, Peng H J. An Improved exemplar-based method for Image Inpainting[J]., 2010, 23(1): 100-103.

[8] 任获荣. 数学形态学及其应用[D]. 西安: 西安电子科技大学, 2004.

Reng H R. Mathematical morphology and Its application[D]. Xi’an: Xi’an university of electronic science and technology, 2004.

[9] 戴青云, 余英林. 数学形态学在图像处理中的应用进展[J]. 控制理论与应用, 2001, 18(4): 478-482.

Dai Q Y, Yu Y L. The Advances of Mathematical Morphology in Image Processing[J]., 2001, 18(4): 478-482．

[10] 吴集林. 论数字图像的膨胀与腐[J]. 广东广播电视大学学报, 2007, 16(1): 105-107.

Wu J L. Digital Image Dilation and Erosion[J]., 2007, 16(1): 105-107.

The Application of Mathematical Morphology in the Criminisi Algorithm of Image Inpainting

LI Zun，WU Jin，LIU Jin

(438001,)

Criminisi algorithm consists of four steps which are marked area. The priority, the best sample patch and updating the degree of confidence, marked area is the basis of Criminisi algorithm, so it is a effective way to improve the effect of Criminisi algorithm. In order to obtain the reasonable marked area, this paper used mathematical morphology in edge, which is corrosion and inflation, and then used Criminisi algorithm of image inpainting. The experiment shows that the marked by mathematical morphology can reduce the accumulation of error messages and improves the quality of the image restoration greatly which has high practical value.

mathematical morphology，Criminisi algorithm，image pre-processing

TP391.41

A

1001-8891(2015)07-0574-05

2015-03-21；

2015-05-20。

李尊（1988-），女，河南省新乡，硕士研究生，从事图像修复研究工作。E-mail：895310276@qq.com。