基于区间参数寻优的PCNN红外图像自动分割方法

王 力，王 敏



基于区间参数寻优的PCNN红外图像自动分割方法

王 力，王 敏

（中国民航大学航空自动化学院，天津 300300）

脉冲耦合神经网络（Pulse Coupled Neural Network）是基于动物视觉图像形成机制，用一组数学式表达这种机制的仿生学方法。PCNN的数学表达式中有7个关键的参数，而其中的阈值放大系数E决定了PCNN网络中每个像素的分割阈值大小。通过平均阈值算法和Ostu算法分别计算出图像的分割阈值，并基于高斯分布模型用数学方法证明了在最小交叉熵时的最佳分割阈值在这2个阈值构成的区间内，通过在这2个阈值构成的区间内搜索新的阈值作为PCNN的参数E的值，并将此寻优的参数E代入改进的PCNN算法进行图像分割。在计算机上进行仿真实验，与基于经验值的指数衰减算法比较，该文算法分割出的兴趣区域清晰、准确，边缘连接性好，信息全面，算法的效率更高，具有很好的实用性。

脉冲耦合神经网络；平均阈值；区间参数寻优；阈值放大系数

0 引言

现在高集成度的电路板在各种工业自动化设备中广泛应用，而电路板的故障检测也越来越受到重视，基于红外图像技术的电路板故障检测方法是一种无损检测方法，在实际中得到广泛应用，这种方法的关键步骤是从红外图像中分割出兴趣区域。红外图像是基于场景辐射的温差成像，表征的是目标物的温度分布，没有立体感、分辨率低、目标边缘模糊平滑、纹理信息少[1]，这使得一些常见的基于梯度的算法分割红外图像的效果不理想。目前国内外已经研究出一些新的红外图像分割算法，BHANU和HOLBEN提出了基于建模的前视红外图像分割算法，较有效的解决了红外图像目标边界模糊的问题[2]。国内也有使用Ostu结合适应模糊阈值的分割方法[3]。

PCNN良好的图像分割性能来源于其数学表达式的迭代，而PCNN数学表达式中的7个主要参数决定了PCNN模型的图像分割性能。Kuntimad研究了模糊目标下参数的设计方法[4]，Bi等采用邻域灰度特性自适应更新算法调节[5]，周东国等采用最小标准差代替参数[6]，邓召学等用GA-BP方法来寻优BP神经网络的阈值[7]，马义德等提出基于交叉熵[8]或最大信息熵[9]的PCNN算法，齐春亮等提出用遗传算法优化PCNN网络阈值震荡系数E[10]，效果较好，但耗时长，算法效率低，鲁棒性差。PCNN图像分割效果还依赖于迭代次数，偏大或偏小的迭代次数都不能达到最好的分割效果，还有基于累积剩余熵[11]、信息测度[12]等方法来得到最佳的迭代次数，但这些算法计算量大，抗噪性能差。PCNN分割图像的关键是阈值震荡系数E的确定，因为PCNN分割图像依赖于每个像素对应的阈值，大于阈值时该像素才点火产生脉冲，图像的点火脉冲图直接决定图像分割的效果。文献[10]采用遗传算法来优化E，用结合最小交叉熵和指数衰减的方法来搜索最佳迭代次数，此方法能得到较好的结果，但计算量很大，耗时长，而且要设定初始阈值。文献[9]使用图像的点火区域的像素均值E，由图像的最小标准差来搜寻最佳迭代次数，此方法需要设定参数E，而最小标准差的数学含义是图像像素信息的离散度，它对应的最小值并不一定表示迭代次数是最佳的，分割效果是最好的。对于文献[9]和文献[10]方法存在的不足，本文提出了在较小区间内进行线性搜索最佳阈值震荡系数E，结合线性迭代和最小交叉熵的方法来得到最佳迭代次数。首先用平均阈值法和Ostu方法分别计算出2个阈值，并用数学方法证明最优值E在这两个阈值构成的区间内，然后在这两个阈值构成的区间内进行线性搜索，得到最佳阈值E和最佳迭代次数，然后将参数E代入PCNN神经网络，经过迭代后就可以得到最佳的分割图像。本文还对PCNN的机理作了详尽的论述。

1 阈值区间的构成

1.1 平均阈值方法

平均阈值法搜索图像的分割阈值是求出背景区域灰度均值和目标区域灰度均值的和，得到这个和的平均值作为下一次迭代的阈值，直到得到一个最终的阈值。其数学表达式为：

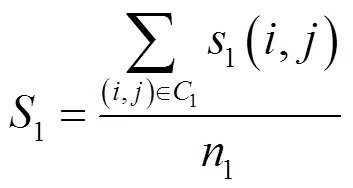
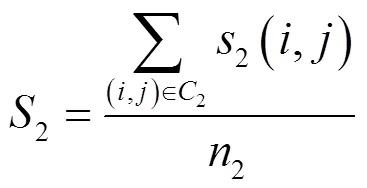
T＝(1＋2)/2 (3)

1＝(m1＋m2)/2 (4)

当|T－T－1|＞时，T＝T－1；当|T－T－1|＜时，终止迭代，得到平均阈值T。

式中：1为背景像素灰度均值；2为目标像素灰度均值；m1和m2分别为图像灰度统计图中灰度值最多的2种灰度值；1为初始化的阈值，将作为迭代终止条件；是一个极小值，当差值大于时，用T代替T－1作为新的阈值分割图像，直到||T－T－1||≤，输出的T即为最终的分割阈值。这种方法不断用背景与目标的灰度均值进行迭代，最终逼近一个稳定的分割阈值，这个阈值体现了背景灰度区域与目标灰度区域间一定的相关性，体现了图像灰度的集中区域，是一个较好的阈值。

1.2 Ostu方法

Ostu方法也叫最大间类法，主要思想是用目标、背景与图像整体灰度均值的方差，当目标与背景灰度的方差和值最小时得到的分割阈值即为最终的阈值[13]。其数学表达式为：

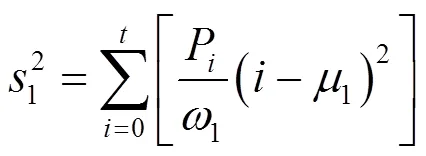
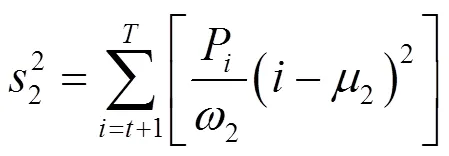
最后的目标公式：

0＝min[11()2＋22()2] (7)

式中：P是灰度值为的像素的概率；1和2分别为目标区域和背景区域的概率；1和2分别是目标和背景的灰度均值，通过迭代，当式(7)值达到最小时，即得到最终的分割阈值0。

1.3 最小交叉熵

对于有限空间内的离散分布的随机变量＝{1,2,3, …,x}，满足(x)＝()，(x)＝()，其概率分布和，有一种度量和相近程度的方法叫Kullback-Leibler距离，又叫交叉熵。K-L散度可用下式表示[14]：

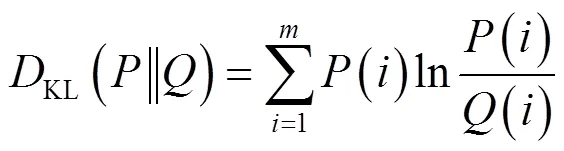
根据熵的定义可知K-L距离实际上是一种差值熵，K-L距离越大，则2个概率分布的差别越大；反之，则越小。交叉熵是用概率论和数理统计的方法研究图像的分割问题，它可以解决多峰函数的最优化问题，交叉熵描述了2个离散量的近似程度，在图像灰度分析中表示2幅图像灰度统计上的近似度，假设图像的分割阈值为，则以此阈值分割的图像的交叉熵的数学表达式为：

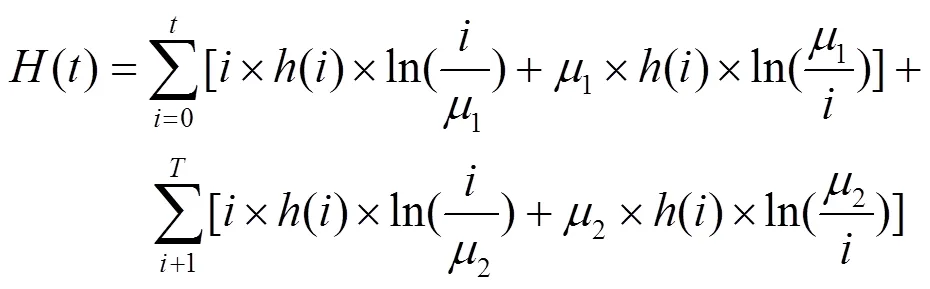
式(9)可以进一步写为如下形式：

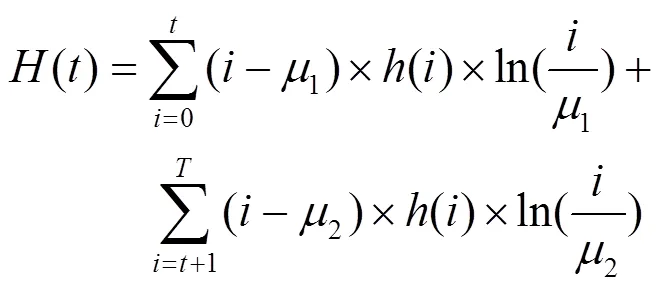
式中：1是背景区域的灰度均值；2是目标区域灰度的均值。这种近似方法类似于数学不规则曲线的积分求和近似，只不过图像分割是在2个区间上近似，而积分是在划分为无限个小区间下近似，交叉熵就相当于积分面积求和时的面积误差，因而最小交叉熵也能体现分割的最佳近似度。因为图像的灰度统计信息是确定的，利用最小交叉熵，通过本文方法迭代，可以找到图像分割的最佳迭代次数和最佳分割阈值。

1.4 阈值区间内的最优VE

本文算法是在平均阈值0和Ostu阈值1之间以最小交叉熵作为寻优E的判断条件进行线性搜索得到最佳分割阈值的，但这样做的前提是证明取得最小交叉熵时的阈值的确是在上述2个阈值构成的区间内，这样才能在上述区间内搜索到最佳分割阈值。下面将通过数学推导证明取得最小交叉熵时的最佳分割阈值的确在此区间内，我们假设最佳分割阈值为，由于电路板图像的目标和背景的灰度比较集中于几个值，比较符合高斯分布的特点，可用极大相似性原理证明，因此我们将图像的目标区域和背景区域的灰度分布都近似为高斯分布，数学式为：

高斯分布式：

为便于进行理论分析，我们用连续高斯分布积分代替原来的离散值求和来得到最小交叉熵，因为目标部分的推理与背景部分一样，其积分形式的最小交叉熵数学式为：

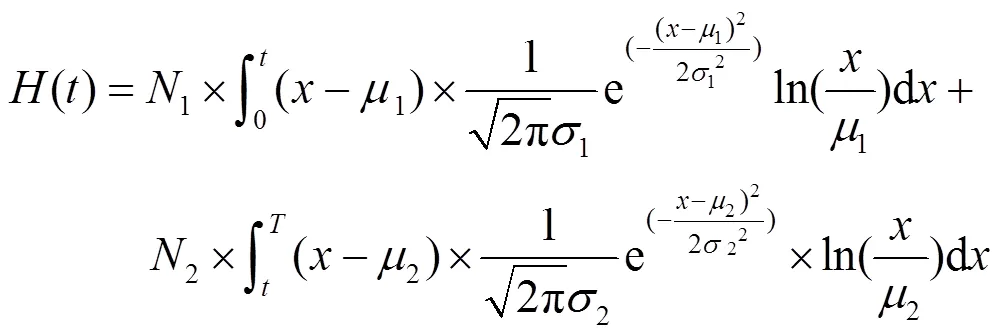
式中：1、2、1、2分别为背景和目标区域的灰度均值和方差值；1、2是背景和目标区域的像素数量，可将式(11)变为：

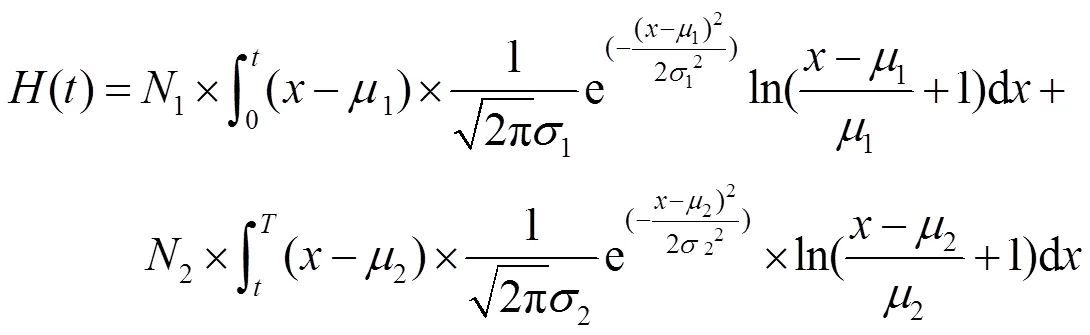
由于图像的背景灰度和目标区域灰度均集中于各自的均值附近，因此对于背景和目标均有(－1)/1＜1，因此可以将式(13)的对数项泰勒展开后略去高阶项，得到式：

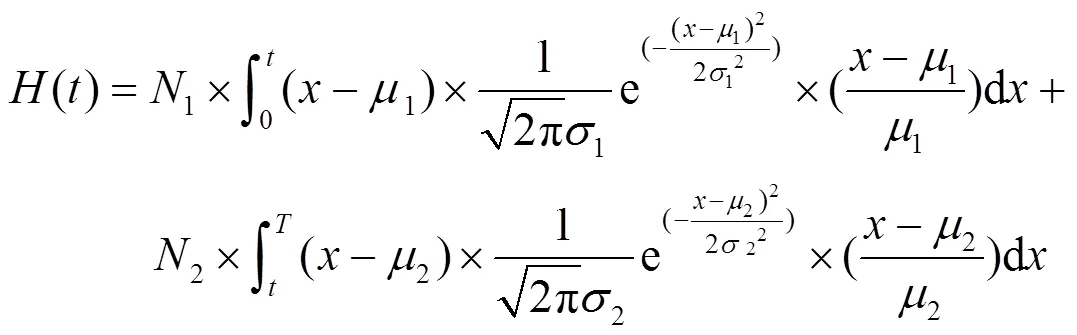
可令－＝，则式(13)变为：

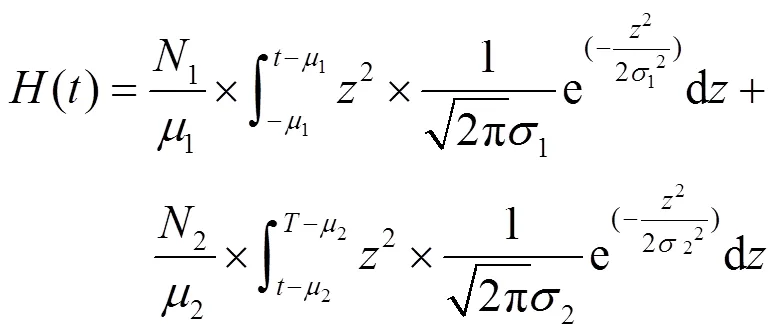
由于上式(15)的两部分结构相同，因此我们只算前一部分的积分，后面部分的结果与前一部分相同，只需参数替换即可得到式(15)的积分，由于我们已经知道本文研究图像的灰度统计信息且知道平均阈值0，以0为阈值初始化分割图像，可以算出背景和目标区域的灰度均值、标准差值，分别为：1＝40.5，2＝181.3，1＝10.8，2＝10.5，1＝28579，2＝36957；由0＝(1＋2)/2，将这6个值代入式(14)可得：

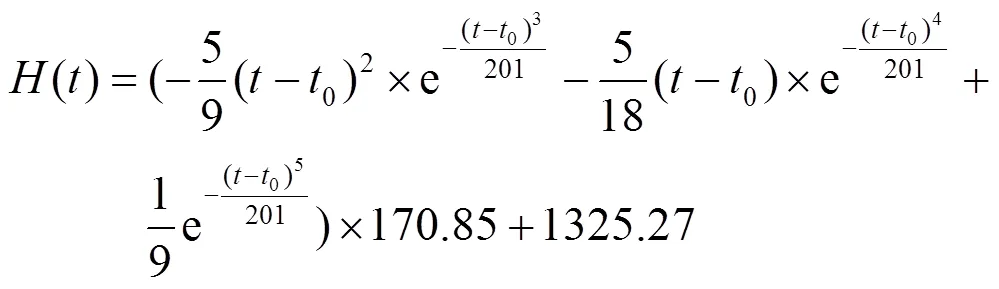
我们可以得到式(16)的曲线图，并对其数学性质进行分析。式(16)的曲线是表示连续高斯分布的图像灰度统计交叉熵与图像灰度集中度的关系曲线，横坐标是图像灰度与平均阈值法得到的阈值灰度的差值，由此曲线可以分析交叉熵与图像灰度分布的数学关系，如下图1所示。

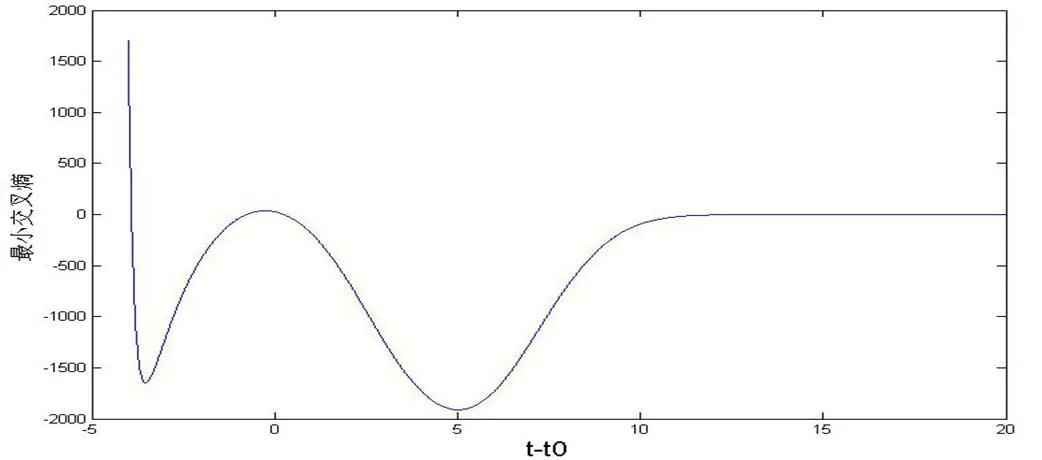
图1 式(16)函数曲线

由图1可以看出在－0＝5和－0＝－4.7处取得最小交叉熵，我们知道高斯分布在|－|＜范围内的概率是0.6824，即图像的大部分像素集中在此区域内，而前面计算出的平均阈值0可以作为灰度均值，平均阈值0和Ostu阈值1的差值可作为标准差值，取得最小交叉熵时的分割阈值在|－0|＜|1－0|内，由此我们证明了区间线性搜索理论上的正确性，即对于灰度较为集中的近似为高斯分布的红外电路板图像，其最佳分割阈值在平均阈值和Ostu阈值区间范围内。

2 脉冲耦合神经网络（PCNN）

2.1 PCNN模型及其参数

PCNN是在动物视觉信息形成原理的基础上建立的仿生学链接模型，是由大量动态脉冲耦合神经元互相连接构成的反馈型神经网络，如图2所示，处理图像时具有良好的尺度不变性、旋转不变性、抗噪性。

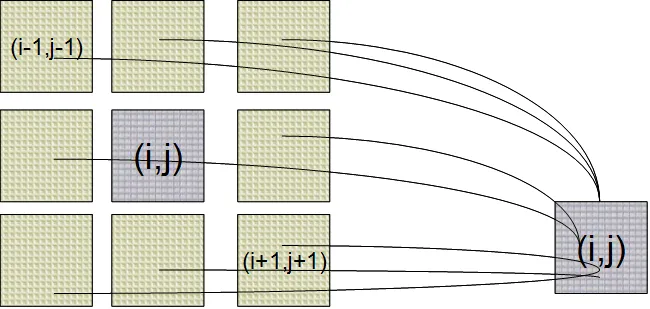
图2 PCNN简单模型

中心像素周边的掩膜内的神经元通过输入权矩阵和耦合连接权矩阵作用于中心的神经元，邻域神经元通过这种耦合链接作用影响中心神经元的脉冲频率，邻域内与中心像素的灰度接近的神经元能与中心神经元同步发放脉冲，PCNN的这种特性使其具有对图像目标区域的边缘检测和分割功能，PCNN的数学表达形式为：

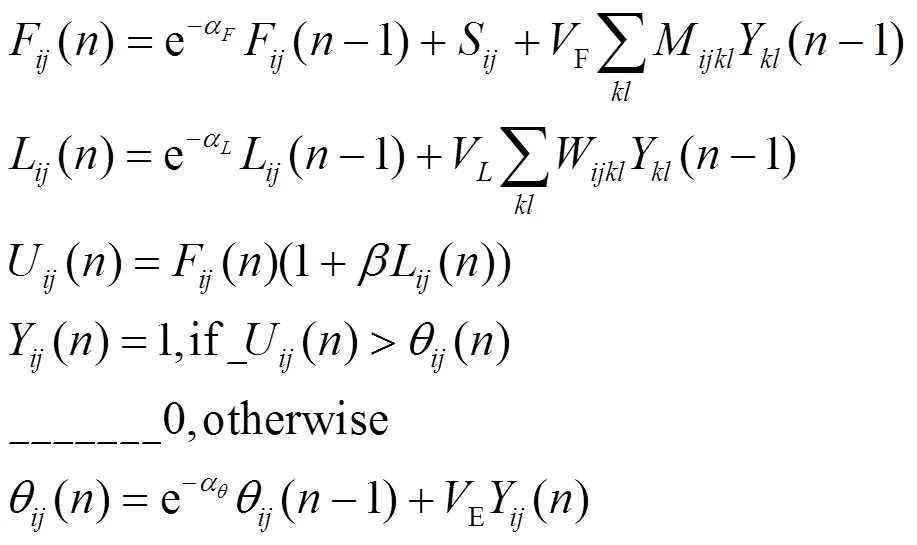
式中：i, j为中心神经元的下标；l, k为周围掩膜内的神经元下标；VF、VL、VE分别为反馈输入放大系数、连接输入放大系数和阈值震荡系数；aF、aL、aq是3个量的衰减系数；b是连接系数；Yij是PCNN的二值输出。不同灰度值像素的点火脉冲图如图3和图4所示。

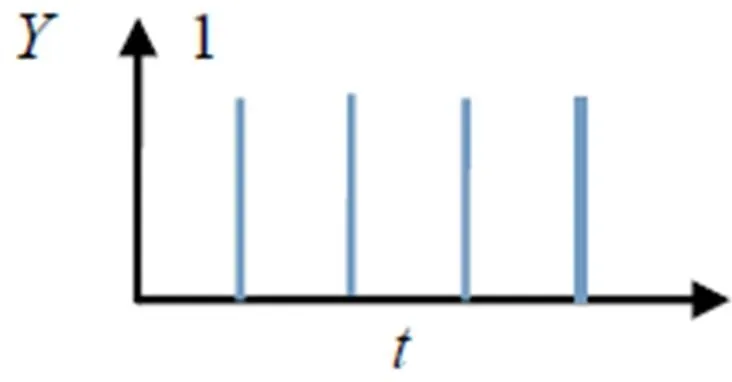
图4 灰度值较小的像素点火脉冲图

2.2 改进的PCNN模型

我们知道PCNN模型是基于动物视觉形成机制产生的仿生学方法，Ranganath等改进Eckhorn[15]的神经元模型后形成的最初的数学表达式也基本反应了动物视觉信息的变化，其中的耦合输出F()和连接值L中的指数衰减漏电积分器是眼睛视觉转移时视神经细胞细胞膜膜电位衰减的数学表示[16]，但在处理红外图像时，输入图像是固定不变的，图像灰度没有空间位置和时间分布上的变化，所以此两项可以去掉，这样更符合红外图像处理的特点，也将PCNN的仿生学视觉模拟形式与实际的红外图像处理相结合，而且作为动物眼睛生理值的F和L也要被图像的中心像素的周围掩膜内的像素替代以体现像素的空间联系，通过对PCNN原始模型的简化，可以减少计算量，减少人为设定参数对图像分割的干扰，同时简化模型保留了同步脉冲发放特性。应用于图像分割的PCNN数学形式为：

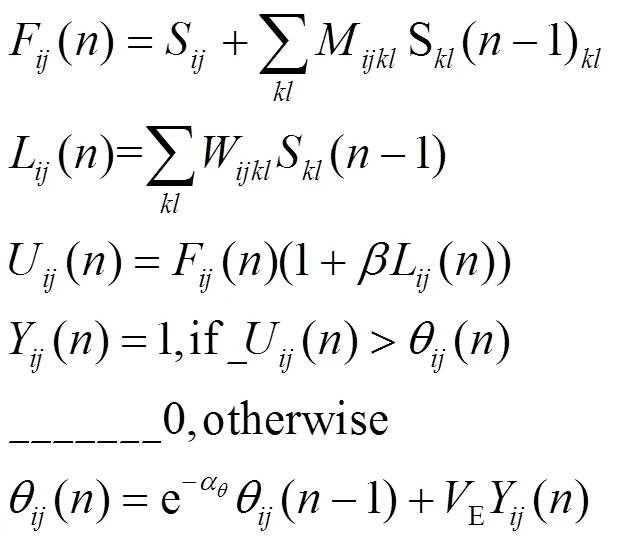
2.3 区间内线性搜索震荡系数VE的方法

一般情况下E的值是一个经验值，目前尚没有一种较好的方法来确定这一参数，本文在前面已经由平均阈值算法得到阈值0和Ostu算法得到的阈值1，我们也通过文献[8]基于指数衰减的最小交叉熵迭代得到最佳迭代次数和另外一个最佳分割阈值2。前面已论证了最优E在平均阈值0和Ostu阈值之间，所以基于这种关系本文用一种新的在区间内线性搜索的算法得到最佳分割阈值和最佳迭代次数；

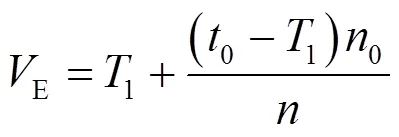
式中：0为迭代的次数；为迭代的总的次数，通过在交叉熵最小时得到一个最佳阈值和最佳迭代次数。本文将上述方法得到的E代入改进的PCNN网络，初始化参数值＝0.1，＝0.3，＝0.5，选择3×3的矩阵结构进行计算，输入权重矩阵的值都为－0.03，连接矩阵权重系数为欧氏距离的倒数，将本文算法在Matlab2010b上进行仿真实验。本文仿真用的是一幅电路板发热的红外图像，目的是要分割出电路板上的发热芯片区域。

3 试验结果分析

将本文方法和列出的其他几种方法分别在Matlab上进行仿真实验，将得到的分割图像从分割效果、保留的图像信息、图像细节、算法效率这些方面进行对比分析，这样可以比较出本文算法的优势所在，如图5所示为指数衰减和本文线性搜索算法的交叉熵变化曲线。

由图5可知，阈值衰减方法和本文区间内线性搜索最佳迭代阈值和最佳迭代次数最终得到的最小交叉熵值很接近，本文算法得到的最小交叉熵值12.92，阈值衰减算法最小交叉熵值为13.07，但本文算法在第5次时就得到最小交叉熵，由图1和图5的对比分析可知，实验仿真与上述理论证明出的在－0＝5处取得最小交叉熵的结果是一致的，而阈值衰减算法在第9次才得到，由于本文算法将阈值约束在一个由2个阈值构成的区间内，所有本文算法的交叉熵在一个较小的区间内波动，而阈值衰减算法的衰减步长难以确定，取值较大，则误差大，难以得到最小交叉熵；取值较小，则搜索时间较长，交叉熵值波动范围较大。本文算法的精确度高，速度快。

由表1可以看出，基于平均阈值、Ostu的线性方法、指数衰减方法得到的最佳阈值很接近，但本文方法迭代次数更少，准确度更高。

如图6所示，本文在Ostu算法得到阈值123和平均阈值算法得到阈值106之间进行线性递增搜索最佳分割阈值，其搜索范围小，速度更快，能够很快的搜索得到最佳分割阈值。而指数衰减算法搜索出的最佳分割阈值正好落在区间内，接近于与线性搜索直线的交点，但其搜索区域太大，若迭代次数少，搜索步长变大，则难以找到准确最佳分割阈值，误差变大，将难以搜索到最佳的分割阈值；若其搜索步长减小，则迭代次数会增加，算法效率降低，其搜索的时间将大大增加。基本PCNN中，脉冲门限是按指数规律衰减的，需按时间步长迭代，而步长的划分直接影响处理速度和分割效果[17]。

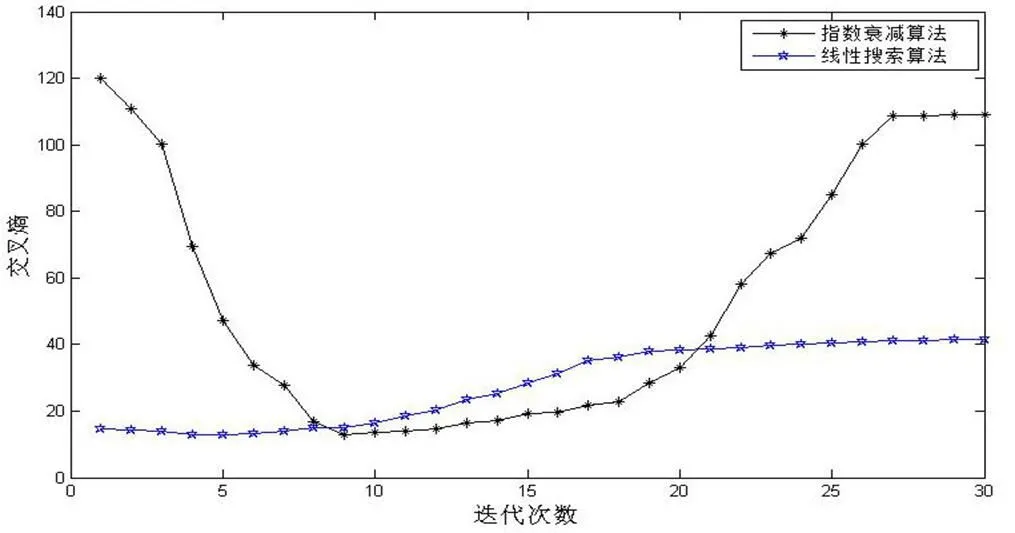
图5 2种算法的交叉熵变化曲线

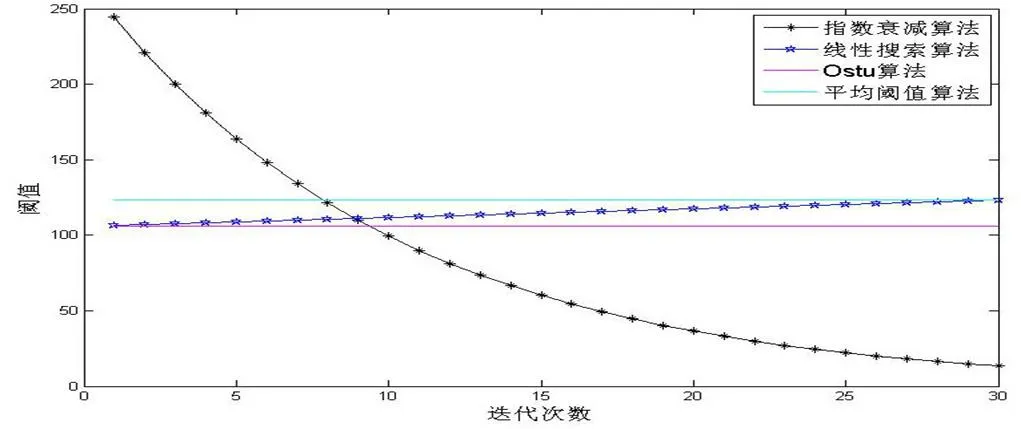
图6 2种算法阈值变化曲线

表1 不同算法的迭代次数和阈值表

由实验仿真得到的对图7的分割图像可以分析：

1）由本文线性搜索方法得到分割图像图11较其他方法图像信息较全面，能分割出电路板中的大多数芯片区域，而且边缘较好，能够分割出其他发热区域。其他几种方法得到的图像信息不完整，不能完全分割出电路板上的主要芯片区域，平均阈值方法和指数衰减方法虽然分割出几块芯片，但边缘粗糙，一些其他较模糊的发热区域也没有分割出来，不能完整的反映芯片信息。

2）观察图8、图9、图10的分割结果知道，图9的分割图介于图8和图10之间，进一步验证了指数衰减的最佳分割值是介于平均阈值方法和Ostu方法之间的一个阈值，仿真实验验证了区间分割方法理论上的正确性。

3）图12是本文方法在设置点火次数为2时的输出二值图，是本文方法在阈值退化到较低时的分割结果，当分割阈值退化到较低时，其分割结果和Ostu方法分割的结果很相近，说明最小交叉熵值和Ostu值之间存在数学上的近似线性关系。

4）由图14和图15分析对比可知，对于可见光图像，本文算法能得到更多的细节信息，分割效果更好，在图像的细微特征处也能显示出较好的轮廓。

5）由图13和图11的对比分析可以观察到本文方法可以从多个目标中分割出某一个特定的目标，并显示出目标的轮廓，这对于电路板红外图像的故障分析尤为重要，对确定故障位置有一定作用，因此本文算法有一定的工程实用价值。

图7 输入的原始电路板红外图像

图9 指数衰减算法分割的图像

图10 Ostu算法分割的图像

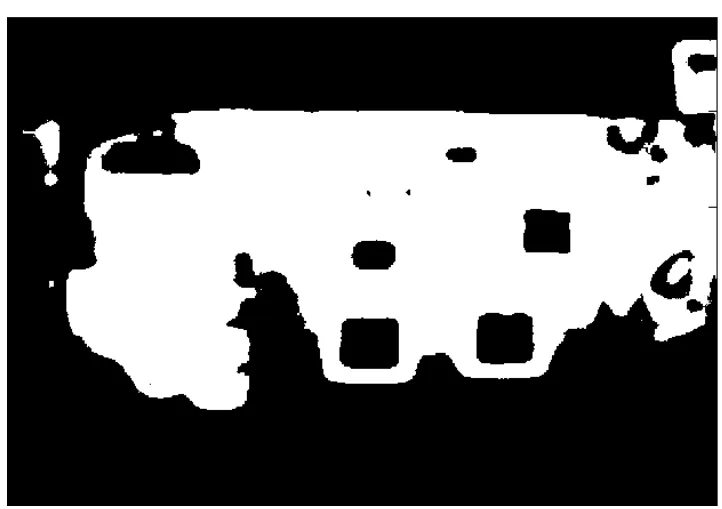
图11 本文线性递增算法分割图像

图12 点火次数为2的分割图像

Fig.12 Segmentation of two ignitions

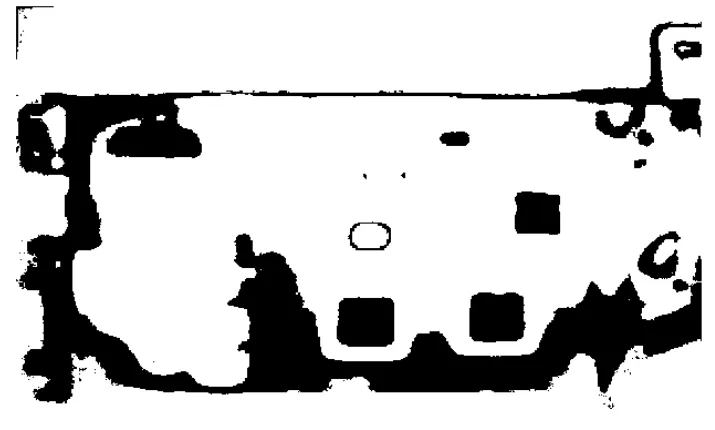
图13 本文目标隔离分割

图14 本文算法分割Lena图

图15 阈值衰减算法分割Lena图

4 结束语

本文结合平均阈值方法和Ostu方法，结合最小交叉熵得到最佳分割阈值，再用脉冲耦合神经网络进行图像分割，结合高斯分布模型从数学角度进行了理论分析，并通过实验仿真进行验证，本文方法对红外电路板图像中一些较模糊的区域也能进行较好的分割，使分割图像的信息得到最大程度的保留，实验结果表明本文方法尤其对背景灰度分布不均的红外图像有较好的分割效果。PCNN在图像处理领域有很好的前景，这种方法比传统的分割方法有多方面的优势，能实现特定目标的分割，能够对电路板红外图像中的故障芯片进行定位，具有一定的实用性。但PCNN方法的数学理论机制目前还没有完全解释清楚，其新的功能还没有完全挖掘出来，这将是未来PCNN方法研究的主要方向，这方面的研究需要进一步加强。

[1] 王力, 曾佩佩, 郝建新. 基于ROI灰度压缩的电路板红外图像配准[J]. 激光与红外, 2014, 44(3): 313-318.

[2] Bhanu, Holben. Model-based segmentation of FLIR images[J]., 1990, 26(1): 2-11.

[3] 王克勇, 蒋一明, 郑链, 等. 坦克目标红外目标图像分割算法研究[J]. 红外与激光工程, 2012, 36(2): 275-278.

[4] Kuntimad G, Ranganath H S. Perfect image segmentation using pulse coupled neural networks[J]., 1999, 10(3): 591-598.

[5] Bi Y W, Qiu T S, Li X B, et al. Automatic image segmen-tation based on a simplied pulse coupled neural network[J]., 2013, 31(74): 405-410.

[6] 周东国, 郭永彩, 郭永彩. 一种参数自适应的简化PCNN图像分割方法[J]. 自动化学报, 2014, 40(6): 1191-1197.

[7] 刘倞, 马义德, 钱志柏. 一种基于交叉熵的改进型PCNN图像自动分割新方法[J]. 中国图形图像学报, 2013, 10(5): 579-584.

[8] 马义德，戴若兰, 李廉. 一种基于脉冲耦合神经网络和图像熵的自动图像分割方法[J]. 通信学报, 2012, 23(1): 46-51.

[9] 齐春亮. 基于遗传算法的脉冲耦合神经网络的自动系统的研究[J].系统仿真学报, 2006, 18(3): 722-725.

[10] 李超, 陈钱, 钱惟贤. 基于交叉累积剩余熵的多光谱图像配准方法[J]. 红外与激光工程, 2013, 42(7): 1866-1870.

[11] 杨海军, 梁德群. 一种新的基于信息测度和神经网络的边缘检测方法[J]. 电子学报, 2014, 29(1): 51-53.

[12] 徐建军, 高山, 毕笃彦, 等. 一种新的图像分割算法[J]. 西安电子科技大学学报:自然科学版, 2011, 38(1): 8-15.

[13] Kullback, S.Leibler, R.A.. On Information and Sufficiency[J]., 1951, 22(1): 23-25.

[14] 刘勍. 基于脉冲耦合神经网络的图像处理问题的研究[D]. 西安: 西安电子科技大学, 2011.

[15] H. S. Ranganath, G. Kuntimad. Iterrative segmentation using pulse neural networks[C]//, 1996, 2760: 543-554.

[16] 张敬贤. 微光与红外成像技术[M]. 北京: 北京理工大学出版社, 1995: 128-130.

[17] 朱冰, 祝小平, 余瑞星. 基于最大熵和PCNN的图像分割新方法[J].红外技术, 2008, 30(5): 259-262.

Automatic Image Segmentation Algorithm by PCNN Based on Mean Threshold and Ostu

WANG Li，WANG Min

(,,300300,)

The Pulse Coupled Neural Network is based on the research of animals’ visual image formation system, which bionics method is presented by a group of mathematics formulas. The formula group of PCNN has 7 key parameters, among which the factor of threshold amplificationEdecides the threshold of segmentation of the image and the output of bilinear image. This article calculates the threshold by the mean threshold and Ostu method, then proves that at the minimum cross-entropy， the best threshold is in the interval of the two thresholds by Gauss distribution model, finally searches a new threshold as the value of PCNN parameterEbetween these two thresholds. We divided the image by using the changed PCNN, simulate the algorithm on the computer and compare the result with experiential decay method. The result shows that our algorithm divides a clear and accurate interesting area, the connectivity is better, the efficiency is better, so this algorithm has a good practicability.

PCNN，Mean threshold，interval parameters optimization，factor of threshold amplification

TP274.52

A

1001-8891(2015)07-0553-07

2015-03-23；

2015-05-20.

王力（1973-），男，重庆人，副教授，博士，主要从事飞行控制、红外图像和模式识别方面的研究。

国家自然科学基金委员会与中国民用航空局联合资助项目，编号：U1333111；APU外部件自动测试平台项目，编号：3122013D021。