基于不变因子的SIFT误匹配点剔除及图像检索

阮小丽，陈庆虎，邱益鸣，鄢煜尘



基于不变因子的SIFT误匹配点剔除及图像检索

阮小丽，陈庆虎，邱益鸣，鄢煜尘

（武汉大学电子信息学院，湖北 武汉 430072）

为解决尺度不变特征变换（SIFT）算法在图像发生旋转和尺度变化时产生的错误匹配问题，提出一种新的算法。根据SIFT提取的关键点信息，利用正确匹配点对间的旋转不变因子和尺度不变因子来剔除SIFT误匹配点，然后对保留下来的特征点进行聚类分析，对目标图像进行识别判断，并通过实验将该算法与双向匹配算法和随机抽样一致性算法（RANSAC）进行比较。实验结果表明，该算法能够有效地剔除误匹配点，且误剔除率低。剔除误匹配点后再进行图像检索，图像的漏检率和误检率都大大地降低了。

尺度不变特征变换；转不变因子；尺度不变因子；误剔除率；漏检率；误检率

0 引言

图像匹配是指在两幅或多幅图像之间根据某一匹配算法找出对应的相似点。实质就是在特征基元相似的前提下，用匹配准则进行最佳搜索。图像匹配在医疗影像和图像检索领域[1]应用广泛，图像匹配正确率直接影响着识别的结果，匹配正确率越高，识别结果越准确。

图像匹配主要可以分为灰度匹配和特征匹配算法[2]。灰度匹配算法按照某种相似性度量方法把每个像素的灰度矩阵与模板图像的所有可能的窗口灰度列阵进行搜索比较来实现图像匹配[3]。图像的特征匹配算法可以克服图像灰度匹配算法对图像仿射变换、尺度变换等比较敏感以及实际应用性差的缺点，并且对图像亮度变化、图像形变和部分遮挡等都有一定的适应性。特征点的匹配算法与位置关系紧密，使匹配的精确度大大提高了。SIFT特征[4]与图像旋转、尺度缩放等无关，在发生光照变化、视角变化、仿射变换以及出现噪声时也比较稳定。SIFT特征独特并且所含信息丰富，即使在海量数据库中也能准确地识别物体。但SIFT算法也有缺点，由于图像的旋转和尺度缩放等变形使得图像间存在错误匹配，导致识别率低，因此进行误匹配点剔除很有必要。

RANSAC算法[5]具有鲁棒性，主要通过反复迭代、不断测试来进行误匹配点剔除。文献[6]提出了一种双向匹配算法，但该算法对误匹配点剔除效果不理想。

对于2幅图像的匹配点对，正确匹配点对间的方向角度差和邻域直径比分布比较集中，错误匹配点对间的方向角度差和邻域直径比呈离散分布的趋势。因此，本文利用正确匹配点对间的旋转不变因子和尺度不变因子剔除SIFT误匹配点，实验结果表明，该算法比双向匹配算法和RANSAC算法更能有效地剔除误匹配点。

1 SIFT算法原理简介

David G.Lowe分别在1999年和2004年提出[7]和总结完善[8]了SIFT算子。林强[9]用Harris角点检测算子进行关键点筛选；李明等[10]在特征点定位和生成特征描述向量时用相位一致性进行代替；卢明等[11]利用Harris算法消除使用Hessian矩阵导致的边界效应。SIFT算法可以分解为如下5步：

1）尺度空间极值检测

实现尺度变换的高斯卷积核是唯一变换核[12]且是唯一的线性核[13]分别经Koendetink等人和Lindeberg等人证明。将一幅图像(,)与尺度可变的二维高斯函数(,,)进行卷积得到该图像的尺度空间(,,)：

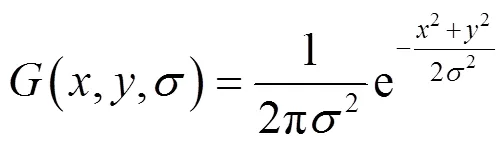
(,,)＝(,,)*(,) (2)

式中：(,)为空间坐标；为尺度空间因子。平滑程度由决定，越大图像被平滑的越多，内容信息越小，越小图像被平滑的越少，细节越丰富。

建立尺度空间后，用高斯差分尺度空间（DOG，scale-space）来检测局部区域的的极值点，DOG算子有如下定义：

(,,)＝[(,,)－(,,)*(,)＝

(,,)－(,,) (3)

选择DOG算子建立DOG尺度空间。

2）检测关键点

在DOG尺度空间中将每个点与其邻近的26个像素中比较后得出的最大值或最小值即为局部极值点。如图1所示，邻近的26个点包括同尺度的8个相邻点以及上下相邻尺度的9×2共18个相邻点。

为了去除DOG算子的边缘响应，需要用Taylor函数对DOG尺度空间检测到的局部极值点进行拟合，然后用Hessian矩阵去掉边缘点，得到稳定的关键点。

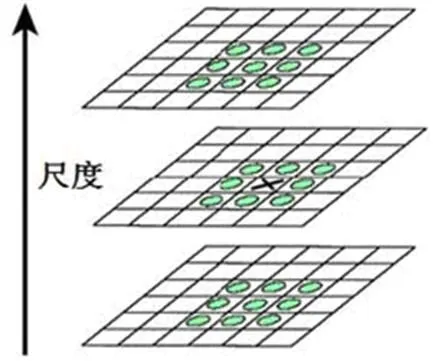
图1 DOG尺度空间关键点检测

3）关键点方向分配

为每个关键点分配1个方向，使SIFT算子具有抗旋转性。关键点方向的获取需要依靠其邻域像素的梯度模值和方向的综合特性：

(,)＝{[(＋1,)－(－1,)]2＋

[(,＋1)－(,－1)]2}1/2(4)

(,)＝tan－1{[(,＋1)－(,－1)]/

[(＋1,)－(－1,)]} (5)

式中：(,)为像素点(,)的梯度模值；(,)为梯度方向。

以关键点为中心，统计关键点邻域采样点的梯度方向直方图。梯度方向直方图将360°分成36个小区间，每个小区间的长度是10°。每一个邻近的采样点相对于中心的关键点梯度方向信息贡献按照高斯函数进行加权，即该采样点的梯度值乘以对应高斯分布函数的值，像素离关键点越近，权值越大。计算出每个采样点的梯度方向，看其属于哪个区间就将其划分到哪个区间。梯度直方图的主峰值即为该关键点的主方向，峰值达到主峰值80%以上的作为辅助方向。

检测完关键点，可以获取关键点的位置、尺度和方向。

4）特征点描述符

首先将坐标轴旋转到与关键点方向一致，使算子与旋转无关。以关键点为邻域窗口的中心取8×8的区域大小，如图2所示。

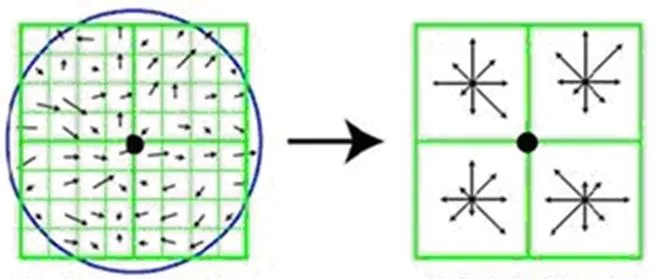
图2 生成特征向量

在图2的左图中关键点即为中央黑点。每个像素在这个区域中用一个小格表示。像素的梯度方向和梯度模值分别由箭头方向和箭头长度指示。图中需要用高斯进行加权的范围为蓝色的圈内区域。每个种子点是在4×4的小区域内计算8个方向的梯度方向直方图并进行累加得到，所以每个种子点拥有8个方向信息。如图2的右图所示，每个关键点又由4个种子点构成。实际应用中，为了增强匹配的稳健性，以每个关键点为中心，取16×16的窗口，扩大采样窗口，得到4×4共16个种子点，每个种子点有8个方向，因此，每个关键点就可以拥有128个数据，即128维的SIFT特征描述子。此时尺度变化、旋转等几何变形因素对SIFT特征向量的影响已经被去除了。为了进一步去除光照变化对SIFT特征向量的影响，可以将特征向量的长度进行归一化。

5）特征点匹配

计算2个特征向量间的欧氏距离[14]，距离越小，说明两者越相似，在测试样本中搜索与训练样本的特征点欧氏距离最小的点和第二小的点，如果最小距离与第二小距离的比值小于某个预先给定的阈值大小，则接受这一对匹配点。阈值越小，匹配点数量越少，但匹配正确率会相应地提高。

2 基于RANSAC算法的SIFT误匹配点剔除

RANSAC算法常用来剔除误匹配点。该算法的思想就是构造一个模型使之符合具体问题的要求，为了得到该模型参数的初始值，需要进行反复提取最小点集，利用这些初始值把原始数据点集分为2类：内点和外点，将所有内点用于重新计算模型的参数。当匹配点集中正确匹配点较多时，该算法能够消除误匹配，但当匹配点集中误匹配点比例较大时，该算法的效果将大大地降低。

3 双向匹配算法

根据交集的思想，有人提出双向匹配算法[5]进行误匹配点剔除。其思想是交换2次匹配中图像的顺序，取2次匹配特征点集的交集部分，即坐标相同的特征点。

4 基于不变因子的SIFT误匹配点剔除

利用SIFT算法检测到的关键点，可以得到关键点的尺度、位置和方向等重要信息。利用SIFT的粗匹配结果可以知道每对匹配关键点的坐标位置、领域直径和方向角度等信息。特征点的邻域直径反映了图像的尺度信息，方向角度反映了图像的旋转角度信息。为了进一步检验他们之间的某种定量关系，选取了10幅训练样本图像和200幅测试样本，其中有目标的15幅，分别为原图，发生旋转和放缩的图像，无目标的185幅。实验过程如下：

1）分别以每幅训练样本为模板，与测试样本库中的图像逐一进行SIFT匹配。

2）根据测试样本有无目标图像以及目标图像进行的变化分为5类：有目标并且图像没有发生变化、有目标图像只进行了尺度缩放、有目标图像只进行了旋转变化、有目标图像同时发生了尺度缩放和旋转变化以及没有目标图像。根据SIFT粗匹配结果，可以得到每对匹配关键点的邻域直径（尺度）大小、方向角度大小，计算每对匹配关键点的邻域直径比值和方向角度差。

3）从2）的计算结果可以发现如下规律：目标图像没有发生变化时，每对正确匹配关键点的领域直径比值等于1，方向角度差为零，错误匹配点的邻域直径比和方向角度差分布离散；目标图像只进行尺度缩放时，每对正确匹配关键点的领域直径比值与图像缩放尺度接近，集中分布在一个小范围内，方向角度差接近零，错误匹配点的领域直径比和方向角度差分布离散；目标图像只进行旋转变化时，每对正确匹配关键点的领域直径比接近1，方向角度差与图像旋转角度接近，集中分布在一个小范围内，错误匹配关键点的邻域直径比和方向角度差分布离散；目标图像同时进行尺度缩放和旋转变化时，每对正确匹配关键点的邻域直径比值与图像缩放尺度接近，集中分布在一个小区域，方向角度差与图像旋转角度接近，也集中分布在一个小区间，而错误匹配关键点的邻域直径比值和方向角度差都呈现离散分布；当测试样本中无目标图像时，每对匹配关键点（错误匹配关键点）的邻域直径比值和方向角度差都是离散分布的。

4）对3）中的统计数据进行归纳总结，可以得出如下结论：当一幅图像进行一定尺度的缩放时，图像正确匹配关键点的邻域直径也会进行相应倍数的缩放；当图像进行任意角度的旋转变化时，图像正确匹配关键点的方向角度也会进行相应角度的旋转变化。

5）利用4）所总结出的规律，可以得出SIFT误匹配点剔除的基本原理。当图像进行旋转和尺度缩放等变化时，每对正确匹配关键点的领域直径比值会发生相应倍数的变化，每对正确匹配关键点的方向角度差也会出现与旋转角度类似的变化，而错误匹配关键点间的邻域直径比和方向角度差呈现离散分布的趋势，并无此规律。计算每对匹配关键点的邻域直径比和方向角度差，对计算结果进行分析，去掉分布离散的数据点就可以剔除误匹配点了。算法的核心步骤如下：

①根据SIFT匹配结果可以获得每对匹配点的邻域直径和方向角度大小。令p、q为任意一对SIFT匹配点（p表示训练样本中的匹配关键点，q表示测试样本中的匹配关键点），通过匹配信息可以知道每对匹配点对应的训练样本和测试样本的特征描述子索引。进而知道每对匹配点在分别在训练样本和测试样本中的关键点索引，从而知道每对匹配点对应的邻域直径和方向角度大小，计算每对匹配关键点的邻域直径比和方向角度差，即q与p的邻域直径比，q与p的方向角度差。由于方向角的取值范围为[0, 360)°，为了防止因图像旋转后超过360°产生溢出，导致方向角度差出现负数的情况，当两者的方向角度差出现负值时在负数的基础上再加上360。

②根据5）可知每对正确匹配关键点的邻域直径比和方向角度差都集中分布在一个小范围内。称正确匹配关键点的邻域直径比的分布区间为尺度不变因子，正确匹配关键点的方向角度差的分布区间为旋转不变因子。

邻域直径比为：

z＝z2/z1(6)

方向角度差：

if (g2＞a1)

g＝g2－g1

elseg＝g2－g1＋360 (7)

式中：z、g分别表示每对匹配关键点的邻域直径比和方向角度差；z2、g2分别表示q的邻域直径大小和方向角度大小；z1、g1分别表示p的邻域直径大小和方向角度大小。

③SIFT错误匹配关键点的邻域直径比与尺度不变因子相差较大，方向角度差与旋转不变因子相差较大。根据这个原理统计每对匹配点的邻域直径比和方向角度差，将邻域直径比和方向角度差作为两类数据，去掉两类数据中离散分布的数据，取两类数据中都保留下来的点作为SIFT误匹配点剔除后的结果。步骤如下：

Step1：将所有的邻域直径比值作为数据源，取其中任意一个数据，统计该数据源中其他数据点到该数据点的欧式距离小于阈值1的点数，欧氏距离公式如式(8)所示：

＝[(1－2)2＋(1－2)2]1/2(8)

统计点数若大于阈值num1，则认为该数据点分布集中，是正确匹配点，应该保留，否则，应该从该数据源中去掉。对该数据源中其他数据点也按此方法进行统计判断，得到一组数据点。将所有的方向角度差作为另一类数据源，按照同样的处理方法，可以获得另一组数据点。

Step2：取两类数据中保留下来的数据点所代表的匹配关键点的交集，作为最后误匹配点剔除后的结果。

5 剔除误匹配点后的图像检索

1）按照步骤(3)对保留下来的匹配点进行进一步聚类分析[15]，去掉那些分布离散的匹配点，得到聚类点。

2）从聚类点中任取一点，计算其他所有点到该点的欧式距离和，取欧氏距离和最小的点作为这些点的聚类中心：

式中：0为所有聚类点到某个聚类点的欧氏距离和；x，y为聚类点的坐标；，为某个特定聚类点的坐标；为总的聚类点数。

3）根据公式(9)计算所有聚类点到聚类中心的欧氏距离和，若欧氏距离和与聚类点数的比值小于阈值，则认为该测试样本中有目标图像，反之则没有。

6 实验结果分析

在SIFT粗匹配的基础上，将本文算法与双向匹配算法和RANSAC算法进行误匹配点剔除和检索的实验结果进行对比来检验文中算法的好坏。算法性能的好坏主要根据匹配正确率、误剔除率、漏检率和误检率进行评估。

6.1 算法性能评价指标

匹配正确率＝正确匹配点数/总匹配点数 (10)

误剔除率＝剔除的正确匹配点数/总剔除点数 (11)

漏检率＝未检索到的目标图像数/总的目标图像数(12)

误检率＝检索到的无目标图像数/总的无目标图像数(13)

6.2 实验结果及分析

实验中采用100组普通训练样本图像，2000幅测试样本图像，其中有100幅测试样本含有目标图像，分别为20幅原目标图像，40幅包含目标图像的大图像，40幅包含经过旋转和尺度缩放的目标图像，其余为无目标图像。本文所采用的程序设计语言为VS2008和开源库OpenCV2.4.5，以灰度图的方式读取两幅图片，对灰度化以后的图片进行SIFT特征匹配、误匹配点剔除及检索等一系列的操作。部分误匹配点剔除实验图如下：

实验一：

图3(a),(b),(c),(d)分别为SIFT粗匹配、双向匹配算法、RANSAC算法和本文算法的实验结果图。其结果如表1所示。

图3 SIFT匹配及3种算法对比图

表1 SIFT匹配及3种算法结果对比

实验二：

图4(a),(b),(c),(d)分别为SIFT粗匹配、双向匹配算法、RANSAC算法和本文算法的实验结果图。其结果如表2所示。

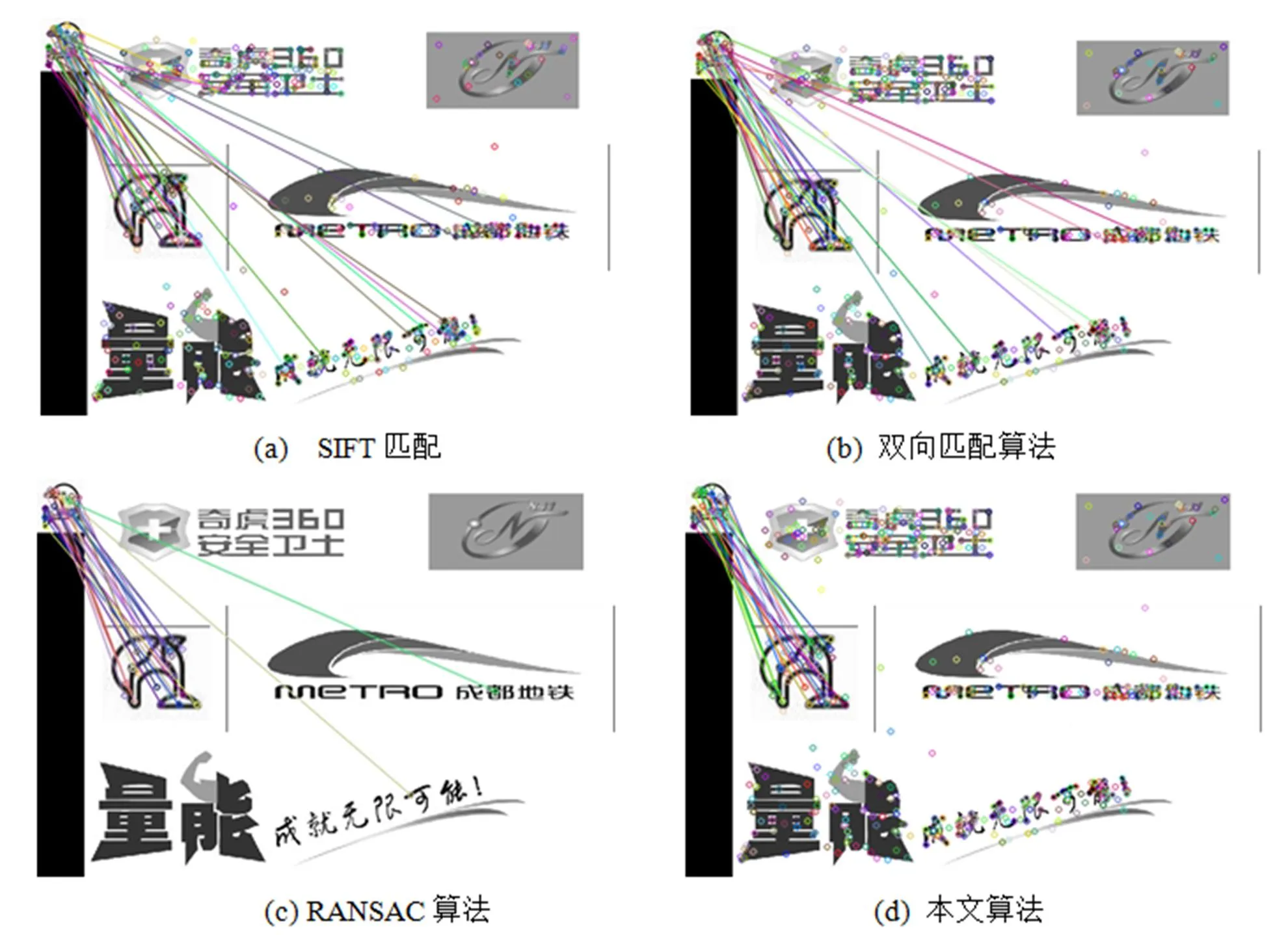
图4 SIFT匹配及三种算法对比图

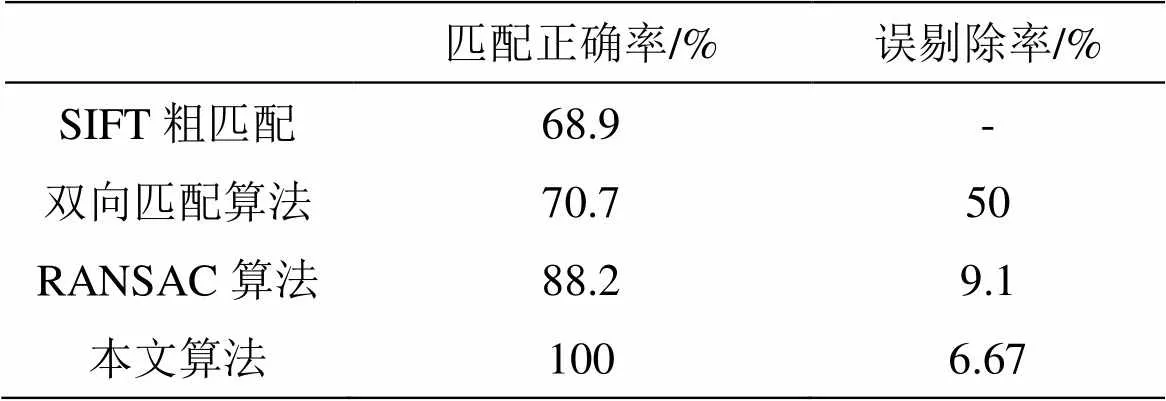
表2 SIFT粗匹配及3种算法结果对比

从表1、2可以看出：①当SIFT粗匹配正确率较低时，双向匹配算法并不能达到有效剔除误匹配点的效果，RANSAC算法能够在一定程度上提高匹配正确率，但提高幅度不大且误剔除率较高，而本文算法在有效剔除误匹配点的同时还可以保证低的误剔除率；②当SIFT粗匹配的正确匹配点多于误匹配点时，双向匹配算法能稍微提高匹配正确率，但误剔除率较高，RANSAC算法虽然能够剔除误匹配点，但性能没有本文算法好。

选取100组训练样本，2000幅测试样本，用上述3种算法分别剔除误匹配点后再检索的实验结果与直接进行检索的实验对比结果如表3所示。

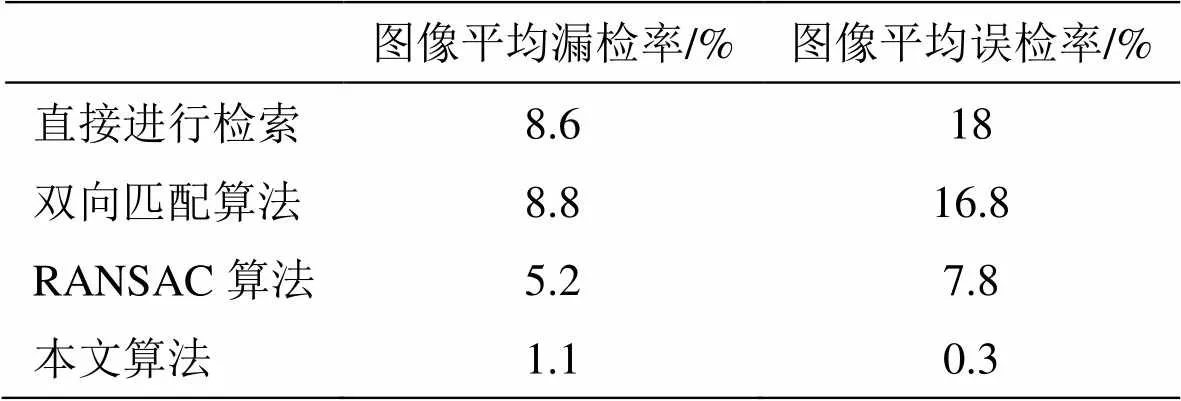
表3 三种算法误匹配点剔除前后图像检索结果对比

由表3可知，用双向匹配算法剔除误匹配点后再进行检索，并不能有效地提高图像检索率，RANSAC算法虽然能够在一定程度上降低平均漏检率和误检率，但不及本文算法效果好。

7 结论

本文针对图像旋转和尺度变化导致的SIFT误匹配，提出基于旋转不变因子和尺度不变因子对其进行误匹配点剔除。经过大量的实验验证，本文算法的优越性明显高于另外两种算法：双向匹配算法并不能有效地剔除误匹配点且对图像检索正确率的提高贡献不大，RANSAC算法虽然能够在一定程度上提高图像的匹配正确率和检索率，但当SIFT粗匹配中误匹配点较多时，效果不太理想，本文算法不论在误匹配点多还是少的情形下，都能够有效地剔除误匹配点，且误剔除率较低，大大地降低了漏检率和误检率。本文算法效果好、原理简单、适用范围广，利用本文算法可以找到图像的旋转角度因子和尺度缩放因子将图像进行还原，将还原后的图像再进行模式识别，可以大大提高识别率。今后可以将本文算法用于互联网海量图像检索。

[1] 周颖. 基于SIFT算法的图像特征匹配[J]. 现代计算机:专业版, 2015(5): 63-68

[2] Kuglin C D，Hines D C．The Phase Correlation Image alignment method[C]//1975: 163-165．

[3] 屠文柯, 阎保定, 杨海涛. 一种基于仿生学原理的复杂彩色目标辨识方法[J]. 河南科技大学学报, 2005, 26(6): 67-69.

[4] 余宏生, 金伟其. 视频图像的SIFT特征点自适应提取算法[J]. 红外技术, 2013, 35(12): 768-772.

[5] M. A. Fischler, R.C.Bolles. Random Sample Consensus：A paradigm for model fitting with applications to image analysis and automated cartography[J]., 1981, 24(6): 381-395

[6] 骞森, 朱剑英. 基于改进的SIFT特征的图像双向匹配算法[J]. 机械科学与技术, 2007(9): 1179-1182.

[7] David G. Lowe. Object recognition from local scale-invariant features[C] //, 1999(9): 1150-1157.

[8] D.G. Lowe. Distinctive image feature from scale-invariant keypoints[J]., 2004, 60(2): 91-110.

[9] 林强. 一种改进的SIFT图像匹配算法[J]. 现代计算机:专业版, 2015(5): 58-62.

[10] 李明, 李德仁, 范登科, 等. 利用PC-SIFT的多源光学卫星影像自动配准方法[J]. 武汉大学学报: 信息版, 2015(1): 64-70.

[11] 卢明, 张晶. 基于Harris的改进SIFT算法[J]. 兰州交通大学学报, 2014(6): 11-15.

[12] Koenderink J.J. The structure of images[J]., 1984 (50): 363-396．

[13] Lindeberg, T. Detecting salient blob-like image structures and their scales with a scale-space primal sketch: a method for focus-of-attention[J]., 1993, 11(3): 283-318.

[14] 李涪帆, 田浩, 巨永锋. 基于欧氏距离的交通警告标志识别方法研究[J]. 微型机与应用, 2014, 22: 47-50.

[15] 杨传慧. 图像聚类及其在图像检索中的应用研究[D]. 南京: 南京师范大学, 2013.

Excluding SIFT Mismatching Points Based on the Invariant Factors and Image Retrieval

RUAN Xiao-li，CHEN Qing-hu，QIU Yi-ming，YAN Yu-chen

(,,430072,)

A new algorithm was put forward to solve SIFT mismatching problem that was caused by the image rotation and scale changes. It used the image rotation-invariant and scale-invariant factors of the right matching points to eliminate the mismatching points with the key information of SIFT extraction. Then it analyzed the reserved feature points by clustering to recognize the target images and was compared with the bidirectional matching algorithm and RANSAC algorithm through the experiments. The experiment results showed that this algorithm can effectively eliminate the false matching points and the false rejection rate is low. Images are retrieved after the mismatching points excluded，and the miss rate and the false detection rate of the images are greatly reduced.

SIFT，rotation-invariant factor，scale-invariant factor，false rejection rate，miss rate，false detection rate

TP391.41

A

1001-8891(2015)07-0560-06

2015-03-24；

2015-05-20.

阮小丽（1990-），女，湖北孝感人，硕士，主要研究方向：图像处理与模式识别。

文件检验鉴定公安部重点实验室（中国刑事警察学院）资助项目，编号：11KFKT002。