基于GT的钟差预测模型辅助GPS定位算法研究

刘伯鸿，靳文军，徐志奇

（兰州交通大学 自动化与电气工程学院，甘肃 兰州730070）

GPS定位系统是一种高精度、快速度的连续定位系统。目前该系统已经在车辆定位、地壳运动监测、变形监测等诸多领域得到了广泛应用［1］。利用GPS系统进行定位时，用户接收机只有接收到至少4颗以上的卫星时才能实现定位解算。而在峡谷或城市楼群环境中信号易受到遮挡而只接收到3颗卫星时，利用传统的定位算法无法实现接收机的定位解算［2］。通常都是利用惯性导航系统、虚拟卫星以及地图匹配等辅助GPS定位，在一定程度上解决了3颗卫星无法定位的问题，但是以上方法需要额外增加 硬 件 设 备，增 加 了 定 位 成 本［3－5］。本 文 利 用GPS接收机在定位时提供的接收机钟差数据辅助GPS定位，该方法只需要在接收机的内部嵌入相应的算法而不需要增加额外的硬件设备。在受到强烈的环境干扰的情况下依然可以实现接收机的定位解算功能。

灰色系统是用来解决信息不完备系统的数学方法［5］，本文将GPS接收机钟差序列的变化过程看做是一个灰色系统，利用灰色理论对卫星钟差进行预测；并在GPS卫星受到干扰的条件下利用预测的钟差值辅助GPS接收机进行定位。

1 灰色理论的钟差预测模型

灰色理论研究的是一种对贫信息的建模，它提供了在贫信息的情况下如何解决系统问题的新途径［6－8］。通常情况下系统的原始数据都不具备规则性，而可以通过利用累加生成的方法去逼近系统，对系统进行累加处理之后，生成有规律的数据，从而降低数据的随机性［9－10］。

对序列Z ＝ ［Z（1），Z（2），…，Z（L）］建立灰色模型的过程如下：

1）首先需要对系统原始的序列Z进行一次累加，生成新的序列Z（1）。

2）对序列Z（1）的指数规律性进行检验。（）

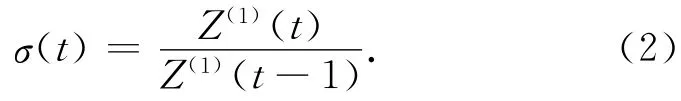
当t＞3时，如果1＜σ（t）＜1．5，则新生成的序列Z（1）具有指数规律，可以对其建立灰色模型。

3）对新生成序列Z（1）建立微分方程

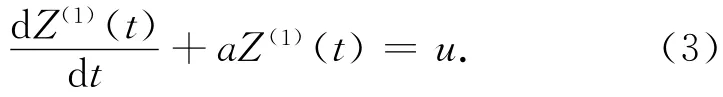
4）将式（3）写成矩阵形式

其中，

5）依据最小二乘法的方法，对a和u参数进行估计

6）通过利用a和u的估计值~a和~u，计算新生成序列Z（1）的预测序列如式（7）所示。

7）对预测序列~Z（1）进行一次累减操作，将得到原始序列Z的预测序列~Z如式（8）所示。

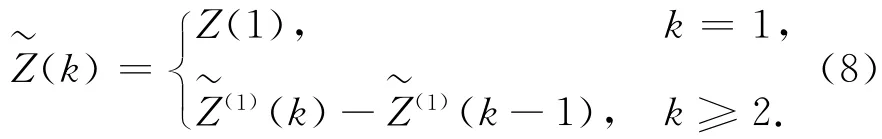
基于灰色理论的接收机钟差预测模型，其对系统原始的钟差序列不需要做出任何的统计规律的假设［3］，故其具有广泛的适应性。

2 钟差预测模型辅助定位

2．1 GPS伪距定位原理

当GPS接收机可以观测到N颗卫星时，则GPS的伪距方程为

式中：ρi为第i颗卫星的伪距测量值；Ri为第i颗卫星到用户接收机的几何距离；b为接收机与卫星的钟差；εi为系统的测量误差。

将式（9）在接收机的概略坐标 （x0，y0，z0）处进行泰勒级数展开，并且忽略掉二阶以上的高次项，得到线性化观测方程

式中：L∈RN×1为伪距差向量；H∈RN×4为系数矩阵；X ∈R4×1包含了 GPS接收概略坐标 （x0，y0，z0）的改正数δx，δy，δz。

式（10）中含有4个未知的参数，所以需要至少4颗卫星数据才能进行解算。当在复杂环境的情况下，由于GPS卫星信号受到遮挡，接收机只能接收3颗有效卫星。此时，系统只能提供3个观测方程，故无法对4个未知数进行解算，以至于GPS接收机无法正常定位。

2．2 钟差辅助GPS接收机的定位解算

为了解决GPS接收机在只有3颗有效卫星的条件下不能定位解算的问题，在观测方程中引入通过灰色理论预测得到的钟差值，通过扩充观测矩阵来实现对GPS接收机的定位解算。

利用钟差预测模型辅助GPS接收机定位解算时，将预测的钟差值B替代实际的钟差值b，则系统方程为

式中：L′∈RN×1为扩展后的伪距差向量；H′∈RN×3为扩展后的系数矩阵；X′∈R3×1包含了GPS接收机概略坐标 （x0，y0，z0）的改正数δx，δy，δz。

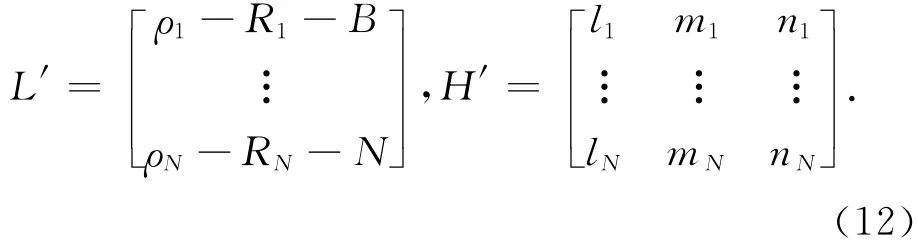
式中：l1，m1，n1为GPS接收机与第i颗卫星之间的方向余弦，其中

式中：（x0，y0，z0）为接收机的坐标；（Xi，Yi，Zi）为第i颗卫星的坐标。

由式（10）和式（11）可以看出，在引入了钟差预测模型以后，定位解算的未知参数变成了3个。所以，利用钟差模型辅助的方法在只有3颗卫星的条件下，可以实现对GPS接收机的定位解算。图1为钟差辅助GPS定位解算的流程。

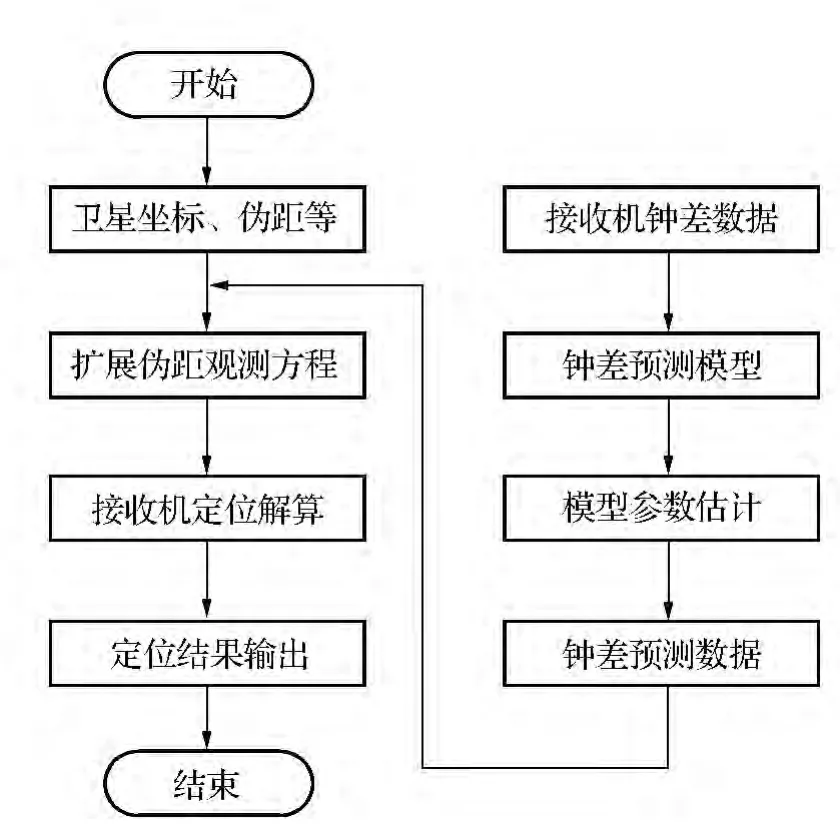
图1 钟差辅助定位解算流程

3 钟差预测模型辅助定位实验验证

本文利用GPS接收机的实际测量所得的卫星坐标、卫星伪距和GPS接收机钟差等相关数据，对钟差预测模型辅助的GPS定位方法在静态情况下进行了验证分析。

3．1 实验条件

GPS接收机持续采集卫星定位数据5 min，每1 s为一个采样间隔，共获得了300组定位数据。提取前4 min所采集到的钟差数据并利用这些数据建立预测钟差模型，然后预测第5 min钟差，利用预测值辅助GPS接收机定位。用于建模的接收机钟差如图2所示。

图2 实验所用钟差数据

由图2可以看出，GPS接收机的钟差数据较大，若直接利用这些数据建立钟差预测模型的话可能会使得最终的运算量过大，不利于定位解算。因此对该序列进行一次差分运算，然后对经过差分运算所得到的新的序列进行灰色预测模型的建立。

3．2 模型预测能力分析

为了确保模型建立的合理性需要在模型建立之前对序列的指数型规律进行一次检验。图3为序列指数规律的评价指标σt

图3 差分序列的指数规律

由图3可以看出，1＜σ（t）＜1．5，差分序列满足指数规律，可以对其进行灰色模型的建立。

由图4可知，钟差预测的平均误差为14．473 m，并且随时间的增大，钟差预测误差的值也随之增大。但是在241～280 s之间其预测误差的值基本保持在一定水平没有太大的波动，所以在较短的预测时间内，模型能够很好地反应出钟差序列的变化趋势。

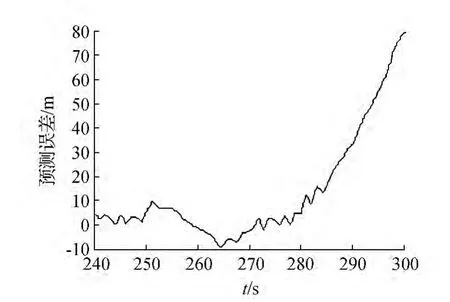
图4 钟差预测误差

灰色理论用指数曲线去拟合原始数据，最终预测结果为一条平滑曲线。序列随时间的增长逐渐偏离指数的固有特征，这样便使得最终的预测误差越来越大。因此，基于灰色理论的接收机钟差预测模型适合于短期预测。

3．3 钟差方式辅助GPS定位解算

利用以上的钟差预测模型辅助GPS接收机实现最终的定位解算，结果如图5所示。

由图5可知，基于钟差预测模型对于GPS辅助定位的精度效果明显。在241～280 s之间进行预测时，其定位的误差最大没有超过30 m，这个定位结果能够满足短时间的定位精度的要求。但是由于存在预测误差的累计，随着时间的持续增长，使得定位误差越来越大；而当预测时间超过60 s时，其定位误差超过了80 m，此时的定位解算得出的结果误差过大，只具有一定的参考价值。

图5 X轴方向的定位误差

4 结束语

本文提出了一种基于灰色理论的钟差预测模型辅助GPS定位的方法实现GPS卫星不完备情况下的接收机的定位解算。验证结果表明该模型可以辅助GPS在其不完备条件下的定位解算。此外通过钟差方式辅助定位结果的精度与钟差预测精度有直接的关系。如何通过提高钟差预测的精度来进一步提升钟差模型辅助定位的精度是下一步需要解决的关键问题。

［1］ 郑睿，陈杰．信号短暂缺失下的非完备GPS定位算法研究［J］．电子科技大学学报，2009，38（4）：496－500．

［2］ WU Y，GUO J M．Single point positioning with sequential least－squares filter and esti mated real－time stochastic model［J］．Geo－Spatial Infor mation Science，2008，11（1）：13－16．

［3］ 丁传炳，王良民，常思江．制导火箭GPS INS全组合导航系统仿真研究［J］．仪器仪表学报，2010，31（5）：1179－1193．

［4］ 何秀凤，陈永齐，桑文刚，等．GPS伪卫星组合定位方法及其在变形监测中的应用［J］．南京航空航天大学学报，2007，39（4）：496－500．

［5］ HOU Y L，LUO D．A decision model based on grey rough sets integration with inco mplete inf or mation［J］．Chinese Quarterly Journal of Mathematics，2009，24（1）：151－158．

［6］ XIA X T，WANG Z Y．Grey relation bet ween nonlinear characteristic and dynamic uncertainty of rolling bearing friction torque［J］．Chinese Journal of Mechanical Engineering，2009，22（2）：244－249．

［7］ YANG Q M，SUN J M．A location method for autonomous vehicle based on integrated GPS／INS［C］．IEEE Inter national Conference on Vehicular Electronics and Safety，Beijing China，December 13－15，2007．

［8］ PHTAK M，CHANSARKAR M，KOHLI S．Positon fix from three GPS satellites and altitude：a direct method［J］．IEEE Transactions on Aerospace and Electronic System，1999，35（1）：350－354．

［9］ 段宇，吴江飞．基于EKF和自适应抗差滤波的星载GPS定轨方法［J］．测绘工程，2014，23（1）：21－24，30．

［10］傅惠民，刘成瑞，马小兵．时间序列均值和方差函数的确定方法［J］．机械强度，2004，26（2）：164－169．

［11］王尔申，张淑芳，胡庆．基于时钟偏差模型的GPS不完整星座定位方法［J］．大连海事大学学报，2009，35（2）：59－62．