基于加测陀螺定向边的井下支导线升级改造

马 强

（绍兴市柯桥区土地测绘大队，浙江 绍兴312000）

由于受井下巷道条件的限制，井下平面控制测量为基于支导线的形式沿巷道布设的导线测量。井下导线边长一般较短，通常为直伸形。一般先以低等级的工作控制导线指示巷道掘进，当巷道掘进300～500 m后，再布设高等级的基本控制导线，用来检查前面已布设的工作控制导线是否正确，如此不断分段施测，直到井巷工程相继施工贯通后才形成闭（附）合导线或导线网。

特别是矿山重大井巷贯通工程测量的内容往往是专用支导线的施测，经贯通测量误差预计后，发现支导线精度满足不了贯通允许偏差时，必须研究井下支导线的升级改造，以达到贯通允许偏差要求。

1 井下支导线升级改造

1．1 井下支导线

按规定，井下支导线（见图1）必须是复测支导线的形式。

如图1所示，当导线复测T次，且每次复测时导线各转折角为等精度观测，则支导线终点k的点位中误差

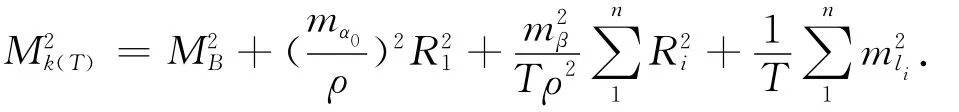
式中：MB为导线起始点B点位中误差；mα0为导线起始边AB坐标方位角中误差；Ri为导线第i点与终点k连线的长度（i＝1，2，…，n）；mli为导线各边（单程）测距中误差；li为导线各边水平边长；mβ为导线等精度测角时的（单程）测角中误差。

图1 井下支导线

为分析研究方便，假设导线曲折度不大，βi近于180°，导线边长li大致相等，即为近于等边直伸形的复测支导线时［1］，则有

导线全长L＝l1＋l2＋…＋ln≈nl．

k点横向误差

k点纵向误差

设想一近于等边直伸形的往返复测支导线，各边长l，按光电测距仪的标称精度mD＝±（0．005＋5×10－6D），求得边长l单程测距中误差ml＝±（0．005＋5×10－6l），取 mβ＝±7″，mα0＝±9″，T＝2。当导线按3种不同边长（50 m，100 m，150 m）分别施测时，终点k的纵横向误差由式（1）、式（2）算得的结果列于表1中。

表1 等边直伸形支导线纵横向误差计算

表1中，全长L的导线：nl为边长l时的导线边数；μl为边长l时的导线横向误差；tl为边长l时的导线纵向误差。

由式（1）、式（2）和表1结果表明，必须设法控制横向误差的迅速扩大。首先应注意提高测角精度，增大导线边长有利于达到或提高导线水平角观测精度；同时，适当增大导线边长，意味着导线边数（测站数）的减少，体现在测量外业工作量的大幅度减少和导线精度的提高；其次可以在导线中加测陀螺定向边［2］（方向附合导线）来控制。

1．2 加测一条陀螺定向边及其最佳加测位置

如图2所示，由起始点B和起始边AB（坐标方位角为α0）开始测设了往返复测的支导线至终点k。如果仅在第nI条导线边上加测陀螺定向边，其坐标方位角为αI，这样便形成了两段导线：第1段，有nI条导线边构成方向附合导线，其重心为OI；第2段，有m条导线边构成支导线；导线总边数n＝nI＋m。

第1段导线按方向附合导线平差［3－4］后，终点k的点位中误差

式中：εi为第1段方向附合导线中各导线点与其重心OI连线长度（i＝1，2，…，nI）；Rj为第2段支导线中各导线点与终点k连线的长度（j＝1，2，…，m）；ROI为重心OI与终点k连线的长度；mαI为加测的陀螺定向边坐标方位角中误差；其余符号意义同上。

为了便于研究，设想导线为一近于等边直伸形的往返复测支导线，mα0＝mαI＝mα，导线各点（左）转折角作等精度观测，导线各边长li≈l，则导线终点k的点位中误差

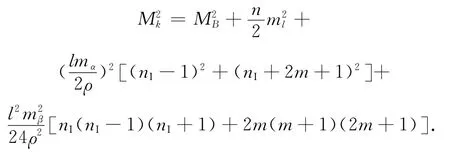
式中：mβ为导线等精度测角时的（单程）测角中误差；ml为导线各边（单程）测距中误差。

由上式可知：如何选择nI与m，在满足nI＋m＝n的条件下，使M2k有极小值［5］，这样就存在着陀螺定向边最佳加测位置的确定。

现设 f（nI，m）＝M2k，

则拉格朗日辅助函数

其中λ为某一常数。

根据多元函数条件极值的拉格朗日乘数法，则有

由式（3）、式（4）得

由式（5）nI＝n－m ，代入式（6），经整理后得

根据一元二次方程的实数解—求根公式法，则有

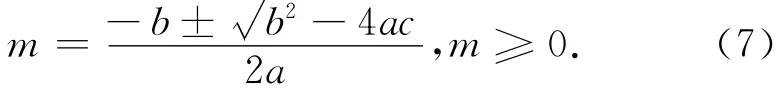
这里n为确定的值，取mβ＝±7″，mα＝±9″，由式（7）来计算m，nI＝n－m计算nI，结果列于表2中。

为研究方便，可忽略导线起始点B误差的影响，按陀螺定向边加测位置的最优解所确定的nI和m值（取整数）来计算，则导线终点k的最小点位中误差

取l＝150 m，ml＝±（0．005＋5×10－6l）＝±0．005 8 m，由上式计算 Mkmin，结果也列于表2中。

从表2和表1可知：导线总边数n≤5时，陀螺定向边加测在末边上；否则，定向边随总边数的增加由末边开始上移，直到1／3总边数的位置；导线终点点位中误差可减小0．5～1．5倍。

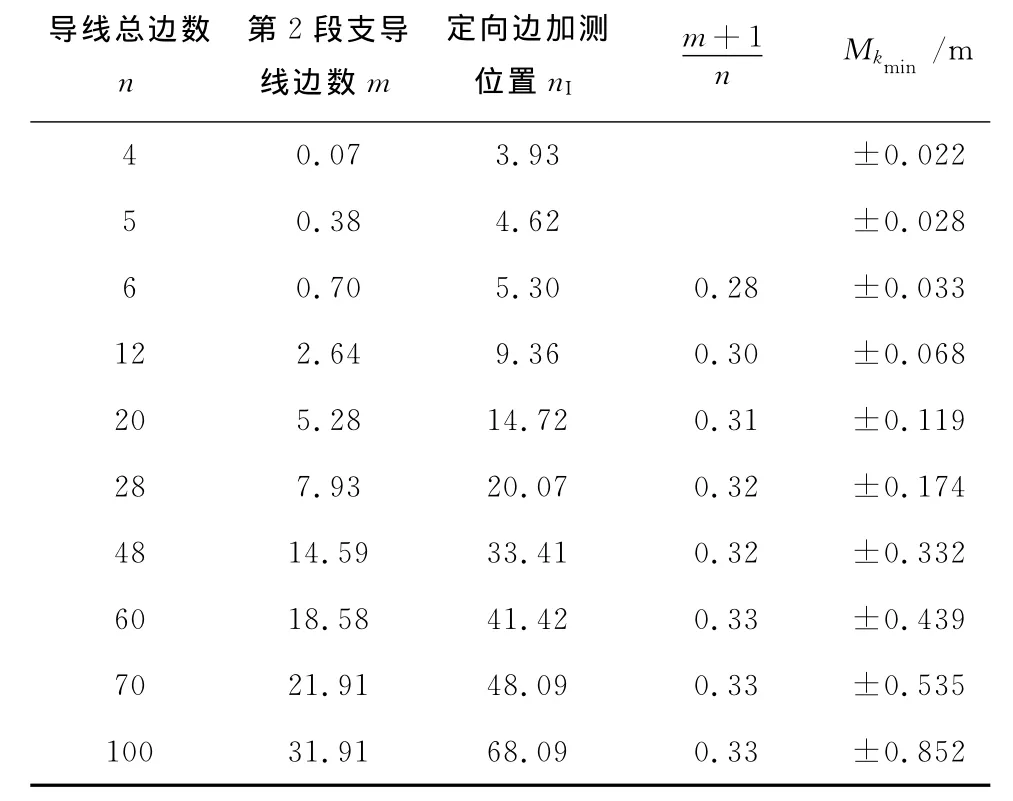
表2 陀螺定向边加测位置的最优解与导线终点中误差计算

1．3 加测多条陀螺定向边成为多节导线

导线或导线网中最基本的单元是导线节，所谓导线节就是两端都有坐标方位角控制的一节导线。

如图2所示，由起始点B和起始边AB开始已测设了往返复测的支导线至终点k，并在导线中每隔一定距离加测陀螺定向边，共加测了N条陀螺定向边，其坐标方位角分别为αIαIIαN从而形成（N节）多节导线。各导线节的重心分别为OI，OII，…，ON，则当角度按多节导线（方向附合导线）平差后，导线终点k的点位中误差［6］

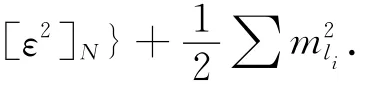
式中：mαi为各条陀螺定向边坐标方位角中误差；Ri－j为i点与j点连线长度；ε为各导线点与本节导线重心O连线长度，详见图2中虚线所示；其余符号意义同上。

图2 加测多条陀螺定向边的多节导线

井下导线起始边AB坐标方位角α0和各条陀螺定向边坐标方位角均采用JT15陀螺经纬仪独立定向两次取其平均值而得到。陀螺经纬仪定向遵循以下规则：3—2—3，即地面（下井前）测定仪器常数3次—井下定向边测定陀螺方位角2次—地面（上井后）测定仪器常数3次。

地面测定仪器常数和传递坐标的地面连接测量都共用同一近井点后视边（已知边）时，可忽略MB和不考虑近井点后视边的坐标方位角误差影响，则陀螺定向边坐标方位角中误差

式中：nΔ为地面测定仪器常数次数，取6；n下为井下定向边测定陀螺方位角次数，取2；mΔ为地面一次测定仪器常数中误差；mT为井下一次测定陀螺方位角中误差，取±15″。

由于起始边和各定向边的坐标方位角都为同一台陀螺经纬仪采用一样的定向方法而求得，则有mα0＝mαI＝ … ＝mαN＝mα。

为了便于说明问题，设想一近于等边直伸形的往返复测支导线改造成为多节导线，等距离间隔加测陀螺定向边［7］，共加测了N条，限于篇幅，不经推导而直接给出终点k的纵横向误差计算公式［8－9］如下：

横向误差

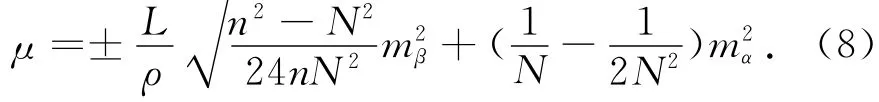
纵向误差

终点k的点位中误差

这里n为多节导线总边数，n＝nI＋nII＋…＋nN；导线各边长li≈l；导线全长L≈nl；mli≈ml。

进一步用数据说明加测陀螺定向边对减少横向误差μ的作用，并与纵向误差t作对比，设有多条（2条）近于等边直伸形多节导线（第1条：li≈l＝150 m，n＝28，L≈nl＝4 200 m；第2条：li≈l＝150 m，n＝48，L≈nl＝7 200 m ），mβ＝±7″，mα＝±9″，ml＝±0．005 8 m。用μβ和μα表示由mβ和mα引起的横向误差，于是按加测陀螺定向边数N ＝2～6，根据式（8）、式（9）、式（10）来计算各项误差，计算结果见表3和表4。

表3 等边直伸形N节导线终点误差计算（L＝4 200 m）

表4 等边直伸形N节导线终点误差计算（L＝7 200 m）

从表3和表4中可看出：测角误差影响项μβ随N的增大而迅速减少，但坐标方位角误差影响项μα的减小显得缓慢些；当N＝3和N＝4时，μ减小明显，其后就不太显著了，因此，在加测的陀螺定向边坐标方位角精度不能提高的条件下，过多地加测陀螺定向边收益并不太大，而加测陀螺定向边所增多的工作量很大；结合表1可看出，多节导线的纵向误差与支导线的一样，而点位中误差总比相应的支导线小许多，终点精度一般可提高1．6～4．5倍。

1．4 陀螺定向—光电测距导线

该导线采用陀螺经纬仪测定每条边的坐标方位角，再利用支导线往返复测时由光电测距仪测定的每条导线边长。为了检查陀螺经纬仪是否处于正常状态和提高测定仪器常数的精度，需要在每天下井前和上井后测定仪器常数。然后求出仪器常数的平均值，用来计算当天所测的井下一组边（或称为“分段”各边）的坐标方位角。

陀螺经纬仪定向仍遵循前面的规则，即3—2—3。各组（段）导线边坐标方位角均采用同一陀螺经纬仪独立定向两次取其平均值而得到。

如图3所示，测量了各边的坐标方位角αji及边长lji，j表示采用同一仪器常数的段号，j＝1，2，…，N ；i表示每段中导线的边号，i＝1，2，…，nj。

图3 陀螺定向—光电测距导线

在地面和井下的一次陀螺方位角测定均采用同一陀螺经纬仪和相同的作业方法，则导线终点k的点位中误差

式中：mlji为各导线边单程光电测距中误差；mα0上为地面测定仪器常数时所用的同一已知边（近井点后视边）坐标方位角中误差；RBk为导线起点B到终点k点连线长度；Rj为各段导线的起点到该段的终点连线长度；其余符号意义同上。

设有一近于等边直伸形陀螺定向—光电测距导线，各边长lji≈l＝150 m，总边数n＝28，全长L≈nl＝4 200 m，mT＝±15″，ml＝±0．005 8，nΔ＝6，n下＝2。

地面测定仪器常数和传递坐标的地面连接测量都共用同一近井点后视边时，可忽略MB和不考虑近井点后视边的坐标方位角误差影响，则终点k误差如下：

横向误差

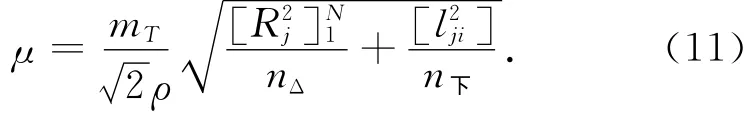
纵向误差

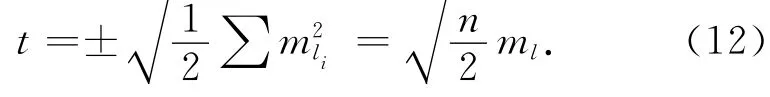
点位中误差

当导线等分为N段施测时，由式（12）、式（13）、式（14）来计算，结果见表5。

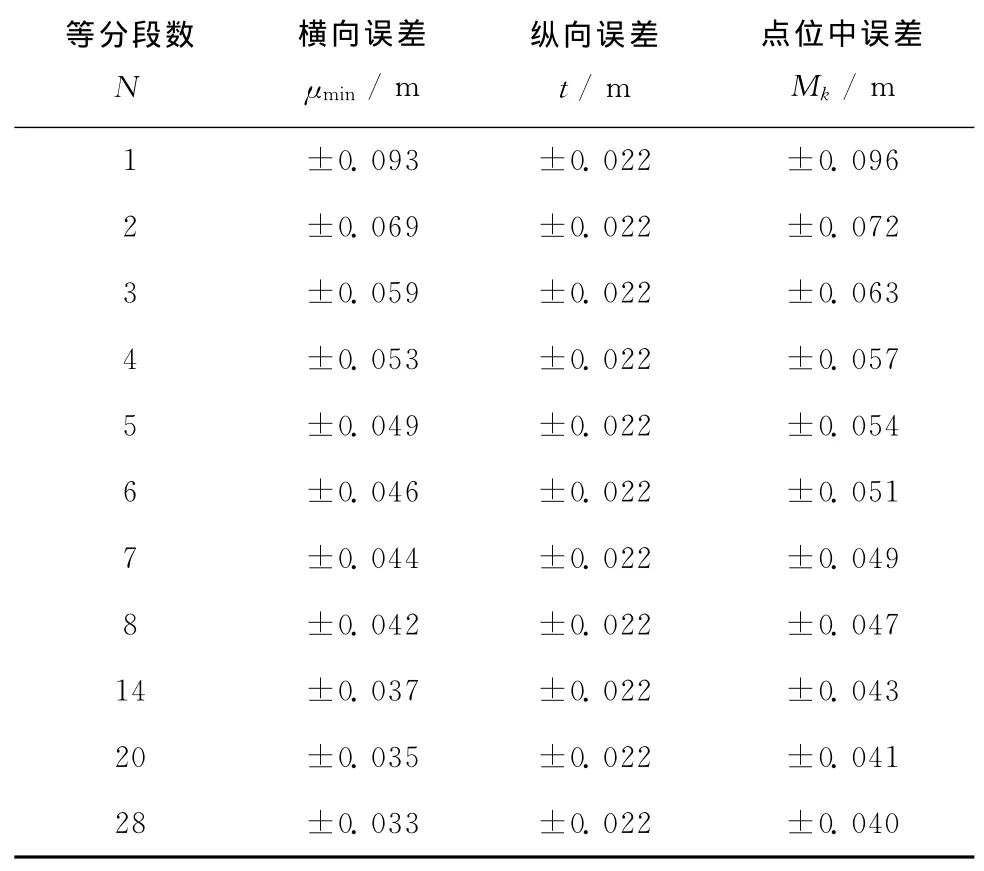
表5 等边直伸形陀螺定向—光电测距导线终点误差计算

根据Rj优化选择（Rj＝）和表5可知：横向误差都不太大了，随着等分段数N增大而缓慢减小；纵向误差不随N变化；过多的等分段数（增大N）实际意义不大，N可在2～4中选取，也可酌情任意选择；等分段数N确定后，各段导线长度（或边数）应大致相等。

由表5和表1可知，采用陀螺定向—光电测距导线的点位精度总比支导线的高许多，一般能提高3～8倍。

2 结 论

1）井下支导线中加测一条陀螺定向边的最佳加测位置：导线边数较少（n≤5）时，加测在末边上；否则，定向边由末边开始上移至导线总边数1／3的位置。导线终点点位精度可提高0．5～1．5倍。

2）加测多条陀螺定向边时，可等距离间隔加测陀螺定向边而改造成为多节导线，一般能提高终点精度1．6～4．5倍。但过多地加测陀螺定向边收益不大，以加测3～4条定向边为宜。

3）对于井下支导线中加测每条边的陀螺方位角而成为陀螺定向—光电测距导线，其终点误差显得很小了，较支导线的点位精度一般能提高3～8倍，仅在超长距离或超高精度的矿山贯通工程测量中应用。同时应当尽量采用地面连接测量中的近井点后视边（已知边）来测定仪器常数，便于消除地面起始方位角误差对贯通的影响。

［1］ 孔祥元，郭际明．控制测量学［M］．3版．武汉：武汉大学出版社，2011：48－49．

［2］ 张正禄．工程测量学［M］．2版．武汉：武汉大学出版社，2013：321－331．

［3］ 刘长星．加测陀螺定向边后方向附合导线的平差［J］．西安科技学院学报，2001，21（4）：340－343．

［4］ 程飞，张丽娜，赵志红．导线加测陀螺方位角的过程简化探讨［J］．测绘工程，2014，23（6）：56－58．

［5］ 同济大学数学系．高等数学［M］．6版．北京：高等教育出版社，2009：109－118．

［6］ 张国良，朱家钰，顾和和．矿山测量学［M］．徐州：中国矿业大学出版社，2008：228－231．

［7］ 潘国荣，王穗辉．地下导线加测陀螺边最优位置确定及精度分析［J］．同济大学学报，2004，32（5）：656－659．

［8］ 武汉测绘学院控制测量教研室，同济大学大地测量教研室．控制测量学（上册）［M］．北京：测绘出版社，1995：354－363．

［9］ 中国华冶科工集团有限公司．YB／T 4385－2013冶金矿山井巷工程测量规范［S］．北京：冶金工业出版社，2013．