基于SVM的高耸圆形建筑物沉降数据分析及预报研究

杨 帆，郭正一，张子文

（辽宁工程技术大学，辽宁 阜新123000）

高大建（构）筑物在生活、生产中愈来愈多的出现，例如：高塔、烟囱、摩天大厦、风力发电机、电视信号塔等。正常情况下，高大建（构）筑物要承受自重、风向、温度、季节性湿度、光照、地质条件等影响，极大可能会出现变形，诸如水平位移、沉降、倾斜、扭曲、张裂等。所以在施工及运行中均要求对高大建（构）筑物进行连续监测。若其中某些变形量超过其结构能够承受的范围，则导致高大建（构）筑物的倒塌，损失巨大，后果将不堪设想。很多监测指标中，沉降监测作为最重要的一项，对建（构）筑物进行沉降监测是建（构）筑物安全运行的必要措施之一。实验数据获取、处理方式为：对河北某电厂烟囱进行沉降监测，并作出预测可靠性对比。

1 基本模型

1．1 变形体基本情况

观测烟囱位于河北某电厂内东南方向，该烟囱为钢筋砼结构，总高度210 m，底直径19．2 m。基础为园形板式基础，底标高为－5．0 m；基础砼标号为C30，筒身为双层双向配筋。坡度±0．00～＋110．00 m为2．0%，其余部分坡度为0。烟囱壁厚度由下而上分别为380～180 mm。烟囱内衬采用泥砌粘土制耐火砖，筒壁隔热层采用厚度为100 mm水泥珍珠岩制品和80 mm厚珍珠岩粉。外筒壁由2．55 m开始设钢爬梯，标高103．500 m设信号平台。自烟囱筒壁顶端向下延生30 m以内，每5 m为一段刷两遍红白相间的涂刷航空标志漆。

数据获取使用的仪器为TOPCON DL－101C电子水准仪及其配套使用的条码式铟钢尺，使用的仪器设备已经过国家认证测绘仪器检定部门检定合格。同时测量前对基座及水准气泡均进行了校正，达到《建筑变形测量规范》要求，测量数据均进行了验证，完全符合沉降数据精度要求。通过测量得出一系列的观测数据，观测烟囱示意图及点位布设如图1所示。

1．2 小波去噪

1．2．1 基本原理

在小波分析应用中，降噪是其在信号处理领域的一个重要用途之一。而正交小波中，由于选取了正交基，比传统方法更接近实际信号本身，通过运用小波变换可以更容易地从原始序列中分离出信号部分和噪声部分。传统降噪方法的不足之处在于使信号变换后的熵增高，无法得到信号的相关性，同时也无法刻画信号的非平稳特性［1］。振动信号的噪声一般可以分为白噪声和有色噪声两大类。在降噪过程中，对于有色噪声的消除，一般采用首先对有色噪声白色化，然后再按照白噪声的消噪方式进行处理。因此，消噪研究的重点是如何消除信号中的白噪声。一个含有噪声的一维信号的模型可以表示成如下的形式：

式中：fn为真实信号，en为噪声，Xn为含噪声的信号。

在实际工程应用中，有用的信号通常表现为低频信号或是一些比较平稳的信号，而噪声信号则通常表现为高频信号。所以消噪过程可按如下方法进行处理：首先对信号进行小波分解，根据小波分解的特点，将信号分为低频段和高频段，则噪声部分通常包含在高频段中，因此对高频段以阈限域值等形式对小波系数进行处理，这种处理符合噪声在高频部分均匀密集的特点［2］。

1．2．2 连续小波变换

对 ∀f（t）∈L2（R），f（t）的连续小波变换（有时也称为积分小波变换）定义为

或用内积形式

式中

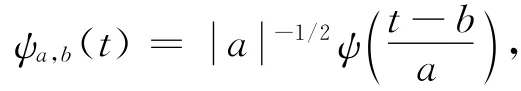
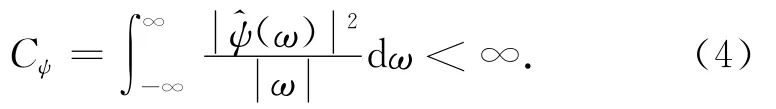
Cψ这个常数限制了能作为“基小波（或母小波）”的属于L2（R）的函数ψ的类，尤其是若还要求ψ是一个窗函数，那么ψ还必须属于L1（R），即

从式（6）可以发现小波函数必然具有振荡性。

连续小波变换具有如下性质［3］：

性质1：线性。即：设f（t）＝αg（t）＋βh（t），则

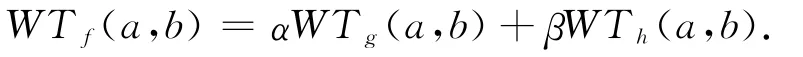
性质2：平移不变性。即：若f（t）↔WTf（a，b），则f（t－τ）↔WTf（a，b－τ）。平移不变性是一个很好的性质，在实际应用中，尽管离散小波变换要用得广泛一些，但在需要有平移不变性的情况下，离散小波变换是不能直接使用的。

性质4：冗余性。即：连续小波变换中存在信息表述的冗余度。其表现是由连续小波变换恢复原信号的重构公式不是唯一的，小波变换的核函数ψa，b（t）存在许多可能的选择。尽管冗余的存在可以提高信号重建时计算的稳定性，但增加了分析和解释小波变换的结果的困难。

面临离散数据情况下，要将连续小波离散化，用于更合理数据离散处理。

1．2．3 连续小波变换的离散化［4］

假定ψ是一个R函数，那么存在L2（R）的一个唯一的 Riesz基 ｛ψj，k｝j，k∈Z，它在以下定义上：〈ψj，k，ψl，m〉＝δj，lδk，m；j，k，l，m ∈Z，与｛ψj，k｝对偶。这时，每个f（t）∈L2（R）有如式（7）的唯一级数表示为

特别地，若｛ψj，k｝j，k∈Z构成L2（R）的规范正交基时，有ψj，k＝ψj，k重构公式为

利用小波变换分解沉降数据，经过重构数据，结合时间序列也可以进行创建预测模型［5］。但本文主要采用支持向量机进行创建预测模型。

1．3 不确定性支持向量机

1．3．1 基本原理

支持向量机是由Vapnik领导的AT＆TBell实验室研究小组在1995年提出的一种新的非常有潜力的分类技术。SVM是一种基于统计学习理论的模式识别方法，应用于模式识别领域。解决了机器学习方法的研究遇到一些重要的困难，比如如何确定网络结构的问题、过学习与欠学习问题、局部极小点问题等，使得SV M迅速发展和完善，在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中［6］。该理论针对小样本问题建立了一套新的理论体系，在这个理论体系下的统计推理规则不仅考虑了对渐进性能的要求，而且追求在现有有限信息的条件下得到最优结果

SV M的主要思想是建立一个超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。SV M的优点：通用性（能够在各种函数集中构造函数）；鲁棒性（不需要微调）；有效性（在解决实际问题中属于最好的方法之一）；计算简单（方法的实现只需要利用简单的优化技术）；理论上完备性（基于VC 推 广 理 论 的 框 架）。Kar ush－Kuhn－Tucker（KKT）约束规是起作用的约束的梯度与等式约束梯度线性无关，并且能使相应的优化问题成为凸问题，不涉及局部最优，以上特征和非零参数减少使得这套算法和神经网络算法有明显不同。

支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的。所谓VC维是对函数类的一种度量，可以简单理解为问题的复杂程度，VC维越高，一个问题就越复杂［7］。下面阐述基本原理：

最优化约束问题：

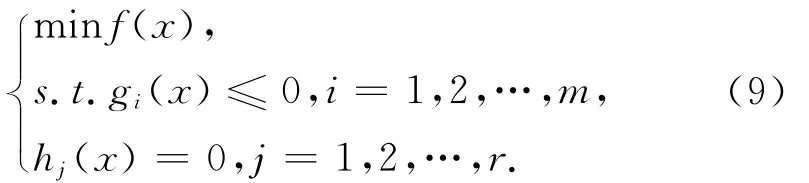
其中，f：Rn→R1（i＝1，2，…，m）；hj：Rn→R1（j＝1，2，…，r），设R ＝ ｛x：gi（x）≤0，i＝1，2，…，m；hj（x）＝0，j＝1，2，…，r；x∈Rn｝。

KKT必要条件：设x＊是问题（9）的可行解，f，gi（i∈I）在x＊处可微，gi（i∉I）在x＊处连续，hj（i＝1，2，…，r）在 x＊处 连 续 可 微。再 假 设▽gi（x＊），（i∈I）和 ▽hj（x＊），（j＝1，2，…，r）线性无关，如果x＊是问题（9）的局部极小点，则存在不全为0的ui（i∈I）和vj（j＝1，2，…，r），使得式（10）成立。

KKT充分条件：设x＊是问题（9）的可行解，f，gi（i＝1，2，…，m）是线性函数且在x＊处可微，hj（j＝1，2，…，r）是线性函数，如 果 存 在u＊i≥0（i＝1，2，…，m）和vj（j＝1，2，…，r），使得式（11）成立，则x＊是问题（9）的全局极小点。

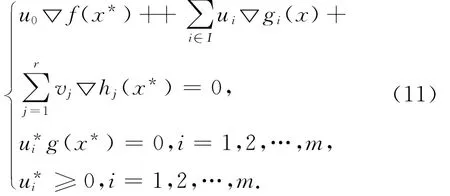
于是，应用KKT约束条件就可以求出最优超平面。SVM的主要思想是求出一个最优超平面，使得正例和反例之间的隔离边缘达到最大化。这里不给出最优超平面的求法。许多学者对SV M做出了分类算法改进，以LIBSV M作为最优改进模型。

1．3．2 LIBSVM 原理

在支持向量机的基础之上，许多学者通过调节或者改变某些函数项、系数或者变量，使得调节后公式在某些方面优势突出。LIBSV M算法采取了结合SMO算法和SV Mlight算法的突出优点，选取工作集满足SV Mlight工作集选取条件，选取好工作集后应用SMO两点优化方式，同时LIBSV M算法还采用了缓存和收缩技术。这样使得LIBSV M具有很好的性能，经过不断完善后被很多研究机构作为训练算法。

LIBSV M可以解决分类、回归、分布估计等问题。可以有效地应用在回归估计中。LIBSV M要求把样本的特征按照一定的格式表示。当输入向量中各个变量数量级相差过大会影响训练结果。为了避免此现象，调用scale模块对训练数据和测试数据进行归一化处理，归一化区间一般设置为［－1，1］。

2 数据处理及结果

2．1 小波去噪

本实验自2008年1月5日至2011年1月5日，每月等间隔观测1次，共36次观测。得出烟囱基座6个点的下沉值。本实验以1号观测点作为处理实例。观测值列表1。

应用db小波基对数据进行五层分解，处理后结果如表2和图2所示。

表1 原始观测下沉量

表2 去噪后数据

图2 去噪前后对比

2．2 libsv m预测

在MATLAB平台下，SV M工具箱种类很多，公认的最好用的是台湾大学林智仁的libsv m工具箱，本文主要应用libsv m工具箱做实验。具体实验步骤为：①选定训练集合测试集。实验中，采取去噪后信号前三分之二作为训练集，后三分之一作为测试集。②规范化。所有数据必须在同一规范集合中。③特征提取。特征提取也称作标签识别，对数据属性进行识别。④利用训练集训练分类器得到理想model，得到训练集的分类器。⑤利用model对测试集进行预测。⑥对分类器性能评测，得到分类器准确率进而评价预测准确性。实验中，采用原始数据和预测数据的标准差作为预测结果好坏的指标。

利用工具箱中的sv mtrain、sv mpredict、sv mmse来训练实验样本、预测结果、求出均方差。处理结果如下：

数据中前26个是训练样本数据，训练均方误差为9．527 68e－03，后10个数据是预测结果，均方差为0．097 669 3，结果如图3所示。与遗传算法相比，小样本条件下，支持向量机更具有鲁棒性［8］，学习和预测更准确。

图3 SVM预测结果

2．3 实验结果

由实验表明，经过小波降噪后得到下沉数据，再经libsv m进行学习和预测可以得到较高可信度的结果。不确定性支持向量机的预测结果和学习效果比遗传算法可靠，可及时发现不均匀下沉。但是其中有3个问题：①下沉量随季节和风力影响未作出相应定量研究。②机器学习沉降数据的样本量总体较小，极可能导致学习不充分，带来预测结果不准确或者精度低。③本实验采用均方差为评价指标有合理性及不合理性，在统计学评价标准层面上合理，但是应有其他评价指标一同检验预测结果。

3 结 论

1）用同样方法处理烟囱基座的6个点，得出：烟囱6个观测点总体下沉均匀，且在允许沉降范围内，即烟囱未发生倾斜。说明施工地基处理合理，工程质量过关。

2）预测方法可靠。高大建筑物下沉是连续性的，观测数据是间断性的，所以结合试验得出：通过小波降噪处理后得到观测结果是合理的，小样本情况条件下，应用支持向量机进行学习和预测运算简单，结果可靠。

3）建（构）筑物监测过程中，面临监测点保护不完全，导致监测数据不完全。本基座有2个点观测过程中各有7期数据没有观测到，其中处理方法［9－11］有：①直接把未观测到数据赋予下沉量为0。②和相邻数据进行插值。本实验中采取第2种处理方式保证数据列的连续性和时间序列的一致性。

［1］ 潘国荣，谷川．变形监测数据的小波神经网络预测方法［J］．大地测量与地球动力学，2007，27（4）：47－50．

［2］ 薛茄，毛灵涛，安里千．小波分析在动态实验数据处理中的应用［J］．湖南科技大学学报：自然科学版，2007，22（1）：59－62．

［3］ 郝文广，丁常富，梁 娜．小波降噪与FFT降噪比较［J］．电力科学与工程，2011，27（3）：59－61．

［4］ 高成．Matlab小波分析与应用［M］．2版．北京：国防工业出版社，2007．

［5］ 王祖顺，韩吉德．小波分解下的变形预报组合模型［J］．测绘工程，2013，22（4）：30－34．

［6］ Nello Cristianini，John Shawe－Taylor．支持向量机导论［M］．北京：电子工业出版社，2004．

［7］ 祥磊，赵新华．支持向量机在地面沉降预测中的应用［J］．山西建筑，2007，33（14）：4－6．

［8］ 郝长春．支持向量机在水库大坝变形中的预测分析［J］．黑龙江工程学院学报：自然科学版，2013，27（2）：8－12．

［9］ 罗红明，唐辉明，英鄂川．武汉阳逻电厂烟囱基础沉降预测研究［J］．岩土力学，2006，27（S2）：844－848．

［10］周吕，文鸿雁，韩亚坤．灰色预测与Kal man滤波在建筑物沉降变形分析中的应用［J］．测绘科学，2014，39（4）：149－151．

［11］刘严萍，张飞涟，王勇，等．北京近年地面沉降监测研究［J］．测绘科学，2014，39（10）：68－70．