一种基于谐振腔结构的微波位移传感器
谢兴娟
(中国航空工业集团公司 北京长城计量测试技术研究所计量与校准技术重点实验室,北京100095)
0 引 言
位移传感器作为一种常见的基本传感器,有很高的测量精度和广泛的应用。目前位移传感器进一步发展的主要的方向为测量精度的提高,体积的减小和能够适应更加特殊的工作条件和环境[1~3]。例如:航空发动机内部叶尖间隙的尺寸严重影响发动机的工作的效率和稳定性,但是由于其中高温、燃气、燃油污染等特殊的工作环境要求,需要一种特殊的位移传感器进行发动机内部叶尖间隙的测试[4~8]。微波介于无线电和可见光之间,具有很好的定向辐射和传输性能,能够穿透发动机中的污染介质,遇到金属障碍物反射,非常适用于航空发动机中叶尖间隙的测试[9,10]。
本文设计了一种基于谐振腔原理的位移传感器,传感器探头为开放谐振腔结构,能够通过谐振频率的改变进行位移的测试。此微波传感器能够承受高温、高污染等恶劣的工作环境,适合应用于航空发动机的叶尖间隙测试。通过对传感器内电场的计算分析完成了谐振腔工作模式选择,建立了工作在24 GHz 的微波传感器模型,分析了尺寸变化对工作频率的影响,通过模拟计算得到了在间隙0~6 mm内大于240MHz/μm 的测试灵敏度,验证了该设计的正确性。
1 设计原理
图1 为所设计的谐振腔结构微波传感器结构示意图,其主要结构是由金属壳体形成的谐振腔,谐振腔一端用金属短路面封闭,另一端开放正对被测目标。同轴电缆插入短路面,连接传感器探头与微波信号源以及后续测试电路。谐振腔内部设置一定的耦合结构连接同轴电缆,耦合结构能够在电缆和谐振腔前壁之间激励出磁场,为谐振腔提供馈电。
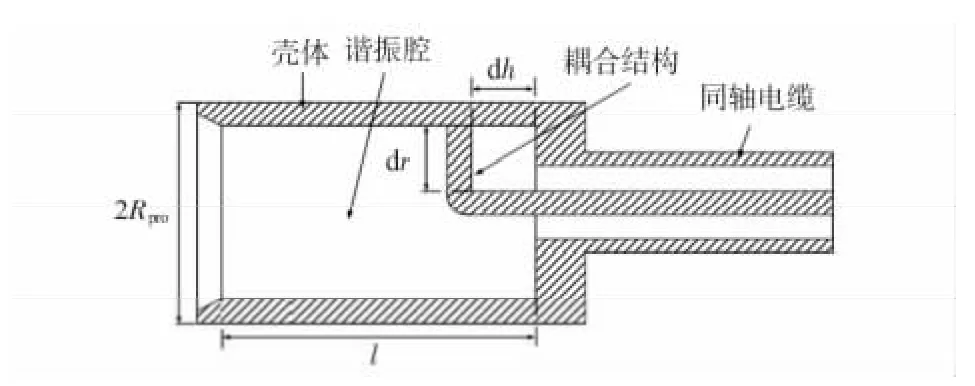
图1 微波传感器结构示意图Fig 1 Structure diagram of microwave sensor
微波传感器利用谐振腔谐振频率随位移距离的变化进行测试,其具体原理过程为:传感器探头和其开放端口正对的金属材料的被测目标形成一个空腔谐振器,当被测目标接近或离开开放端口时,此谐振器的谐振频率将受到影响。当空腔谐振器端口没有金属被测物时,等效于谐振腔内部尺寸变大,谐振频率降低,因此,谐振腔产生最低的频率谐振;当空腔谐振器端口放置金属被测物时,等效于谐振腔内部尺寸最小,谐振频率增大,此时将产生最高的频率谐振。比较高谐振频率和低谐振频率的变化差值,就可得到被测目标的位移值。此微波传感器中的谐振腔可以为矩形或圆柱形结构,这里以圆柱形谐振腔结构为例(图2),对传感器具体的电场分布和工作模式进行分析[11]。
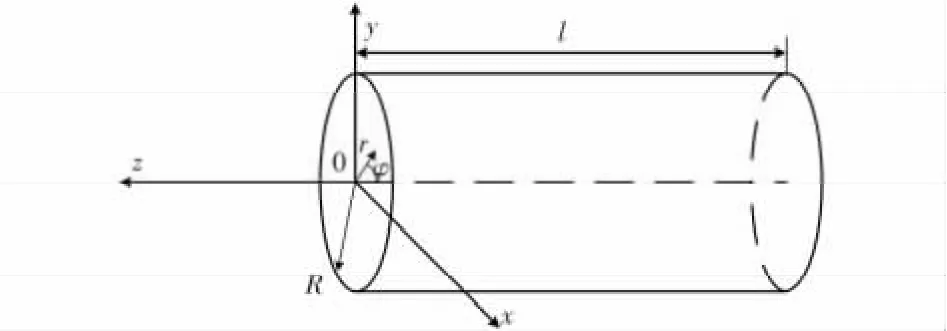
图2 圆柱谐振腔计算模型Fig 2 Calculation model of cylindrical resonant cavit y
图2 为圆柱形谐振腔计算模型,为一段内径为R 长度为l 的圆波导结构。首先假设谐振腔圆波导两端封闭,以圆波导中TEmn波为例,研究圆波导传输线沿z 轴方向的行波场。圆波导中TEmn的z 向磁场分布为

在z=0 处放置一块金属板,使得Hz=0 的全反射条件为
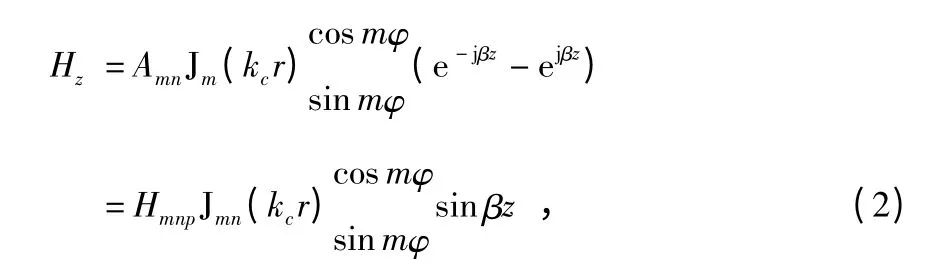
式中 kc=mmn/R,mmn是m 阶Bessel 函数导数的第n 个根。再在z=l 处放置一金属板,又一次构成Hz=0 的全反射条件
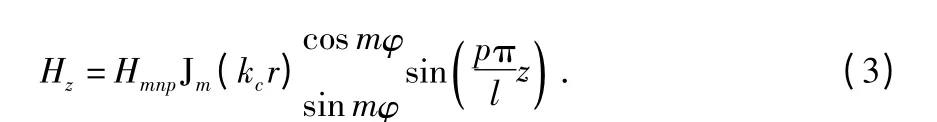
在波导中,横向分量用纵向分量表示得到不变量矩阵
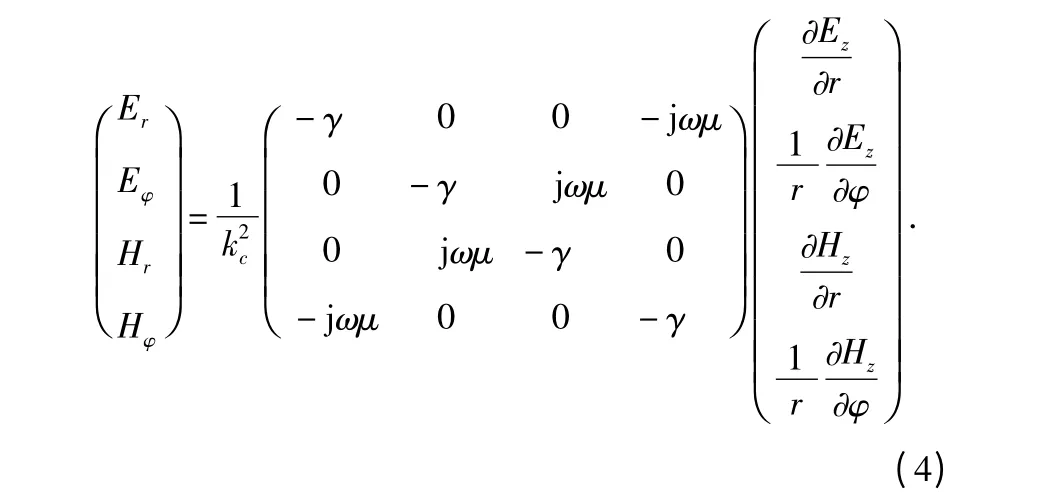
结合式(3),式(4)进一步计算,得到圆柱谐振腔中TEmnp模场表达式为

可见圆柱谐振腔中TEmnp模电场z 向分量为零,即谐振腔两端端面上无壁电流,因此,将谐振腔一端口开放对此模式的场分布影响很小,依然可以得到很高的Q 值,所以,选择所设计的微波传感器中谐振腔的工作模式为TEmnp。进一步分析可得圆波导TEmnp模的谐振频率f0计算公式为
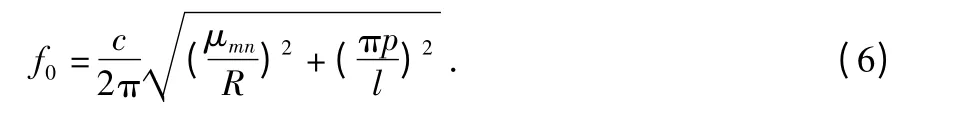
为了降低传感器本身在测试过程中对测量真实值的影响,要求传感器的径向尺寸尽量小,因此,选择波长最长的TE111模,其谐振频率公式为
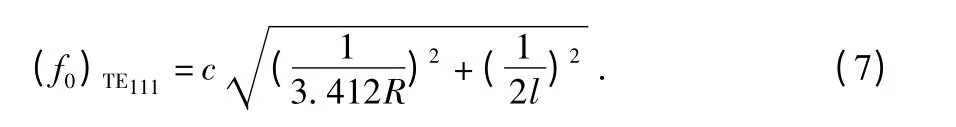
此公式体现了传感器谐振频率与探头实际尺寸之间的关系,也是进行传感器设计的理论依据。
2 模拟仿真
图3 为运用三维电磁场计算软件CST—MWS 微波工作室建立的谐振腔结构微波传感器的三维计算模型图。通过公式(7)可以得到谐振腔工作频率和谐振腔的结构尺寸之间的关系,在此基础上,通过计算机对模型的优化计算,最终获得工作在24 GHz 左右微波传感器模型,其探头外径尺寸为9 mm,长度约为13 mm。

图3 微波传感器三维计算模型图Fig 3 Three dimensional calculation model for microwave sensor
对谐振腔谐振频率的判断可以通过测试同轴电缆端口的反射系数S11频率曲线获得,在谐振频率点,由于传感器内部谐振存储了能量,使得反射回同轴电缆的反射信号很弱,表现为反射系数频率曲线上的最低峰值点。图4 为通过模拟计算得到的目标距离分别为0.2,1.6,3 mm 时传感器端口的反射系数幅值频率曲线。测试频率范围为22~26 GHz,图中反射系数曲线最小峰值点的变化体现了目标位移变化过程中引起的谐振频率的变化情况,可见随着目标距离的增大,传感器谐振频率降低,与之前的理论分析结论一致。反射系数峰值越低,传感器在此频率点的谐振能力越高,谐振腔Q 也越高,谐振腔Q 值与其群时延的关系公式为

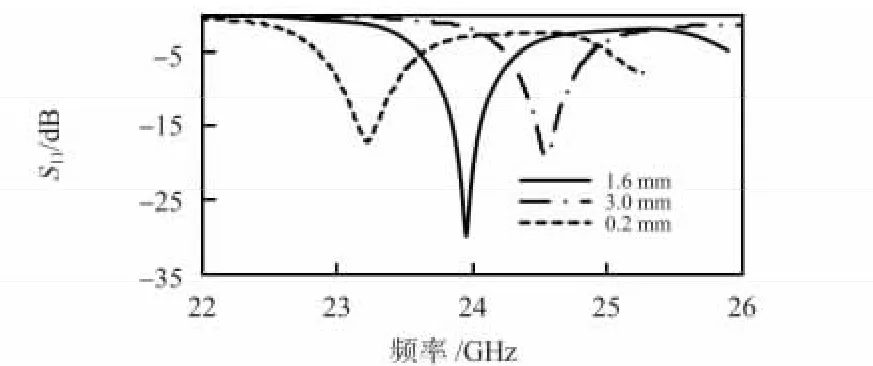
图4 微波传感器端口反射系数幅值频率曲线Fig 4 Curve of port reflection coefficient amplitude vs frequency of microwave sensor
图4 中被测目标距离在1.6 mm 处的反射系数峰值点最低,计算其相应的端口群时延曲线如图5 所示,其最高峰值点满足τg=18.523,带入公式(8)计算得此时的Q 值为698,说明传感器中的开放端口和材料、介质等其他因素引起的能量损耗都很少,大部分能量存储在谐振腔中。
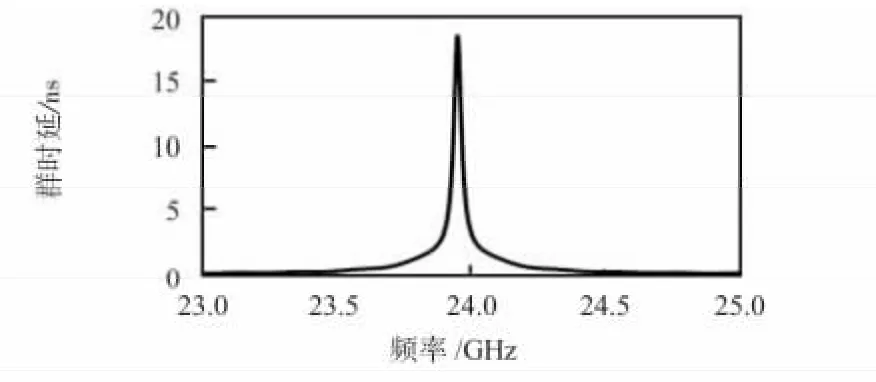
图5 位移1.6 mm 时的端口群时延频率曲线Fig 5 Curve of port group time delay vs frequency while displacement is 1.6mm
图6 为传感器在被测目标距离为1.6 mm 时,其谐振频率点23.952 GHz 处的谐振腔内部电场分布图,可见同轴电缆中传输的微波信号通过馈电结构顺利地耦合进圆柱谐振腔中,并在谐振腔中激起了很强的电场,谐振腔中的电场分布为TE111模式,模拟计算结果与设计目标相同。
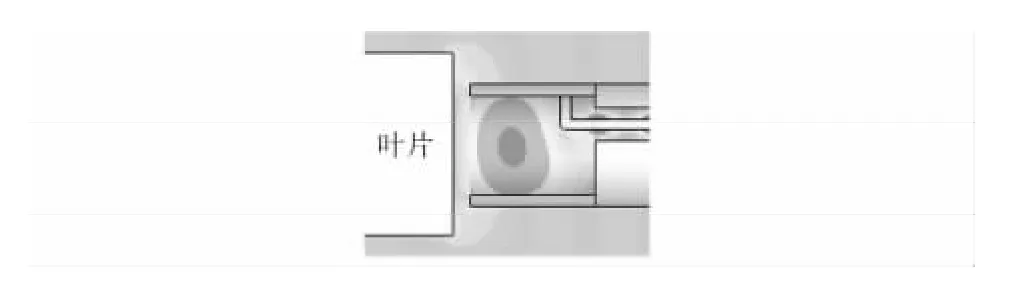
图6 传感器内部电场分布图Fig 6 Electric field distribution inside sensor
图7 为计算得到的传感器的尺寸偏差引起的传感器谐振频率变化曲线。可见影响谐振腔传感器的谐振频率最大的参数是谐振腔的内半径。谐振频率随着内半径值的增大而减小,这种现象与谐振腔理论匹配。因此,为了减小传感器设计结果与实物测试结果的误差,在实际加工过程中,对加工精度要求最高的结构参数是传感器谐振腔的内半径。但是同时由于传感器基于谐振频率变化的原理进行测试,在对实际传感器样件进行校准后,这种偏差不会影响传感器的测试精度。
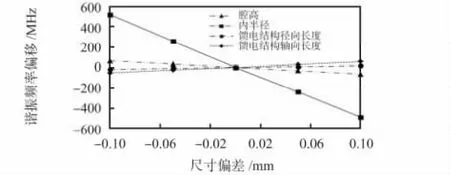
图7 传感器尺寸偏差引起的谐振频率的变化Fig 7 Resonant frequency change caused by size deviation of sensor
图8 为传感器的尺寸偏差引起的传感器反射系数幅值变化曲线,可见影响谐振频率点反射系数幅值的两个较大的结构参数分别是谐振腔内半径和传感器馈电结构径向偏移值,传感器馈电结构径向偏移0.1 mm 引起的反射系数幅值最大约为0.095,此时传感器内部结构造成的能量反射为总能量的0.25%,大部分微波信号能够通过传感器向外传输,因此,确定传感器内部加工尺寸偏差对传感器传输信号的性能影响不大。
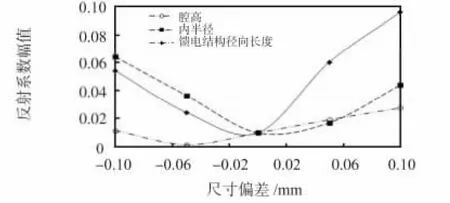
图8 传感器尺寸偏差引起的谐振频率点反射系数幅值的变化Fig 8 Amplitude change of reflection coefficient of resonant frequency point caused by size deviation of sensor
对用微波传感器进行位移测试进行模型计算,在传感器模型的开放端口前放置金属片,计算随着测量位移变化的端口反射系数最低峰值点频率的变化情况。其中金属端面为平行与传感器端口的矩形面,具体尺寸为长度16 mm,宽度为2 mm,矩形长边位置沿传感器水平极化方向。图9为针对此模型计算得到的谐振频率随测量位移距离变化曲线,可见测量位移在0~6 mm 变化范围内,谐振频率单调递减,从24.5 GHz 下降到22.5 GHz,变化范围约为2.4 GHz。
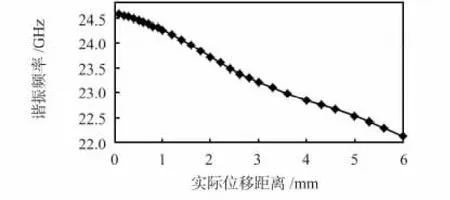
图9 传感器谐振频率随实际位移变化曲线Fig 9 Curve of resonant frequency of sensor vs actual displacement
图10 为计算得到的不同位移距离下微波传感器的测试灵敏度,假设在一小段位移内传感器为线性,再根据此段两端位移值下测量的频率值进行计算。可见在实际位移1.8~2.2 mm 内,传感器测试灵敏度最大,约为600 MHz/μm。在实际位移0.2 mm 处最小,约为240 MHz/μm。可见所设计的微波传感器,在位移变化范围0~6 mm 内,都能够保持很高的测量灵敏度。
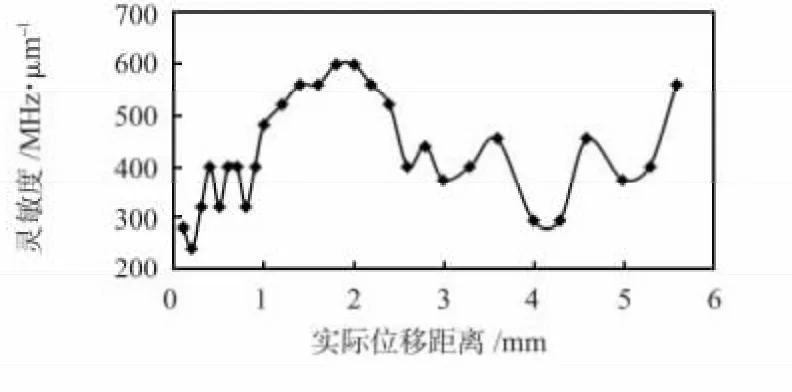
图10 微波传感器测试灵敏度随实际位移变化曲线Fig 10 Curve of test sensitivity of microwave sensor vs actual displacement
3 结 论
本文设计了一种基于谐振腔结构原理的微波传感器,其探头为开放式谐振腔,可以根据谐振频率的改变进行位移距离的测量。通过对传感器探头场分布进行分析完成了谐振腔工作模式选择,建立了工作在24 GHz 的微波传感器模型,通过模拟计算得到了在测量范围0~6 mm 内大于240MHz/μm 的测试灵敏度,验证了该设计的正确性。
[1] 昌学年,姚 毅,闫 玲.位移传感器的发展及研究[J].计量与测试技术,2009(9):42-44.
[2] 刘 亮.先进传感器及其应用[M].北京:化学工业出版社,2005:15-19.
[3] Jing Zhou,Min Ouyang,Yan Shen,et al.Liu study of a displacement sensor based on transmission varied-line-space phase grating[J].Optoelectronics Letters,2008(3):217-222.
[4] Holmquist Eric B.Turbine blade tip clearance measurement instrumentation[C]∥ASME Turbo Expo 2007,Montreal,Canada,2007:605-611.
[5] 张 娜,黄春峰.航空发动机叶尖间隙测量技术[J].航空制造技术,2010(13):41-45.
[6] 毕思明.燃气轮机叶尖间隙测量技术的研究[D].哈尔滨:哈尔滨工程大学,2011:2-15.
[7] 曹素芝.发动机叶片叶尖间隙非接触检测技术研究[D].天津:天津大学,2007:1-9.
[8] 熊宇飞.航空发动机转子叶尖间隙测量[J].测控技术,2004,23(1):5-7.
[9] Huang M,Yang J,Wang J.Microwave sensor for measuring the properties of a liquid drop[J].Measurement Science and Technology,2007(5):1934-1940.
[10]Wenger J,Noweck M,Stotz M.An mmic-based microwave sensor for accurate clearance measurements in aircraft engines[C]∥27th Microwave Conference,European,1997:1122-1126.
[11]李宗谦,余京兆,高葆新.微波工程基础[M].北京:清华大学出版社,2004:156-162.

