全自动酶免分析仪定量分析系统研究*
常海涛,祝连庆,王中宇,周哲海,郭阳宽
(1.北京航空航天大学 仪器科学与光电工程学院,北京100191;2.北京信息科技大学 光电测试技术北京市重点实验室,北京100192)
0 引 言
全自动酶免分析仪是临床检验必备的分析仪器,主要用于传染病血清学标志物、肿瘤标志物及内分泌等各种免疫指标的检测[1]。传统的酶免分析仪受限于其单色器滤光片组数量,只能进行定性分析。为实现定量分析,需采集样本全光谱数据,并借助于化学计量学方法,如,偏最小二乘(partial least square,PLS)[2]、主成分分析(principal component analysis,PCA)[3],建立光谱数据和待测样本属性之间的定量校正模型[4~6]。
近年来,遗传算法(genetic algorithm,GA)作为一种全局搜索方法,被广泛应用于组合优化、自适应控制[7]、图像处理[8]和光谱分析[9]等领域。特别是针对光谱分析中的波长选择问题,国内外学者的研究表明采用遗传算法进行波长选择,即可以剔除不相关变量、简化模型,又可提高模型的预测能力和稳健性[10]。但是遗传算法在使用过程中仍存在一些问题,如,“早熟现象”和种群进化效率低等[11]。
本文将多组分定量分析转化成组合最优化问题,提出了一种基于改进遗传算法的定量分析方法。通过自适应寻优空间和小生境技术加快种群的进化速度,提高算法的整体性能。以全息凹面光栅作为分光元件,搭建扫描式紫外可见分光光度计实验系统,并获得食品工业中最常见的苋菜红和胭脂红二组分混合水溶液的吸收光谱数据。
1 算法与原理
1.1 回归模型的建立
可见光谱数据通常呈多变量、强相关性,并与样本组分含量构成线性关系,符合朗伯比尔定律,即

其中,K 为吸收系数矩阵,mL/(μg·cm);b 为光程,cm;C 为样本浓度矩阵,μg/mL;A 为吸光度矩阵,n 为样本数,p 为测量波长数,m 为待测样本的组分数。由于建模用校正集样本的吸光度和浓度矩阵已知,而且样本数通常大于组分数,因此,可通过求超定方程最小范数最小二乘解的方法得到各组分的吸收系数。对浓度矩阵C 进行奇异值分解

其中,U 为n×n 阶列正交矩阵,S 为n×m 阶对角阵;V为m×m 阶列正交矩阵。吸收系数矩阵,即超定方程解为
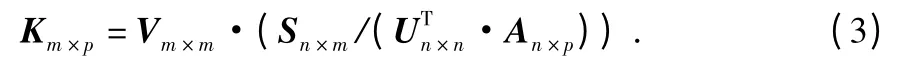
对于每一个待测集样本,利用遗传算法在浓度解空间搜索全局最优浓度解Cpred,带入到式(1),使得Cpred·K·b 等于或接近待测样本吸光度,Cpred即为待测样本的预测值。
1.2 遗传算法
遗传算法将达尔文“适者生存”理论引入到种群进化过程中,伴随着交叉、变异等遗传操作,实现种群中个体的信息交换,并不断产生出新一代更适合环境的种群,最后收敛于一个最适应环境的个体。本文采用的遗传算法操作参数设定为:二进制编码,种群规模40,选择算子采用随机遍历抽样,单点交叉(概率70%),变异概率1%,并采用精英主义策略保留最优个体。需要特别指出的是,本文选取待测样本预测吸光度曲线(即Cpred·K·b)和实测吸光度曲线的灰色综合关联度函数作为适应度函数。灰色综合关联度既考虑了吸光度曲线间的绝对位置变化,又兼顾了曲线自身的相对变化率,以综合集成的形式表征曲线间的相似程度[12],公式如下
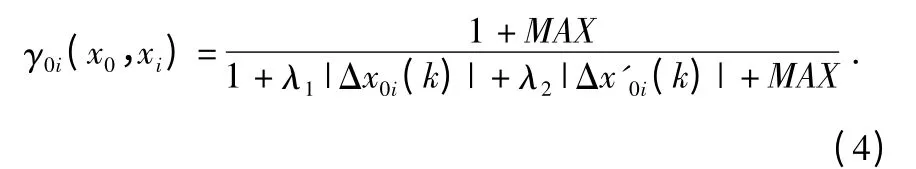
1.3 遗传算法的改进
1)自适应寻优空间:首先随机产生初始种群,计算个体适应度;然后以每代种群中最大适应度个体c0为中心生成下一代解空间[c0+d0,c0-d0],并在新的解空间中随机产生新的种群;重复上述操作,经过固定遗传代数,锁定搜索空间,引入选择、交叉、变异等遗传操作实现种群进化。
2)小生境技术:本文采用个体之间的广义海明距离作为共享函数,对相似个体中适应度较小的个体施加一个较强的惩罚函数,降低其适应度值,从而达到滤除相似个体,增加种群的多样性,加快收敛速度的目的。
2 实验系统搭建
2.1 分光光度系统
全息凹面光栅,具有像差校正、低杂散光和高信噪比等优点。以全息凹面光栅为核心的分光光度系统的结构如图1所示。
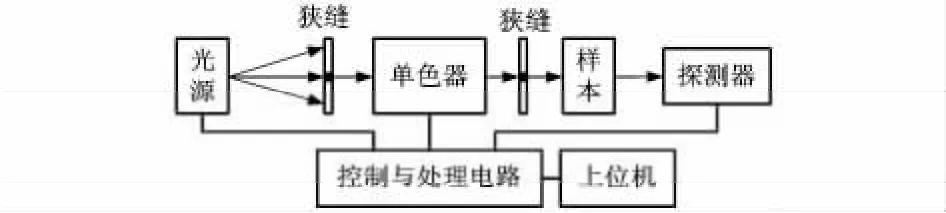
图1 分光光度系统框图Fig 1 Block diagram of spectrophotometer
从图1 可以看出:系统主要由光源、单色器、探测器、控制及处理电路和上位机组成。光源选用20 W 碘钨灯,辐射波长范围为320~800 nm,由于光源发热量大,采用外置结构,并配有散热片。单色器采用全息凹面光栅作为色散元件,与传统的C-T 结构光路相比,无需准直和聚焦成像系统,简化系统结构的同时减少光能量的损失。样本杯为1 cm见方石英材质的比色皿。探测器采用滨松R636—10 光电倍增管(光谱响应范围160~930 nm)。控制和数据处理部分,以TMS320F2812 DSP 为核心处理器,实现光源供电、光栅转台控制、探测器信号采集及处理和上位机数据传输与通信。需要指出的是,全息凹面光栅固定于可微调的光栅转接架上,确保光栅最凹处的切线与转台的中心轴线在一个平面上。步进电机驱动蜗轮蜗杆机构来带动光栅转台的连续转动,从而实现全谱段波长扫描。单色器实物如图2所示。

图2 单色器实物图Fig 2 Monochrometer
2.2 实验材料与方法
待测样本选用食品工业中最常见的苋菜红、胭脂红两种食用色素(国家标准物质研究中心提供)。采用精度为10 μL 手工加样器,吸取苋菜红和胭脂红纯组分标准溶液,分别置于100 mL 容量瓶中,用蒸馏水定容配制成两组分混合溶液,其中各组分浓度在0~200 μg/mL 范围内均匀分布,任意组合。选取蒸馏水为参比溶液,在波长381~630 nm(间隔1 nm)内,记录35 组混合色素样本吸收光谱数据,其中20 组作为校正集,15 组作为预测集。经Savitzky-Golay窗口移动多项式平滑后35 组混合色素样本吸收光谱如图3所示。从图3 可以看出:光谱曲线平滑,滤噪效果明显,并且苋菜红和胭脂红吸收峰接近,光谱重叠严重。
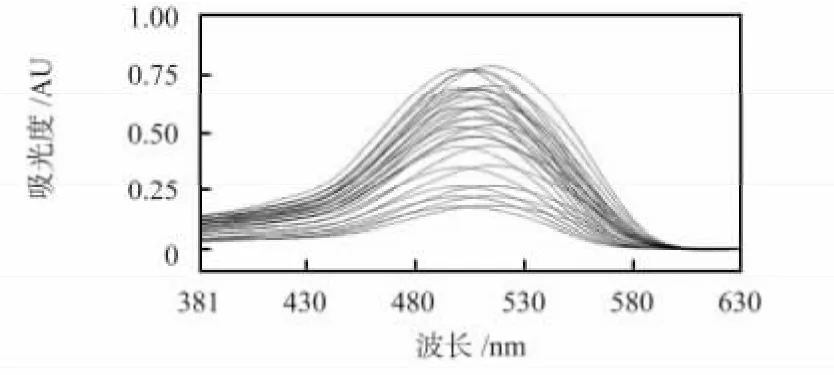
图3 平滑后苋菜红和胭脂红吸收光谱Fig 3 Absorption spectra of Amaranth and Carmine with smoothing
3 实验结果与讨论
3.1 吸收系数计算
将校正集样本吸光度和浓度矩阵带入到式(2)和式(3)中,通过解超定方程的方法计算苋菜红和胭脂红样本在不同波长点的吸收系数。为进一步验证吸收系数的准确性,将校正集样本浓度和两组分的吸收系数带入到公式(1),反推出校正集样本的吸光度Apred(预测吸光度),计算Apred和A(实测吸光度)中各样本数据序列间的灰色综合关联度。图4 给出了校正集20 个样本预测吸光度Apred和实测吸光度A 的灰色综合关联度变化曲线,其中二者的灰色综合关联度值均大于0.998,表明本文采用的解超定方程法求解样本吸收系数的准确度很高。

图4 Apred和A 的灰色综合关联度曲线Fig 4 Synthesized grey correlation(SGC)between Apredand A
3.2 划分寻优空间
以胭脂红(100 μg/mL)和苋菜红(80 μg/mL)混合样本为例,图5 给出寻优空间随遗传代数变化示意,边界变化值d0=5 μg/mL。由于胭脂红和苋菜红吸收峰接近,吸收光谱存在干扰,并且初始种群的解空间为[0,200],因此,生成的第一代寻优空间,可能并不包含最优解。自适应寻优空间技术能迅速定位全局最优解范围,本例中在第5 代寻优空间开始完全包含全局最优解,当遗传算法演化超过10 代时,寻优空间基本保持不变。最终胭脂红的寻优空间为[95.19,105.19],苋菜红寻优空间为[74.35,84.35],均包含全局最优解,且搜索空间缩小了20 倍。
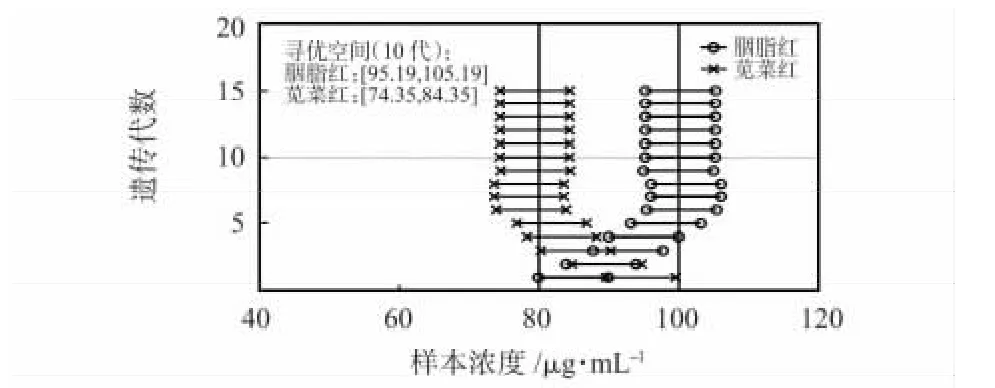
图5 寻优空间随遗传代数变化曲线Fig 5 Change curve of search space with evolutionary generations
3.3 算法比较
分别采用遗传算法和改进遗传算法对预测集样本浓度进行预测,以预测残差平方和(prediction residual error sum of square,PRESS)评价模型预测的准确性。图6(a),(b)分别给出了浓度为50&80,60&60,80&100,100&80μg/mL 的苋菜红和胭脂红混合样本,两种方法每代最优个体的PRESS 值随遗传代数变化曲线。
从图6(a)可以看出:遗传算法预测结果存在不确定性,由于早熟现象影响,a,b,d 样本经过1000 代进化仍收敛于局部最优解;c 样本经过69 代遗传进化收敛于全局最优解。改进遗传算法由于搜索空间进行了动态调整,每个样本均能迅速收敛于全局最优解。由图6(b)可知,4 个样本均在30 代以内收敛于全局最优解。
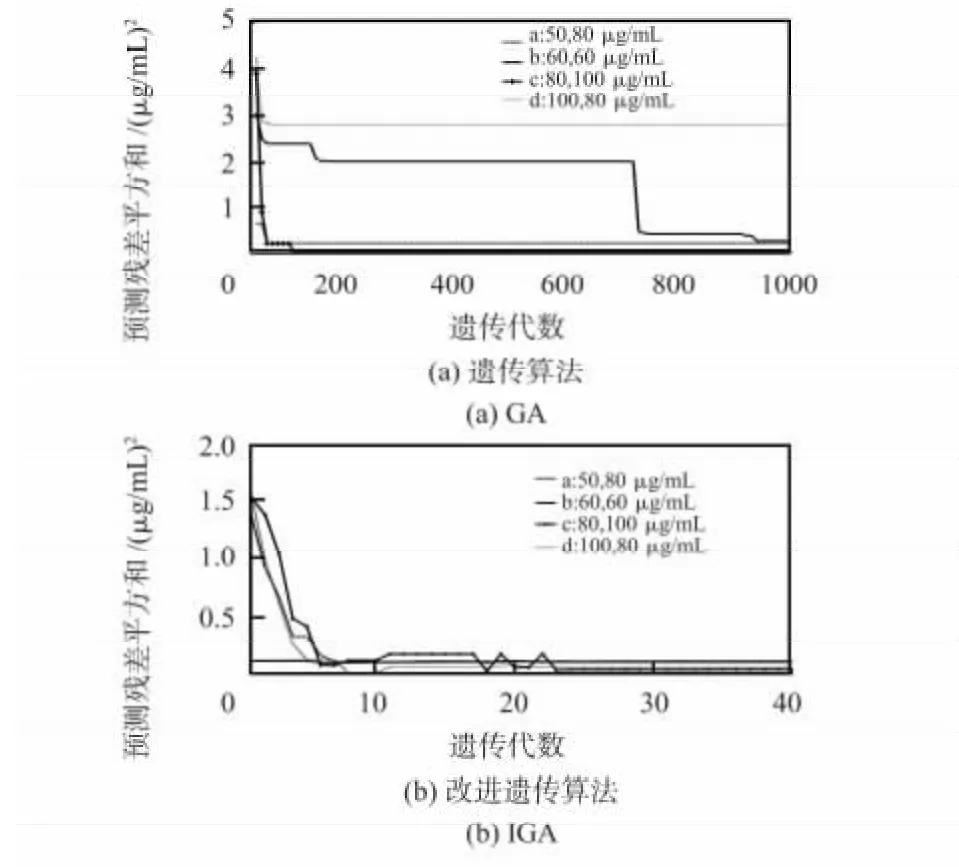
图6 遗传算法和改进遗传算法PRESS 值比较Fig 6 Comparison of PRESS by GA and IGA
采用校正集相关系数R 和预测均方根误差(RMSEP)对定量分析模型进行评价,并与传统的PLS 方法进行比较。由表1 可以看出:两种方法对苋菜红和胭脂红预测的相关系数和标准差基本相当。说明基于改进遗传算法的多组分定量分析模型具有较高的预测精度。
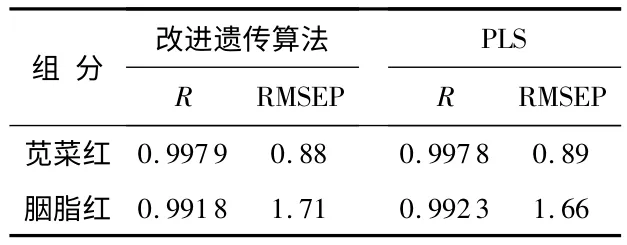
表1 改进遗传算法与PLS 预测性能比较Tab 1 Comparison of prediction performance index by IGA and PLS method
4 结 论
本文提出了一种基于改进遗传算法的多组分定量分析方法,将多组分定量分析转化成组合最优化问题,利用遗传算法在浓度解空间搜索全局最优浓度解。采用自适应寻优空间技术和小生境技术对传统遗传算法进行改进,一定程度上加快了遗传算法收敛速度,克服“早熟现象”。搭建以凹面全息光栅为核心的酶免分析仪分光光度系统,对食品工业中最常见的苋菜红和胭脂红混合溶液定量分析。其中苋菜红和胭脂红待测样本参考值与模型预测值间的相关系数R 分别达到了0.997 9,0.991 8,RMSEP 分别为0.88,1.71 μg/mL。实验结果表明:本文所研究的方法具有较高的预测精度,满足酶免分析仪定量分析的要求。
[1] Dilorenzo M E,Timoney C F,Felder R A.Technological advancements in liquid handling robotics[J].Journal of Laboratory Automation,2001,6(2):36-40.
[2] 乔晓艳,王艳景,李 刚.偏最小二乘法荧光光谱预测啶虫脒农药残留[J].光学精密工程,2010,18(11):2369-2374.
[3] Stanimirova I,Walczak B,Massart D L,et al.A comparison between two robust PCA algorithms[J].Chemometrics and Intelligent Laboratory Systems,2004,71:83-95.
[4] Lee S,Kim K,Lee H,et al.Improving the classiɦcation accuracy for IR spectroscopic diagnosis of stomach and colon malignancy using non-linear spectral feature extraction methods[J].Analyst,2013,138:4076-4082.
[5] Shao X G,Wang W,Hou Z Y,et al.A new regression method based on independent component analysis[J].Talanta,2006,69(3):676-680.
[6] Clavaud M,Roggo Y,Daeniken R V,et al.Chemometrics and inline near infrared spectroscopic monitoring of a biopharmaceutical Chinese hamster ovary cell culture:Prediction of multiple cultivation variables[J].Talanta,2013,111:28-38.
[7] Shen Z H,Zhao Y K,Wu W W.Niche pseudo-parallel genetic algorithms for path optimization of autonomous mobile robot[J].Journal of Shanghai University:English Edition,2006,10(5):449-453.
[8] 陈 华,叶 东,陈 刚,等.遗传算法的数字图像相关搜索法[J].光学精密工程,2007,15(10):1633-1637.
[9] 曹 晖,周 延.多种群精英共享遗传算法在异常光谱识别中的应用[J].光谱学与光谱分析,2011,31(7):1847-1851.
[10]Fei Q,Li M,Wang B,et al.Analysis of cephalexin with NIR spectrometry coupled to artificial neural networks with modified genetic algorithm for wavelength selection[J].Chemometrics and Intelligent Laboratory Systems,2009,97:127-131.
[11]Thakur M.A new genetic algorithm for global optimization of multimodal continuous functions[J].Journal of Computational Science,2014,5:298-311.
[12]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010:6-9.

