财经类专业实践教学质量模糊综合评价

□文/张 丽

（大连财经学院 辽宁·大连）

一、“三维一体实践教学体系”的界定

“三维一体实践教学体系”，即以培养社会所需应用型财经类人才为立足点，以打造财经类专业核心竞争力为目标，全面、立体的从教学、科研、实验室建设三个维度出发，围绕课内实践、专项实践、综合实践的一体化构建实践教学体系。即教学、科研、实验室建设均以实践课程为中心展开建设。（图1）

二、财经类专业实践教学质量评价指标的选择

基于“三维一体实践教学体系”的财经类专业实践教学质量在建立评价指标体系时主要借鉴目前相对成熟的项目评价方法。首先，通过理论分析法对财经类专业实践课程的指导思想、具体内容、特征、主要影响进行比较分析，综合选择那些重要的影响条件和针对性强的指标；其次，采用频率统计法对目前有关教学质量评价研究的论文进行统计，选择高频指标；最后，在以上基础上，咨询相关专家意见，对指标体系进行调整。

评价标准必须与评价目标相一致，而上述指标体系的设立是以分解评价目标的方式来完成的。根据评价标准将评价等级分为：优、良、中、合格、不合格，即90 分以上为优，80～89 分为良，70～79 为中，60～69 为合格，60 分以下为不合格，用于对财经类专业实践教学质量单项指标及总体的评价。根据财经类专业的特点，本文设定了三个维度的指标，即教学维度指标、科研维度指标和实验室建设维度指标。

（一）教学维度指标的选择。教学活动分为教与学两个部分，虽然学生是教学活动的主体，但教师的自身素质对教学活动也存在重要的影响。教师的素质可以划分为主观因素和客观因素两个组成部分。主观因素是指教学态度，一个教师无论其能力有多大，如果教学态度不端正，就无法发挥其能力的全部。教学能力体现在诸多方面，本文认为教学内容、教学方法与手段是教学能力的主要表现形式。教学维度的最后一个指标是教学效果，值得注意的是，评价教学效果的时候，应该考虑学生的基础以及接受能力。

（二）科研维度指标。科研能力主要表现为论文和课题两个部分，其中论文是基础。科研课题的考核必须在保证课题质量的前提下考虑课题的数量。值得一提的是，许多评分体系中，科研经费的数量是一个重要指标。本文不同意这个观点，科研经费虽然在一定程度上可以反映科研课题的质量，但科研经费因专业而异，无法直接比较其研究水平。因此，本文建议在评价科研课题的时候，忽略科研经费因素。

（三）实验室建设维度指标。实验室建设分为三个阶段。首先，在校内应该建设高仿真实验室；其次，有条件的情况下，财经类专业应该设置校企联合课程。当然，最综合的应用能力培养活动应该是在实习基地完成的。拥有稳定的实习基础，对财经类专业的发展具有决定性的意义。

综上所述，本文的评价体系及评价标准见表1。（表1）依据表1，我们可以把财经类专业实践教学质量评价指标设定为：一级指标U=（U1，U2，U3）；二级指标Ui=（Ui1，Ui2，Ui3，Ui4，Ui5），其中i=（1，2，3）。建立中外合作办学高校教师教学质量的评语集并将其赋值。将各层各因素的评定等级分为优，良，中，合格，不合格五个等级。评语集V=（V1，V2，V3，V4，V5）=（优，良，中，合格，不合格）=（5，4，3，2，1）

三、财经类专业实践教学质量评价指标的处理

（一）财经类专业实践教学质量评价指标数值的同向化处理。一个指标体系的数值可能存在三个类型。第一种类型的指标，是数值越大，其水平越高，本文将这种指标称为正向指标；第二种类型的指标，是数值越小，其水平越高，本文将这种指标称为逆向指标；第三种类型的指标是越接近于某一个标准值，其水平越高，本文将这种指标称为摆动指标。三种类型的指标需要进行同向化处理。假设将三类指标都统一为正向指标，则综合评价的数值越大，结果就越理想。因为本文所涉及的全部指标数值都大于零，所以可以考虑将逆向指标取倒数，将其转化为正向指标。摆动指标的结果依赖于标准值的大小。可以考虑指标数值与标准值的距离，从而将其转化为逆向指标，再取倒数就可以转化为正向指标。

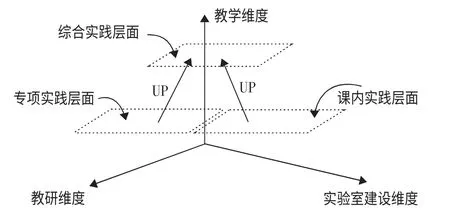
图1 三维一体教学体系

三类指标同向化公式总结如下：

（1）正向指标不需要处理。

（二）财经类专业实践教学质量评价指标数值的标准化处理。上文中，已经将指标数值进行了同向化处理，下面分析一下将正向指标标准化的方法。首先，既然取值范围要同一化，那么就必须放弃指标本来的意义。考虑到统计学中相关系数就是一个无量纲的数值，将取值范围统一为［0，1］这个区间（相关系数的取值范围是［-1，1］，但本文的指标数值都是正数，所以只有一半的区间）。具体的标准化思路是，可以将最大值定义为1，将最小值定义为0，其他数据以此为参考确定其数值。

指标的标准可以按照如下的步骤进行：（1）将指标数值排序；（2）确定最大值和最小值，分别定义为1 和0；（3）计算其他数值的对应数值，公式如下：

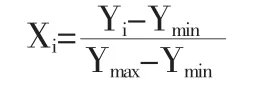
其中，Xi为标准化后的数值，Yi为同向化后尚未标准化的数值，Ymin为指标数值的最小值，Ymax为指标数值的最大值。

四、财经类专业实践教学质量各级评价指标权重的设置

确定一级、二级指标权重。一级评价指标因素U1，U2，U3，U4，U5 对应权重为b1h，b2h，b3h，b4h，b5h，其中bih （i=1，2，3，4，5）是第h 专家对该因素给定的一个权重值，且5i=1Σbih=1。本文采用模糊综合评价法来确定各级评价指标的权重。其具体步骤为：

（1）建立因素集：因素集是影响评价对象的各种因素所组成的集合，U=｛U1，U2，…，Un｝。

（2）建立评语集：评语就是对评价对象优劣程度的定性描述，V=｛v1，v2，…，vn｝。

（3）确定权重集：权重是描述各种指标相对于上级评价指标的相对重要程度。权重集是与评价因素相对应的多级集合，本文确定权重的方法AHP 法。AHP 法指系统工程中对非定量事件做定量分析的一种方法。其基本思想是由若干专家把处于同一子集中各指标相对于上级指标的重要性成对地进行比较，并把第i 个指标对第j 个指标的相对重要性的估计值记为ai，且，这样所有专家的评分构成了一组模糊判断矩阵，再综合这些专家的意见，使这样一组打分矩阵转化为一个综合判断矩阵，然后求得各指标的权重。这样一来，n 个指标成对比较的结果就可以用下面的判断矩阵A 表示为：

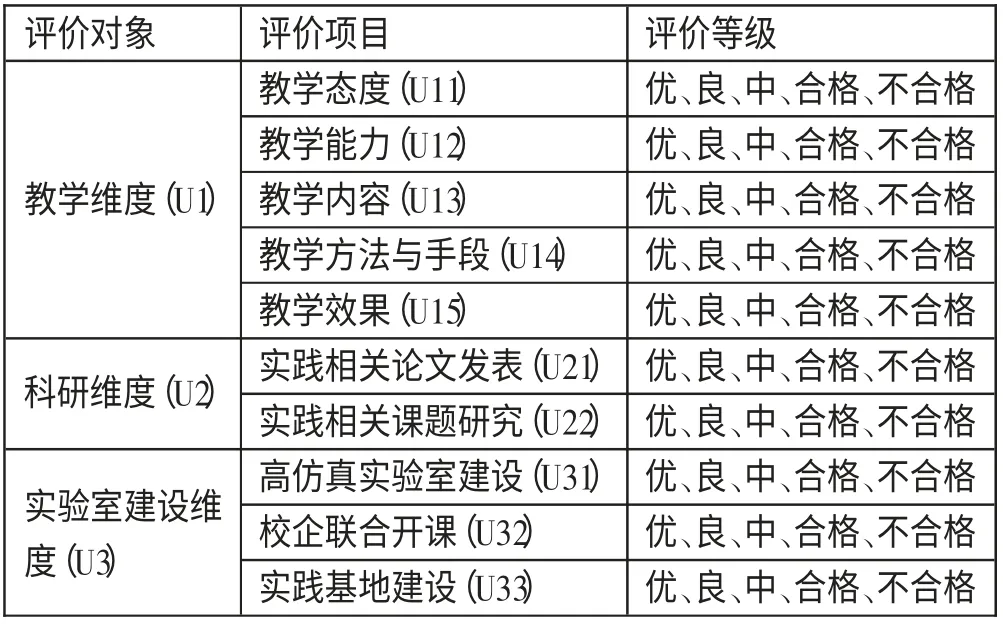
表1 财经类专业实践教学质量评价指标体系与评价标准

若矩阵A 为一致性矩阵，即矩阵A 中的元素满足aij=1/aji，aii=1，aij=aik·akj（i，j=1，…n），由矩阵理论可知道A 的最大特征根必为正实数，其对应特征向量的所有分量均同号，且最大特征根maxλ 对应的单位特征向量若为W=（w1，…，wn）则aij=wi/wj（i，j=1，2，…，n），i，j=1，2，…，n。从而W=（w1，…，wn）就是我们要获得的同一子集中的各指标相对于上级指标的权重向量，但实际操作时，由于矩阵A 中的各元素是通过同一指标集中的指标成对比较的结果，是通过主观估计获得的，因此并不一定是一致性矩阵。为了判断矩阵A 是否具有令人满意的一致性，需要引入随机一致性比率CR 进行检验：

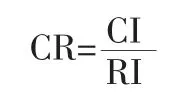
CI 称为判断矩阵的一般一致性矩阵；RI 称为判断矩阵的平均随机一致性指标；maxλ 为判断矩阵的最大特征值，n 为阶数，RI 为平均随机一致性指标，其取值如下：

当CR＜0.1 时，认为各指标相对上级指标具有较满意的一致性并接受该分析结果，否则要对各指标的权重系数重新修正，只有当所有的判断矩阵对应的检验指标通过了检验，这样计算出来的权重系数才是可信的。

五、财经类专业实践教学质量模糊综合评价

一般首先用统计调查法对指标体系中的各级评价指标隶属于各评语等级进行综合考察，考察结果用模糊评价（隶属度）矩阵Ri=（rijk）（i=1，2，…n；j=1，2，…li；k=1，2，…n）来表示，这里rijk 表示vij 对第k 个评语的隶属度。

具体评价采用的模糊算子法为：若A 和B 是n×m 和m×l的模糊矩阵，则它们的乘积C=A·B 为n×l 阵，其元素为：Cij=mk=1∨（aik∧bkj）（i=1，2，…，n；j=1，2，…i）。其中符号“∧”、“∨”的含义定为：a∧b=min（a，b），a∨b=max（a，b）。

具体过程由以下两个步骤完成：首先，计算第Ui（i=1，2，…，n）个指标的综合评价矩阵Bi（i=1，2，…，n），即Bi=Wi·Ri（i=1，2，…，n）。然后，对第一级指标作综合评价（即总的评价为U）。其中U 的评价矩阵为：B=（B1，B2，…，Bn）。权重向量为W1×n 作综合评价，得到U 的综合评价矩阵A=W·B。

［1］孙佩红，唐磊，李兴旺.多媒体教学质量模糊综合评价模型构建及实证分析［J］.内蒙古财经学院学报，2010.8.8.

［2］赵春元.基于层次分析法的教学质量模糊综合评价模型及应用［J］.沈阳工程学院学报，2011.4.