无线传感器网络中分阶段的无需测距定位算法*

马淑丽，赵建平

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

无线传感器网络中分阶段的无需测距定位算法*

马淑丽，赵建平

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

为了提高无线传感器网络中基于无需测距算法定位精度，改进质心算法和DV-Hop算法，定位过程分为两个阶段：第一阶段在最佳通信半径与最佳阈值下，用基于阈值的优先质心算法定位部分节点；第二阶段在最佳通信半径与最佳指数值下用DV-Hop算法定位剩余节点。将算法应用在一种锚节点人工部署环境下，并与其他算法对比。MTLAB仿真结果表明，改进的算法在不增加泛洪次数、计算量和网络硬件成本下能提高定位精度，同时实现100%定位。

无线传感器网络;质心算法;DV-Hop;最小均方差; 锚节点部署策略

0 引 言

无线传感器网络(Wireless Sensor Network,WSN)区域中分布着大量传感器节点[1-2]，节点将采集到的事件传递到用户，许多应用需要知道事件发生的位置[3-5]，所以节点定位技术相当重要[6]。现有的无线传感器网络定位算法大体分为高成本、高定位精度的基于测距算法(Range-based)和低成本、低定位精度的无需测距算法(Range-free)两类[7-10]。基于无需测距算法较为实用[8,11]，其中DV-Hop(Distance Vector-Hop[6])算法是应用最广泛的定位算法之一[3,12-13]。

DV-Hop算法定位精度受通信半径的影响[14]，不同通信半径对应不同的定位精度[11]。另外，还受网络拓扑结构影响[15]，DV-Hop算法在随机分布环境中由于平均跳距误差大[16]、跳段距离代替直线距离[12]等定位精度较低[11,14]。为解决这些问题，提高定位精度，许多文献优化通信半径,减小平均跳距误差或优化锚节点分布方案等。如文献[14]提出一种基于最优通信半径改进的DV-Hop算法，并采用一种锚节点分布策略进一步提升定位精度。文献[11]提出锚节点双通信半径定位算法。文献[16-18]修正锚节点平均每跳距离，定位节点加权处理平均每跳距离。文献[15,19]用最小均方差准则求平均每跳距离。在一些应用中，锚节点可以固定在区域中某位置[20-21]。文献[2,22]指出锚节点的均匀部署能提高定位精度。文献[19]将其改进的算法应用在锚节点人工均匀部署的环境中。文献[23]提出最小均方差准则下的最佳指数值求平均每跳距离，并将其应用在一种锚节点人工部署的环境中。文献[24]提出一种锚节点人工部署方案，并改进DV-Hop算法，提高了定位精度，同时具有较强的稳定性[11]。文献[25]指出未知节点周围的锚节点能构成等边三角形顶点时定位误差最小。文献[26]提出锚节点部署在小区域的几何中心时可大大提高DV-Hop算法定位精度。优化的锚节点部署方式可以大大提高定位性能[14]，缺点是增加了人工负担，对有些应用难以实现[11]。

文献[27]先选择合适的锚节点进行初始定位，然后用迭代算法优化节点位置，精确定位的节点升级锚节点，参与下一阶段定位。文献[28]指出所有锚节点参与定位时误差不是最小，参与定位的锚节点与未知节点位置越近定位精度越高，并设定阈值限制参与定位的锚节点个数。本文结合上述文献，改进基于无需测距的定位算法，在一种锚节点人工部署的环境中，提出分两个阶段定位：第一阶段用基于阈值的优先质心定位算法，用阈值限制参与定位的锚节点个数，找出最佳阈值下最佳通信半径，优先定位部分节点；第二阶段在最佳通信半径下，求出最佳指数值，用最佳指数值下的DV-HOP算法定位剩余节点，最终实现100%定位。

1 算法概述

1.1 质心算法

质心算法(Centroid)，是一种基于无需测距的定位算法[2,13]，由南加利福尼亚大学Nirupama Bulusu等人提出[29]。节点坐标定位在其一跳范围内锚节点的几何中心[30]，如下式：

(1)

式中，(x,y)是未知节点坐标，(xi,yi)是定位节点周围一跳距离锚节点i的坐标，n是定位节点周围一跳距离锚节点的个数。

在无线传感器网络区域中，未知节点一般随机分布。由于未知节点可能在区域的任何位置，质心算法定位误差会很大[31-32]。本文将区域划分为较小的区域，在较小的交叉区域[33]内实现质心定位。

1.2 DV-Hop算法

DV-Hop定位算法是由美国罗格斯大学(Rutgers University)Dragos Niculescu提出的6种分布式定位算法之一[3，22]。

定位过程[2，8，13]分为4阶段：

Step1 锚节点以泛洪方式向网络传播自身位置信息和初始跳数值0。接收节点将锚节点位置信息和跳数值保留下来，并将跳数值加1转发出去。在多次转发过程中，接收节点保留锚节点的位置信息和最小跳数值。当接收到的跳数值小于自己保留的跳数值，则更新跳数值。当接收到的跳数值大于自己保留的跳数值，则抛弃接收到的跳数值。最后，网络中每个节点知道所有锚节点的位置信息和与所有锚节点的最小跳数值。

Step2 锚节点根据到其他锚节点的实际位置信息和跳数值，计算自己的平均每跳距离。

有两种方法[15]：一种方法是，根据无偏估计准则计算平均每跳距离：

(2)

另一种方法是基于最小均方误差准则计算平均每跳距离：

(3)

式中，dHopi是锚节点i到其他锚节点的平均每一跳距离。hij是锚节点i，j间的最小跳数。xi，yi是锚节点i坐标值，xj，yj是锚节点j坐标值。dij是锚节点i、j间的距离。大多数文献使用第一种方法，文献[15]指出第二种方法更合理。本文采用第二种方法。

Step3 锚节点将平均每跳距离作为校正值以泛洪方式广播出去。网络中所有未知节点只接收第一个到达的校正值，即只保留离自己最近的锚节点校正值。然后，未知节点计算自己与每个锚节点的估计距离，如式(4)所示：

dmk=dHopm×hmk

(4)

式中，dmk为未知节点m到锚节点k的估计距离，dHopm为未知节点m的校正值，hmk为未知节点m到锚节点k的最小跳数值。

Step4 当未知节点得到与3个以上锚节点[2]的估计距离后，代入式(5)，用多边测量法定位[4]。最终得到未知节点的估算坐标。

(5)

AX=b

(6)

(7)

(8)

(9)

式中，di是未知节点与锚节点i间的估算距离，x，y是未知节点估计坐标值，xi，yi是锚节点i坐标值，n是锚节点个数。X为未知节点的估算坐标阵。

1.3 锚节点人工部署策略

不同的应用环境对应不同的节点部署策略，如文献[4]应用在河流监测环境中，节点分布呈带状。许多应用(如农业监测、环境检测等)在二维环境中, 锚节点位置固定已知或有GPS等设备能自定位，未知节点随机分布(如飞机撒落[6])。文献[34]指出基于无需测距的DV-Hop定位算法的定位精度受限于网络中节点分布的均匀性。文献[35]研究了圆形区域内节点分布均匀性对定位精度的影响，并在其提出的圆形均匀分布环境中用3种无需测距的算法仿真。

文献[24]提出了一种均匀二维锚节点分布方式：利用欧式范数，根据式(9)推导出相对定位误差最小时，其锚节点分布满足下式：

(10)

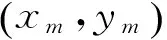
文献[26]提出的环境：将正方形区域划分为大小相同的小正方形，每个小正方形内切圆中心放置1个锚节点，其他未知节点随机分布，并将其提出的锚节点部署策略与其他文献对比，证明有一定优势

2 应用环境与改进定位算法

2.1 应用环境

经研究，文献[26]提出的部署方式更能提高DV-Hop算法的定位精度。本文考虑将质心定位算法应用在其环境中。并研究质心算法在文献[26]环境下的定位规律。

2.2 第一阶段：基于最佳阈值的优先质心算法

当未知节点的优先值大于阈值(yu)时，该未知节点可参与第一阶段定位，否则参与第二阶段定位。优先值，指未知节点在其通信范围内即一跳锚节点的个数。参与第一阶段定位的未知节点，将其满足阈值的周围锚节点坐标信息，代入式(1)求自身坐标值。

若网络中锚节点个数为n，则阈值可设为0～n之间的任何整数。经研究，不同的阈值和不同通信半径对应不同的定位精度。本文在实际应用前，先根据实际环境建立仿真，求出最佳阈值和最佳通信半径。将仿真出的最佳阈值和最佳通信半径用到本文算法第一阶段，求出部分节点的坐标。

2.3 第二阶段：最佳指数下DV-Hop

基于最小均方误差准则计算平均每跳距离如式(3)所示。文献[23]改进式(3)中分母hij的指数，精化锚节点i的平均每一跳距离dHopi，如式(11)。提出在不同锚节点覆盖率和不同通信半径下取1.9到2.0范围内最佳指数值时，能提高DV-Hop算法定位精度。

(11)

首先根据剩余节点仿真DV-Hop算法，找出最佳阈值和最佳通信半径下对应的最佳指数值α。第二阶段将最佳指数值α带入式(11)求平均每跳距离，并用DV-Hop定位剩余节点。经研究发现在一定的节点个数与通信半径下，α的取值范围可扩大到1.7～2.0，使DV-Hop算法用式(11)求平均每跳距离比用式(2)、式(3)求平均每跳距离定位精度要高。

2.4 将上述3种方法结合

本文算法定位步骤：

首先，准备工作——仿真应用环境，计算最佳值工作。仿真第一、第二阶段求最佳阈值，最佳通信半径、最佳指数值。

然后，实际定位。选取最佳通信半径的节点，按照文献[26]节点部署方式将节点分布在网络区域。第一阶段：1.锚节点以泛洪方式向网络发送自身位置信息和初始跳数值。接收节点保留信息，并将跳数值加1后转发。多次转发过程中，接收节点只更新比自己先前保留的较小的跳数值，当接收到比自己先前保留的跳数值大的则不更新。最终，每个节点存有与所有锚节点间的最小跳数值和所有锚节点的坐标值。2.用基于阈值的优先质心算法先定位部分节点，阈值取最佳值。未知节点根据保留的与锚节点的最小跳数值，计算优先值(即求一跳的锚节点个数)，然后判断优先值是否大于阈值，若大于阈值，则未知节点进行自定位，将保留的一跳距离的锚节点位置信息代入式(1)计算出自身坐标。若小于阈值，则参与第二阶段定位。第二阶段：锚节点根据收到的其他锚节点位置信息和跳数值，用式(11)求出自己的平均每一跳距离(α取最佳指数值)，并作为校正值以泛洪方式广播至网络。剩余未定位的节点，只保留第一个送达的校正值，然后将与各锚节点间的最小跳数值，代入式(4)求出自身与各锚节点间的估计距离，当求出超过3个锚节点估计距离时，用多边测量法定位。最终实现节点100%定位。

3 仿真结果分析

无需测距算法广泛应用在粗精度定位的应用中，达到0.4以下即可满足应用[27，36，37]。本文算法考虑降低网络成本、减小节点能耗等问题，控制定位精度在0.4以下、锚节点覆盖率4%～16%以内，通信半径13～49 m以内，网络连通度6～75以内。由于节点分布随机性，程序仿真100次。

3.1 应用环境验证

按文献[26]提出的锚节点部署方式， 锚节点覆盖率分别取4%、9%、16%、25%、36%、49%。监控区域边长100 m，网络节点总数100个,未知节点随机分布。将质心算法、DV-Hop算法在两种锚节点部署方式下进行对比。

如图1所示，锚节点均匀部署下的质心算法比锚节点随机部署下的质心算法和DV-Hop算法定位精度高。在锚节点均匀部署的环境下，质心定位算法比DV-Hop算法占优势。说明文献[26]锚节点部署方式更适于质心定位算法。

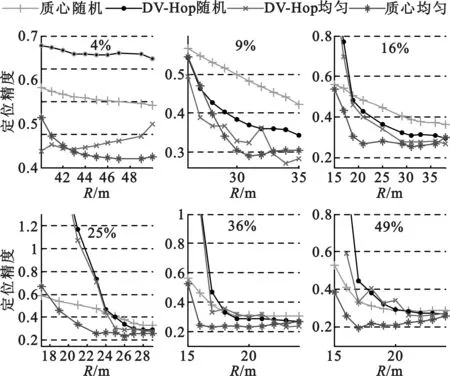
图1 质心算法和DV-HOP算法在两种环境下对比

定位精度(Accuracy)指网络中全部节点(N个)的平均定位误差与节点通信半径R的比值，值越小说明定位精度越高，计算如式(12)所示:

(12)

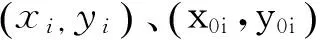
3.2 仿真第一阶段

在不同的通信半径、不同的阈值、不同的锚节点覆盖率下仿真本文算法第一阶段，求出锚节点覆盖率分别为4%、9%、16%时，较优的阈值范围和较优的通信半径范围。

3.2.1 锚节点覆盖率4%

当锚节点覆盖率4%时，仿真基于阈值的优先质心定位算法和DV-Hop定位算法。为确保第一阶段定位节点数大于0，且第一阶段算法比DV-Hop算法定位精度更占优势，多次试验，得出本文第一阶段仿真的较优的阈值范围和较优的通信半径范围为图2中对应的范围，其中不同的阈值对应不同的较优通信半径范围。

如图2(a)所示，在一定通信半径范围内，基于阈值的优先质心算法比DV-Hop算法定位精度要高。阈值为3时，基于阈值的优先质心算法定位精度与DV-Hop曲线重合。

在不同的阈值和不同的通信半径下基于阈值的优先质心算法定位节点数不同，如图2(b)所示，阈值越大定位节点数越少。

(a)DV-HOP算法和基于阈值的优先质心算法

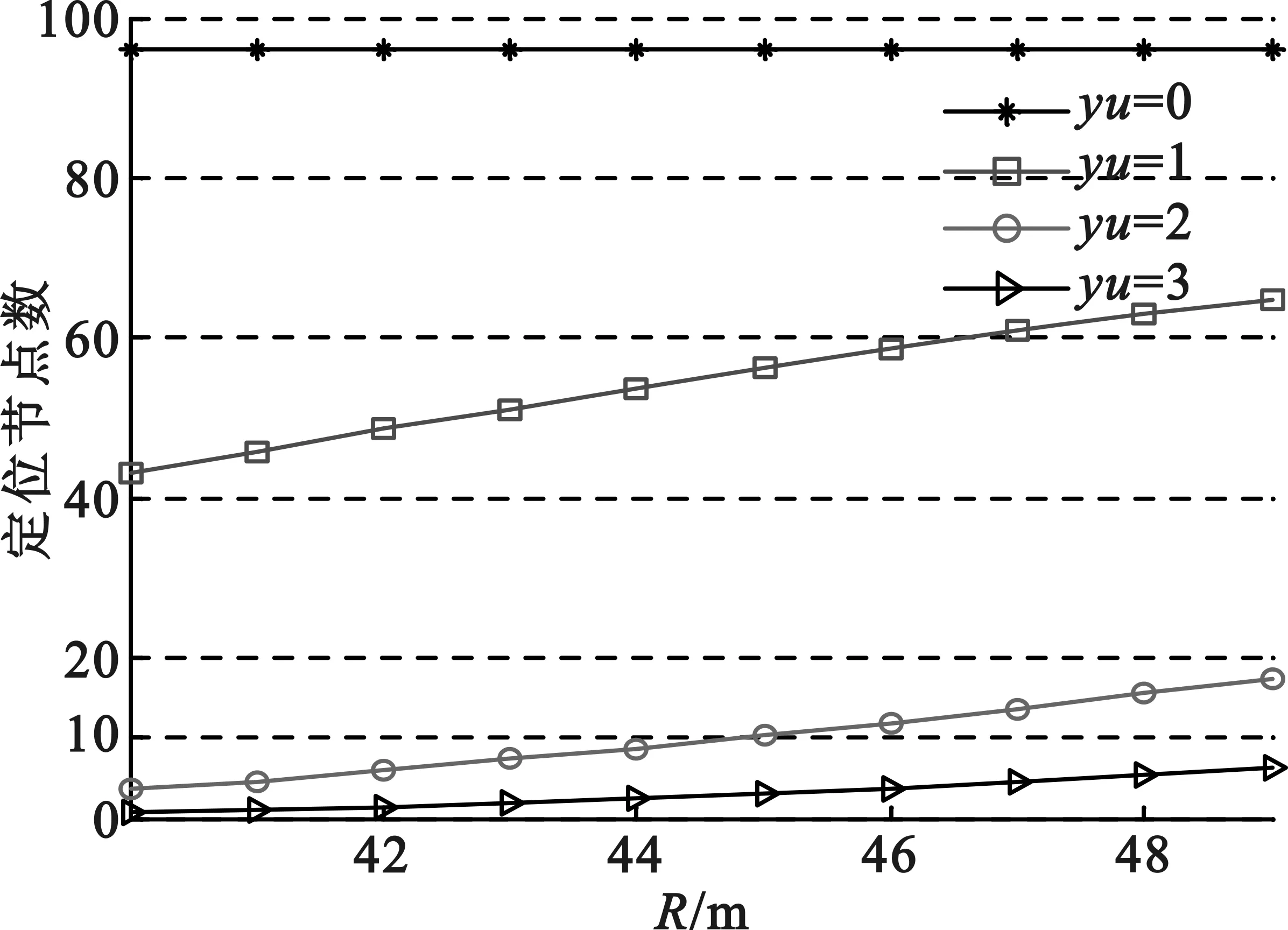
(b)基于阈值的优先质心定位节点数

3.2.2 锚节点覆盖率9%

同理，当锚节点覆盖率9%时，阈值取0～5，通信半径范围26～49 m，较优的阈值范围和较优的通信半径范围为图3中对应的范围，不同的阈值对应不同的较优通信半径范围，且阈值越大定位节点数越少。

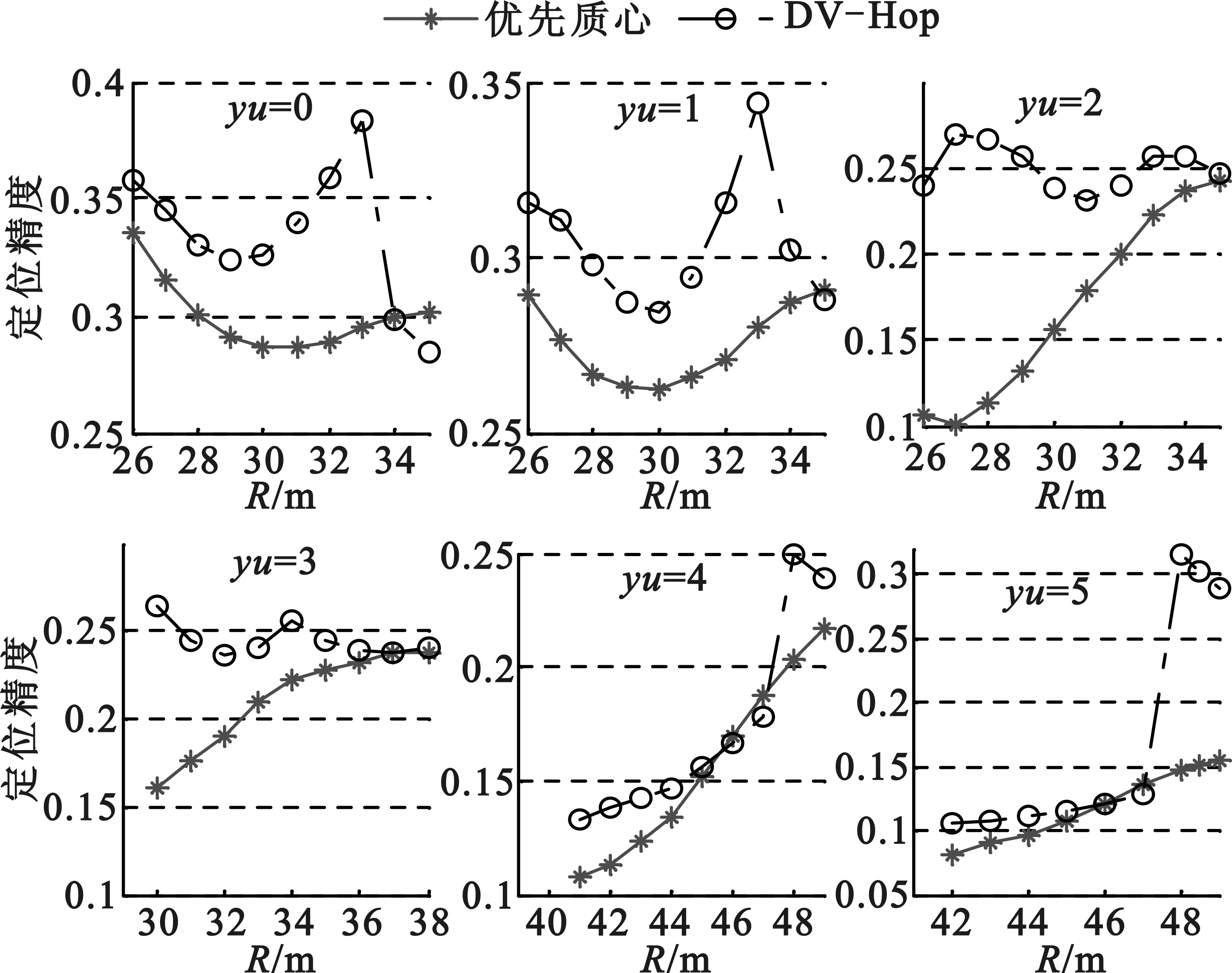
(a)基于阈值的优先质心算法和DV-HOP算法

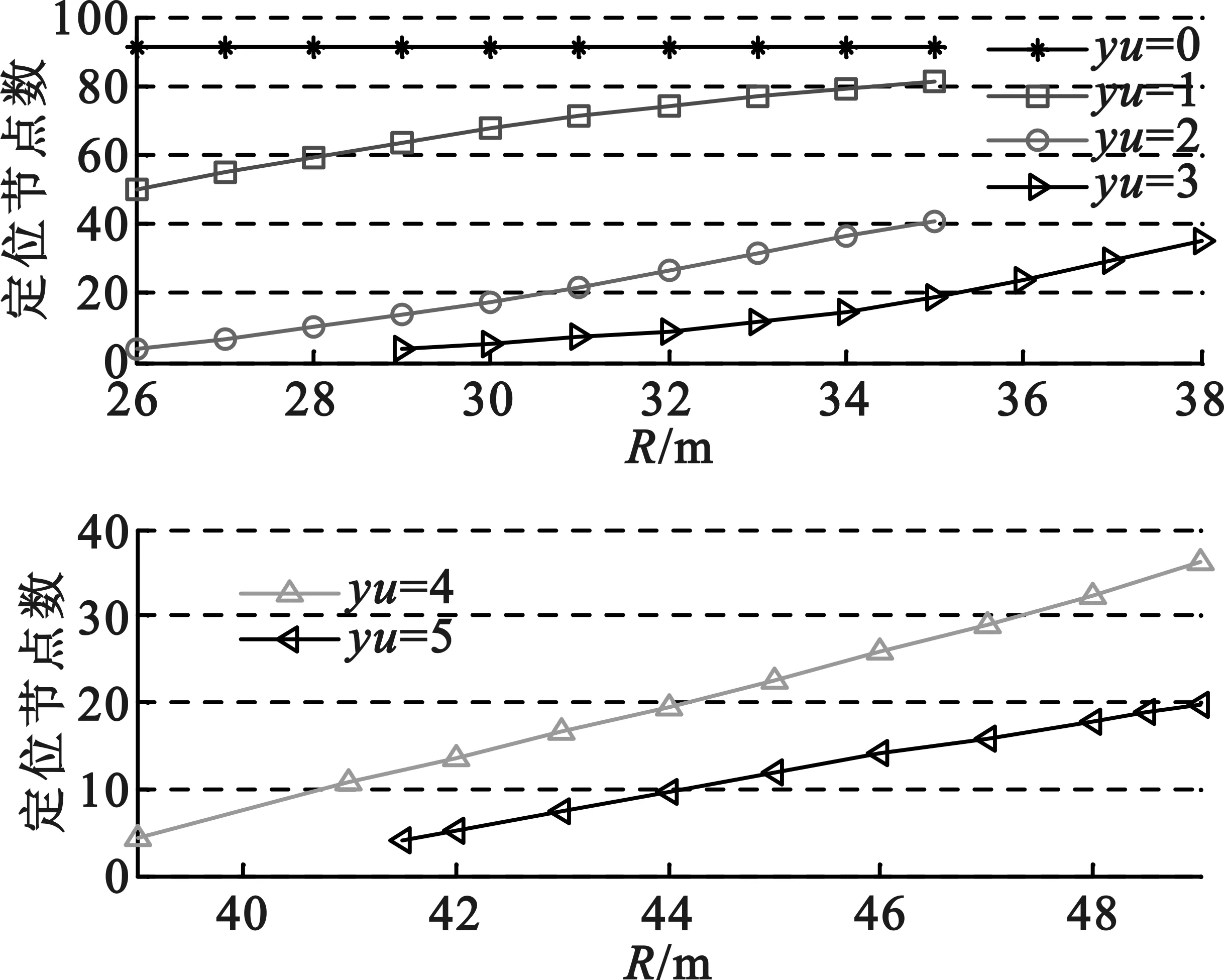
(b)基于阈值的优先质心定位节点数

3.2.3 锚节点覆盖率16%

锚节点覆盖率16%时,阈值取0～9，通信半径范围13～49 m，基于阈值的优先质心定位算法定位精度占优势，且阈值越大定位节点数越少，如图4所示。

(a)基于阈值的优先质心算法和DV-HOP算法yu=0～3

(b)基于阈值的优先质心算法和DV-HOP算法yu=4～9

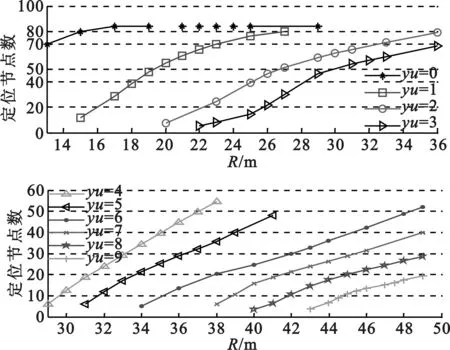
(c)基于阈值的优先质心定位节点数

3.3 仿真第二阶段

将第一阶段用基于阈值的优先质心算法，第二阶段用式(2)求锚节点平均跳距的DV-Hop算法用Range-free(A)表示。将第一阶段用基于阈值的优先质心算法，第二阶段用式(11)求锚节点平均跳距的DV-Hop算法(α范围取1.7～2.1)用Range-free(B)表示。在锚节点覆盖率4%、9%、16%下，分别仿真较优阈值、较优通信半径范围内的两种算法，找出最佳阈值、最佳通信半径和最佳指数。

3.3.1 锚节点覆盖率4%

如图5所示，锚节点覆盖率4%，阈值yu为1时，Range-free(B)算法定位精度最高为0.33，比Range-free(A)算法定位精度提升3%，此时通信半径R为44 m，指数值eq为1.83。阈值yu为2时，定位精度最高为0.319，比Range-free(A)算法定位精度提升6%，此时通信半径R为46m，指数值eq为1.78。得出，锚节点覆盖率为4%时，最佳阈值为2，最佳通信半径为46m，最佳指数值为1. 78。

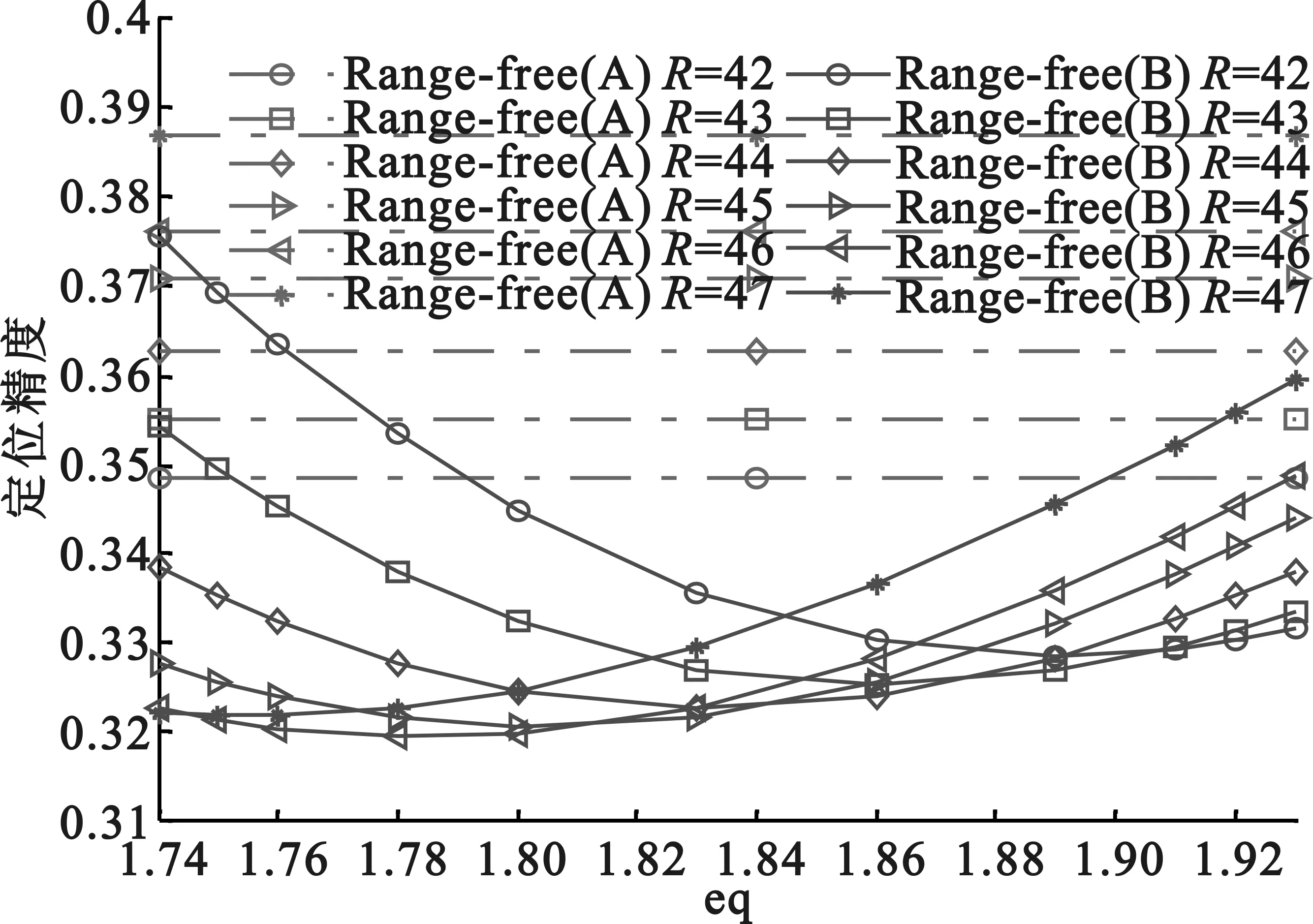
(b)yu=2

3.3.2 锚节点覆盖率9%、16%

同理，锚节点覆盖率为9%时，Range-free(B)算法最佳阈值为5，最高定位精度0.25，比Range-free(A)算法定位精度提升0.17%，最佳通信半径49 m，最佳指数值1.935，如图6(a)所示。锚节点覆盖率为16%时，最佳阈值为5，最高定位精度0.2193，比Range-free(A)算法定位精度提升3.42%，最佳通信半径35 m，最佳指数值1.93，如图6(b)所示。

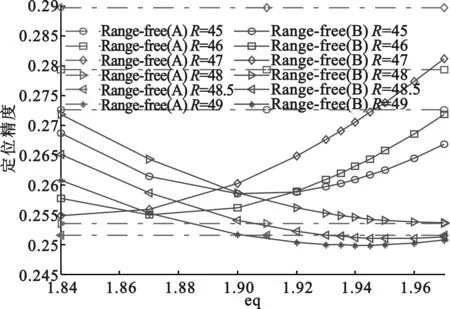
(a)n=9% yu=5

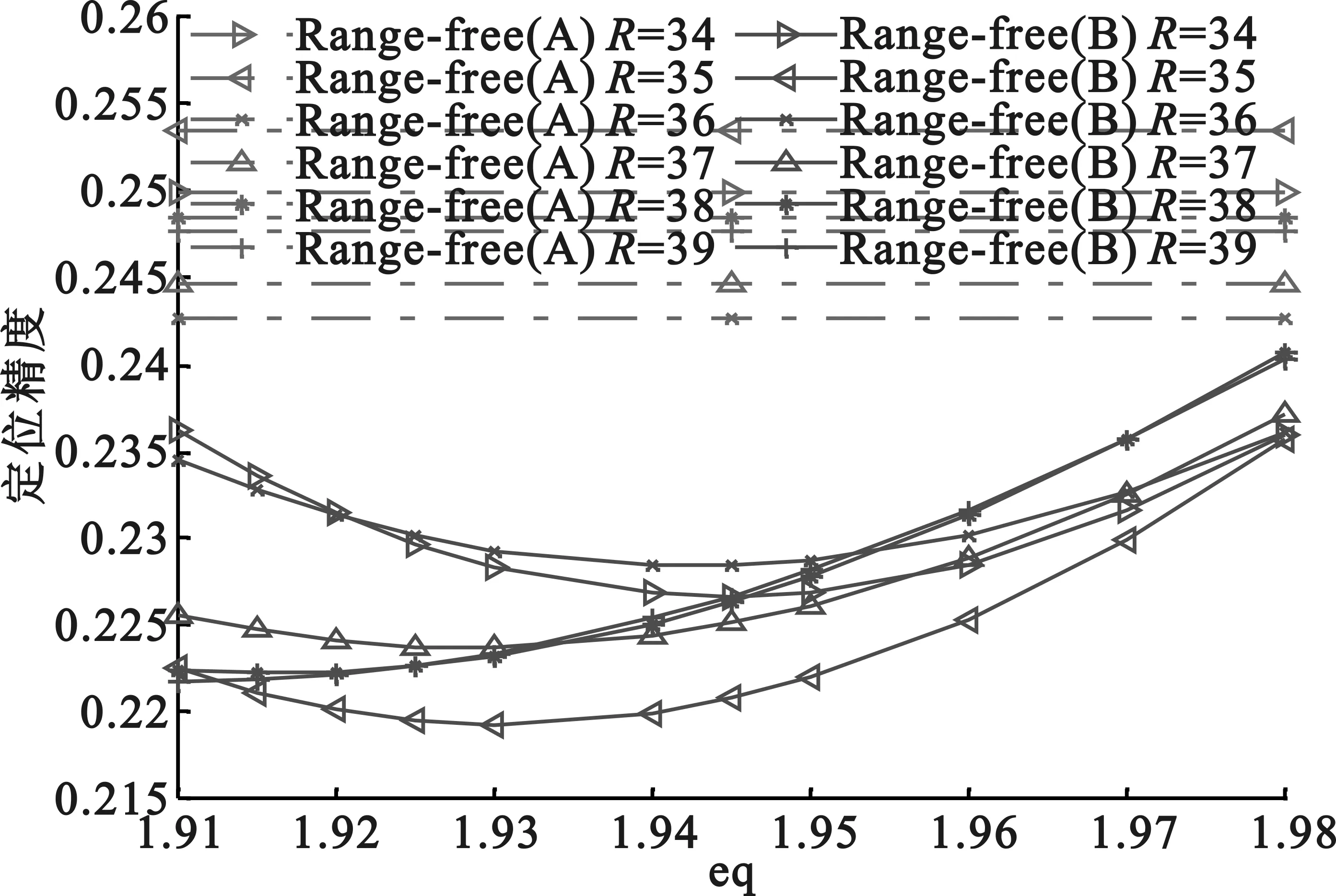
(b)n=16% yu=5

3.4 本文算法

如表1所示，本文算法在3种锚节点覆盖率下最高定位精度(AC)分别比DV-Hop算法定位精度(AC)提升36%、9.3%、8.5%。

表1 本文算法最高定位精度与DV-Hop算法定位精度

在相同的节点个数、通信半径、网络连通度、锚节点覆盖率下，将本文算法Range-free(B)与其它算法对比。锚节点随机部署下的DV-Hop算法用Range-free(S)表示，锚节点随机部署下最佳指数值的DV-Hop算法用Range-free(SE)表示，锚节点均匀部署的DV-Hop用Range-free(J)表示，锚节点均匀部署下最佳指数值的DV-Hop算法用Range-free(JE)表示。锚节点覆盖率4%、9%时，本文算法取最佳阈值，在一定的通信半径范围内，取对应的最佳指数值，如图7(a)、图7 (b)所示，定位精度比其它算法高。锚节点覆盖率为16%时，在较优的阈值范围内，取对应的最佳通信半径和最佳指数值，如图7(c)所示，本文算法定位精度也比其它算法高。

(a)4% yu=2

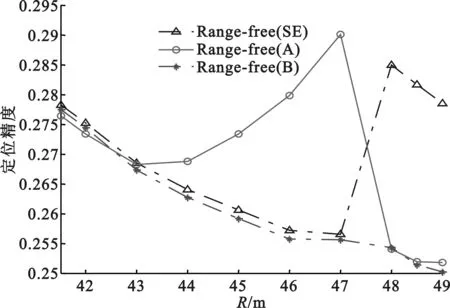
(b)9% yu=5

(c)16%

4 结 语

首先验证了质心算法适于一种锚节点人工部署环境，然后提出了改进的基于无需测距的算法，将定位分为两个阶段，第一阶段改进质心算法定位部分节点，第二阶段改进DV-Hop算法定位剩余节点。锚节点个数为4时，本文算法比DV-Hop算法提高定位精度36%，使基于无需测距的定位算法在较低的锚节点个数下，能应用到一般的粗精度定位中。锚节点覆盖率9%、16%时定位精度比DV-Hop算法分别提升9.3%、8.5%。优点是在不增加网络硬件成本、泛洪次数和计算量下能提高定位精度，实现100%定位，缺点是采用人工部署锚节点的方式增加了人力负担。下一步将研究基于多通信半径的无需测距定位算法，进一步提升定位精度。

[1] LIU Jin-long, WU Zhi-lu, YIN Zhen-dong.An Improved Location Algorithm in Wireless Sensor Network[C]. Optoelectronics and Microelectronics (ICOM), 2013 International Conference on. IEEE(Sept2013)255-258.

[2] Gayan S; Dias D. Improved Dv-hop Algorithm Through Anchor Position Re-Estimation[C]. Wireless and Mobile, 2014 IEEE Asia Pacific Conference on. (Aug 2014)126-131.

[3] WANG, CHEN, An Improved DV-Distance Localization Algorithm for Wireless Sensor Networks[C]. Advanced Computer Control (ICACC), 2010 2nd International Conference on .IEEE, March 2010 , Volume 5 ,472-476.

[4] HOU Shou-feng, ZHOU Xiao-jia, LIU Xin-xin. A Novel DV-Hop Localization Algorithm for Asymmetry Distributed Wireless Sensor Networks[C].Computer Science and Information Technology (ICCSIT) Conference (Volume:4 ), IEEE(July 2010)243-248.

[5] Hadir A, Zine-Dine K, Bakhouya M, El Kafi J. An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks[C]. Next Generation Networks and Services (NGNS), 2014 Fifth International Conference on. IEEE(May2014)330-334.

[6] DAI Ying, WANG Jian-ping, ZHANG Chong-wei. Improvement of DV-Hop Localization Algorithms for Wireless Sensor Networks[C].Wireless Communications Networking and Mobile Computing(WiCOM),2010 6th International Conference on.IEEE,Sept2010,1-4.

[7] Kirci P, Chaouchi H, Laouiti A. Wireless Sensor Networks and Efficient Localisation[C]. Future Internet of Things and Cloud (FiCloud), 2014 International Conference on. IEEE, Aug 2014, 98-100.

[8] CHANG Xiao-hui, LUO Xiong. An Improved Self-Localization Algorithm for Ad Hoc Network based on Extreme Learning Machine[C].Intelligent Control and Automation (WCICA),2014 11th World Congress on.IEEE,2014,564-569.

[9] ZHANG Shu-zhen, LI Shan-cang. A Distributed Self-Localization Algorithm for Wireless Sensor Networks[C].Computer Engineering and Technology (ICCET), 2010 2nd International Conference on. IEEE, April 2010, Volume 6,197-200.

[10] 李彬,王文杰,殷勤业等.一种利用天线旋转的无线传感器网络定位算法[J].西安交通大学学报,2011, 45(04):60-66. LI Bin, WANG Wen-jie, YIN Qin-ye. A Localization Method Using Rotary Antennas in Wireless Sensor Networks[J].Journal of Xi′an Jiaotong University, 2011,45(04)：60-66.

[11] 李娟,刘禹,钱志鸿.基于双通信半径的传感器网DV-Hop定位算法[J].吉林大学学报:工学版，2014,44(02)：502-507. LI Juan, LIU Yu, QIAN Zhi-hong. Improved DV-Hop Localization Algorithm based on Two Communication Ranges for Wireless Sensor Network[J]. Journal of Jilin University (Engineering and Technology Edition),2014,44(02):502-507.

[12] LI Chang-yu, ZHAO Pei-zhe, YU Zeng. Improved DV-Hop Localization Algorithm for Wireless Nodes in the Smart Grid[C]. Control and Decision Conference (2014 CCDC), the 26th Chinese，IEEE, 2014, 4535-4540.

[13] HU Juan, JIANG Min-lan. An Improved Node Localization Algorithm in Wireless Sensor Network[C]. Advanced Research and Technology in Industry Applications (WARTIA), 2014 IEEE Workshop on, Sept 2014, 398-401.

[14] 吴玉成,李江雯.基于最优节点通信半径的改进DV-Hop定位算法[J].华南理工大学学报:自然科学版,2012, 40(06):37-42. WU Yu-cheng,LI Jiang-wen.Improved DV-Hop Localization Algorithm based on Optimal Communication Radius of Nodes [J].Journal of South China University of Technology(Natural Science Edition),2012,40 (06):37-42.

[15] 嵇玮玮,刘中.定位算法在随机传感器网络中的应用研究[J].电子与信息学报，2008,30(04)：970-974. JI Wei-wei, LIU Zhong. Study on the Application of DY-Hop Localization Algorithms to Random Sensor Networks[J]. Journal of Electronics & Information Technology，2008,30(04)：970-974.

[16] YUAN Bing, YU Zhen, LU Hong-fei, SHU Bing. The Optimization Research of Node Localization Algorithm based on Wireless Sensor Network[C].Biomedical Engineering and Informatics (BMEI), 2014 7th International Conference on.IEEE,Oct.2014,929-934.

[17] BAO Xi-rong, BAO Fu-peng, ZHANG Shi, LIU Lei. An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks[C]. Wireless Communications Networking and Mobile Computing (WiCOM),2010 6th International Conference on. IEEE,Sept2010, 1-4.

[18] 林金朝,陈晓冰,刘海波.基于平均跳距修正的无线传感器网络节点迭代定位算法[J].通信学报，2009,30(10)：107-113. LIN Jin-zhao, CHEN Xiao-bing, LIU Hai-bo. Iterative Algorithm for Locating Nodes in WSN based on Modifying Average Hopping Distances[J]. Journal on Communications, 2009,30(10)：107-113.

[19] 魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法[J].西安交通大学学报,2014,48(06):1-6. WEI Quan-rui, LIU Jun, HAN Jiu-qiang. An Improved DV-hop Node Localization Algorithm based on Unbiased Estimation for Wireless Sensor Networks[J]. Journal of Xi′an Jiaotong University,2014,48(06):1-6.

[20] Gayan S,Dias D. Novel Enhancements for Node Localization in Wireless Sensor Networks[C]. Information and Automation for Sustainability (ICIAfS),2014 7th International Conference on.IEEE, Dec2014,1-7.

[21] Hadir A,Zine-Dine K,Bakhouya M,El Kafi J. An Optimized DV-Hop Localization Algorithm Using Average Hop Weighted Mean in WSNs [C].Codes, Cryptography and Communication Systems (WCCCS), 2014 5th Workshop on. IEEE,Nov2014,25-29.

[22] FANG Wang-sheng,YANG Guang-yu.Improvement based on DV-Hop Localization Algorithm of Wireless Sensor Network[C].Mechatronic Science, Electric Engineering and Computer(MEC),2011 International Conference on.IEEE,Aug 2011,2421-2424.

[23] 马淑丽,赵建平.无线传感器网络中DV-Hop定位算法的改进[J].通信技术,2015,48(07):840-844. MA Shu-li,ZHAO Jian-ping.The Improvement of DV-Hop Algorithm in Wirless Sensor Networks[J]. Communications Technology, 2015, 48(07):840-844.

[24] ZHENG You-si, WAN Lei,SUN Zhi,et al.A Long Range DV-Hop Localization Algorithm with Placement Strategy in Wireless Sensor Networks[C].Wireless Communications, Networking and Mobile Computing, 2008. WiCOM ′08. 4th International Conference on.IEEE,Oct 2008,1-5.

[25] 刘瑾.无线传感器网络定位算法的研究及应用[D].南京:南京航空航天大学:25-27. LIN Jin. Research and Application of Wireless Sensor Network Localization Algorithm[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 25-27.

[26] 马淑丽,赵建平,张炳婷等.WSN中节点定位方法的改进[J].通信技术,2015,48(04):453-457. MA Shu-li,ZHAO Jian-ping,ZHANG Bing-ting,et al.Improvement of Node Locating Algorithm in WSN[J].Communications Technology,2015,48(04):453-457.

[27] 王翥,郝晓强,王玲.基于锚节点选择的无线传感器网络定位算法[J].计算机研究与应用，2010,47(S)：31-34. WANG Zhu,HAO Xiao-qiang,WANG Ling.Choice of Location-based Anchor Node Localization Algorithm for Wireless Sensor Networks[J]. Journal of Computer Research and Development,2010, 47(S)：31-34.

[28] 申铉京,李成岳,王硕.基于最优锚节点的无线传感器网络节点定位算法[J].吉林大学学报:工学版,2011,41 (S1):208-214. SHEN Xuan-jing,LI Cheng-yue,WANG Shuo.Localization Algorithm based on Optimal Nodes for Wireless Sensor Networks[J]. Journal of Jilin University (Engineering and Technology Edition),2011,41(S1):208-214.

[29] (德)达尔吉,(美)玻尔拉伯尔.无线传感器网络基础理与实践[M].孙利民等译.北京：清华大学出版社，2014. (Germany) Dargie W,(America) Poellabaure C. The Wireless Sensor Network Basic Theory and Practice [M]. SUN M L Translation. Qinghua University Press, 2014.

[30] 杨新宇,孔庆茹,戴湘军.一种改进的加权质心定位算法[J].西安交通大学学报,2010,44(08):1-4. YANG Xin-yu,KONG Qing-ru,DAI Xiang-jun.An Improved Weighted Centroid Location Algorithm[J].Journal of Xi′an Jiaotong University,2010,44(08):1-4.

[31] XIE Shao-guo,HU Yan-jun,WANG Yi. Weighted Centroid Localization for Wireless Sensor Networks[C]. Consumer Electronics-China,2014 IEEE International Conference on.April 2014,1-4.

[32] 闫斌,周小佳,王厚军等.无线传感器网络功率控制的质心定位算法[J].电子科技大学学报，2010,39(03)：416-419. YAN Bin,ZHOU Xiao-jia,WANG Hou-jun,et al.Centroid Localization Algorithm based on Power Control in Wireless Sensor Networks[J]. Journal of University of Electronic Science and Technology of China，2010,39(03)：416-419.

[33] CHEN Liang-yin,LI Miao,LIU Kai.Distributed Range-Free Localisation Algorithm for Wireless Sensor Networks[J].Electronics Letters, IET Journals & Magazines,2014, 50(12): 894-896.

[34] 李新春,王晓明.节点分布对无线传感器节点定位性能的影响[J].计算机工程与应用.http://www.cnki. net/kcms/detail/11.2127.TP.20150116.1123.017.html, 2015-1-16. LI Xin-chun,WANG Xiao-ming. Node Distribution Effect on the Performance of Wireless Sensor Node Localization [J]. Computer Engineering and Applications.http: //www.cnki. net /kcms/ detail / 11.2127.TP. 2015 0116.1123.017.html, 2015-1-16.

[35] 宫娜娜,武海艳.传感器网络节点分布均匀性与定位性能的关系[J].电子测量技术，2014，37(12):80-85. GONG Na-na,WU Hai-yan. The Relationship Between the Sensor Network Node Distribution Uniformity and Positioning Performance[J].Electronic Measurement Technology, 2014,37(12):80-85.

[36] 江禹生,冯砚毫,管芳等.无线传感网非测距三维节点定位算法[J].西安电子科技大学学报:自然科学版,2012,39(05):140-147. JIANG Yu-sheng,FENG Yan-hao,GUAN Fang,et al.Range-Free Three-Dimensional Node Location Algorithm for the Wireless Sensor Network[J].Journal of Xidian University,2012,39(05):140-147.

[37] 周正.无线传感器网络的节点自定位技术[J].中兴通信技术，2005,11(04):51-56. ZHOU Zheng.Self-Localization Technologies for Wireless Sensor Network Nodes[J].ZTE Communications,2005,11(04):51-56.

A Range-Free Localization Algorithm in Stages for Wireless Sensor Network

MA Shu-li，ZHAO Jian-ping

(College of Physics Engineering ，Qufu Normal University ， Qufu Shandon 273165，China )

In order to optimize the rang-free algorithm in wireless sensor network, the centroid algorithm and DV-Hop algorithm are improved, and the positioning process is divided into two stages: the first stage, under the optimal communication radius and optimal threshold, with threshold-based priority centroid localization algorithm for locating parts of nodes; the second stage, in the best communication radius and the best index value with DV hop positioning algorithm for locating the remaining nodes. The algorithm is applied to an anchor node artificial deployment environment and compared with other algorithms. MTLAB simulation results show that the improved algorithm can enhance the positioning accuracy without any increase of flooding times, and achieve 100% positioning, without any increase of network-hardware cost.

wireless sensor network; centroid localization algorithm; DV-Hop; least mean square error criterion; anchor node deployment strategy

2015-04-05；

2015-07-25 Received date:2015-04-05；Revised date：2015-07-25

国家自然科学基金(No.11302118)；山东省自然科学基金(No.ZR2014FM011)；山东省高等学校科技计划(No.J12LN08)

Foundation Item:National Natural Science Foundation of China(No.11302118);National Natural Science Foundation of Shandong Province(No. ZR2014FM011); Science and Technology Project of Higher Education of Shandong Province(No.J12LN08)

TP393

A

1002-0802(2015)09-1044-09

10.3969/j.issn.1002-0802.2015.09.013

马淑丽(1989—)，女，硕士研究生，主要研究方向为无线传感器网络、无线通信技术；

赵建平(1964—)，男，教授，主要研究方向为无线通信技术。