GF(3)上一类广义自缩序列的伪随机性*

徐玉春，王锦玲

(1.郑州铁路职业技术学院，河南 郑州 450052；2.郑州大学，数学系，河南 郑州 450001)

GF(3)上一类广义自缩序列的伪随机性*

徐玉春1，王锦玲2

(1.郑州铁路职业技术学院，河南 郑州 450052；2.郑州大学，数学系，河南 郑州 450001)

在GF(3)上构造了一类广义自缩序列的新模型，经过分析和计算，证明了新型广义自缩序列的最小周期为:2×3n-1，并对新序列的1长1-游程的个数进行精确的统计，计算出0-游程，1-游程，2-游程的分布非常均衡。研究得出此类新序列不但保持了GF(2)上第四类广义自缩序列良好的伪随机性，而且在此基础上得出一些新的密码学指标，相比之下各项指标都有很大的提高，并与GF(3)上其它广义自缩序列相比具有更好的密码学特性。

广义自缩序列；m-序列；游程；周期

0 引 言

序列密码的设计准则是高度安全和简单结构的统一,首先是Willi Meier[1]提出了自缩序列，因结构简单而引人入胜,颇受关注,随后胡予璞等人又在此基础上给出了广义自缩序列[2-6]的定义,先是在GF(2)上研究了广义自缩序列的很多性质，作为对广义自缩思想的推广，又在GF(q)上研究了此定义下广义自缩序列的许多密码学性质,如0-1分布的均衡性等。而本文则在GF(3)上又讨论一类广义自缩序列的伪随机性质,其优点在于：改变了以往在GF(3)上所讨论的双向输出模型，使输出模型由双向输出到双向组合输出，而且是三项组合，比前人构造的广义自缩序列更加完善，这一突破使得此序列的密码学性质比前人的更具优势[8-11]，如0,1,2游程分布均衡，且最小周期都达到最大2·3n-1。

1 序列b的定义

定义1:设a=a0a1a2…∈GF(3)，a=a0a1a2…为n级m-序列，且周期为3n-1。现有序列b=b0b1b2…，且与序列a=a0a1a2…的关系如下：

如果ak=1,则输出ak-1;如果ak=2,则输出ak-1+ak+1+ak+2;否则不输出;(k=1,2,…)，这样得到的输出序列记为b=b0b1b2… ，称序列b为GF(3)上新一类广义自缩序列。

标记0m是长度为m的0串，其中长度m可以取0；“*” 表示GF(3)上任意值，有上述定义知，2×3n-1为序列b的一个周期。

2 序列b的游程分布

首先考虑序列b的长度为1的1-游程：

引理2.1：设t为以固定整数，满足at=at-1=1，此时对应序列b的一个输出比特bs=at-1=1，若得到序列b的长度为1的1-游程。

当且仅当，在以下7种情形下得到010：

(1)011220(2)011201(3)011211(4)01100m221(5)01100m212 (6)01100m200 (7)01100m1 。

当且仅当，在以下7种情形下得到210：

(1)211220(2)211201(3)211211(4)21100m221(5)21100m212(6)21100m200 (7)21100m1。

当且仅当，在以下6种情形下得到012：

(1)011222(2)011210(3)011201(4)01100m211(5)01100m220 (6)01100m202。

当且仅当，在以下6种情形下得到212：

(1)211222(2)211210(3)211201(4)21100m211(5)21100m220 (6)21100m202。

引理2.2：设t为以固定整数，满足at=2，ak-1+ak+1+ak+2=1，此时对应序列b的一个输出比特bs=ak-1+ak+1+ak+2=1，若得到序列b的长度为1的1-游程。

当且仅当，在以下15种情形下得到010：

(1)222201(2)1220221(3)120201(4)1220212(5)1220200 (6)1202222(7)012210(8)01200m0221(9)01200m0212(10)01200m0200(11)01200m01(12)010m02222(13)0200m02222(14)010m0201(15)0200m0201。

当且仅当，在以下15种情形下得到210：

(1)122201(2)0220221(3)0220212(4)0220200(5)212210(6)21200m0221(7)21200m0212(8)21200m01(9)21200m0200(10)0202222(11)210m02222(12)2200m02222(13)020201(14)210m0201 (15)2200m0201。

当且仅当，在以下16种情形下得到012：

(1)02211(2)222200(3)1220220(4)1220211 (5)1220202(6)012212(7)01212(8)01200m0220(9)01200m0211(10)01200m0202(11)1202221(12)010m02221(13)0200m02221(14)120210(15)010m0210 (16)0200m0210。

当且仅当，在以下16种情形下得到212：

(1)22211(2)122200(3)0220220(4)0220211 (5)0220202(6)212212(7)21212(8)21200m0220(9)21200m0211(10)21200m0202(11)0202221(12)210m02221(13)2200m02221(14)020210(15)210m0210 (16)2200m0210。

定理2.1：设序列b1的长度为1的1-游程的个数为u，则：

72×3n-6-22≤u≤72×3n-6+23

以同样的分析方法可得：

定理2.2：设序列b的长度为1的0-游程的个数为u，则:

72×3n-6-24n+124≤u≤72×3n-6+58n-164

定理2.3：设序列b的长度为1的2-游程的个数为u，则:

72×3n-6-30≤u≤72×3n-6+22

3 序列b的最小周期

引理3.1：设b为输出序列，在b的一个周期P内，若有一s长1-游程出现的次数为N，且满足gcd(N,P)=1，则称P是序列b的最小周期。

证明：参见文献[7]。

为了得到序列b的最小周期，由序列b游程分布可得：

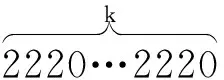
引理3.2：当k≥1；m≥1时，若输出序列b中出现n+3k长的1-游程时，m-序列a中有以下几种情况出现：(其中n-3m-2≥0)

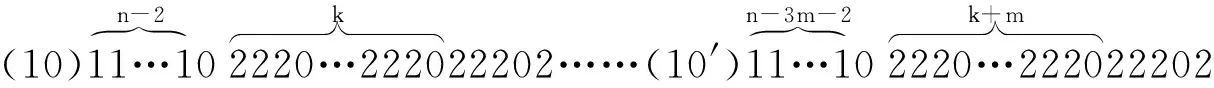
定理3.1：序列a为m-序列，由a控制输出的序列b有最小周期:2×3n-1。

证明：根据输出序列的形式，知2×3n-1是输出序列b的一个周期，又因m-序列a中没有大于n长的1-游程，故考虑以下几种情况：若序列b在一个周期2×3n-1中，出现了n+3k长的1-游程，则一定是在引理3.2中m-序列a控制输出的所有比特串中出现，因m-序列a中n长1-游程仅出现一次，故比特串200

4 结束语

先列出GF(3)上几类广义自缩序列的输出序列与本文的一类广义自缩序列在最小周期都达到2×3n-1内的游程分布情况表。

表1

从表上可以看到本文构造的一类广义自缩序列长游程少，0，1，2游程分布均匀，研究表明：由驱动序列a生成的广义自缩序列b其优点在于，序列b对序列a的保护强度高，而且暴露的驱动信息少，适合在通信和计算机编码系统的应用。

[1] W Meier,Stafflebach O.The Self-Shrinking Generator[A]. Advanced in Cryptology-Eurocrypt,94,1994:205-214.

[2] HU Y P，XIAO G Z. Generalized Self-Shrinking Generator[J]. IEEE, Trans on Inform Theory, 2004, 150(4):714-719.

[3] 董丽华,高军涛,胡予璞.一类广义自缩序列的伪随机性[J].西安电子科技大学学报(自然科学报),2004,31(3):394-398. DONG Li-hua,GAO Jun-tao,HU Yu-pu. Pseudo-Random ness of the First Generalized Self-Shrinking Sequences[J]. Xi'an University of Electronic Science and Technology Journal (Natural Science),2004,31(3):394-398.

[4] 胡予璞,张玉清.新一类广义自缩序列的最小周期[J].通信学报,2003,24(6):169-176. HU Yu-pu, ZHANG Yu-qing. A New Class of Generalized Self Shrinking Sequences of the Minimum Period [J].Journal of Communications,2003,24(6):169-176.

[5] 胡予璞,白国强,肖国镇.GF(q)上的广义自收缩序列[J]. 西安电子科技大学学报(自然科学报),2001,28(1):5-7. HU Yu-pu, BAI Guo-qiang, XIAO Guo-zhen. Generalized Self Shrinking Sequence of GF (q) [J]. Journal of Xi'an Electronic and Science University (Natural Science), 2001, 28 (1): 5-7.

[6] 胡予璞,肖国镇.第四类广义自缩序列的伪随机性.中国科学(E辑),2003,33(10):896-905. HU Yu-pu, XIAO Guo-zhen.The Pseudo Randomness of the Fourth Class Generalized Self-Shrinking Sequences.Chinese Science (E), 2003, 33 (10): 896-905.

[7] 万哲先.代数与编码.北京:机械工业出版社.2002. WAN Zhe-xian. Algebra and Coding. Beijing: China Machine Press.2002.

[8] 王锦玲,徐玉春.GF(3)上若干类广义自收缩序列的伪随机性[J].通信技术,2011,44(5):54-56. WANG Jin-ling, XU Yu-chun. Pseudo-Randomness of Some Generalized Self-Shrinking Sequences on GF(3)[J]. Communications Technology, 2011,44(5):54-56.

[9] 董乐,王锦铃,陈铁生.广义自收缩序列特例的扩展[J].信息安全与通信保密,2006,152(8):78-82.

DONG Le, WANG Jin-ling, CHEN Tie-sheng. Extension of Generalized Self-Shrinking Sequences[J].Information Security and Communications Privacy,2006,152(8):78-82.

[10] 龚吕乐.GF(3)上新一类广义自缩序列及其扩展[D].郑州大学硕士学位论文,2010：5. GONG Lv-le. A Special Generalized Self-Shrinking Sequence on GF (3) and Its Extension[D].Zhengzhou University Degree Thesis,2010：5.

[11] 王慧娟,王锦铃,龚吕乐. GF(3)上第四类广义自缩序列[A].密码学进展-中国密码学会2009年论文集,Science Press USA Inc,2009:58-63. WANG Hui-juan, WANG Jin-ling, GONG Lv-le. Generalized Self-Shrinking Sequences of Fourth Classes of GF(3)[A].Advances in Cryptography-the 2009 Paper Collection of the China Cipher Society,Science Press USA Inc,2009:58-63.

Pseudo-Randomness of New Generalized Self-shrinking Sequence on GF(3)

XU Yu-chun1, WANG Jin-ling2

(1.Zhengzhou Railway Vocational and Technical College, Zhengzhou Henan 450052,China; 2.Department of Mathematics, Zhengzhou University, Zhengzhou Henan 450001,China)

New model of a generalized self-shrinking sequence is constructed, based on this new model, the analysis and calculation indicates that the minimum cycle of this new-type generalized self-shrinking sequence is 2×3n-1.Accurate statistics is also done on the number of new sequences 1 long 1-pattern, and calculation shows that the 0-pattern, 1-pattern, 2-pattern are in very balanced distribution. Research indicates that such new sequences over GF (2) on the fourth class of generalized self shrinking sequences have fairly good pseudo-randomness, some new indicators of cryptography are drawn, and all are relatively improved. The new self-shrinking sequence on GF(3) keeps very good pseudo-randomness, and as compared with other self-shrinking sequences,has much better crypto properties.

generalized self-shrinking sequence; m-sequence; run distribution; cycle

2015-04-01；

2015-07-28 Received date:2015-04-01；Revised date：2015-07-28

河南省教育厅自然科学指导性计划项目(No.200510459003)

Foundation Item:Natural Science Guiding Program of Education Office of Henan Province(No.200510459003)

TN918.4

A

1002-0802(2015)09-1078-04

10.3969/j.issn.1002-0802.2015.09.019

徐玉春(1986—)女，硕士，助教，主要研究方向为代数与密码学;

王锦玲(1963—)女，硕士，副教授，主要研究方向为代数与密码学。