基于HHT 的电力负荷组合预测模型研究与应用

蒋建东，张豪杰，王 静

(1．郑州大学 电气工程学院，河南 郑州450001;2．济源供电公司，河南 济源459000)

0 引言

提高预测精度对保证系统的安全、经济运行有重要意义．电力负荷序列具有周期性和较强的随机性，是一种非线性、非平稳、拟周期性的随机序列［1］．HHT(希尔伯特黄变换)方法对处理非平稳、非线性序列有清晰的物理意义，使信号分解具有唯一性和良好的局部化特性．

文献［2］中利用HHT 算法将历史负荷分解，利用多神经网络组合方法进行预测，取得了较高的预测精度． 文献［3］将分解后的分量重新组合得到3 个分量，再用不同的模型分别预测． 文献［4］将EMD 方法应用于振动信号的趋势预测，利用单一的最小二乘支持向量机模型预测全部子序列，未考虑各分量的特点． 文献［5］将HHT 算法用于对地震资料的分析．

笔者对电力负荷本身及其影响因素进行分析，结合HHT 算法以及不同预测模型各自的优势，构造出新的组合预测模型，在对中、高频分量的预测中，考虑了与负荷密切相关的温度因素［6］．该组合模型在电力负荷预测中能实现各种模型间的优势互补，更具合理性，通过实际算例证明了模型的有效性［7］．

1 HHT 算法简介

HHT 算法是用于处理非线性、非平稳信号的一种全新信号处理方法，由美籍华人N．E．Huang等人提出．该算法首先采用EMD 算法将原始序列分解为频率不同的若干IMF(固有模态函数)分量之和，然后对每个IMF 分量进行Hilbert 变换得到瞬时频率，是一种具有自适应性的时频分析方法［8］，其计算结果与小波分析方法类似． 但是，该方法避免了小波基选取的困难，更适合用于处理非线性、非平稳信号．

HHT 算法已经在电力工程中成功应用于谐波分析、故障测距、电能质量检测等领域，在地震学、生物医学等学科中的应用也取得了良好的效果．然而，该方法在电力负荷预测中的应用还处于初步发展阶段，有长远的发展前景．

2 模型的建立

结合负荷序列自身的特点，笔者采用EMD 算法将电力负荷序列分解为不同频率的IMF 和r(残余分量)之和，再对各分量做Hilbert 分析，根据各分量特点，选取RBF 神经网络、BP 神经网络和时间序列模型分别进行预测，最后将各分量的预测结果相加，得到最终预测值［9］．

2．1 HHT 算法原理

首先对负荷数据进行分解，得到一组固有模态函数IMF1，IMF2，IMF3…和残余分量r．对于负荷时间序列x(t)，分解为n 阶，x(t)可表示成如下形式

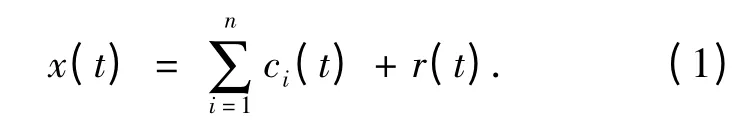
式中:ci(t)为第i 个IMF 分量;r(t)为残余函数．

其经验模态分解流程如图1 所示．

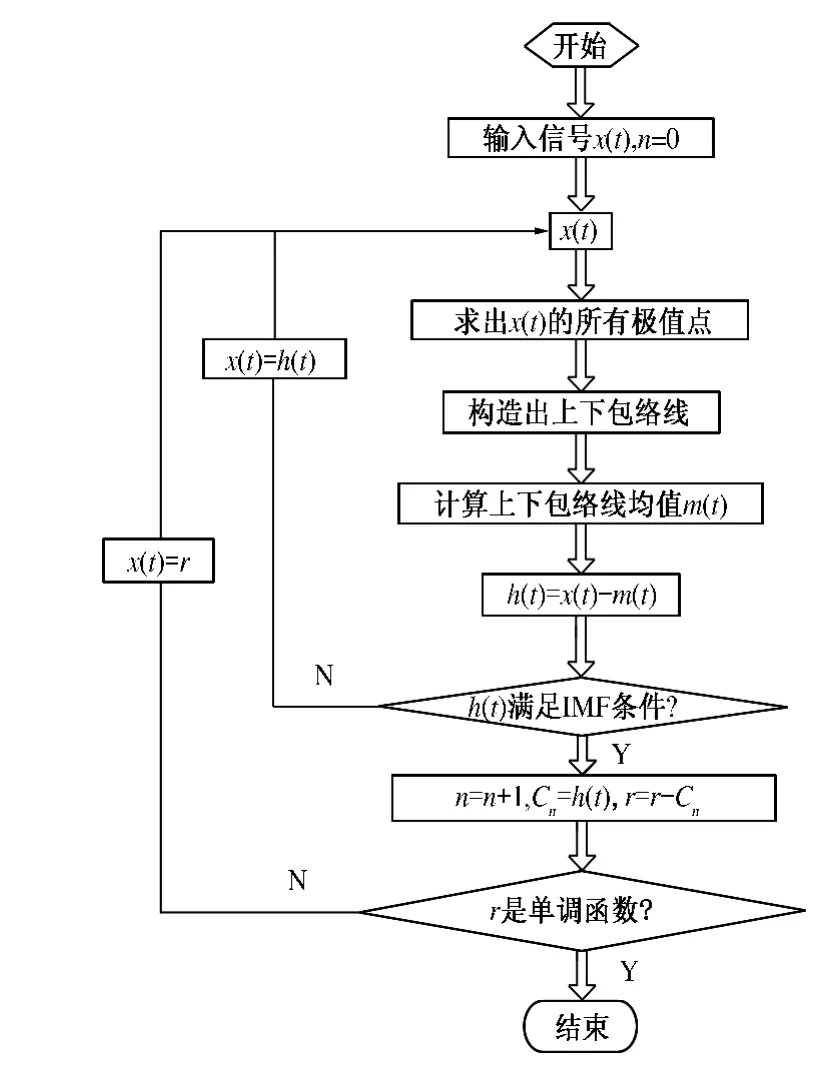
图1 经验模态分解流程图Fig．1 EMD Flow chart

然后对分解后的每个固有模态函数序列进行Hilbert 变换，求得各序列的瞬时频率，其过程如下．

对每个固有模态函数分量作Hilbert 变换可得数据序列

由此可以构成一个复序列:

其中，ai(t)为幅值函数;φi(t)为相位函数，适的模型对不同频率分量分别进行预测．

2．2 RBF 神经网络模型

径向基函数(RBF)神经网络是一种3 层前向型的网络结构，包括输入层、隐含层和输出层，其神经元模型如图2 所示．RBF 神经网络结构简单，能够实现快速学习，并能以任意精度逼近复杂函数，在时间序列分析和图像处理等领域得到了广泛的应用．

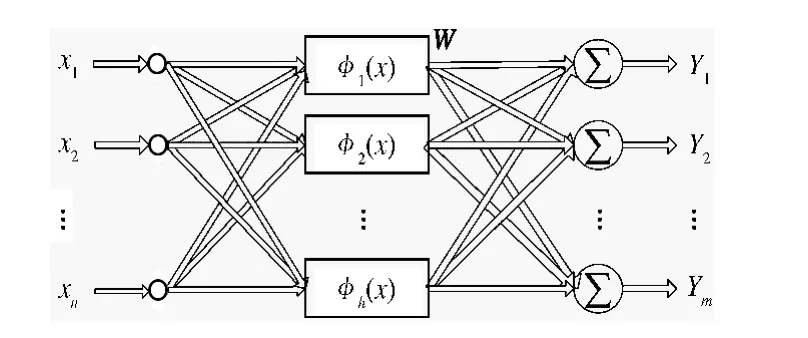
图2 RBF 神经元模型Fig．2 RBF Neuron Model

该模型有n 个输入，h 个隐节点，m 个输出，x =(x1，x2，…，xn)T为网络输入矢量，Φi(x)为第i个隐含层节点的激活函数，W 为输出权矩阵．高斯函数的形式简单，理论分析相对容易，存在任意阶次导数，因此笔者选取高斯函数作为径向基函数为

式中:δ 为扩展常数，其值越小，RBF 的宽度就越窄，径向基函数就越具有选择性． 此时，隐含层及节点i 的输出为

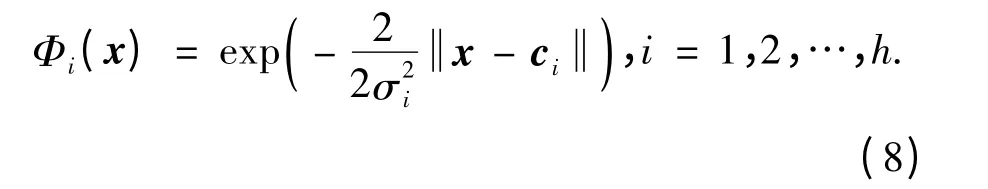
式中:x 是输入向量;σi为第i 个基函数的归一化因子，表征基函数的宽度;ci为第i 个基函数的中心，与x有相同维数;x-ci是x与ci的距离．Φi(x)在ci处只有一个最大值，并随x-ci的增大，Φi(x)迅速衰减到零;m 是隐含层节点数，RBF 神经网络的输出为

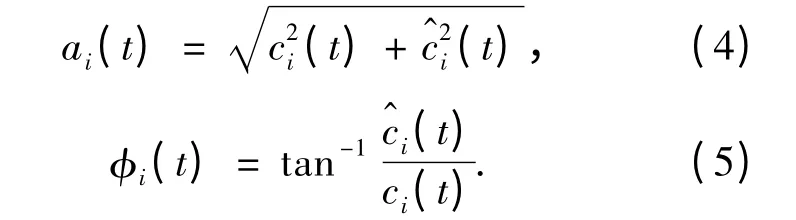
由式(5)可得到瞬时频率为

对各IMF 分量的频率特性进行分析，选取合

RBF 神经网络预测模型能将输入层到隐含层的非线性映射转变成另一个空间上的线性映射，学习速度快，对于频率较高、波动性较大和随机性较强的信号预测效果较好．

2．3 BP 神经网络模型

BP 算法结构简单，基本思想是最小二乘法，主要由模式顺传、误差反传、反复记忆和学习收敛4 个过程组成［10］． 选取n 个样本x(1)，x(2)，…，x(n)，用其中的m 个观测值作为样本，预测n + 1个样本的值x(n +1)，BP 网络训练和预测的步骤为:

首先，把x(1)，x(2)，…，x(n)分成k 组，每组有m +1 个值，前m 个值为网络输入，后一个为输出节点的期望值;

其次，利用神经网络的BP 算法对网络进行训练;

最后，将x(n - m + 1)，x(n - m + 2)，…，x(n)作为输入，利用训练完成后网络的连接权值求出预测值x(n +1)．

BP 神经网络模型函数逼近能力较强，适用于预测周期性较强、随机性较弱、相对平稳的时间序列．

2．4 时间序列模型

首先用所分析的时间序列建立一个模型，然后进行参数估计，再用所建模型来计算时间序列的预测值． 时间序列的自回归AR(p)模型，其形式为:

式中:p 为模型阶次，可采用BIC 准则确定;φi(i =1，2，…，p)为自回归系数，φ 是模型的待估计参数，利用最小二乘法进行参数估计;εt为白噪声序列［11-12］．

自回归AR(p)模型简单，预测速度快，缺乏自学能力，适合用于预测变化规律简单、频率较低、趋势性强的时间序列．

3 负荷影响因素分析

日趋复杂的负荷特性，使对负荷本身及其影响因素分析的重要性也日益突出． 在电力负荷预测中，充分考虑电力负荷影响因素有利于提高预测精度．电力负荷受到经济、政治、气象、电价等因素的影响，其中气象因素最为明显．对负荷产生影响的气象因素包括温度、湿度、气压、风速、降雨量等，其中温度对负荷的影响最为突出．

随着人民生活水平的提高，降温取暖负荷在总负荷中的比重呈增大趋势，在很大程度上影响着负荷水平．由图3 中温度曲线和负荷曲线可以看出，温度与负荷呈明显的正相关性．

因此，在进行负荷预测的过程中考虑温度与负荷的相关性，对短期电力负荷预测具有极其重要的意义．本方法在中、高频分量预测模型中考虑了温度因素的影响．

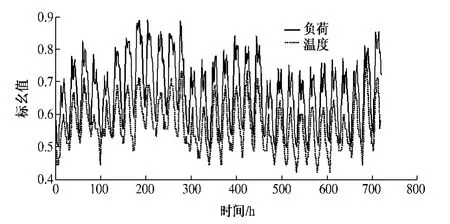
图3 温度和负荷的标幺曲线Fig．3 Curve of temperature and load

4 算例分析

选取河南某地区2012 年8 月1 日到8 月30日典型的夏季负荷每天24 点数据作为训练样本，来预测8 月31 日一天的负荷．

首先，利用HHT 算法对处理后的数据做经验模态分解，得到5 个固有模态函数IMF1 ～IMF5和一个残余分量r，结果如图4 所示．

图4 经验模态分解Fig．4 Empirical mode decomposition

再用HHT 算法对各个固有模态函数做Hilbert 变换，求得各分量的时频谱，如图5 所示．

各分量的平均瞬时频率如表1 所示． 从表1中可以看到，经过EMD 分解得到的固有模态函数频率逐渐降低，各分量的平均频率成近似二倍关系依次减小．IMF1、IMF2 频率较高，随机性强，主要是负荷的随机性成分，选用RBF 神经网络模型进行预测;IMF3，IMF4 频率相对较低，周期性强，主要是负荷的周期性成分，选取BP 神经网络方法建模进行预测;IMF5 和残余分量r 频率接近为零，主要是负荷的趋势性成分，选取时间序列法中的自回归AR(p)模型进行预测．最后将各个分量的预测值相加得到最终的预测结果．

图5 各IMF 分量瞬时频率Fig．5 Instantaneous frequency of each IMF

表1 各IMF 分量平均频率Table 1 The average frequency of each IMF

采用两种模型分别进行预测，模型一中不考虑温度对负荷的影响，模型二中在RBF 神经网络模型和BP 神经网络模型考虑温度的影响，由该组合模型得到的预测结果如图6 所示［13］．

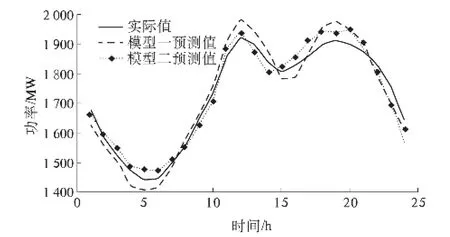
图6 预测值与实测值对比Fig．6 Comparison of predicted value and measured value

采用上述所建立的组合预测模型，以2012 年8 月31 日24 点的负荷值作为预测样本进行预测精度分析，分析结果如表2 所示． 由表2 分析可知，模型一所得预测结果符合负荷预测的一般要求，考虑了气温影响的模型二所得预测结果的精确度更高，效果更好，证明了该组合模型具有较高的预测精度．

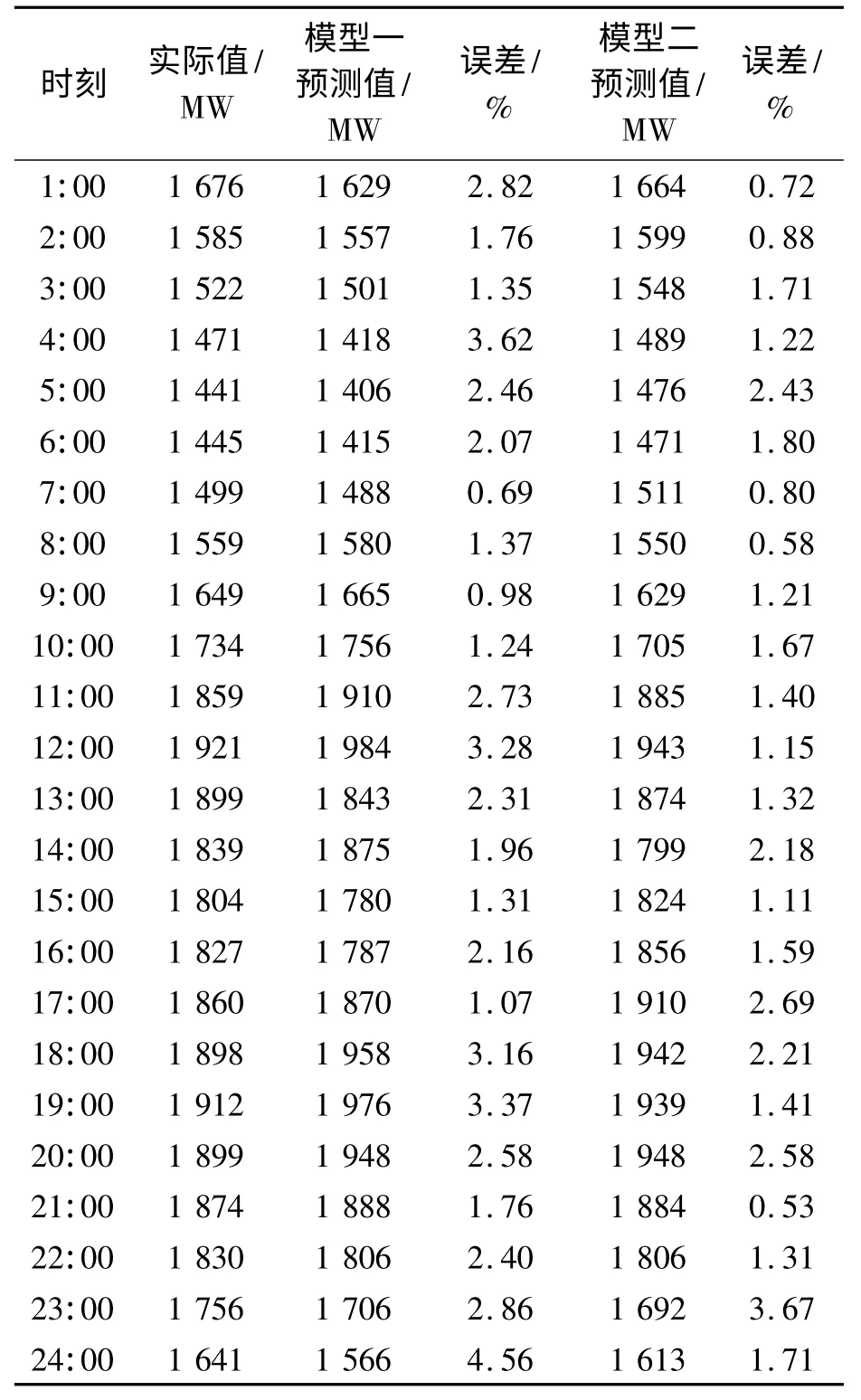
表2 预测结果分析Tab.2 Predications analysis

5 结论

笔者根据电力负荷的特点，提出了一种基于HHT 的负荷组合预测模型．该模型首先利用EMD方法将原始负荷序列进行分解，然后根据分解后各子序列的特点，分别选择RBF 神经网络、BP 神经网络和时间序列模型进行预测，并在中、高频分量预测模型中考虑了温度因素的影响． 最后将各子序列的预测结果相加得到负荷预测值． 实际算例表明，笔者所提出的预测方法能有效提高预测精度，证明了该模型的有效性．

［1］ 康重庆，夏清，刘梅．电力系统负荷预测［M］．北京:中国电力出版社，2007:2 -63．

［2］ 白玮莉，刘志刚，彭权威，等．基于HHT 和神经网络组合的负荷预测模型研究［J］． 电力系统保护与控制，2009，37(19):31 -35．

［3］ 李媛媛，牛东晓，乞建勋．基于经验模式分解的电力负荷混合预测方法［J］． 电网技术，2008，32(8):58-62．

［4］ 王洪波，朱启兵． 基于EMD 和LS -SVM 的非平稳振动信号趋势预测［J］． 计算机工程与应用，2008，44(16):157 -159．

［5］ 曹思远，邴萍萍，路交通，等．利用改进希尔伯特—黄变换进行地震资料时频分析［J］． 石油地球物理勘探，2013，48(2):246 -254．

［6］ 段其昌，饶志波，黄大伟，等． 基于EMD 和PSO -SVM 的电力系统中期负荷预测［J］． 控制工程，2011，19(5):913 -917．

［7］ 刘兴茂，何正友． 基于希尔伯特-黄变换的输电线路距离保护方案［J］． 电力系统自动化，2013，37(2):108 -112．

［8］ 束洪春．电力工程信号处理应用［M］．北京:科学出版社，2009:323 -362．

［9］ 王小波，刘德强． 基于神经网络的短期电力负荷预测的研究［J］．电力学报，2011，26(4):287 -289．

［10］周德强，武本令．灰色BP 神经网络模型的优化及负荷预测［J］．电力系统保护与控制，2011，39(21):65-69．

［11］YANG Hong，HUANG Chao-ming． A new short load forecasting approach using self organizing fuzzy ARMAX models［J］． IEEE Transactions on Power Systems，1998，13(1):217 -225．

［12］万志宏．基于时间序列的电力系统短期负荷预测研究［D］．广州:华南理工大学电力学院，2012．

［13］罗勇，郑金，宁美凤．短期电力负荷组合预测方法研究［J］．郑州大学学报:工学版，2013，34(1):78 -81．