动态转化 自主整理

王小芳

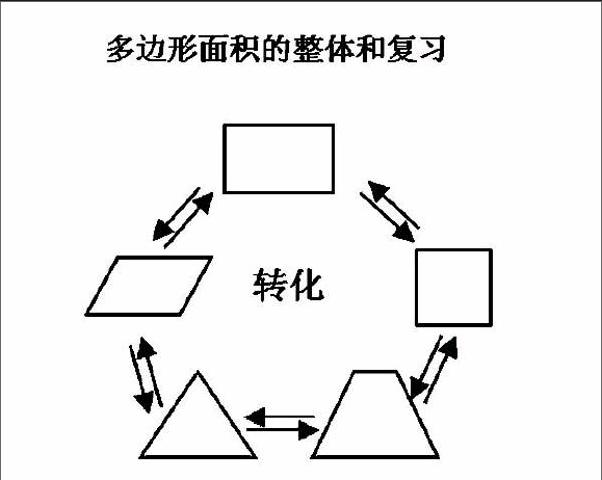
几何初步知识的整理复习应注重整理、沟通、深化、提升。整理和复习多边形面积时，除了知识的巩固深化和运用，还要注重方法习得和能力提升。引导学生自主整理，拓展视野，动态转化，在“动”中求“静”，在“静”中探求“动”的规律，为学生今后进一步学习动态几何奠基。

【教学再现】

一、设置情境，引入课题

师：同学们，第29届奥运会在哪儿召开的？（北京）是的，北京奥运会向世界展示了运动健儿们高超的竞技水平，展示了中国人民热情好客的精神风貌，还展示了雄伟壮观的运动场馆（课件—鸟巢），这些运动场馆凝聚着中国人民的智慧和才华。让我们一起来欣赏。

师：这些雄伟的建筑物里蕴藏着丰富的数学知识，其中也有我们学过的平面图形的知识。（出示课件）回顾一下，我们已经学会了计算哪些平面图形的面积呢？

生：长方形、正方形、三角形、梯形、平行四边形面积的计算。

（随学生的回答，教师在黑板上出示图形）

师：是啊，我们已经学习了这些平面图形面积的计算，现在你们还存在哪些问题？

生1：组合图形面积计算困难。

生2：对公式的推导过程理解不透彻。

……

（学生回答，教师板书）

师：为了解决这些问题，同时让我们把这一单元的知识掌握得更有条理、更牢固，这节课，我们一起来整理和复习“多边形面积”的知识。（板书“多边形面积的整理和复习”）

二、自主整理，交流汇报

（一）分组活动

师：请每一组的同学先一起讨论整理方法，再分工合作，推荐一人记录讨论结果，1～2人汇报。整理前请先看看老师的提示。（课件出示）

温馨提示：

A.可回顾每种平面图形面积公式的推导过程来梳理所学的多边形面积的知识。

B.可根据图形之间的联系整理多边形面积的知识。

C.整理时要有条有理、层次分明、简洁明了。

（二）汇报交流

师：谁愿意把你们组的整理的方法给大家展示一下

<F：＼TM＼中小学＼2015＼2期＼t1q-40.tif>

……

师：真了不起，出现了这么多的整理方法，你们对这些整理方法有什么看法？

生1：第一种方法好，很清楚。

生2：第二种方法好，不仅整理了所学的图形面积公式，还整理了公式的推导过程。

生3：有的组只整理了面积公式，如果能整理公式的推导过程就好了。

……

（三）动态联系

师：同学们善于发现他人的优点，还能提出合理的建议，这是一种良好的学习品质。很多组的同学都

整理了面积公式，有的组还整理了公式的推导过程。平行四边形、三角形、梯形的面积公式分别是怎样得到的？

（教师根据学生的回答，课件展示平行四边形、三角形和梯形的面积公式的推导过程）

师：刚才，有的组整理了我们学过的平面图形与多边形之间的关系，其实这些图形之间还隐藏着一些秘密，想不想知道？（课件演示）

（1）当这个梯形上底的长度为0

时，这个梯形变成了什么图形？

生：三角形

（2）怎样才能使这个梯形变成一个平行四边形？

生1：缩短下底和上底一样长。

生2：延长上底和下底一样长。

生3：只要把上底、下底变成

一样长……（课件演示）

师：通过这样的变化，你发现了它们之间的秘密了吗？

生1：图形之间是相互联系的。

生2：图形之间在特定的情况下可以互相转化……

师：三角形、平行四边形、梯形之间有着密切的联系，在特定的情况下可以互相转化，那么长方形、正方形和这些平面图形之间可以互相转化吗？

师：转化是一个非常重要的数学思想，在我国古代，数学家刘徽就已经用这种思想来解决问题了，让我们一起来看一看。

出示课件：

<F：＼TM＼中小学＼2015＼2期＼t1q-43.tif>

三、巩固深化，解决问题

1.师：你能正确选择算式吗？

有三块菜地（如图所示），农民伯伯准备在上面种三种蔬菜，它们的面积分别是多少？请选择正确的计算方法。

<F：＼TM＼中小学＼2015＼2期＼t1q-44.tif>

<F：＼TM＼中小学＼2015＼2期＼t1q-48.tif>

师：列式要注意什么？

生：注意弄清底和高的对应关系，计算三角形梯形面积不要忘记除以2。

2.师：前面有同学提到计算组合图形的面积有困难，通过刚才的复习我相信你们一定能计算下图的面积。（出示课件）

学生独立完成、展示汇报。

师：计算组合图形的面积，你

有什么好的建议？

生：把它割补成学过的平面图形来计算。

生：先观察整体，再思考可以割补成学过的什么平面图形，最后计算。

师：利用转化的思想把未知的问题转化为已知的方法，然后解决问题。数学学习中常常“化新为旧”能使数学问题“化繁为简”和“化难为易”。

3.和平广场有一块空地，如图。

已知三角形的面积是1400m2。

①你能求出三角形的高吗？

②政府准备绿化这片土地，种植1平方米的草坪需200元，算一算要绿化这片草地需多少钱？

四、全课总结，提炼升华

师：生活中许多事情的解决都需要转化，特别是比较复杂的事，可以通过别人的帮助就会转化成比较简单的事情，问题就会迎刃而解。

板书设计：

<F：＼TM＼中小学＼2015＼2期＼t1q-47.tif>

【课后反思】

本节课注重学生已有的生活经验和知识基础，为了达到“查漏补缺，系统整理，巩固提高”的教学目的，科学地设计并成功地实施了教学。教学中学生合作

探究，积极思考，大胆陈述，有效参与。

一、联系旧知，针对问题整理复习

本课整理复习以学生提出的“组合图形面积计算困难和对公式的推导过程理解不透彻”这两个问题为导向展开，教学充分体现了“以问题为中心”，重视学生思维的方向性和有序性，使整理复习更有针对性和实效性。教学首先让学生提出还存在的问题，再根据问题分组梳理、独立陈述、评价交流、补充完善，形成本单元知识的面，理顺认知。然后引导学生动态联系，梯形在特定条件下转化为三角形、长方形或平行四边形。学生清楚地看到这几种平面图形之间的变化，深刻理解了几个面积公式之间的关系，把枯燥的公式记忆置于动态变换的几何演示之中，较好地让学生感受了动态几何观念，体悟到了静中之动、动中变化、变中之不变的事理。学生在合作交流中从不同的角度对知识进行了整理，进一步理解了割补、平移的转化思想，在比较与评价中不仅理解了不同的整理方法，而且还上升到了评鉴的高度，较好地体现了系统整理，巩固提高的教学要求。

二、注重“转化”，适时渗透解题策略

数学思想方法是数学学科实施素质教育的一项重要内容，它在培养学生数学思维能力，提高学生的素质方面具有极为重要的作用。本课从“公式的推导——平面图形之间的关系——解决问题”都渗透了“转化”这一重要的数学思想，有利于学生形成问题解决策略。其实，万事都需转化，或易或难。数学“教学”应上升到数学“教育”，情理法并重，才能学以致用。

三、尊重差异，关注解法灵活多样

学生是有差异的。在教学中，让学生用不同方式整理和复习，用不同方法计算多边形面积，从不同视角思考图形的转化，让学生谈感受，评优劣，总结复习方法，归纳组合图形面积计算的解题策略，深化认识，强化认知，展示个性。

总之，全课把知识掌握、技能形成和文化传播紧密地揉合在一起，以知识的整理复习为主线，通过练习，较好地让学生的能力随教学进程而发展，恰当地穿插数学文化，拓展学生视野，孕伏未来发展所需。以数学之法，析百事之理，解生活问题，行人生之路，这才是数学教育之真谛。（责任编辑：李雪虹）