GERG气体摩阻系数方程及其显式化公式
苑伟民
中国石化天然气分公司广西液化天然气工程项目部,广西北海536000
GERG气体摩阻系数方程及其显式化公式
苑伟民
中国石化天然气分公司广西液化天然气工程项目部,广西北海536000
预测天然气管道中天然气的流动,一个关键的问题是为摩阻系数λ的计算选择合适的公式,Colebrook-White方程并不是一个适用于所有流态的普适化摩阻系数计算公式。介绍了新的气体摩阻系数GERG方程,该方程的适用范围较宽,计算时在一定情况下可以替代著名的Colebrook-White方程、Zegarola关联式;并可根据已知的数值,通过调整方程的参数,得出目前所有典型摩阻系数方程给出的计算值。但GERG方程为摩阻系数λ的隐式方程,求解过程较复杂,因此提出了该方程的显式形式,显式公式的验证计算表明:新公式的精确度较高,计算时间相对较短,可避免隐式方程求解的迭代算法。
天然气流动;摩阻系数;GERG方程;显式公式
AGA10号报告《天然气和其他相关烃类气体中的声速》收集的管道操作数据表明,测量的传输系数和通过Colebrook-White公式计算得到的数值有很大的差别[1]。这些测量结果还表明传输系数作为雷诺数的函数具有一定的差异性。根据数据做出的传输系数曲线显示了以下特征:
(1)雷诺数较低时,传输系数曲线不符合光滑管流曲线变化规律,而是几乎与光滑管流曲线平行。
(2)位于某个“临界”雷诺数时,传输系数曲线变成了符合完全粗糙管流曲线的平行线。值得注意的是,由光滑管流到完全粗糙管流的曲线变化是一个突变(点跳跃),而Colebrook-White公式所描述的曲线是一个缓慢的变化过程。
除低雷诺数区之外,天然气管道的实际操作数据与Colebrook-White公式预测的数据相比偏离最高值达6%,这在实际工程中是不允许的。
1 GERG方程
Colebrook-White方程不是在所有情况下都可准确计算摩阻系数的方程。Leif Idar Langelandsvik,Willy Postvoll和Preben Svendsen等人对挪威大陆架(Norwegian ContinentalShelf)管道进行的实验给出了摩阻对输量计算结果的影响,实验中低流速将会带来保守的输量计算结果,因为摩阻系数的减小比Colebrook-White方程预测的要快,并且摩阻系数的数据并未落在合理的Colebrook-White曲线内[2]。
2002年,Dr John Piggott,Norman Revell和Dr Thomas Kurschat等人在GERG(Groupe Europeen de Recherches Gazieres)的赞助下[2-3],研究提出了GERG方程:

式中λ——Darcy-Weisban摩阻系数;
k——管道内壁粗糙度/m;
n——幂指数,描述从光滑管到粗糙管转变的剧烈程度;
f——阻力因子(等同于输送效率);
Re——雷诺数。
2 GERG方程的特点
(1)对于完全粗糙流态(例如对于非常大的雷诺数),式(1)和Colebrook-White公式是一致的。
(2)f也称为“气流因子”,气流因子f与“管道效率”密切相关。这个因子为在相同雷诺数下,f≠1和f=1时传输系数的比值。气流因子f描述了由于来自完全发展的管流(f=1)偏差导致在光滑管(k=0)中产生的额外损失。这些额外损失主要是由管流的压力、温度和速度场下的管轴向曲率或其他不对称造成的次要流动产生的。
据相关数据显示,2017年我国道路交通运输安全事故一次死亡10人以上的重大交通事故,从2004年的55起,降低到2016年的11起,安全管理工作获得了不错的成绩。虽然道路交通事故降幅比较明显,但是事故依旧高发。目前,中国道路交通事故年死亡人数排列世界第二。交通事故总量较大,事故起数占全国重特大事故总量的70%;死亡人员占比为80%。因此,加强安全管理工作,具有重要意义。
(3)对于水力光滑区(粗糙度k=0)f=1,公式退化为Zagarola等人提出的传输系数定律[4],这一定律是基于3.2×104<Re<3.5×107的实验数据,由普林斯顿大学在1998年所做的实验得到的。对于水力粗糙管,当f=1时,GERG公式同样退化为Zagarola方程。
(4)当f=1时,不仅在光滑管的情况下可以简化为Zagarola公式,而且在低雷诺数时的粗糙管流也可简化为这一公式。
(5)GERG公式中k=0时,可以通过将Zagarola公式中的替换为,即可得到GERG公式。
(6)参数n与流体是光滑流态还是完全粗糙流态没有关系。然而,该参数在从光滑流到粗糙流的过渡中起着很重要的作用。n=1时为平稳过渡,这与Colebrook-White公式描述的一样。另一方面,前述的“点跳跃”在n=10时可以得到很好的描述。
3 显式GERG方程
3.1 显式方程的提出

式(2)的相对误差数量级约为0.1%,可以根据工程需要使用。
通过对文献[4-7]的研究,提出了式(3)~(5)3个显式GERG方程,并将提出的显式方程与式(1)、式(2)的计算结果、计算时间进行了对比。


式(3)的相对误差数量级在10-4%~10-7%范围内,可以满足设计及工程计算需要。
如果需要更精确的结果,可做进一步推导得到式(4),式(4)的相对误差数量级在10-10%~10-13%。

如果还需要更精确的结果,可进一步推导得到式(5),式(5)的相对误差数量级在10-11%~10-15%范围内。
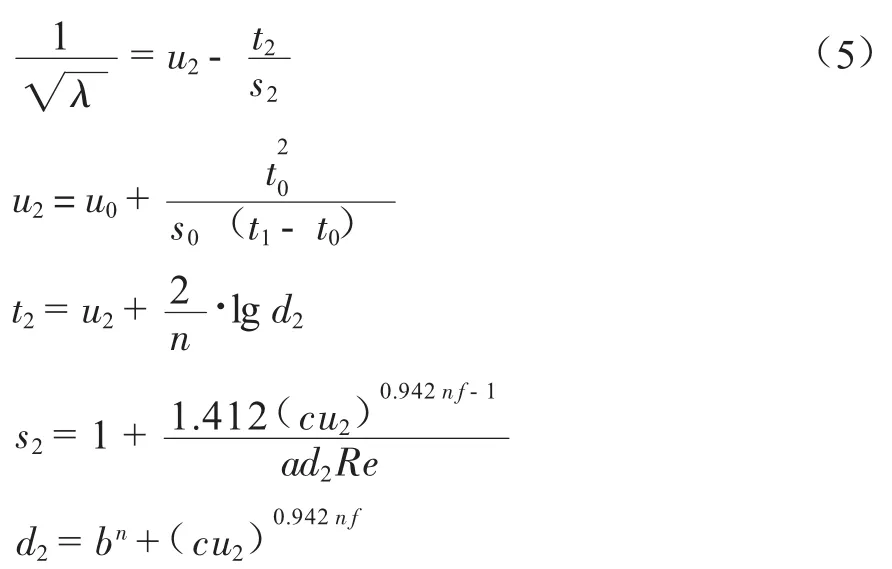
3.2 误差分析
误差分析见图1。
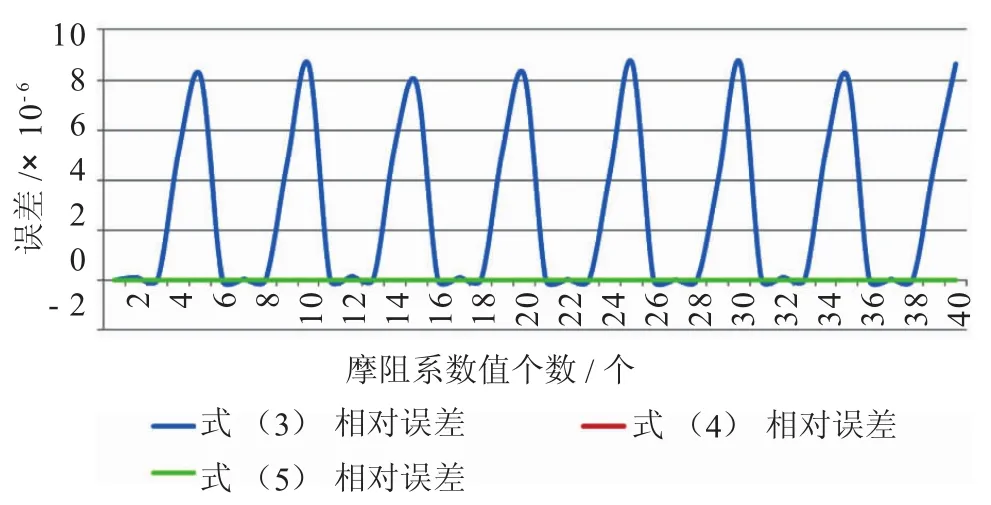
图1 相对误差
从图1可以看出,三个公式的计算结果都较为精确,式(4)和(5)相对误差曲线紧贴横轴,式(5)相对误差最小,式(3)相对误差小于9×10-4%。
4 计算对比分析
4.1 计算实例
计算数据见表1,取GERG方程中参数n=1,f= 1进行求解。

表1 管道的实际运行数据
4.2 结果分析
将式(2)~(5)的计算结果、计算时间与精确值进行对比。以MATLAB R2012a内置函数的计算结果为精确值进行精度对比,结果见表2。
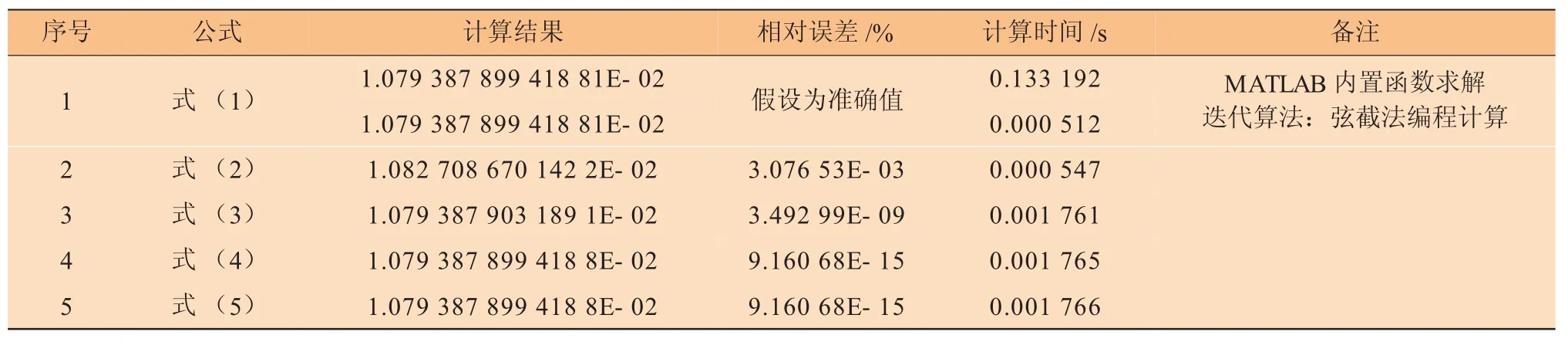
表2 计算结果及计算效率
5 结论
(1)采用文献[1]推荐的显式公式(2)进行计算,速度较快,但是计算误差较大。
(2)公式(3)、(4)、(5)的精度均比较高,但是公式(3)的形式简单,计算较为简便。
(3)显式公式的提出给工程计算提供了较为便捷的数值解计算方法,有利于提高计算效率。
[1]GERSTEN K,PAPENFUSS H D,KURSCHAT T,et al.New transmission factor formula proposed for gas pipelines[J].Oil &Gas Journal,2000,98(7):58-62.
[2]JOHN P,NORMAN R,THOMAS K.Taking the rough with the smooth——a new look at transmission factor formulae[C] //PSIG AnnualMeeting.PSIG,2002:1-21.
[3]BROWN G O.The history of the Darcy-Weisbach equation for pipe flow resistance[C]//Environmental and water resources history,ASCE Civil Engineering Conference and Exposition 2002.Washington D C:ASCE,2002,126(4):34-43.
[4]王小尚,苑伟民.计算隐式摩阻系数方程数值解的简便方法[J].石油工程建设,2014,40(5):70-72.
[5]苑伟民.显式Colebrook-White摩阻系数方程[J].天然气与石油,2013,31(1):17-19.
[6]苑伟民,青青,袁宗明,等.Colebrook-White方程显式公式对比研究[J].天然气与石油,2010,28(4):5-7.
[7]苑伟民.摩阻系数方程对比研究[J].天然气与石油,2014,32(6):21-24.
GERGEquation ofGas Friction Factor and Its Explicit Formula
YUAN Weimin
GuangxiLiquefied NaturalGas Engineering Project Management Department of Sinopec Gas Company,Beihai536000,China
A crucial issue in predicting flow in gas pipelines is the proper choice of the formula for calculating the transmission factor λ.Colebrook-White equation is not a universal formula suitable for all flow states.A new equation for calculating the transmission factor is introduced,that is GERG equation which has a wider application scope and is able to substitute Colebrook-White equation and Zegarola equation in certain cases.Based on the known data and adjustment of the equation parameters,GERG equation can offer the calculation results that the all typical equations of transmission factor can offer.But GERG equation is the implicit equation of the transmission factor λ and there are some difficulties to solve it.So a new explicit form of the equation is put forward.The explicit formula is calculatively validated and the results show that the new formula is more accurate and takes shorter calculation time,and avoids iterative algorithm of implicit equation.
naturalgas flow;friction factor;GERG equation;explicit formula
10.3969/j.issn.1001-2206.2015.06.003
苑伟民(1981-),男,河南南阳人,工程师,2009年毕业于西南石油大学油气储运工程专业,硕士,现从事油气储运系统仿真与优化研究工作。
2015-05-01

