螺旋叶片轴向排列结构强化管内高黏流体流动特性研究

王 丰， 禹言芳， 吴剑华， 孟辉波

(沈阳化工大学 能源与动力工程学院辽宁省高效化工混合技术重点实验室， 辽宁 沈阳 110142)

螺旋叶片轴向排列结构强化管内高黏流体流动特性研究

王 丰， 禹言芳， 吴剑华， 孟辉波

(沈阳化工大学 能源与动力工程学院辽宁省高效化工混合技术重点实验室， 辽宁 沈阳 110142)

利用计算流体力学方法探讨两种螺旋叶片轴向排列方式对其内部高黏度流体流场的影响，提取两种结构的速度场和压力场分析发现，三维速度场均存在着明显的周期性规律.KSM(Kenics type)叶片对流体的切割分流和改变自旋方向在每个叶片的两端产生的压力降为定值，并且随着雷诺数的增加而线性增加.在两种叶片结构的同侧不同端点位置处存在着压力峰值区域诱导了径向二次流的产生.对速度场和压力场的整体协同性分析发现KSM和SSM对应的协同角随雷诺数的增加而下降，SSM内速度场与压力场的整体协同性优于KSM.

数值模拟； 速度场； 压力场； 场协同； 协同角

化学工业技术的进步促进了现代过程工业的飞速发展，传统的化工设备因其存在着高污染、高能耗的问题已不能满足现代大宗化工生产过程对清洁、高效生产过程的要求[1-2].随着单元操作与化学工艺研究的深入，静态混合技术作为多学科间交叉的新兴技术已经获得更为广阔的发展空间，并且作为一种标准配置的功能单元被应用到更多类型的化工反应和工业生产领域[3-4].静态混合器是一种高效的在线被动式混合设备，能从极大程度上降低化工过程的能耗，提高混合效率，改善生产环境.因此，一度成为国内外学者研究的焦点[4-8].

Kenics型静态混合器是一种典型的静态混合器，在工业上应用的最为广泛.在有关静态混合器的前期研究中，Hobbs等[9-14]课题组以拉格朗日粒子跟踪技术为基础，计算得到庞加莱截面、拉伸率及其概率密度曲线、变异系数等相关参数，定量分析了不同雷诺数，不同长径比下高黏度流体在Kenics型静态混合器内的层流运动的混沌混合特性.孟辉波等[15-17]重点研究了静态混合器内压力、速度的瞬态特性，并将Hilbert-Huang变换引入到静态混合器瞬态压力波动信号的分析中[18-19].Regner等[20-22]分析了Kenics型静态混合器内由于混合元件的特殊结构产生的径向二次流漩涡对压降、条纹剪切速率的影响.Smith和Pongjet[23]研究叶片在不同长径比，不同错位角下左旋-右旋交错排列时的传热特性发现，左旋-右旋交错排列方式的传热效率随长径比的增加而降低，随错位角的增加而增加；平均努塞尔特准数比同旋向的排列方式以及空管分别高出12.8 %～41.9 %和27.3 %～90.5 %.Tajima等[24]研究静态混合器内流体的3种典型运动对二氧化碳水合物形成的影响，发现切割分流对水合物的形成很重要，但不是必要的；改变二次流流向有利于移除二氧化碳表面的水合物膜；而径向混合只有与其他两种运动结合才对水合物的形成起作用.上述对静态混合器的研究成果以Kenics型静态混合器为重点[4]，但对静态混合器内螺旋叶片不同轴向排列方式的研究较少.本文利用数值模拟的方法探讨两种螺旋叶片轴向排列方式对其内部高黏度流体流场的影响，在分析了各自压力场和速度场的基础上，通过协同角的计算，评价压力场与速度场在流场流动过程中的协同效果.

1 场协同理论

场协同的研究最初始于我国学者过增元[25]，他首次通过场协同理论揭示了热量输运的物理机制.通过速度矢量场与热流矢量场之间的配合关系，定量考察了流场和温度场的相互作用关系.韩光泽等[26]将协同角的概念进一步推广，提出了广义场协同的概念.至此，场协同原理开始被广泛地运用于考察压力场、温度场、浓度场、速度场和重力场之间的相互联系[27-29].本文着重分析了静态混合器内速度场与压力场的协同性以考察不同静态混合器的流动性能.

2 数值方法

2.1 物理模型及网格划分

两种螺旋叶片排列方式如图1所示.KSM的混合元件为一系列左旋-右旋交错排列螺旋叶片，首尾相互垂直；SSM的混合元件为一系列右旋叶片，首尾重合分布于管路内.模型的详细尺寸及流体的性质见表1.

图1 螺旋叶片不同排列方式结构

结构尺寸叶片宽度D/mm叶片长度l/mm叶片厚度δ/mm扭转角θ/(°)入口段长度li/mm混合区长度lm/m出口段长度lo/mm流体的物理性质密度，ρ/(kg·m-3)动力黏度，μ/(Pa·s)4060218025720251200500

在Solidworks中生成两种结构的几何模型，导入前处理软件Gambit中进行网格划分，结果如图2所示.

图2 网格划分示意图

在Gambit的网格类型中，结构化网格空间上分布比较规范，可方便地处理边界条件，计算精度高，但适用性不强；非结构化网格的网格单元和节点彼此没有固定规律可循，适用范围广，能够灵活方便的模拟绕复杂外形的流动.考虑到本次模拟模型的螺旋结构，对每个模型生成整体化非结构网格.两种模型对应的非结构化网格数目分别为1 283 283和1 282 046，经网格质量检查，所有网格的等尺寸斜率均不超过0.77，可见网格质量较好.

2.2 控制方程及边界条件

在稳态流动中，流体的密度不随时间发生变化，因此质量守恒方程可简化为：

▽u=0

(1)

动量守恒方程为：

div(μgradu)-▽p+Si

(2)

其中：ρ为流体密度；μ表示动力黏度；u是速度矢量；▽p为压力梯度；Si是广义源项，Sx=Fx+sx，Sy=Fy+sy，Sz=Fz+sz，Fx，Fy，Fz是流体微元体上的力，sx，sy，sz是小量，对于黏性为常数的不可压缩流体sx=sy=sz=0.

为解决空管中流体经过一定管长的自由流动才能达到充分发展阶段的问题，以往关于静态混合器的数值模拟通常预留了长度为两倍混合器直径的入口段[10,30].考虑到入口流体速度分布对静态混合器流场的影响[31]，同时为减少网格数目和提高计算效率，本次模拟通过UDF(User Defined Function)自定义函数定义抛物面速度入口(Re=0.1～100).流体出口定义为自由流动出口，压力参考点选为出口截面的中心处，压力和速度耦合采用SIMPLEC算法，压力离散采用Standard格式，动量离散采用二阶迎风格式.

2.3 模型有效性验证

计算流体力学中，压力场较速度场、浓度场对扰动更为敏感[32].因此速度场的数值计算结果的精度依赖于压力场数值计算结果的准确性.而对于静态混合器内压力降的表征，多数以同等尺寸空管的流动阻力Δp0为基准，计算压力降因子Z=Δp/Δp0.长径比Ar为1.5含有6个混合元件的KSM内数值模拟所得的压力降数值随雷诺数的变化趋势与文献中的计算结果一致性很好[33]，从一定程度上说明数值模拟结果的合理性和精确度.

3 结果与讨论

3.1 速度场和压力场

为深入剖析静态混合器内部流场的周期性特点，提取轴截面内(x=R/2，y=R/2)处的三维速度进行分析，结果如图3所示.

图3 三维速度分布

图3给出了流场中该位置点上3个方向的速度沿轴向的变化规律.总体看来，两种混合器内部的流场沿轴向呈现出规律明显的周期性特征.由于KSM中螺旋元件左旋-右旋交替排列，因此其径向速度的周期性为2个螺旋叶片长度.由于相邻元件旋向相反，x，y方向上的速度均有正有负.而SSM内部元件结构相同，因此径向速度周期为1个混合元件，并且径向不会发生二次流方向的翻转.从图3可以观察到，KSM整体速度的波动幅值约为SSM波动幅度的2倍.二者的轴向速度全部为正，说明轴向方向上不会发生混合物的返混.

图4展示了两种结构静态混合器内总压力降Δp随Re的变化规律.从图4可以看出：随着Re的增加，由于流动的不稳定性增加，不同叶片组件的压力降也相应增加，即混合器内的流体阻力逐渐增加.由于缺少了切割分流以及改变自旋方向的作用致使SSM内部的阻力始终低于KSM.图5为Re=0.1时，混合器内部压力降随轴向位置的变化，当流体流经相同长度的管路时，KSM的压力降高于SSM，并且随着叶片个数的增加，两者之间的差别越来越大.经计算发现，当不考虑进出口影响时(排出第一个元件和最后一个元件)，每个KSM叶片两端的压力降与每个SSM叶片两端的压力降都为定值.并且每个KSM叶片两端面的压力降均比相应位置的SSM叶片高出12 %，说明单个叶片长度内叶片切割分流与改变自旋作用产生的压力降为定值.

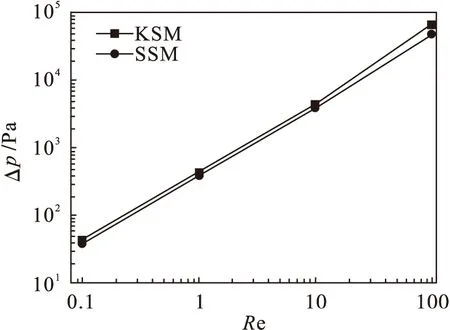
图4 压力降随Re变化规律

为衡量切割分流及改变自旋引起的压力降随雷诺数的变化，引入一个新的参数Cp，定义如下：

(3)

Cp=0.19Re+10.65

(4)

从公式(4)中可以看出：随着Re提高，Cp指数呈线性规律增加，表明混合器内由于螺旋叶片对流体的切割分流与改变旋向作用所产生的阻力随Re的增加而线性增加.

图5 压力降随轴向位置的变化

图6 Cp值随Re变化规律

3.2 速度场与压力场的协同

选取第6个元件中间截面(z=355 mm)以及第6个和第7个元件之间的截面(z=385 mm)进行分析，提取截面上的压强和速度，其分布如图7所示，其中矢量图表示径向二次流的分布，矢量长度表示速度大小，云图表示压强分布.从图7可以看出：在叶片同一侧靠近壁面处会形成一个高压区和一个低压区，而叶片对应的另一侧分别为低压区和高压区.在KSM的元件过渡处，由于相邻元件旋转方向不同，压力峰值区的位置发生了偏转和拉伸.压力梯度促进了流体从高压区向低压区的流动，速度矢量穿过压力等值线.由于轴截面内压力梯度的存在，使得截面内部出现了比较明显的二次流，二次流的产生使同一截面内不同径向位置的流体得以相互掺混，可以提高流体间的传质效果.压力场与速度场的协同效果可以通过协同角定量地进行分析.

图7 不同横截面的压力场和速度场分布

3.3 协同角的计算

对于无外力做功，不可压缩理想流体而言，流体流动的动能方程可以简化为[34]：

(5)

该方程表示单位时间内作用在流体微团上各种力做功之间的关系，其中方程右边第二项是单位时间内压力对单位质量流体所做的功，可记为：

Np=-u·▽p=-|u|·|▽p|·cosθ

(6)

式中，θ为速度和压力梯度之间的夹角，cosθ越趋向于-1，即θ越大，速度与压力梯度的协同性越好，压力梯度的做功能力越强.

为了对整体区域的压力场和速度场的协同程度进行评价，引入积分中值平均角，其计算方法如下：

(7)

式中：ui，Vi，θi分别表示每个控制单元的速度，体积和协同角；gradpi表示控制单元的压力梯度.积分中值平均角的物理意义可解释为，当全场局部协同角都取得该数值时，计算得到的压力场做功总和等于实际情况压力场所做的功.

图8为两种螺旋结构内部速度场与压力场协同角随雷诺数的变化.从图8可以看出：两种协同角的数值均随着雷诺数的增加而下降，SSM对应的协同角整体位于KSM对应的协同角之上.说明SSM内部速度场与压力场的协同效果好于KSM，流体在流经SSM时，损失的压力降大部分用于推动流体做功，增加了流体的径向和轴向速度.

图8 协同角随Re的变化

4 结 论

(1) 基于Kenics静态混合器结构特点，提出一种新的螺旋式结构静态混合器.发现KSM径向速度周期为SSM径向速度周期的2倍；轴向速度周期相同，KSM速度波动幅值是SSM的2倍.

(2) 两种结构的压力降随雷诺数的增加而呈现指数规律上升，Re越大，两种结构产生的压力降差别越大；在给定Re下，由切割分流与改变自旋作用在每个叶片两端产生的压力降为定值，并且随Re的增加而线性增加，与叶片个数无关.

(3) 两种结构的速度场与压力场的积分中值协同角随Re的增加而下降，SSM内速度场与压力场整体的协同性好于KSM.

[1] Jin Y,Cheng Y.Chemical Engineering in China:Past,Present and Future[J].AIChE Journal,2011,57(3):552-560.

[2] 高春坡，李亚芳，赵中博.我国化工过程强化技术理论与应用研究进展[J].化工进展,2011,30(1):1-15.

[3] 骆培成,程易,汪展文,等.液-液快速混合设备研究进展[J].化工进展,2005,24(12):1319-1326.

[4] 禹言芳,王丰,孟辉波,等.旋流静态混合器内瞬态流动特性的研究进展[J].化工进展,2013,32(2):255-262.

[5] Tajima H,Nagata T,Abe Y,et al.HFC-134a Hydrate Formation Kinetics during Continuous Gas Hydrate Formation with a Kenics Static Mixer for Gas Separation[J].Industrial and Engineering Chemistry Research,2010,49(5):2525-2532.

[6] Tajima H,Yamasaki A,Kiyono F,et al.Size Distribution of CO2Drops in a Static Mixer for Ocean Disposal[J].AIChE Journal,2006,52(8):2991-2996.

[7] Kumar V,Shirke V,Nigam K D P.Performance of Kenics Static Mixer Over a Wide Range of Reynolds Number[J].Chemical Engineering Journal,2008,139(2):284-295.

[8] Thakur R K,Vial Ch,Nigam K D P,et al.Static Mixers in the Process Industries—A Review[J].Chemical Engineering Research and Design,2003,81(7):787-826.

[9] Hobbs D M,Alvarez M M,Muzzio F J.Mixing in Globally Chaotic Flows:A Self-similar Process[J].Fractals,1997,5(3):395-425.

[10]Hobbs D M,Muzzio F J.The Kenics Static Mixer:A Three-dimensional Chaotic Flow[J].Chemical Engineering Journal,1997,67(3):153-166.

[11]Hobbs D M,Swanson P D,Muzzio F J.Numerical Characterization of Low Reynolds Number Flow in the Kenics Static Mixer[J].Chemical Engineering Science,1998,53(8):1565-1584.

[12]Hobbs D M,Muzzio F J.Effects of Injection Location,Flow Ratio and Geometry on Kenics Static Mixer Performance[J].AIChE Journal,1997,43(12):3121-3132.

[13]Hobbs D M,Muzzio F J.Optimization of a Static Mixer Using Dynamical System Techniques[J].Chemical Engineering Science,1998,53(18):3199-3213.

[14]Hobbs D M,Muzzio F J.Reynolds Number Effects on Laminar Mixing in the Kenics Static Mixer[J].Chemical Engineering Journal,1998,70(2):93-104.

[15]孟辉波,高艳丽,禹言芳,等.旋流静态混合器内脉动壁压符号时间序列复杂度分析[J].实验流体力学,2011,25(5):30-34.

[16]吴剑华,孟辉波,高艳丽,等.旋流型静态混合器内瞬态速度时间序列多尺度符号化分析[J].应用基础与工程科学学报,2011,19(5):799-809.

[17]吴剑华,孟辉波,禹言芳,等.SK型静态混合器壁压脉动信号的多尺度多分形特性[J].化工学报,2009,60(8):1965-1973.

[18]Meng H B,Liu Z Q,Yu Y F,et al.Time-frequency Analysis of Hilbert Spectrum of Pressure Fluctuation Time Series in Kenics Static Mixer Based on Empirical Mode Decomposition[J].Brazilian Journal of Chemical Engineering,2012,29(1):167-182.

[19]Meng H B,Liu Z Q,Yu Y F,et al.Intrinsic Mode Entropy Analysis of Tube-wall Pressure Fluctuation Signals in the Kenics Static Mixer[J].International Journal of Chemical Reactor Engineering,2011,9(1):1-19.

[20]Regner M,Östergren K,Trägårdh C.Effects of Geometry and Flow Rate on Secondary Flow and the Mixing Process in Static Mixers-A Numerical Study[J].Chemical Engineering Science,2006,61(18):6133-6141.

[21]Regner M,Östergren K,Trägårdh C.Influence of Viscosity Ratio on the Mixing Process in a Static Mixer:Numerical Study[J].Industrial and Engineering Chemistry Research,2008,47(9):3030-3036.

[22]Regner M,Östergren K,Trägårdh C.An Improved Numerical Method of Calculating the Striation Thinning in Static Mixers[J].Computers and Chemical Engineering,2005,30(2):376-380.

[23]Eiamsa-ard S,Promvonge P.Performance Assessment in a Heat Exchanger Tube with Alternate Clockwise and Counter-clockwise Twisted-tape Inserts[J].International Journal of Heat and Mass Transfer,2010,53(7/8):1364-1372.

[24]Tajima H,Yamasaki A,Kiyono F.Effects of Mixing Functions of Static Mixers on the Formation of CO2Hydrate from the Two-phase Flow of Liquid CO2and Water[J].Energy Fuels,2005,19(6):2364-2370.

[25]Guo Z Y,Li D Y,Wang B X.A Novel Concept for Convective Heat Transfer Enhancement[J].International Journal of Heat and Mass Transfer,1998,41(14):2221-2225.

[26]韩光泽,华贲,魏耀东.传递过程强化的新途径——场协同[J].自然杂志,2002,24(5):273-277.

[27]Chen Q,Meng J A.Field Synergy Analysis and Optimization of the Convective Mass Transfer in Photocatalytic Oxidation Reactors[J].International Journal of Heat and Mass Transfer,2008,51(11/12):2863-2870.

[28]陈迁乔,钟秦.螺旋管内对流传质场协同强化模拟[J].化工学报,2012,63(12):3764-3770.

[29]周俊杰,陶文铨,王定标.场协同原理评价指标的定性分析和定量讨论[J].郑州大学学报：工学版,2006,27(2):45-47.

[30]Saatdjian E,Rodrigo A J S,Mota J P B.A Study of Mixing by Chaotic Advection in Two Three-dimensional Open Flows[J].Chemical Engineering Science,2012,81:179-190.

[31]黄娜,吴剑华,张春梅,等.边界条件对SK型静态混合器层流流场的影响[J].北京化工大学学报：自然科学版,2008,5(4):90-94.

[32]Rauline D,Tanguy P A,Le Blévec J M,et al.Numerical Investigation of the Performance of Several Static Mixers[J].The Canadian Journal of Chemical Engineering,1998,76(3):527-535.

[33]Meng H B,Wang F,Yu Y F,et al.A Numerical Study of Mixing Performance of High-viscosity Fluid in Novel Static Mixers with Multitwisted Leaves[J].Industrial and Engineering Chemistry Research,2014,53(10):4084-4095.

[34]祥麟,胡庆康,景思睿.高等流体力学[M].西安:西安交通大学出版社,1989:97.

Analysis of Flow Characteristics of High Viscosity Fluid in Tube with Different Twist Blade Arrangements

WANG Feng, YU Yan-fang, WU Jian-hua, MENG Hui-bo

(Shenyang University of Chemical Technology, Shenyang 110142, China)

The flow fields of high viscosity fluid in the static mixers with two arrangements of twist leaves were studied using CFD method.The analysis of velocity and pressure shows that the three-dimensional velocity fields of two structures are periodic.The pressure drop of each leaf caused by flow division and flow reversal is constant and increases linearly with increasingRe.There exist peak values of pressure in the different ends of the same side in leaves.The pressure gradient is beneficial to the formation of secondary flow.The research on the global synergy of velocity and pressure fields reveals that the field synergy angles of two structures decrease with increasingRe.The global synergy of velocity and pressure fields in SSM is better than that in KSM.

numerical simulation; velocity field; pressure field; field synergy; synergy angle

2013-12-20

国家自然科学基金(21106086，21306115，21476142)；辽宁省高等学校优秀人才支持计划(LR2015051)；辽宁省教育厅科研项目计划(L2013164)；辽宁省博士启动资金项目(20131090)

王丰(1987-)，男，山东烟台人，硕士研究生在读，国家奖学金获得者，主要从事化工过程强化的研究.

孟辉波(1981-)，男，辽宁沈阳人，副教授，博士，主要从事静态混合、射流流动与混合的研究.

2095-2198(2015)04-0329-07

10.3969/j.issn.2095-2198.2015.04.008

TQ051.7

A