弹性介质中输流碳纳米管的热弹性振动分析

梁 峰, 田 健, 金 莹, 包日东

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

弹性介质中输流碳纳米管的热弹性振动分析

梁 峰, 田 健, 金 莹, 包日东

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

应用非局部黏弹性欧拉梁模型研究弹性介质中输流碳纳米管在不同温度环境中的热弹性振动和稳定性问题.对于包含有小尺度项和热效应项的控制方程，利用复模态法计算系统的固有频率和临界流速，并用平均法得到脉动内流作用时管道参数振动稳定性边界的解析表达式，讨论了非局部效应、热效应及弹性介质对系统稳定性的影响.结果表明：高温环境(高于室温)中纳米管系统的固有频率、临界流速和参数共振稳定性都比低温环境(低于或等于室温)中低，而温度变化量、非局部效应和弹性介质等在不同温度环境中对纳米管系统的影响也不同.

输流碳纳米管； 热弹性振动； 温度环境； 非局部效应； 弹性介质

纳米材料作为一种高性能优质材料，已经在国防工业、农业及民生各个领域得到了广泛应用，而1991年才被发现的碳纳米管[1]，被看作是纳米材料中最重要的成员.研究表明，碳纳米管具有十分优异的力学、电磁学和化学性能，其杨氏模量极高，可达1.0 TPa，强度是钢的100倍，是已知材料中最高的，但密度仅为钢的1/6，无论是强度还是韧性都远远优于任何已知纤维材料.碳纳米管作为复合材料的增强体，表现出了良好的强度、弹性、抗疲劳性，同时还具有耐强酸、强碱，在空气中973 K以下基本不被氧化等优良性质.目前，碳纳米管已经在物理、化学、生物、电子和材料等领域得到了广泛的研究和应用，对碳纳米管的力学研究已在国际上形成了研究热点[2-5].

作为一种典型的小尺度高流速流固耦合系统，输流碳纳米管常常会表现出极其丰富的动力学现象.Yoon等[6]和 Reddy等[7]应用单弹性梁模型研究了输流碳纳米管的自由振动和结构不稳定性，证明了纳米管道内部的高速流体对管道的振动频率和振幅衰减率有明显影响；基于此项研究，Wang等[8]应用多弹性梁模型研究了输流双壁碳纳米管的固有频率和屈曲失稳特性，发现其共振频率取决于流体流速，当流速达到一定值时，碳纳米管就会发生屈曲失稳；Yan等[9-10]的研究结果也证明了内部高速流体和层间的范德华力是引起输流多壁碳纳米管失稳的重要原因.总之，研究碳纳米管固体力学行为的文献很多，而关于碳纳米管内流体流动问题的研究则较少，有关流固耦合下，尤其是脉动内流作用下，碳纳米管的动力学行为以及振动稳定性方面的研究报道更少.随着纳米科技的发展，输流纳米结构在工业工程、生物、医疗等领域的应用日益广泛，其力学问题也应该得到广泛关注.这也是本文研究的意义所在.

碳纳米管的纳米级壁厚使得其对温度具有相当的敏感性.而输流碳纳米管又常常工作在各种温度环境中，因此，深入研究热效应对输流碳纳米管动力学特性的影响具有重要意义.目前，有部分文献对输送定常流碳纳米管的热弹性振动问题进行了研究.其中，Chang等[11]研究了热效应对输流单壁碳纳米管屈曲稳定性的影响；Zhen等[12]研究了生物软组织中输流双壁碳纳米管的热弹性振动问题；Ansari等[13]则对弹性介质中输流单壁碳纳米管在考虑热效应时的非线性振动问题进行了研究.实际上，不论是纳米管还是大尺度管道，其内部流体动力源大多为脉动形式，因此，绝对的定常内流只是一种理想情况，而绝大多数管内流态都是脉动的[14].但目前尚未发现有对脉动流作用下碳纳米管的热弹性参数振动问题开展的研究.鉴于此，本文应用非局部黏弹性欧拉梁模型研究弹性介质(模拟周围生物组织液、化学溶剂等环境介质)中输送脉动流的碳纳米管在不同温度环境中的热弹性振动问题，重点分析热效应、非局部效应及弹性介质参数对系统固有频率、临界流速和参数振动稳定性的影响.所得结论可为工程输流纳米机械的设计分析提供一定的理论基础.

1 运动微分方程

图1所示为弹性介质中两端固定输流碳纳米管的力学模型.假定管道只发生横向面内振动y(x,t)，管道轴线沿x轴，t为时间变量，K为弹性介质参数.则由非局部弹性和热弹性理论，并根据管道和流体单元的力和力矩平衡，可以得到温度环境中输流碳纳米管的横向振动微分方程为[11]

(1)

式中，c、E、I、L、m分别为管道的Kelvin-Voigt型黏弹性系数、杨氏模量、截面惯性矩、长度、单位长度的质量；Nt为由热效应引起的轴向常力；e0a为表征纳米尺度效应的非局部参数;M为管内流体单位长度的质量；U为流速.若Nt=e0a=0，则方程(1)将退化为经典的欧拉型方程.

根据热弹性力学理论，轴向力Nt可表示为[11,15]

(2)

式中，v为管材泊松比，αx为管道轴向热膨胀系数，ΔT为相对室温的温度变化量.

引入无量纲变量和参数

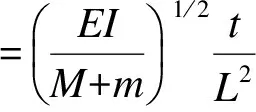
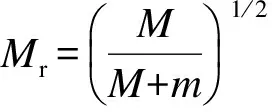
(3)

则方程(1)可转化为如下无量纲形式

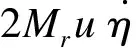
(4)

式中，()′和(·)分别表示∂()/∂ξ和∂()/∂τ.

图1 弹性介质中两端固定输流碳纳米管模型

2 固有频率和临界流速

ηn(ξ，τ)=φn(ξ)eiωnτ

(5)

式中，ωn和φn分别为第n阶固有频率和相应的振型函数.本文研究小阻尼情况，即黏弹性系数α≤1.将式(5)代入方程(4)中可得

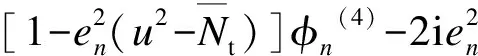
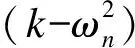
(6)

两端固定的边界条件为

φn(0)=φn(1)=0，φn′(0)=φn′(1)=0

(7)

方程(6)是个4阶齐次常微分方程，设其解为

φn(ξ)=C1n(eid1nξ+C2neid2nξ+

C3neid3nξ+C4neid4nξ)

(8)

式中，djn(j=1,2,3,4)满足下面的特征方程

(9)

将式(7)代入式(8)中可得到关于C1n～C4n的线性方程组

(10)

上式若存在非零解,则系数矩阵行列式为零，由此条件及式(8)～(10)即可解出ωn和φn.

下面通过数值算例来分析温度环境对输流碳纳米管固有频率和临界流速的影响.算例中的碳纳米管采用以下几何和物理参数[11,15]：纳米管密度ρt=2.3 g/cm3，外半径Ro=3.5 nm，壁厚h=0.34 nm，长径比L/(2Ro)=100，E=1 TPa，v=0.3，e0a=70 nm，内流密度ρw=1 g/cm3，弹性介质参数K=0.01 MPa.由Jiang等[16]的研究可知:纳米管的热膨胀系数在低温环境(低于或等于室温)中为负值，而在高温环境(高于室温)中为正值.本文低温环境中取αx=-1.6×10-6K-1，高温环境中取αx=1.1×10-6K-1[17].

图2给出了高温和低温环境中，不同温度变化量下系统第一阶固有频率ω1(最低共振频率)随流速的变化.图中，当u=0时，ω1为不同温度变化量下空管的第一阶固有频率.而随着流速的增大，固有频率逐渐降低直至为零，此时系统将发生屈曲失稳(管道屈曲变形)，而此时的流速即为临界流速ucr.从图2中可以看出：在不同的温度环境中，纳米管系统固有频率和临界流速的变化规律是截然不同的.在低温环境中，考虑热效应时其固有频率(对于一个给定的流速值)和临界流速要比不考虑热效应(ΔT=0)时有所增大.而且，随着温度变化量的增加，固有频率和临界流速都会增大；而在高温环境中，以上变化规律正好相反，尤其是在相同的温度变化量下，高温环境中的纳米管临界流速要比低温环境中低，说明系统在高温环境中的屈曲稳定性要比低温环境中弱.输流碳纳米管的这种对周围温度环境的依赖性是其重要特性之一，应引起研发和设计人员的重视.

图2 两种温度环境中不同温度变化量ΔT下输流碳纳米管第一阶固有频率ω1随流速u的变化

3 脉动内流作用时的动态稳定性

考虑脉动内流情况，设方程(4)中受扰流速为

u=u0[1+μcos(ωτ)]

(11)

式中，u0为平均流速，ω和μ分别为无量纲脉动频率和幅值(μ≤1).将式(11)代入方程(4)后用两振型Galerkin展开式

(12)

进行离散化处理，式中，qi(τ)为广义坐标，Ψi(ξ)为两端固定梁的振型函数.则由振型的正交性并经适当变换后可得一阶微分方程组

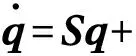
μB2qcos(ωτ)-αB3q

(13)

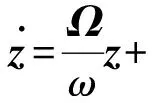
(14)

z2i-1=aicosβi,z2i=aisinβi,i=1,2

(15)

当n1=1/2时，系统平均化方程为：

(16)

(17)

若系统不满足上式条件，则将发生第一阶主参数共振.

仍选取上节数值算例中的碳纳米管来分析其在脉动内流作用时的参数振动稳定性，其黏弹性系数和管内平均流速分别取为：c=2.5×10-10s，U=240 m/s.图3给出了不同温度环境中由式(17)确定的ω-μ平面上第一阶主参数共振边界曲线随温度变化量的变化.其中曲线内部为发生参数共振区域，外部为稳定区域.由图3可见:不同温度环境中温度变化对稳定性区域的影响是截然不同的.首先，在高温环境中，相比不考虑热效应(ΔT=0 K)的情况，考虑热效应时管道共振区域向低频方向移动，表明共振频率降低，而且共振区域的面积明显增大，说明纳米管发生参数共振的频率范围增大，也即稳定性降低；而在低温环境中刚好相反，考虑热效应时不仅共振频率升高，而且系统稳定性也比不考虑热效应时更高.其次，相比低温环境，高温环境中相同参数下(如：ΔT=10 K或20 K)纳米管的共振频率更低，共振区域面积也更大，说明纳米管在高温环境中的稳定性要比低温环境中弱.此外，随着温度变化量ΔT的增加，在高温环境中，共振频率逐渐降低，而且共振区域也逐渐增大，说明管道稳定性降低；而在低温环境中，不仅共振频率升高，而且共振区域也减小，说明管道稳定性增强.可见，周围温度环境以及温度变化都对输流碳纳米管的参数共振稳定性有很重要的影响.

图3 两种温度环境中输流碳纳米管稳定性区域随温度变化量ΔT的变化

图4分析了不同温度环境中纳米管稳定性区域随非局部参数的变化(ΔT=20 K).图4中除了再次反映出相同参数下纳米管在高温环境中的稳定性要比低温环境中弱外，还可以发现，无论在哪种温度环境中，增大非局部参数值都会降低共振频率，还会增大共振区域，使管道稳定性降低.但是相比之下，改变相同的非局部参数值在高温环境中对管道稳定性的影响程度远大于在低温环境中.图5则分析了不同温度环境中纳米管稳定性区域随弹性介质参数的变化(ΔT=20 K).由图5可见:不论在哪种温度环境中，减小介质参数都会降低管道共振频率，同时增大共振区域，降低纳米管稳定性，但是改变相同的介质参数值在高温环境中对管道稳定性的影响程度远大于在低温环境中.图4和图5的结论表明:系统参数对管道稳定性的影响程度也会随着温度环境的改变而发生变化，诸如非局部效应和弹性介质等，在高温环境中对纳米管稳定性的影响会比在低温环境中更明显.这也再次体现了输流碳纳米管参数共振稳定性对周围温度环境的依赖性.

综上可知，输流碳纳米管所处的温度环境对其稳定性有重要的影响.而综合前面的分析可知，高温环境对纳米管的稳定性是相当不利的.这是输流碳纳米管一个很重要的特性.

图4 两种温度环境中输流碳纳米管稳定性区域随非局部参数e0a的变化

图5 两种温度环境中输流碳纳米管稳定性区域随弹性介质参数K的变化

4 结 论

应用非局部黏弹性欧拉梁模型研究了不同温度环境中输流碳纳米管的热弹性振动和稳定性问题.通过文中分析，可得到以下结论：

(1) 不同的温度环境和温度变化对纳米管的热弹性振动和稳定性有很大影响.

(2) 在高温环境中，纳米管系统的固有频率和屈曲失稳临界流速不仅比无热效应时和低温环境中都要低(屈曲稳定性低)，而且其值还会随着温度变化量的增加而降低，而在低温环境中这些变化规律正好相反.

(3) 纳米管在高温环境中的参数振动稳定性要比低温环境中弱；提高温度变化量，在低温环境中可以增强系统稳定性，而在高温环境中却会降低系统稳定性；增大非局部参数和减小弹性介质参数都会降低系统的稳定性，但在高温环境中这种影响会更明显.

总之，高温环境对输流碳纳米管的振动稳定性是很不利的.因此，在进行输流纳米机械的设计时，应着重考虑实际工况的温度条件，尽量避免长时间高温工作，以保证纳米管安全、稳定地工作，延长纳米管的寿命.

[1] Iijima S.Helical Microtubules of Graphitic Carbon[J].Nature,1991,354(7)：56-58.

[2] Zhang Y Q,Liu G R,Wang J S.Small-scale Effects on Buckling of Multiwalled Carbon Nanotubes under Axial Compression[J].Physical Review B,2004,70(20)：205430.

[3] 陈明君,李洪珠,李旦.碳纳米管力学行为研究的新进展[J].机械工程学报,2005,41(3)：18-24.

[4] Natsuki T,Lei X W,Ni Q Q,et al.Free Vibration Characteristics of Double-walled Carbon Nanotubes Embedded in an Elastic Medium[J].Physics Letters A,2010,374(26)：2670-2674.

[5] Khosrozadeh A,Hajabasi M A.Free Vibration of Embedded Double-walled Carbon Nanotubes Considering Nonlinear Interlayer Van Der Waals Forces[J].Applied Mathematical Modelling,2012,36(3)：997-1007.

[6] Yoon J,Ru C Q,Mioduchowski A.Vibration and Instability of Carbon Nanotubes Conveying Fluid[J].Composites Science and Technology,2005,65(9)：1326-1336.

[7] Reddy C D,Lu C,Rajendran S,et al.Free Vibration Analysis of Fluid-conveying Single-walled Carbon Nanotubes[J].Applied Physics Letters,2007,90(13)：133122.

[8] Wang L,Ni Q,Li M.Buckling Instability of Double-wall Carbon Nanotubes Conveying Fluid[J].Computational Materials Science,2008,44(2)：821-825.

[9] Yan Y,Wang W Q,Zhang L X.Dynamical Behaviors of Fluid-conveyed Multi-walled Carbon Nanotubes[J].Applied Mathematical Modelling,2009,33(3)：1430-1440.

[10]Yan Y,He X Q,Zhang L X,et al.Dynamic Behavior of Triple-walled Carbon Nanotubes Conveying Fluid[J].Journal of Sound and Vibration,2009,319(3/5)：1003-1018.

[11]Chang T P.Thermal-mechanical Vibration and Instability of a Fluid-conveying Single-walled Carbon Nanotube Embedded in an Elastic Medium Based on Nonlocal Elasticity Theory[J].Applied Mathematical Modelling,2012,36(5)：1964-1973.

[12]Zhen Y X,Fang B,Tang Y.Thermal-mechanical Vibration and Instability Analysis of Fluid-conveying Double Walled Carbon Nanotubes Embedded in Visco-elastic Medium[J].Physica E,2011,44(2)：379-385.

[13]Ansari R,Hemmatnezhad M,Rezapour J.The Thermal Effect on Nonlinear Oscillations of Carbon Nanotubes with Arbitrary Boundary Conditions[J].Current Applied Physics,2011,11(3)：692-697.

[14]梁峰,杨晓东,闻邦椿.基于增量谐波平衡法的两端固定输流管参数共振[J].机械工程学报,2009,45(7)：126-130.

[15]Wang L,Ni Q,Li M,et al.The Thermal Effect on Vibration and Instability of Carbon Nanotubes Conveying Fluid[J].Physica E,2008,40(10)：3179-3182.

[16]Jiang H,Liu B,Hwang Y,et al.Thermal Expansion of Single Wall Carbon Nanotubes[J].Journal of Engineering Materials and Technology,2004,126(3)：265-270.

[17]Yao X H,Han Q.Buckling Analysis of Multiwalled Carbon Nanotubes under Torsional Load Coupling with Temperature Change[J].Journal of Engineering Materials and Technology,2006,128(3)：419-427.

Thermoelastic Vibration of a Fluid-conveying Carbon Nanotube Embedded in Elastic Mediums

LIANG Feng， TIAN Jian， JIN Ying， BAO Ri-dong

(Shenyang University of Chemical Technology, Shenyang 110142, China)

In this paper,a nonlocal viscoelastic Euler-Bernoulli beam model is developed to investigate the thermoelastic vibration and stability of a fluid-conveying carbon nanotube(CNT)embedded in elastic mediums under different temperature environments.The governing equation with small scale and thermal effect terms is solved by the complex mode and the averaging methods and the natural frequency,critical flow velocity and analytical expression of the parametric resonance boundary are obtained.The influences of nonlocal,thermal effects and the elastic mediums on the stability of the system are discussed.The results obtained show that the natural frequency,critical flow velocity and parametric resonance stability of the CNT at high temperatures(higher than room temperature)are all lower than those at low temperatures(lower than or equal to room temperature),and the temperature change,nonlocal effect and elastic mediums have different impacts on the CNT at different temperatures.

fluid-conveying carbon nanotube; thermoelastic vibration; temperature environment; nonlocal effect; elastic medium

2015-01-28

国家自然科学基金项目(51275315)；辽宁省教育厅科学研究一般项目(L2013160)

梁峰(1979-)，男，辽宁抚顺人，讲师，博士，主要从事非线性动力学研究.

2095-2198(2015)03-0257-06

10.3969/j.issn.2095-2198.2015.03.015

O326

A