对比分析三角Pr3+中心在CsCdBr3和GdCl3晶体中的能级分裂
段美玲, 李晋红, 陈 芳
(1.中北大学理学院, 太原 030051; 2.太原科技大学应用科学学院, 太原 030024; 3.中北大学化工与环境学院, 太原 030051)
对比分析三角Pr3+中心在CsCdBr3和GdCl3晶体中的能级分裂
段美玲1, 李晋红2, 陈 芳3
(1.中北大学理学院, 太原 030051; 2.太原科技大学应用科学学院, 太原 030024; 3.中北大学化工与环境学院, 太原 030051)
以Racah的群表示论和Slater的波函数理论为基础,分别建立了4f2组态离子Pr3+在三角晶体场C3v和C3h中的91×91完全能量矩阵,并对Pr3+离子掺杂在卤化物CsCdBr3和GdCl3中的Stark能级做了计算与分析. 结果显示计算值与实验值吻合很好,表明在分析由稀土离子掺杂体系的能级分裂时,完全能量矩阵方法是有效的方法. 此外,将两种具有不同点群对称的体系的能级分裂情况作了比较,结果显示六阶晶体场参量对能级分裂的影响是不能忽略的,而且CsCdBr3:Pr3+和GdCl3:Pr3+将产生不同程度的畸变.
Pr3+; 完全能量矩阵; 能级分裂; 晶体场效应; 畸变
1 引 言
CsCdBr3是典型的AMX3型晶体,其中的(CdBr6)4-团簇是正八面体结构. 当稀土三价离子(RE3+)掺杂其中,RE3+将取代Cd2+离子,并被6个Br-离子包围,形成C3v对称结构. 目前,掺杂晶体CsCdBr3:Pr3+作为发光和激光材料,已经引起人们极大的关注[1-3]. 并且由于Pr3+离子具有良好的分光特性,有望成为制作高分辨率激光光谱仪的备选材料[4, 5]. 鉴此,对CsCdBr3:Pr3+晶体的能级分裂研究有助于理解掺杂晶体性质的物理起因,并能为进一步研究化合物的光学和磁学性质提供有价值的信息. 另外,GdCl3是从镧(La)到钆(Gd)的同构三氯化物的简单晶体,属C3h点群对称. 当Pr3+离子掺杂其中,将直接取代Gd3+离子的位置. GdCl3作为一种顺磁性多层铁磁体,可研制新型微电子器件[6, 7]. 因其相当高的光输出和低衰变时间,常被用作发光闪烁材料;又因钆具有非常大的快中子俘获截面而成为生产中子探测器的备基质材料[8]. 因此分析GdCl3:Pr3+的能级分裂情况对研究复杂化合物具有指导意义.
对于RE离子,晶场作用应描述成二阶、四阶和六阶参量的函数表达式,但是,Chi等人对单电子组态Ce3+离子的晶场作用的研究仅考虑到了四阶参量[9]. 而Stevens等人曾报道了六阶相互作用有时比四阶还重要的结果[10]. 为了给研究多电子组态离子提供完整的信息,我们将在对单电子组态的旋轨和晶场作用进行了全面分析的基础上,得出RE离子电磁结构与晶格结构的依赖关系,进而研究掺杂晶体的能级分裂. 本文在Racah的群表示理论和Slater的波函数理论的基础上[11-13],建立了描述4f2组态离子Pr3+在三角晶场中电磁结构与晶格结构关系的理论方法;计算并分析了Pr3+掺入CsCdBr3和GdCl3晶体中的Stark能级;引用几个晶体场强度量比较了CsCdBr3:Pr3+中的(PrBr6)3-晶格与GdCl3:Pr3+中(PrCl9)6-晶格的晶场效应,并判断了掺杂晶体的畸变.
2 理论模型
2.1 空间基矢
稀土离子组态4fn属于中间耦合态,完备的空间基矢是|J,MJ〉. 它可以写成谱项波函数|L,ML,S,MS〉的线性组合,即:
(1)
而|L,ML,S,MS〉可进一步写成Slater行列式的形式为:
(2)
其中,Ci和Cj叫做Clebsch-Gordon系数.
2.2 自由离子作用
4f2组态离子的有效哈密顿算符可以写成[14]:
i(corr)+CF
(3)
该等式的前三项主要代表自由离子的能量,它们各自的含义已由Newman[14]做了解释. 等式第四项的表达式是:

[αL(L+1)+βG(G2)+γG(R7)]
(4)
其中第一项代表具有相同宇称的组态之间的相互作用,由三个“Trees”参数α,β和γ来描述,分别是李群R3,G2和R7的Casimir算符的本征值[15],表达式如下:
G(R3)=L(L+1)
(5)
式中(u1,u2)和(ω1,ω2,ω3)分别是G2和R7群的不可约表示,用来区分4fn(n≤4)组态的谱项.
2.3 晶场相互作用
当4f2离子处于不同的晶场中,对应的晶场哈密顿量的表达式可以表示如下:
(6)
其中,阶数k以及投影q的值受到4f2离子所在的晶格的点群对称性的限制. 根据晶场哈密顿量的厄米性和时间反演不变性,f电子的阶数k为偶数时为有效值,即k=0,2,4,6. 如果将镧系离子在晶场中的物理信息和几何信息联系在一起,那么几何参数和晶场参数之间存在下列关系:
(7)
(8)
(9)
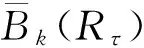
3 理论计算与分析
3.1 CsCdBr3:Pr3+和GdCl3:Pr3+晶场势能
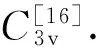
(10)
而具有C3h对称的GdCl3:Pr3+体系的晶场哈密顿量具体为:
(11)
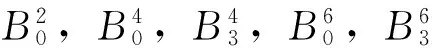
3.2 CsCdBr3:Pr3+和GdCl3:Pr3+能级结构
对于4f2组态离子,Tröster等研究者认为,库仑与旋轨耦合作用对三价离子Pr3+掺杂在三氯化物中的能级分裂的影响比其他作用大得多[17]. 据此,我们建立了Pr3+离子在三角晶场C3v和C3h对称下的完全能量矩阵,并通过对角化计算来分析了两类不同对称性系统的能级分裂. 计算中所用参量列在表1.
表1 计算能级的相互作用参数,单位:cm-1
Table 1 The free ion parameters used to calculate the energy-level of CsCdBr3:Pr3+and GdCl3:Pr3+, all in units of cm-1
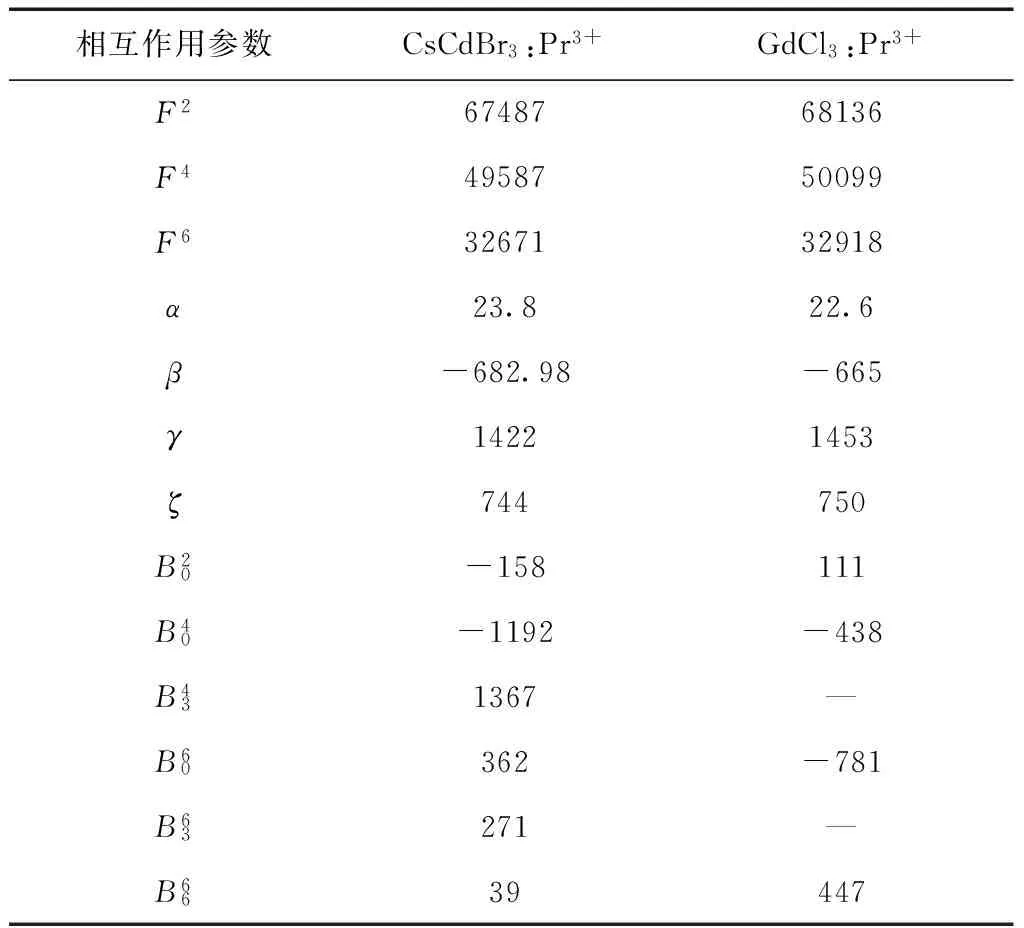
相互作用参数CsCdBr3:Pr3+GdCl3:Pr3+F26748768136F44958750099F63267132918α23.822.6β-682.98-665γ14221453ζ744750B20-158111B40-1192-438B431367—B60362-781B63271—B6639447
利用表1中的能级参数,我们计算得到了在C3v和C3h群操作下,由Pr3+的13个多重态分裂出的61个Stark能级值,见表2-3. 此外表中还列出了CsCdBr3:Pr3+和GdCl3:Pr3+体系能级分裂的实验值[16, 18]、J-多重态、不可约标识及计算与实验值的差值Δ1(Δ1=E(实验)-E(计算)). 由表可见,能级的计算值与实验值吻合很好,相对误差小于0.1%. 可见,对角化完全能量矩阵计算是一种有效地分析被Pr3+离子掺杂体系的能级分裂及研究与能级相关的晶体性质的方法. 另外,由表2-3可知,在不同的群操作下,虽分裂出的能级条数相同,但产生的不可约标识按照群特征标理论是不同的.
3.3 晶场效应
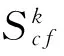
(12)
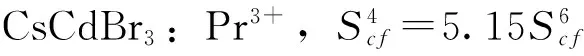
表2 CsCdBr3:Pr3+系统的能级分裂,Δ1是实验值和计算值的差值,单位:cm-1
Table 2 The energy-level splitting of CsCdBr3:Pr3+system, Δ1denotes the difference between the experimental values and the calculated values, all in units of cm-1
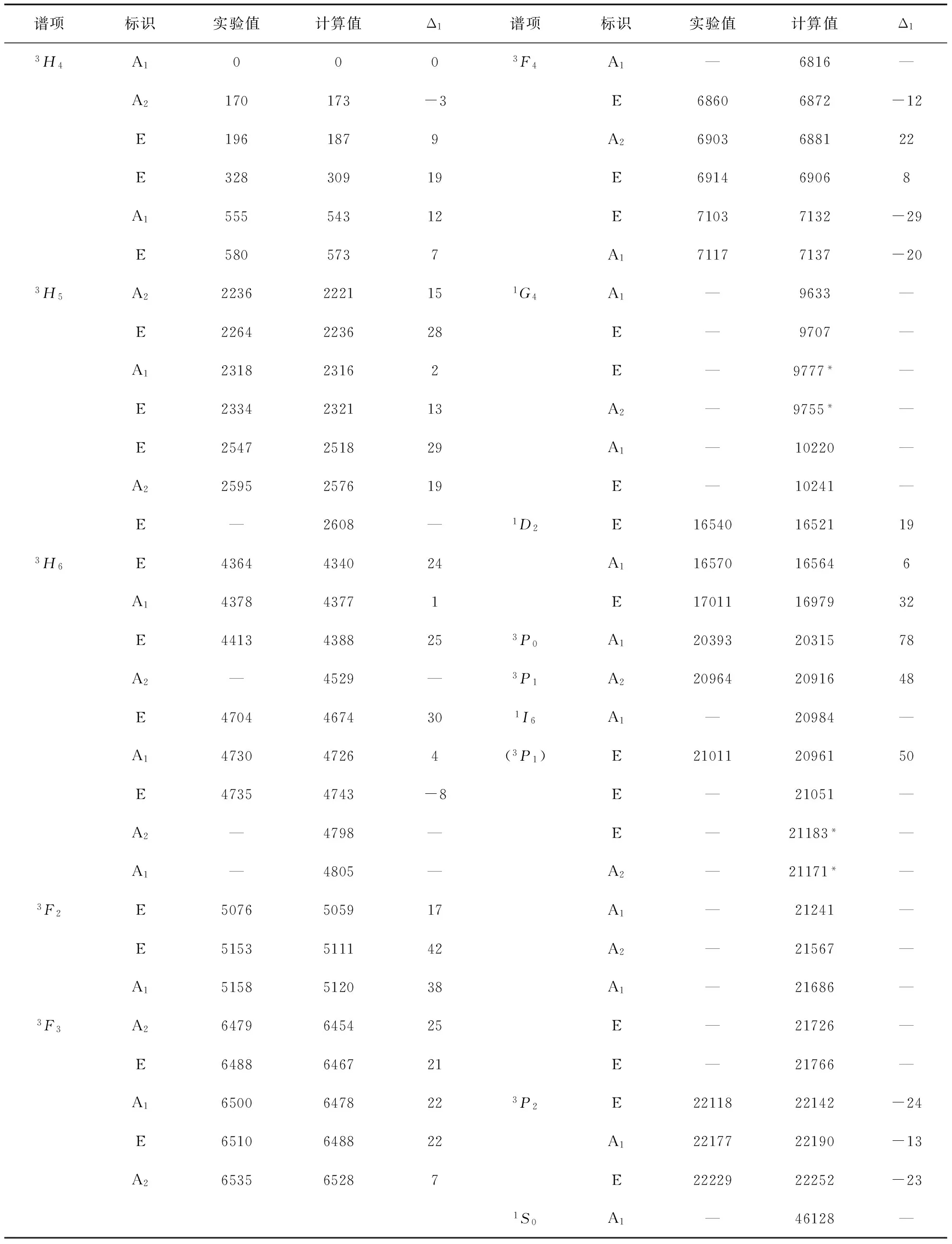
谱项标识实验值计算值Δ1谱项标识实验值计算值Δ13H4A10003F4A1—6816—A2170173-3E68606872-12E1961879A26903688122E32830919E691469068A155554312E71037132-29E5805737A171177137-203H5A222362221151G4A1—9633—E2264223628E—9707—A1231823162E—9777*—E2334232113A2—9755*—E2547251829A1—10220—A22595257619E—10241—E—2608—1D2E1654016521193H6E4364434024A116570165646A1437843771E170111697932E44134388253P0A1203932031578A2—4529—3P1A2209642091648E47044674301I6A1—20984—A1473047264(3P1)E210112096150E47354743-8E—21051—A2—4798—E—21183*—A1—4805—A2—21171*—3F2E5076505917A1—21241—E5153511142A2—21567—A15158512038A1—21686—3F3A26479645425E—21726—E6488646721E—21766—A165006478223P2E2211822142-24E6510648822A12217722190-13A2653565287E2222922252-231S0A1—46128—
“*”表示为保证不可约标识维数的统一,将计算值重新排序;
“( )”表示多重态3P1混在了1I6中
表3 GdCl3:Pr3+系统的能级分裂,Δ1是实验值和计算值的差值,单位:cm-1
Table 3 The energy-level splitting of GdCl3:Pr3+system, Δ1denotes the difference between the experimental values and the calculated values, all in units of cm-1
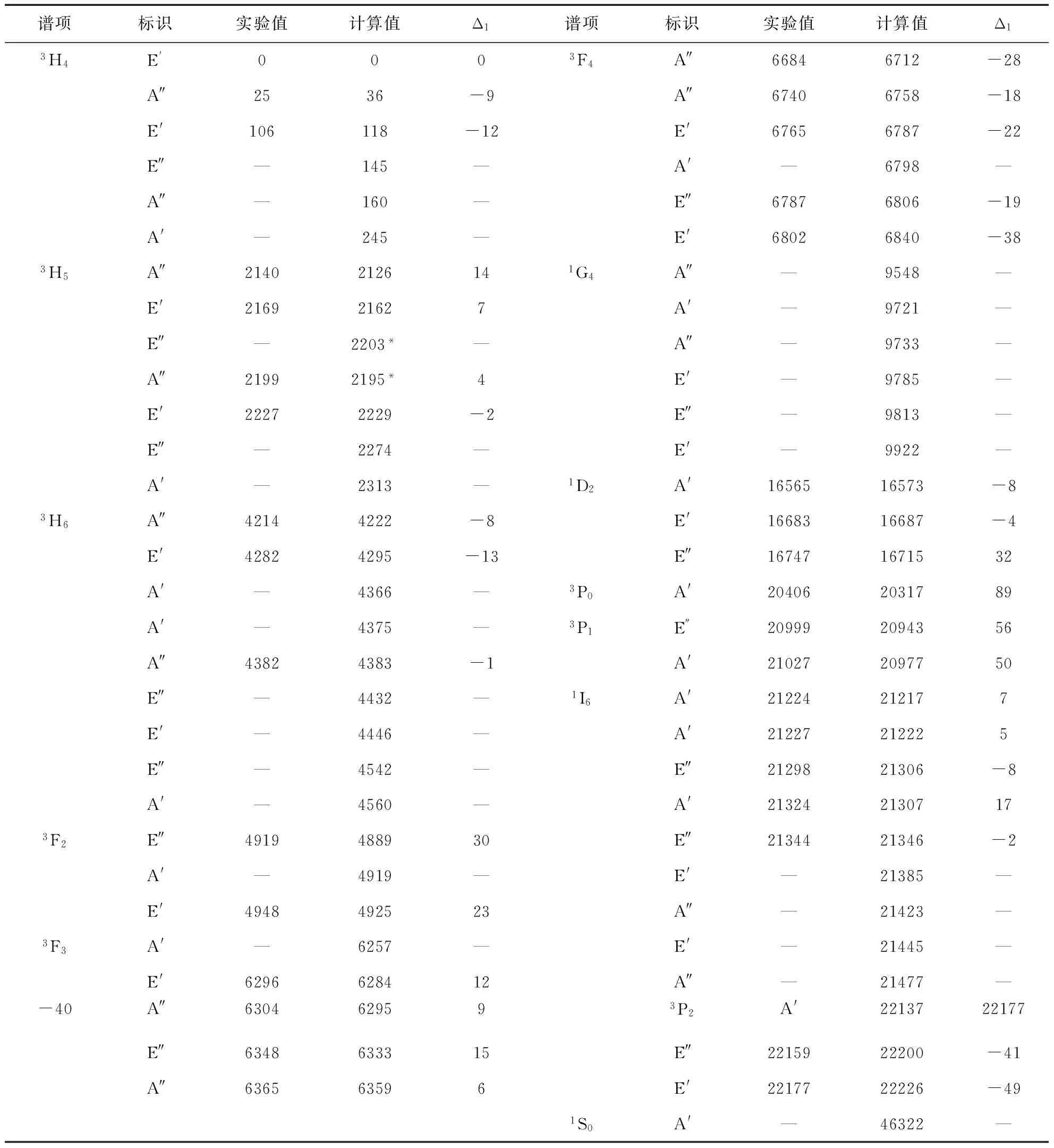
谱项标识实验值计算值Δ1谱项标识实验值计算值Δ13H4E'0003F4A″66846712-28A″2536-9A″67406758-18E'106118-12E'67656787-22E″—145—A'—6798—A″—160—E″67876806-19A'—245—E'68026840-383H5A″21402126141G4A″—9548—E'216921627A'—9721—E″—2203*—A″—9733—A″21992195*4E'—9785—E'22272229-2E″—9813—E″—2274—E'—9922—A'—2313—1D2A'1656516573-83H6A″42144222-8E'1668316687-4E'42824295-13E″167471671532A'—4366—3P0A'204062031789A'—4375—3P1E″209992094356A″43824383-1A'210272097750E″—4432—1I6A'21224212177E'—4446—A'21227212225E″—4542—E″2129821306-8A'—4560—A'2132421307173F2E″4919488930E″2134421346-2A'—4919—E'—21385—E'4948492523A″—21423—3F3A'—6257—E'—21445—E'6296628412A″—21477—A″6304629593P2A'2213722177-40E″6348633315E″2215922200-41A″636563596E'2217722226-491S0A'—46322—
“*”表示为保证不可约标识维数的统一,将计算值重新排序
比Cd2+离子对Br-配体的引力作用强占主导作用;而r(Pr3+) >r(Gd3+)导致与(GdCl9)6-相比,(PrCl9)6-的键长发生了伸长变化.
4 结 论
我们已建立了Pr3+离子在三角晶场C3v和C3h中的完全能量矩阵. 以此为基础,计算了CsCdBr3:Pr3+和GdCl3:Pr3+体系的Stark能级结构,并就两种不同的对称场影响掺杂体系能级分裂的作用做了对比. 得出以下几点结论:
(1)当分析由Pr3+离子掺杂的体系的能级分裂时,对角化完全能量矩阵是一有效的方法;
(2)分析晶场作用对主晶体能级分裂的影响时,必须考虑六阶参量;
(3)与主晶体相比,CsCdBr3:Pr3+将发生压缩变化,而GdCl3:Pr3+将发生伸长变化.
[1] Souza A P, Paz F A A, Freire R O,etal. Synthesis, crystal structure, and modelling of a new tetramer complex of europium [J].J.Phys.Chem. B, 2007, 111: 9228.
[2] Chen X H, Wu T, Wu G,etal. Superconductivity at 43 K in SmFeAsO1-xFx[J].Nature, 2008, 453: 761.
[3] Clarina de la C, Huang Q, Lynn J W,etal. Magnetic order close to superconductivity in the iron-based layered LaO1-xFxFeAs systems [J].Nature, 2008, 453(6): 899.
[4] Chaminade J R, McFarlane R M, Ramaz F,etal. High resolution laser spectroscopy of rare earth doped CsCdBr3[J].J.Lumin., 1991, 48/49: 531.
[5] Shelby R M, Macfarlane R M. Mearsurement of the pseudo-stark effect in Pr3+:LaF3using population hole burning and optical free-induction decay [J].Opt.Commun., 1978, 27: 399.
[6] Jr J M P, Filho R N C. Microscopic theory of dipole-exchange spin waves in magnetic multilayers [J].Eur.Phys.J. B, 2004, 40: 137.
[7] Zassenhaus G M, Woodcraft A L, Reppy J D. A novel method for heat capacity measurements near 2K [J].J.LowTemp.Phys., 1998, 110: 275.
[8] Grippa A Y, Datsko Y N, Zelenskaya O V,etal. Synthesis and scintillation properties of GdCl3:Ce3+(Gd1-xCexCl3, x=0.005-0.08) [J].Radiat.Meas., 2010, 45: 398.
[9] Chi S X, Adroja D T, Guidi T,etal. Crystalline electric field as a probe for long-range antiferromagnetic order and superconducting state of CeFeAsO1-xFx[J].Phys.Rev.Lett., 2008, 101: 217002.
[10] Elliott R J, Stevens K W H. The theory of magnetic resonance experiments on salts of the rare earths [J].Proc.Roy.Soc.Lond. A, 1953, 218: 553.
[11] Racah G. Theory of complex spectra. Ⅰ[J].Phys.Rev., 1942, 61: 186.
[12] Racah G. Theory of complex spectra. Ⅳ [J].Phys.Rev., 1949, 76: 1352.
[13] Slater J C.Quantumtheoryofatomicstructure:Vol. 2 [M]. USA: Mcgraw-Hill Book Company, Inc., 1960: 95.
[14] Newman D J, Betty Ng.Crystalfieldhandbook[M]. UK: Cambridge University Press, 2000: 83.
[15] Budd B R.Operatortechniquesinatomicspectroscopy[M]. New York: Mcgraw-Hill Book Company, Inc., 1963: 11.
[16] Antic-Fidancev E, Lemaitre-Blaise M, Chaminade J,etal. Crystal-field effect in CsCdBr3:Pr3+[J].J.AlloysCompd., 1995, 225: 95.
[17] Tröster Th, Gregorian T, Holzapfel W B. Energy levels of Nd3+and Pr3+inRCl3under pressure [J].Phys.Rev. B, 1993, 48(5): 2960.
[18] Burdick G W, Richardson F S. Application of the correlation-crystal-field delta-function model in analyses of Pr3+(4f2) energy-level structures in crystalline hosts [J].Chem.Phys., 1998, 228: 81.
Comparative analysis of energy levels splitting for the triagonal Pr3+centers in CsCdBr3and GdCl3crystals
DUAN Mei-Ling1, LI Jin-Hong2, CHEN Fang3
(1. School of Science, North University of China, Taiyuan 030051, China; 2. School of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, China; 3. School of Chemical Engineering and Environment, North University of China, Taiyuan 030051, China)
Based upon the combination of Racah’s group-theoretical consideration with Slater’s wavefunctions, the 91×91 complete energy matrix of 4f2configuration ion Pr3+inC3vand C3hcrystal field have been constructed respectively. The calculated Stark energy levels of CsCdBr3:Pr3+and GdCl3:Pr3+present a good agreement with the experimental values, which implies that the complete energy matrix method can be received as a recommendable tool to perform a theoretical analysis to the doped crystal. Besides, the detailed comparison has been performed about the influence of Pr3+ions on the energy levels splitting of the host crystal CsCdBr3and GdCl3doped with Pr3+ions, characterized by different point group symmetry. It indicates that the sixth order crystal field parameters play an indispensable role in splitting the energy levels. Additionally, the two systems will experience different local distortion.
Pr3+; Complete energy matrix; Energy levels splitting; Crystal field effect; Distortion
103969/j.issn.1000-0364.2015.12.030
2014-07-11
国家自然科学基金(11247278,10974138,61405136,61178067,11447219);山西省青年基金(2013021010-4,2012021016)
段美玲(1982—), 女,山西怀仁人,博士,副教授,硕士生导师,主要从事稀磁材料局域特性的理论研究. E-mail: meilingduan@nuc.edu.cn
李晋红.E-mail: jinhongli@live.cn
O562
A
1000-0364(2015)06-1091-06

