球对称铷原子玻色-爱因斯坦凝聚中单极子模的朗道阻尼和频移

彭胜强, 阿孜古丽·热合木提, 马晓栋

(新疆师范大学物理与电子工程学院, 乌鲁木齐 830054)

球对称铷原子玻色-爱因斯坦凝聚中单极子模的朗道阻尼和频移

彭胜强, 阿孜古丽·热合木提, 马晓栋

(新疆师范大学物理与电子工程学院, 乌鲁木齐 830054)

采用含时哈特里-福克-博戈留波夫近似研究球对称铷原子玻色-爱因斯坦凝聚中单极子模的朗道阻尼和频移, 并用现有实验和数值模拟研究的粒子数和囚禁频率参量, 解析计算了阻尼系数和频移大小及其它们的温度依赖. 计算中, 考虑元激发的实际弛豫及其各弛豫间的正交关系以获得阻尼和频移计算公式, 把基态波函数取为高斯分布函数的一级近似以消除三模耦合矩阵元的发散. 我们的计算结果与数值模拟结果和实验结果分别进行直接和间接地对比, 讨论和说明了我们理论方法的合理性.

玻色-爱因斯坦凝聚; 朗道阻尼和频移; 哈特里-福克-博戈留波夫近似; 托马斯-费米近似

1 引 言

玻色-爱因斯坦凝聚(Bose-Einstein condensate, 简称 BEC)中的元激发是量子多体物理研究一个很好的课题[1-16]. 阻尼和频移是元激发的主要特征、也是 BEC 最基本的现象并有大量的观察实验[17-24]. 虽然已有很多关于囚禁 BEC 中集体激发朗道阻尼的理论研究[25-44], 但是阻尼的物理机制还没有得到充分的研究和理解. 尽管频移是阻尼相伴的物理现象, 但只有文献[42]在研究阻尼的同时计算了频移.

集体激发动力学行为的研究在高温高密度下采用二流体理论[25-30]、在低温低密度的情况下采用平均场理论[31-44]. 在平均场理论框架下, 文献[38-42]研究了非均匀囚禁谐振子势阱中的 BEC 集体激发的朗道阻尼. 文献[38-41] 在频率改变的微扰公式中引入洛伦兹分布函数以获得计算阻尼系数的公式, 但是这种方法有一些缺陷, 并且不适用于准一维(quasi-one-dimension, 简称 Q1d)和准二维(quasi-two-dimension, 简称 Q2d)的凝聚体[43，44]. 文献[43，44]在频率改变的微扰公式中考虑元激发的实际弛豫从而用迭代的方法计算阻尼系数. 在文献[43，44]的基础上, 文献[42]又考虑了各弛豫之间的正交关系, 这个问题在 2.3节详细讨论.

由于囚禁在谐振子势中的凝聚体复杂的非均匀特征, 文献[25-38]对朗道阻尼的研究都是数值模拟的. 解析工作仅能通过托马斯-费米近似(Thomas-Fermi-Approximation, 简称 TFA)实现, 而在 TFA 近似下三模耦合矩阵元是发散的. 三模耦合矩阵元利用关于基态波函数的格罗斯-皮塔耶夫斯基(Gross-Pitaevskii, 简称 GP)方程解和关于元激发本征函数集的博格留波夫-德热纳(Bogoliubov-de Gennes, 简称 BdG)方程组解计算出, 对计算阻尼系数非常重要. 文献[39-41]提出了一种改进的 TFA(beyond Thomas-Fermi- Approximation, 简称 bTFA), 通过引入一个决定于变分法的参量q来消除发散而实现了阻尼的解析计算. 这种方法在文献[42]中通过确定q=1进行了改进, 这个问题在 2.4 中详细讨论.

文献[42]研究了雪茄形铷原子凝聚体单极子模的朗道阻尼和频移, 其理论计算结果和文献[20]中的实验结果符合. 本文用同样的方法计算球对称铷原子凝聚体单极子模的朗道阻尼和频移. 理论计算结果将与文献[38]的数值模拟结果与文献[18，20] 的实验结果分别进行直接和间接地对比和分析.

2 关于朗道阻尼和频移的哈特里-福克-博戈留波夫平均场理论

我们采用基于哈特里-福克-博戈留波夫(Hartree-Fock-Bogoliubov, 简称 HFB)平均场近似的解析 BdG 方程本征函数集[14]和频率改变微扰理论公式[31], 在 2.1 和 2.2 节简要介绍.

我们采用文献[42]消除三模耦合矩阵元发散的方法和计算阻尼和频移的公式, 在2.3和2.4节详细讨论.

2.1 BdG 方程的本征函数集

(1)

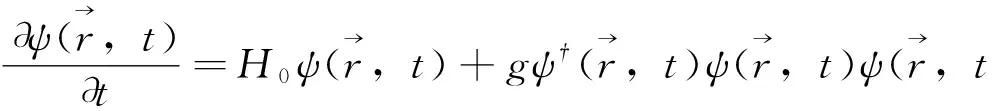
(2)

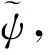
我们采用 HFB 近似[31], 得到凝聚体满足的方程

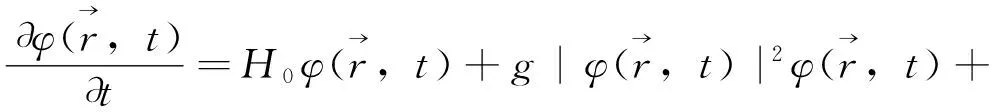
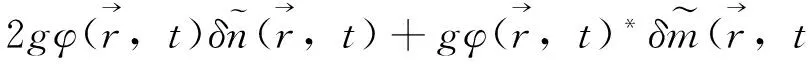
(3)

(4)

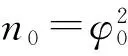
(5)

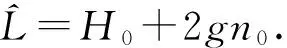
由(3)式还可得到描述凝聚体激发部分的运动方程

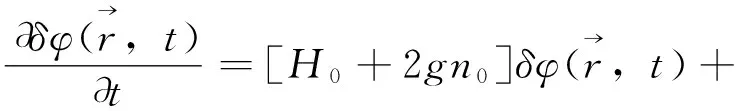
(6)

(7)

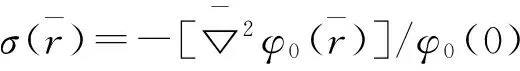
(8)

(7) 式的基态波函数bTFA解为

(9)

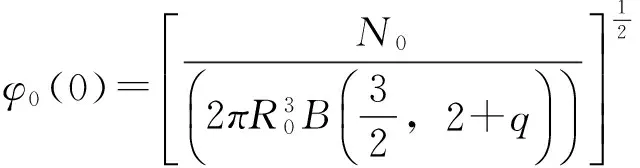
(8) 式的元激发本征函数 bTFA 解为

(10)

其中的参量q将在 2.4 节讨论.

2.2 集体模频率修正公式及其阻尼强度和三模耦合矩阵元表达式

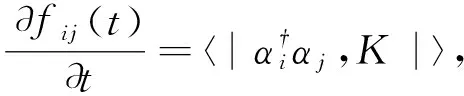
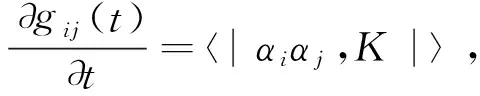
(11)

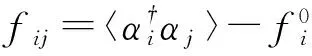
(12)

其中

(13)

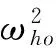
(14)

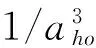
在 (12) 式的右边, 第一项是未修正的集体模频率, 第二项是集体模的频率修正. 满足选择条件ω0+ωi-ωj=0的准粒子跃迁对第二项的贡献非常大. 频率为 ωi的准粒子通过吸收一个频率为 ω0激发模变成了频率为 ωj的准粒子的跃迁是集体模频率改变的朗道机制.

2.3 朗道阻尼和频移的计算公式

由微扰理论推出的 (12) 式, 右边第一项是集体模的零阶频率, 第二项是微扰修正, 第二项在 ω0+ωi-ωj=0 的条件下是发散的.

(15)

而把(15)式的虚部看作是集体模的朗道阻尼系数

(16)

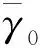
上述方法在文献[42]中进行了如下改进.

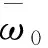
(17)

令 (17) 式的虚部为零, 得到

(18)

和

(19)

(20)

成效三：社会声誉不断提升。2013年1月，学校达到广州市一级学校办学标准，同年，学校的“岭南艺术”特色课程获得广州市特色课程重点立项；2014年，学校成为广州市特色学校，走进了优质学校行列。以前无人问津的薄弱高中得到了学生、家长以及教育同行的高度认可，区教育局、市教育局领导都充分肯定了学校艺术特色办学成效。近年来，武汉、福建、中山、东莞等地以及广州市多所学校师生来校参观交流。学校的美术、音乐联考成绩在省、市内均具有一定的知名度。

(21)

其中, 上述三个弛豫ω→ω±iγ的正负号±分别对应于频率ω的衰减和增加eiωt→e∓γteiωt, 以上三个弛豫的正负号决定于朗道机制.

(21) 式既考虑了元激发的弛豫, 又考虑了各弛豫间关系的正交关系, 这是因为元激发的本征函数是正交的.

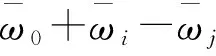
以同样的物理考虑, 我们还可给出计算集体模频移的公式

.

(22)

2.4 q 值的确定

因为TFA的本征值接近于实验值, 我们采用TFA的元激发本征值. 因为TFA的元激发本征函数会导致三模耦合矩阵元的发散, 我们采用bTFA的元激发本征函数.

bTFA中引入参量 q>0 是为了消除三模耦合矩阵元的发散. 如果 q=0，文献 [14] 中的bTFA退化为文献 [13] 的TFA.

文献[42] 对消除发散的方法改进如下.

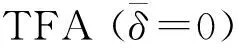
3 计算及结果

3.1 阻尼强度

阻尼强度用 (13) 及 (14) 式来计算.

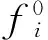
3.2 计算阻尼系数和频移的现在方法

.

(23)

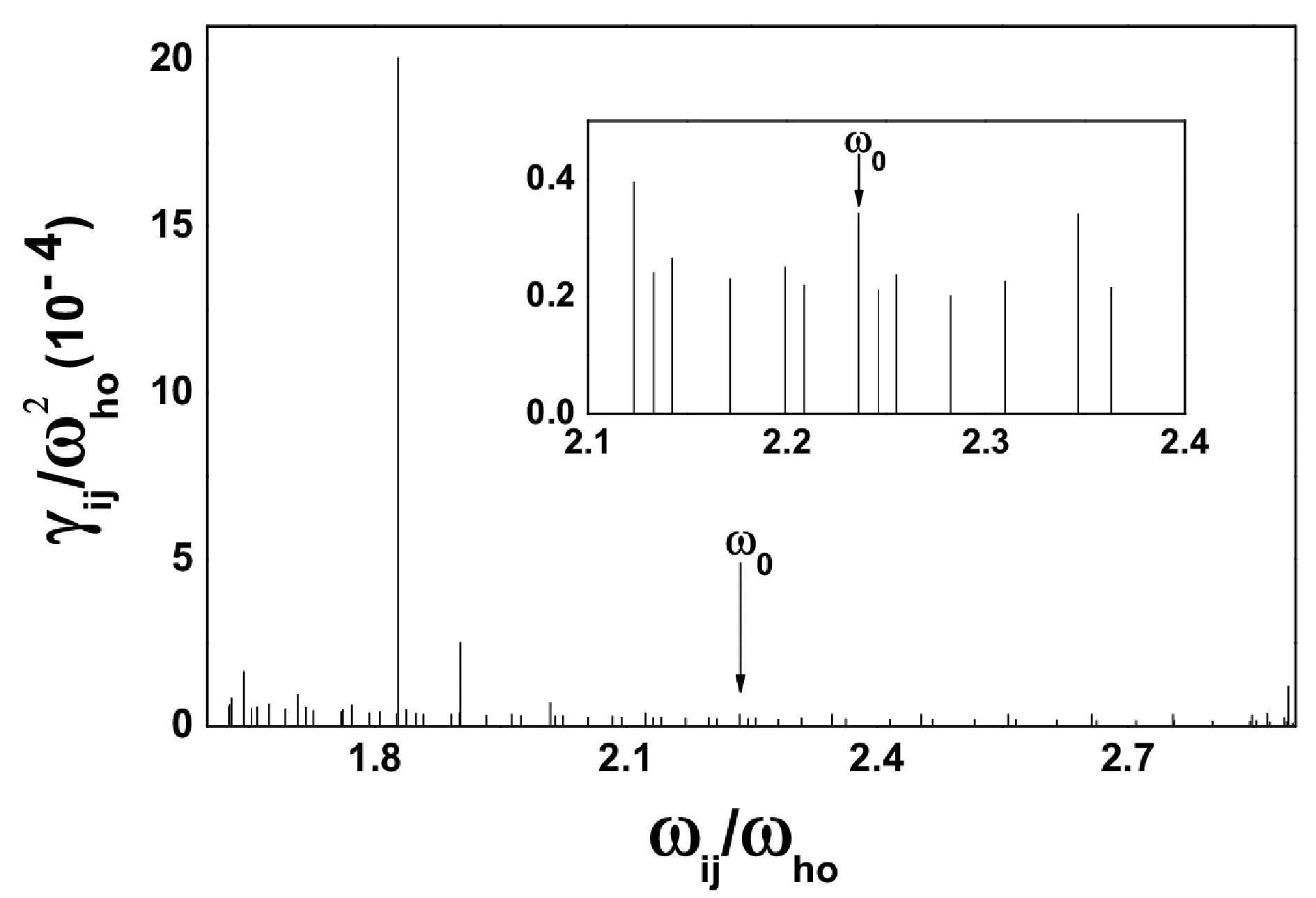
图1 以跃迁ωij为变量的单极子模阻尼强度γij函数线状图Fig. 1 Histogram of damping strength γij as a function of the transition ωij for the monopole mode in the condensate

用迭代的方法计算集体模的阻尼系数.

图2分别给出在温度 KBT/μ=0.4, 0.8, 1.2(相当于T=87.6, 175.2, 262.8nK, 其中 μ=

24.4ħωho) 下 γ0(以ωho为单位) 随 γ (以 ωho为单位) 变化的关系，我们取 N0=150000 和 ωho=1174Hz.图2中用星号表示的三点处γ0=γ, 在KBT/μ=0.4, 0.8, 1.2下的集体模阻尼系数的数值在此三点给出, 分别为0.00079, 0.0012, 0.0015, 相当于0.93, 1.4, 1.8s-1.

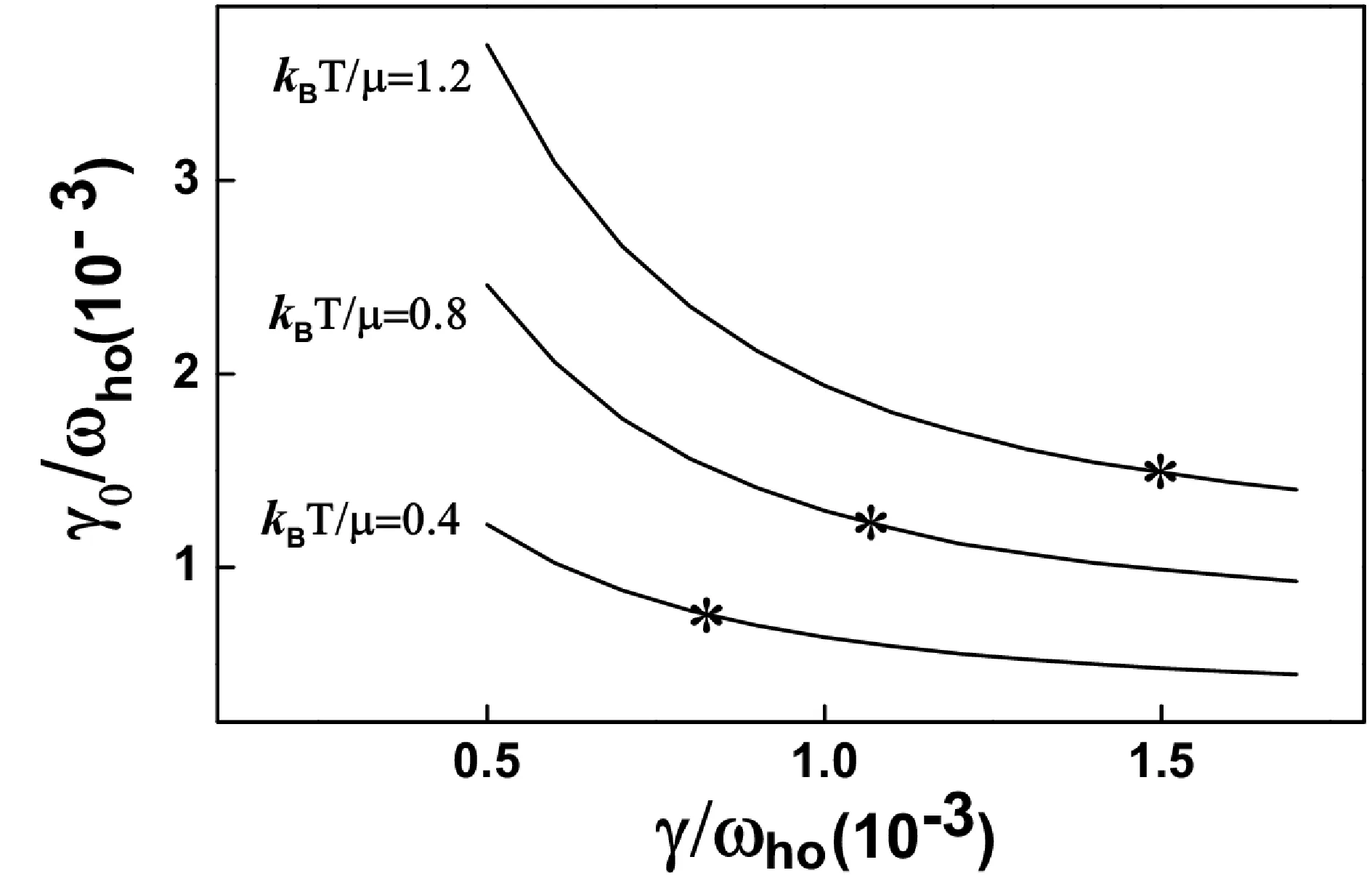
图2 关于朗道阻尼的γ0随γ变化函数图Fig. 2 The γ0 as a function of γ for the Landau damping

把 (22) 式改写成

(24)

由于没有直接的实验报道, 以下我们在取相同原子、粒子数、囚禁频率和温度以及相近集体模频率的条件下, 用球对称凝聚体 (各向异性参量λ=1) 的计算结果与蝶形凝聚体(λ=2.83)[18]和雪茄形凝聚体(λ=0.0646)[20]铷原子的实验结果分别进行间接地对比.

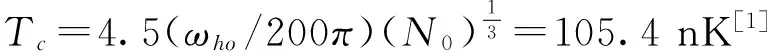
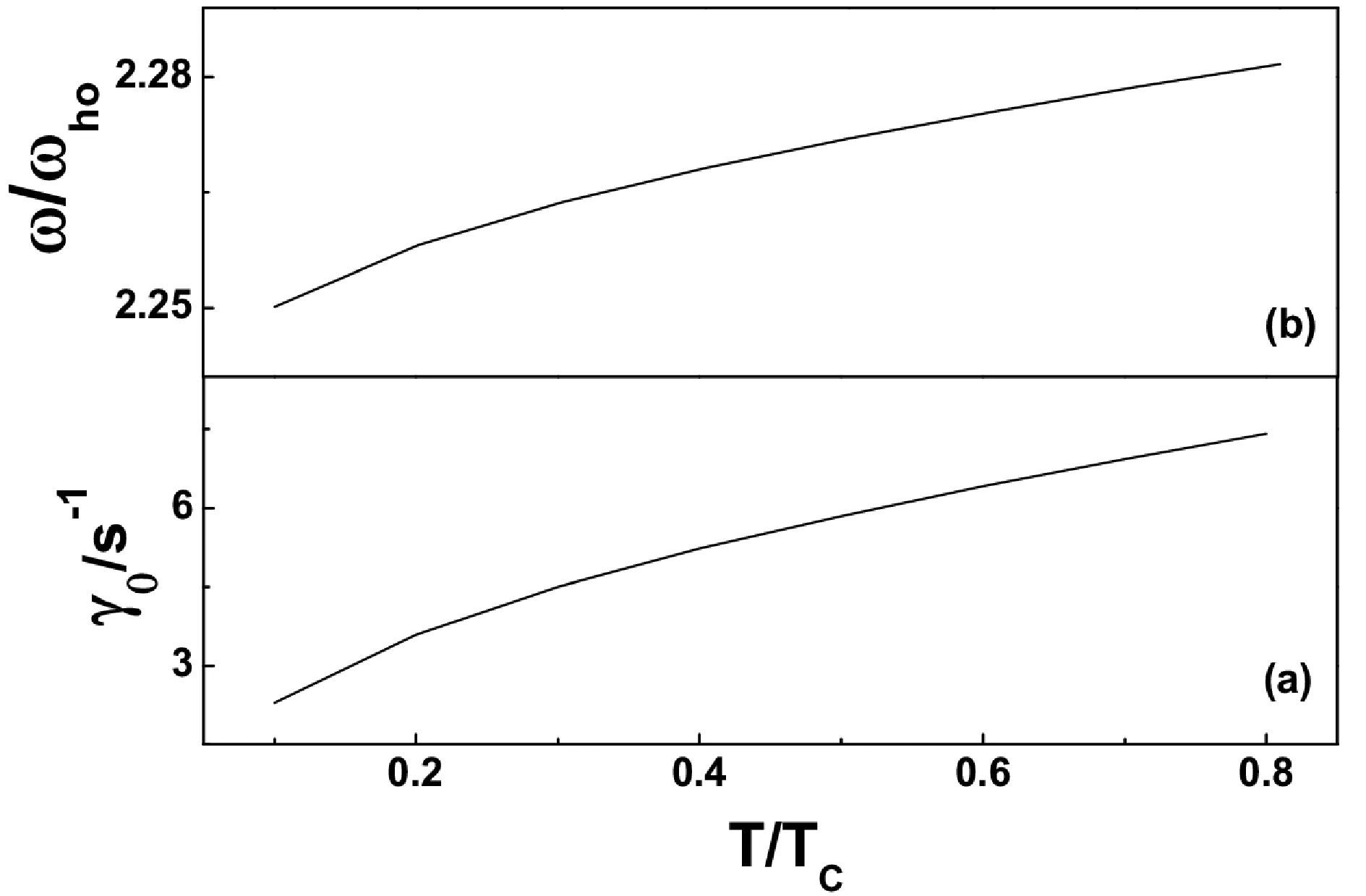
图3 凝聚体集体模的朗道阻尼系数 γ0(a) 和频移 (b) 随温度T的变化图Fig. 3 The landau damping rate γ0(a) and frequency-shift(b) of the collective mode in the condensate as a function of the temperature T

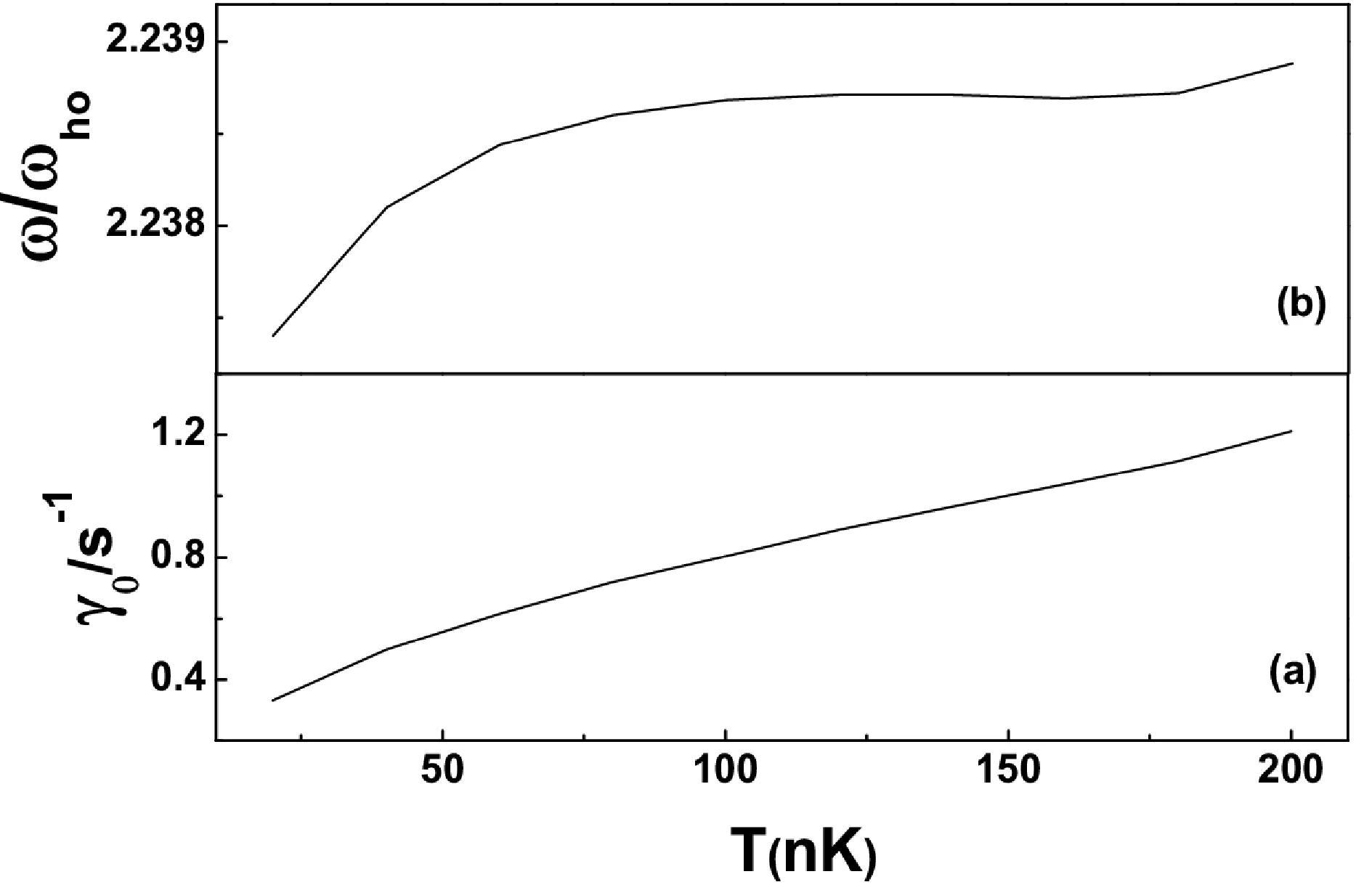
图4 同图3, 但参量另取为N0=200000和ωho=1146 HzFig. 4 Same as Fig. 3 but for N0=200000 and ωho=1146 Hz

图4给出了阻尼 γ0(以 s-1为单位)和频移(以 ω的变化表示，以 ωho为单位)随温度 T(以nK为单位)的函数关系, 我们取文献[20]中的参量 N0=200000 和 ωho=1146Hz. 阻尼计算值大约是文献[20]实验值的1/8, 频移计算值大约是文献[20]实验值的1/4.

比较图3和图4可以看出阻尼和频移的计算值都随着粒子数 N0的增大而增大, 这与实验结果是相符的.

虽然阻尼和频移的计算值比实验值小, 但这是合理的. 我们把(23)式写为

(25)

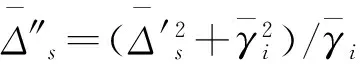
3.3 计算阻尼系数的原来方法

本节考虑满足条件 0.82ω0<ωij<1.18ω0的跃迁并用 (16) 式来计算阻尼系数, 这种方法是原来文献[38-41]计算阻尼系数的方法.

以下，我们在取完全相同参量的条件下, 用原来方法计算阻尼系数, 并与3.2节现在方法的计算结果进行对比.

图5给出了在温度KBT/μ=0.4, 0.8, 1.2时γ0(以ωho为单位)和Δ/2(以ωho为单位)的函数关系, 我们取与图2相同的参数 N0=150000 和 ωho=1174 Hz. 从图5中可以看出当Δ/2的数值在0.015到0.05之间时γ0是缓变的, 因此在KBT/μ=0.4, 0.8, 1.2下γ0的计算数值在此缓变区域内读出, 分别为0.013, 0.029, 0.044, 相当于15, 34, 52 s-1.

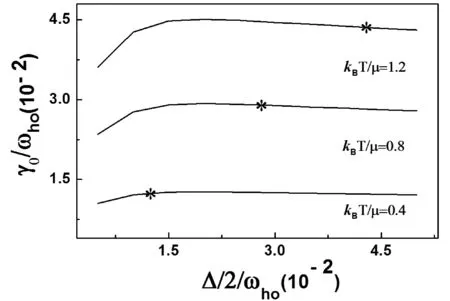
图5 与图2相同, 但是用原来的方法, Δ/2相当于γFig. 5 Same as Fig. 2 but for the previous method, Δ/2 correspond to γ

可以看出阻尼系数图5中用原来方法计算结果大约是图2中用现在方法计算结果的30倍. 这是因为原来的方法只考虑一个弛豫而现在的方法考虑三个弛豫及其各弛豫之间的正交关系. 比较 (16) 式和 (18) 式可以看出 (16) 式中的 Δ/2相当于 (18) 式中的 γ0, 我们可以用 (16) 式以迭代的方法计算 γ0并且能得到相同的结果, 因为在图5中缓变区域内有三个γ0和 Δ/2 相等的用星号标出的点, 这样原来的方法中引入洛伦兹分布函数就相当于考虑一个元激发的弛豫.

以下, 我们在取完全相同参量的条件下, 用原来的方法计算阻尼系数, 和文献[38]数值模拟计算结果进行对比.

图6给出了阻尼系数 γ0(以 ω0为单位) 随温度 KBT/μ 的函数关系, 我们取文献[38]中的参数 ωho=1174 Hz、N0=50000 和150000. 图6 给出的结果与实验结果间接地对比也可以看出原来方法计算的阻尼数值偏大, 图6采用的粒子数接近于文献[20]的粒子数而远大于文献[18]的粒子数, 但计算的阻尼数值却接近于文献[18]的实验值而远大于文献[20]的实验值, 这不符合实验结果的阻尼粒子数依赖. 而图6中给出的解析计算结果和文献[38]的数值模拟计算结果非常接近, 由于计算结果会随着 q 的减小而增大、随着 q 的增大而减小, 所以可以看出我们在解析方法中取 q=1 是合理的.

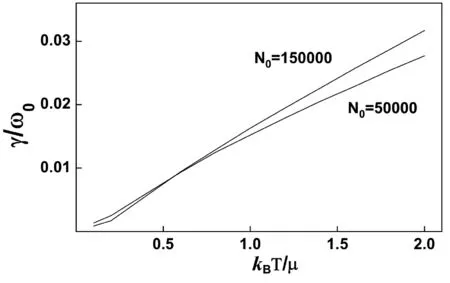
图6 阻尼系数γ随着温度的函数关系 (原来的方法)Fig. 6 Damping rate γ as a function of the temperature (previous method)

4 结 论

我们应用哈特里-福克-博戈留波夫近似研究了球对称铷原子玻色-爱因斯坦凝聚中的单极子模, 解析计算了这个集体模的朗道阻尼和频移. 我们用现在方法计算的结果和实验结果进行间接对比, 讨论了在计算公式中考虑元激发的实际弛豫及其各弛豫间的正交关系合理性. 我们用原来方法计算阻尼系数的结果和数值模拟结果进行直接对比, 说明了基态波函数取高斯分布函数的一级近似的合理性. 因为原来的方法中存在一些缺陷, 阻尼尤其是频移还没有得到充分的研究, 所以我们的改进方法有助于理解玻色-爱因斯坦凝聚集体模阻尼和频移的机制.

[1] Pethick C J and Smith H.Bose-Einsteincondensationindilutegases[M]. Cambridge: Cambridge University Press, 2002: 22.

[2] Stringari S. Collective excitations of a trapped bose-condensed gas [J].Phys.Rev.Lett., 1996, 77: 2360.

[3] Fetter A L. Ground state and excited states of a confined condensed bose gas [J].Phys.Rev. A, 1996, 53: 4245.

[4] Ruprecht P A, Edwards M, Burnett K,etal. Probing the linear and nonlinear excitations of bose-condensed neutral atoms in a trap [J].Phys.Rev. A, 1996, 54(5): 4178.

[5] Dalfovo F, Minniti C, Pitaevskii L P. Frequency shift and mode coupling in the nonlinear dynamics of a bose condensed gas [J].Phys.Rev. A, 1997, 56: 4855.

[6] Morgan S A, Choi S, Burnett K,etal. Nonlinear mixing of quasiparticles in an inhomogeneous bose condensate [J].Phys.Rev. A, 1998, 57(5): 3818.

[7] Hechenblaikner G, Maragò O M, Hodby E,etal. Observation of harmonic generation and nonlinear coupling in the collective dynamics of a Bose-Einstein condensate [J].Phys.Rev.Lett., 2000, 85(4): 692.

[8] Hodby E, Maragò O M, Hechenblaikner G,etal. Experimental observation of beliaev coupling in a Bose-Einstein condensate [J].Phys.Rev.Lett., 2001, 86: 2196.

[9] Maragò O M, Hopkins S A, Arlt J,etal. Observation of the scissors mode and evidence for superfluidity of a trapped Bose-Einstein condensed gas [J].Phys.Rev.Lett., 2000, 84: 2056.

[10] Khawaja U Al, Stoof H T C. Nonlinear coupling between scissors modes of a Bose-Einstein condensate [J].Phys.Rev. A, 2001, 65: 013605.

[11] Hechenblaikner G, Morgan S A, Hodby E,etal. Calculation of mode coupling for quadrupole excitations in a BEC [J].Phys.Rev. A, 2002, 65: 033612.

[12] Liu W M, Fan W B, Zheng W M,etal. Quantum tunneling of Bose-Einstein condensates in optical lattices under gravity [J].Phys.Rev.Lett., 2002, 88(17): 170408.

[13] Ma Y L, Chui S T. Analytical expressions for the hydrodynamic excitation spectrum of Bose-Einstein condensates in axially anisotropic traps [J].Phys.Rev. A, 2002, 65: 053610.

[14] Hu B, Huang G, Ma Y L. Analytical solutions of the Bogoliubov-de Gennes equations for excitations of a trapped Bose-Einstein-condensed gas [J].Phys.Rev. A, 2004, 69: 063608.

[15] Huang G, Szeftel J, Zhu S. Dynamics of dark solitons in quasi-one-dimensional Bose-Einstein condensates [J].Phys.Rev. A, 2002, 65: 053605.

[16] Li C, Ma X, Ma Y L,etal. Resonant interactions of collective modes in a quasi-one-dimensional attractive Bose-Einstein condensate [J].J.Phy.Soc.Jpn., 2013, 82: 044002.

[17] Anderson M H, Ensher J R, Matthews M R,etal. Observation of Bose-Einstein condensate a dilute atomic vapor [J].Science, 1995, 269: 198.

[18] Jin D S, Ensher J R, Matthews M R,etal. Temperature-dependent damping and frequency shifts in collective excitations of a dilute Bose-Einstein condensate [J].Phys.Rev.Lett., 1997, 78(5): 764.

[19] Jin D S, Ensher J R, Matthews M R,etal. Collective excitations of a Bose-Einstein condensate in a dilute gas [J].Phys.Rev.Lett., 1996, 77(3): 420.

[20] Chevy F, Bretin V, Rosenbusch P,etal. The transverse breathing mode of an elongated Bose-Einstein condensate [J].Phys.Rev.Lett., 2002, 88: 250402.

[21] Stamper-Kurn D M, Miesner H J, Inouye S,etal. Collisionless and hydrodynamic excitations of a Bose-Einstein condensate [J].Phys.Rev.Lett., 1998, 81(3): 500.

[22] Onofrio R, Durfee D S, Raman C,etal. Surface excitations in a Bose-Einstein Condensate [J].Phys.Rev.Lett., 2000, 84: 810.

[23] Maragò O, Hechenblaikner J, Hodby E,etal. Temperature dependence of damping and frequency shifts of the scissors mode of a trapped Bose-Einstein condensate [J].Phys.Rev.Lett., 2001, 86(6): 3938.

[24] Mewes M O, Andrews M R, Druten N J V,etal. Collective excitations of a Bose-Einstein condensate in a magnetic trap [J].Phys.Rev.Lett., 1996, 77: 988.

[25] Zaremba E, Griffin A, Nikuni T. Two-fluid hydrodynamics for a trapped weakly-interacting bose gas [J].Phys.Rev. A, 1998, 57: 4695.

[26] Zaremba E, Nikuni T, Griffin A. Dynamics of trapped bose gases at finite temperatures [J].J.LowTemp.Phys., 1999, 116: 277.

[27] Jackson B, Zaremba E. Quadrupole collective modes in trapped finite-temperature Bose-Einstein condensates [J].Phys.Rev.Lett., 2002, 88: 180402.

[28] Jackson B, Zaremba E. Accidental suppression of Landau damping of the transverse breathing mode in elongated Bose-Einstein condensates [J].Phys.Rev.Lett., 2002, 89: 150402.

[29] Morgan S A, Rusch M, Hutchinson D A W,etal. Quantitative test of thermal field theory for Bose-Einstein condensates [J].Phys.Rev.Lett., 2003, 91: 250403.

[30] Morgan S A. The response of Bose-Einstein condensates to external perturbations at finite temperature [J].Phys.Rev. A, 2004, 69: 023609.

[31] Giorgini S. Damping in dilute Bose gases: a mean-field approach [J].Phys.Rev. A, 1998, 57: 2949.

[32] Giorgini S. Collisionless dynamics of dilute bose gases: Role of quantum and thermal fluctuations [J].Phys.Rev. A, 2000, 61: 063615.

[33] Pitaevskii L P, Stringari S. Landau damping in dilute bose gases [J].Phys.Lett. A, 1997, 235: 398.

[34] Fedichev P O, Shlyapnikov G V, Walraven J T M. Damping of low-energy excitations of a trapped Bose-Einstein condensate at finite temperatures [J].Phys.Rev.Lett., 1998, 80(11): 2269.

[35] Reidl J, Csordás A, Graham R,etal. Landau damping of bogoliubov excitations in optical lattices at finite temperature [J].Phys.Rev. A, 2000, 61: 043606.

[36] Tsuchiya S, Griffin A. Landau damping of bogoliubov excitations in optical lattices at finite temperature [J].Phys.Rev. A, 2005, 72: 053621.

[37] Guilleumas M, Pitaevskii L P. Landau damping of transverse quadrupole oscillations of an elongated Bose-Einstein condensate [J].Phys.Rev. A, 2003, 67: 053607.

[38] Guilleumas M, Pitaevskii L P. Temperature-induced resonances and Landau damping of collective modes in Bose-Einstein condensed gases in spherical traps [J].Phys.Rev. A, 1999, 61: 013602.

[39] Ma X, Ma Y L, Huang G. Analytical calculations on Landau damping of collective modes in anisotropic Bose-Einstein condensates [J].Phys.Rev. A, 2007, 75: 013628.

[40] Ma X, Zhou Y, Ma Y L,etal. Landau damping of collective modes in a harmonically trapped Bose-Einstein condensate [J].Chin.Phys., 2006, 15 (8): 1871.

[41] Ma X, Ma Y L, Huang G. Landau damping of collective modes in a harmonicall trapped Bose-Einstein condensate [J].Chin.Phys.Lett., 2007, 24 (3): 616.

[42] Chai Z, Zhou Y, Ma X. Landau damping and frequency-shift of monopole mode in an elongated rubidium Bose-Einstein condensate [J].ActaPhys., 2013, 62(13): 130307(in Chinese)[ 柴兆亮, 周昱, 马晓栋. 雪茄形铷原子玻色-爱因斯坦凝聚中单极子模的朗道阻尼和频移[J]. 物理学报, 2013, 62(13): 130307]

[43] Ma X, Yang Z, Lu J,etal. Landau damping of collective mode in a quasi-two-dimensional repulsive Bose Einstein condensate [J].Chin.Phys. B, 2011, 20(7): 070307.

[44] Yang Z, Chai Z, Li C,etal. Landau damping of collective mode in a quasi-one-dimensional repulsive Bose-Einstein condensate [J].Commun.Theor.Phys., 2012, 57(5): 789.

Landau damping and frequency-shift of a monopole mode in a spherical rubidium Bose-Einstein condensate

PENG Sheng-Qiang, RAHMUT Arzigul, MA Xiao-Dong

(College of Physics and Electronic Engineering, Xinjiang Normal University, Urumchi 830054, China)

The Landau damping and frequency-shift of a monopole mode in a spherical rubidium Bose-Einstein condensate are investigated by using the Hartree-Fock-Bogoliubov approximation. The damping rate and frequency-shift magnitude and their temperature dependence are analytically calculated by using the parameters of particle number and traping frequency in the study of numerical simulation and experiment in existence. In the calculation, the practical relaxations of the elementary excitations and the orthometric relation among them are taken into account to obtain the calculation formula for damping and frequency-shift, and the first approximation of Gaussian distribution function is employed for the ground-state wavefunction to eliminate the divergence of the three-mode coupling matrix elements. Our calculation results are directly and indirectly compared with the numerical simulation ones and experimental ones, respectively. And all the comparison illustrate that our method is reasonable.

Bose-Einstein condensate; Landau damping and frequency-shift; Hartree-Fock-Bogoliubov approximation; Thomas-Fermi approximation

103969/j.issn.1000-0364.2015.12.018

2014-03-18

国家自然科学基金项目(11264039);新疆理论物理重点学科(LLWLY201202, LLWLY201203);新疆师范大学研究生科技创新项目(20131234)

彭胜强(1987—),男，四川绵阳人，硕士研究生，主要研究领域为理论物理.

马晓栋. E-mail: xdma07@aliyun.com

O561

A

1000-0364(2015)06-1018-09