缩尺结构模型的相似荷载优化设计
宋泰宇 沈 殷 李国平
(同济大学桥梁工程系,上海200092)
1 引言
结构模型试验是确定或探索结构受力性能的重要手段之一。根据不同的试验目的、要求和内容,结构模型通常可分为两类:小结构模型和相似模型[1]。受试验场地的限制,为了节约材料、降低荷载吨位,相似模型试验大多采用缩尺模型进行。设计缩尺模型试验时,首先需要根据相似原理将原型结构等效成理想缩尺模型。对于静载试验,相似原则包括几何相似、边界条件相似和物理过程相似三个方面[1-2]。而在物理过程的相似模拟中,相似荷载的确定往往是缩尺模型试验设计中的难点。根据相似原理,若理想缩尺模型采用和原型结构相同的材料设计,则需要在缩尺模型上加载n-1(1:n为缩尺比)倍的自重进行恒载补偿。缩尺比越小,需要补偿的恒载就越大,而大吨位的均布荷载加载在试验室条件下通常很难实现。
目前,对于简单结构的简单荷载工况,如简支梁的恒载补偿等,相似荷载的设计方法主要有:①采用等分点加载方式,相似荷载的设计满足结构某一关键截面的某一内力等效[3];② 采用等分点加载方式,相似荷载的设计基于合力相等原则,数据后处理时对试验结果考虑一定的系数修正效应[4],但文献[4]并未详细说明修正系数的等效原理。
对于连续梁等复杂结构,或在活载补偿等复杂工况下,相似荷载的设计方法主要有:①采用等分点加载,满足某些关键截面的内力等效[5-6];②利用多点配重(方式包括堆摊和悬吊)或杠杆系统的方式进行拟均布荷载等效[5-15],这种方法最常用,相似度也最好,但当缩尺比较小时,需要大量配重材料和多点加载设备,经济性较差[16];③当结构中某部分不是研究对象,并且其上作用的理想缩尺荷载不影响其他部分时,如斜拉桥桥塔的恒载补偿等,可不施加相似荷载,而只将实测值与理想缩尺模型补偿值进行叠加[9,14,16]。当前的缩尺模型试验设计中,还缺乏明确的相似荷载优化设计方法,或采用经验法,或针对某具体试验模型而设计,适用范围有一定的局限性。
本文针对缩尺结构模型的相似荷载优化设计方法进行了研究,在模型试验中常用的有限多点集中力加载方式的基础上,给出设计参数和自变量的集合,以约束条件推得因变量,以表征量的相似误差函数为优化目标函数,提出了相似荷载优化设计的基本思路和流程,以此推导了简支梁和连续梁的最优相似荷载设计的解析解,验证了解析解和数值解的一致性,并在基本思路的基础上,对优化设计中可能出现的多维度难点问题进行讨论,且均提出了初步的解决方法,最后进一步根据空间杆系有限元方法,对空间曲线梁桥的恒载的相似荷载进行了优化设计。
2 优化设计思路
模型试验中,相似荷载的模拟和施加常用多点集中力加载方式实现。加载点的数量通常由试验加载的空间条件和设备条件来决定;而加载点的作用位置和荷载大小则是相似荷载的主要设计参数。根据模型试验的试验目的,部分截面的荷载效应是分析试验模型的受力性能和特征的主要约束条件,对于这些主控荷载效应要求能够完全等效,如简支梁弯曲性能试验中,跨中截面的弯矩或应力应完全等效[6]。当相似荷载设计参数数量大于约束条件个数时,设计参数可以有无穷多解。为此,相似荷载设计中可以进一步提取模型试验中重要的表征量进行优化,如简支梁弯曲性能试验中,取主梁的弯矩为优化表征量。优化的目标函数采用优化表征量的均方根误差,使所寻求的最优解满足相似误差最小的原则。当设计参数数量足够多的时候,模型试验的荷载效应可以在很多方面和理想缩尺模型相似,从而使模型试验能够尽可能的反映实际结构的受力性能,提高试验的模拟效果。
缩尺结构模型的相似荷载优化设计属于有约束的优化问题。优化的目标即使优化表征量的相似误差函数取到极小值,寻求的优化解是相似荷载的设计参数,而优化解受到制定的约束条件的限制。可以表达为:

约束条件:gi(x)=0;i=1,2,…,m,m < n,这里x=[x1x2… xn]T,表示相似荷载的设计参数;gi(x)=0表示设计参数的约束条件;W=f(x)表示优化目标函数;f,gi是设计参数的函数。优化设计的最优解即满足约束等式gi(x)=0,且函数f(x)在其上取得极小值的特定集合根据上述基本思想和数学表达,缩尺模型的相似荷载优化设计的具体流程如下:
第一步:根据试验的实际加载条件,确定相似荷载设计参数的集合X=[x1x2… xn]T;
第二步:根据模型试验的试验目的和模型结构的受力性能,设计约束条件gi(x)=0;i=1,2,…,m,m <n;
第三步:根据前两步确定的设计参数和约束方程,合理确定自变量和因变量,因变量的个数等于m,记其集合为⊂X;自变量集合记为xk+n-m-1]⊂X,其个数等于 n -m;
第四步:根据试验的研究目标,确定优化设计的表征量P,得到表征量的均方根误差,即相似荷载的优化目标函数W=f(X);
第五步:利用解析法或数值法,对优化问题进行求解,得到最优化加载方案的设计参数完成缩尺模型的相似荷载优化设计。
3 解析法
在缩尺模型的相似荷载优化设计中,优化的目标函数采用优化表征量的均方根误差。当目标函数可以显式表达,且表达式较为简单时,可以直接利用微分法求解最优解。相似荷载优化设计的解析解和目标函数表示如下:

式中,Wa=f(X)为解析解法的目标函数;f是自变量的连续函数;Pideal(x),Psim(x)分别表示理想缩尺荷载和相似荷载的表征量,是变量的的连续函数;l表示考虑进行优化的范围,其他符号同前。
令目标函数对每个自变量偏导为零,可得到n-m个方程,从而可解得n-m个自变量的解集再代回约束条件,可求解因变量集合二者的合集即为最优化相似荷载的设计参数集合
缩尺模型相似荷载的设计一般包括相似恒载补偿和相似活载两个荷载工况设计,对应的理想缩尺模型所受荷载一般包括均布力、均布力偶、集中力等。下面以结构模型试验中最简单、常见的等截面简支梁为例,对其缩尺模型的恒载补偿进行相似荷载优化设计,求解最优化设计参数的解析解。
等截面简支梁的理想缩尺模型上需要补偿的恒载为沿全梁长l的均布力q(图1(a)),试验加载条件假定为常见的分载梁对称加载(图1(b))。相似荷载的设计参数集合采用 X=[F L]T,其中,F为加载点荷载大小,L为加载点中距;考虑相似荷载与理想补偿恒载作用下的模型跨中正弯矩相等,可得约束条件:
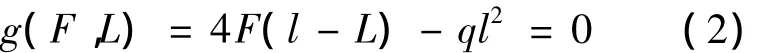
自变量集合取 Xdep=[L],因变量集合为Xindep=[F];优化设计的表征量P为主梁弯矩M(x),优化设计的考虑范围为全梁长l。理想补偿恒载作用下和相似荷载作用下的结构模型的表征量,即主梁弯矩,可表示为(由对称性这里取半结构):


图1 相似荷载和理想恒载补偿图示Fig.1 Similar load and ideal reduced scale load
图2 中绘出了相似荷载和理想补偿恒载作用下的弯矩分布曲线,可以看出两者在满足式(2)的前提下,沿梁长的弯矩分布具有一定的误差。优化的相似荷载是使两者的均方根误差达到最小值,进而满足最优化解的要求。据此,求得表征量的均方根误差,通过代入式(2),消去因变量F,可得到目标函数f为自变量L的函数f(L):
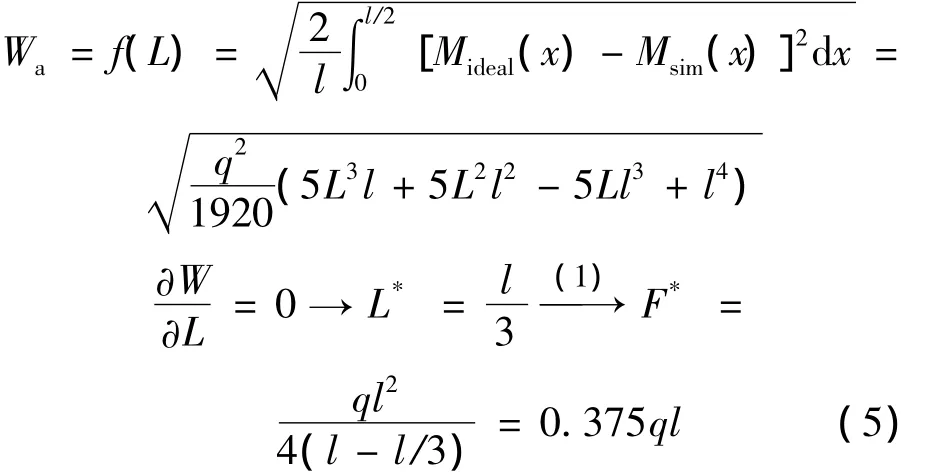
表1中列出了常用梁式桥缩尺模型相似荷载的优化设计结果,其中最不利相似活载根据规范按影响线加载方式获得。

图2 相似荷载和理想补偿恒载作用下的弯矩分布Fig.2 Bending moment under similar load and ideal reduced scale load

表1 常用梁式桥缩尺模型相似荷载的优化设计结果Table 1 Optimization design results of similar load on raduced scale beam model
4 数值法
优化问题的求解中,显式、可导的目标函数可以得到解析解,但是对于多维复杂的目标函数,可能无法求得解析解,可采用搜索的方式求得数值解。当出现以下情况:①试验结构的理想缩尺模型所受荷载较复杂,如变截面桥梁的缩尺模型恒载补偿;②自变量较多,多维目标函数较复杂,偏导运算可能无法直接求解;③对于复杂结构,如预应力结构等,表征量表达式不易推导解析式,无法得到目标函数解析式;④试验加载条件不同,等效加载模型的加载图示无法统一时,相似荷载的优化设计参数的解析解求解费时或无法实现;另外,对某一特定模型结构,推导解析解也缺乏通用性,可基于有限元软件分析结果,搜索得到某一特定缩尺模型相似荷载的设计参数数值解。优化相似荷载的数值解法采用搜索法进行求解,可以表达为

式中,Wn=f(X)为数值解法的目标函数;f是自变量的离散函数;Pideal,k,Psim,k分别表示理想缩尺荷载和相似荷载的表征量,是变量的的离散函数,n表示优化设计考虑单元的数目,其他符号同前。在可行域内选取一系列满足约束条件的设计参数集X1,X2,…分别求解出对应的优化表征量,得到一系列目标函数数值f(X1),f(X2),…取到极小值时的自变量集合,自变量集合代入约束条件,可求解因变量集合X*dep,二者的合集即为最优化相似荷载的设计参数集合 X=根据微积分原理Wa,就是说,只要有限元模型单元划分得足够细,得到的数值解是足够接近精确的解析解的。
为了方便讨论,仍以等截面简支梁为例,进行相同条件下的恒载补偿优化设计。相似荷载的设计参数、约束条件、自变量集合、因变量集合、表征量、优化设计的考虑范围均不变,与解析解法中相同。利用Midas软件建立等截面简支梁的缩尺模型,模型梁长l=3 m,沿梁长等距划分100个单元,假设理想缩尺恒载补偿为q=45 kN/m,自变量L在0 m到1.68 m等距选取15个离散值和三分距1.0 m。根据式(2)确定因变量F,输出理想缩尺荷载和16个相似荷载作用下的单元弯矩值(图3)。根据式(7)得到各自变量对应的目标函数数值曲线(图4)。

由目标函数数值曲线可以发现,目标函数随自变量的增加先递减后递增,且当自变量L=1.0 m时,目标函数值达到极小值,故最优化相似荷载的设计参数数值解为 X*=[F*L*]T=[50.63 kN 1.0 m]T。
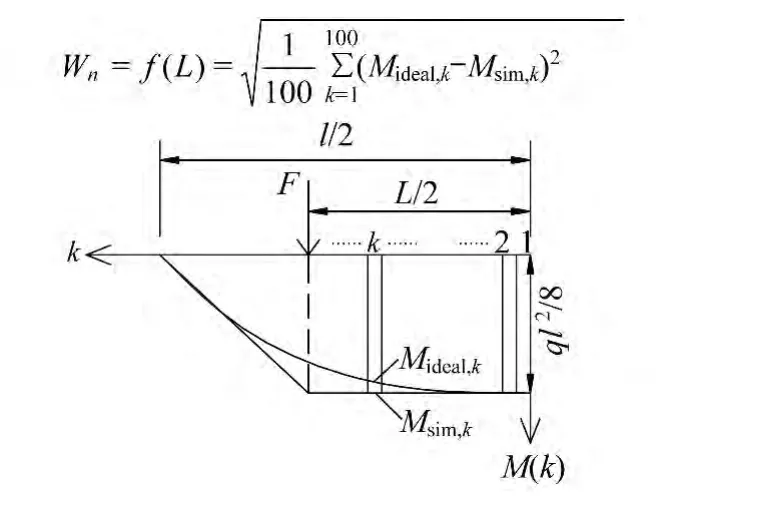
图3 相似荷载和理想补偿恒载作用下的弯矩分布Fig.3 Bending moment under similar load and ideal reduced scale load

图4 各设计方案目标函数值变化曲线Fig.4 Objective function values in different designs
将该结果与 X*=[F*L*]T=[0.375ql l/3]T进行对比,代入已知条件 q=45 kN/m,l=3 m,得到相应解析解为[50.625 kN 1 m]T,与数值法的结果一致(图4),说明数值解法是正确的,其结果的精度也是很高的。
5 多维度难点问题
上面讨论的是在两点对称加载基础上的等截面简支梁恒载补偿的优化设计,是优化设计中最简单的情况。实际缩尺结构模型的相似荷载优化设计可能会较为复杂,下面对优化设计中可能出现的多维度难点问题进行讨论,并提出初步的解决方法。
(1)多自变量求解。采用数值法求解时,当自变量个数为一个时,目标函数值由自变量唯一确定;当自变量个数为两个时,目标函数值由一个二维数组确定;当自变量个数为n时,目标函数值由n维自变量矩阵确定。要找到目标函数值的极小值,需要对每一自变量在其可行域内取离散值,搜索次数呈方次增加,工作量巨大。为减少计算量,可以采用变量分离、反复迭代的思路,将多变量极值问题化为单变量极值问题进行求解。下面以三个自变量为例,求解目标函数值W=f(A,B,C)取到极小值Wmin时最优化相似荷载的设计参数集合[A*B*C*]的流程图如图5所示。

图5 多自变量目标函数求解流程图Fig.5 Flow chart of solution of objective function with multiple variables
(2)多目标函数加权。当优化设计的表征量为多个时,对应的目标函数也为多个,而不同目标函数取到极小值时的自变量可能不同,需要将多个目标函数综合为单目标函数以进行比较,故可将多个目标函数加权平均为一个“综合目标函数”,该综合目标函数取到极小值时的自变量为最优化相似荷载设计的自变量,相应的设计参数为最优化设计参数。目标函数的加权平均公式:
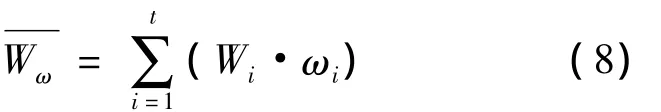
式中,t表示表征量,即目标函数W的个数;ωi为Wi的权重,其他符号同前。
对于不同目标函数,其物理意义不同,单位不同,对综合目标函数的影响强度也不同,所以权重确定可分为两个方面:①统一目标函数的比较尺度;②量化目标函数的重要程度。对应方法是:
(1)将不同目标函数值均除以所有方案中该目标函数的最小值:

(2)当目标量较少(不超过3个)时,试验者可根据经验和试验目的直接判断,给出权重系数当优化表征参数超过3个时,可利用层次分析法,由成对比较阵求权向量的特征根法确定权重系数ω(2)i。最后,给出Wi的组合权重系数为
(3)如果优化设计时只考虑结构模型中一部分截面上的表征量时,则式(1)的积分区间用该部分截面的区间,式(5)的累加单元用该部分截面的单元。
(4)根据试验研究目的和构件的重要性和自身特点,可在目标函数中加入不同截面的权重系数,人为给出各截面在优化时的加权量B(x)或B(k),则式(1)、式(6)用下面两式替代。当表征量为弯矩,权重系数为柔度系数时,目标函数的意义类似于弯曲能量的误差函数。

(5)当优化设计的约束条件为不等式时,可将设计参数均当做自变量考虑,应用解析法或数值法求解,并检验其最优解是否满足不等式约束,若满足,则即为最优设计参数;若不满足,则将不等式取边界值化为等式,求解等式约束问题。
6 三跨曲线梁的相似荷载优化设计
基于国家自然科学基金项目《体外预应力混凝土曲线桥复杂空间力学行为及失效机理》的缩尺模型静载试验,应用上述设计方法,对一三跨体外预应力曲线梁的恒载(自重+二期)进行相似荷载的优化设计。模型梁采用1:8缩尺比,中心线弧长(3+3.75+3)m=9.75 m,曲率半径 5 m,配置四根体外预应力钢束,一次落架施工。利用Midas软件建立缩尺模型,主梁采用梁单元,体外束采用桁架单元。
试验加载条件为每跨一分载梁对称加载,即有6个加载点。相似荷载的设计参数:①中跨加载点荷载;②边跨加载点荷载;③中跨加载点中距;④边跨加载点中距;⑤边跨加载点连线中点位置;考虑相似荷载与理想补偿恒载作用下的模型中跨跨中正弯矩相等和中支点负弯矩相等为约束条件;自变量取为上述设计参数③-⑤,因变量为设计参数①、②;优化设计的表征量为体外预应力筋应力和不考虑预应力效应的主梁挠度;优化设计的考虑范围均为全梁长。
本缩尺模型相似荷载的设计属于多自变量、多目标函数的优化问题,采用数值法,共建立17个有限元模型对三个自变量进行优化设计,得到最优化相似荷载设计参数的数值解为:①中跨加载点荷载28.8 kN;②边跨加载点荷载22.2 kN;③中跨加载点中距125 cm;④边跨加载点中距100 cm;⑤边跨加载点连线中点位置居边跨跨中。恒载补偿加载立面如图6所示。

图6 试验梁恒载补偿加载立面示意图(单位:kN)Fig.6 Elevation of dead load compensation(Unit:kN)

图7 最优相似荷载和理想缩尺荷载作用下的表征量Fig.7 Characteristic parameters people’s under optimized similar load and ideal reduced scale load
最优设计的相似荷载和理想缩尺荷载作用下的两个表征量沿全梁长的分布如图7所示。从图7(a)和图7(b)均可以看出,两个表征量沿全梁长的分布非常接近,相似度很好,所以该缩尺结构模型的试验结果可以较真实地反映实际结构的受力性能。
7 结论
(1)本文针对缩尺结构模型的相似荷载优化设计,根据相似误差的概念并结合优化理论,以表征量的相似误差函数作为优化的目标函数,提出了相似荷载优化设计的基本思路、流程和求解方法。
(2)推导了简支梁和连续梁的最优相似荷载设计的解析解,并验证了简支梁恒载补偿最优解析解和数值解的一致性,基于经验的简支梁三分点恒载补偿加载符合解析解。
(3)在基本优化设计思路的基础上,针对多自变量、多目标函数等多维度难点问题,提出对应的初步解决方法,从而可将优化设计扩展到更为复杂的情况中,并对三跨曲线梁桥恒载的相似荷载进行了优化设计,该设计属于多自变量、多目标函数的复杂优化问题,优化结果表明最优设计下缩尺模型的相似度很好。
[1] 李德寅,王邦楣,林亚超.结构模型试验[M].北京:科学出版社,1996.Li Deyin,Wang Bangmei,Lin Yachao.Test of structural Moclel[M].Beijing:Science Press,1996.(in Chinese)
[2] 章关永.桥梁结构试验[M].北京:人民交通出版社,2002 Zhang Guanyong.Test of bridge structures[M].Beijing:China Communication Press,2002.(in Chinese)
[3] 鄢芳华,沈殷,李国平,等.体外预应力混凝土梁模型试验初步研究[J].结构工程师,2003(3):66-70.Yan Fanghua,Shen Yin,Li Guoping,et al.Preliminary study on model test of externally prestressed concrete beam[J].Structural Engineers,2003(3):66-70.(in Chinese)
[4] 中华人民共和国住房和城乡建设部.GB 50152—2012混凝土结构试验方法标准[S].北京:中国建设工业出版社,2012.Ministry of Housing and Urban-Rural Development of the People's republic of China.GB 50152—2012 Standard methods for testing of concrete structures[S].Beijing:China Architecture and Building Press,2012.(in Chinese)
[5] 毛玉东.港珠澳大桥组合连续箱梁模型试验研究[D].武汉:武汉理工大学,2012.Mao Yudong.Model test of continuous composite box girder in Hong kong-Zhuhai-Macao Bridge[D].Wuhan:Wuhan University of Technology,2012.(in Chinese)
[6] 刘自明.桥梁结构模型试验研究[J].桥梁建设,1999,(4):1-7.Liu Ziming.Test study of bridge structure models[J].Bridge Construction,1999,(4):1-7.(in Chinese)
[7] 汪存书,郑和晖,陈富强,等.龙河特大桥墩梁结合部模型试验设计[J].结构工程师,2013,29(5):119-125.Wang Cunshu,Zheng Hehui,Chen Fuqing,et al.Model design of the pier-beam joint in the Longhe super large bridge[J].Structural Engineers,2013,29(5):119-125.(in Chinese)
[8] 沈锐利,齐东春,唐茂林.杭州江东大桥静力特性全桥模型试验研究[J].土木工程学报,2011,44(1):74-80.Shen Ruili,Qi Dongchun,Tang Maoling.Model test study of the static property of the Jiangdong bridge in Hangzhou[J].China Civil Engineering Journal,2011,44(1):74-80.(in Chinese)
[9] 余毅,余天庆,乐韩燕.吉林兰旗松花江特大桥施工阶段及成桥静力模型制作[J].世界桥梁,2008(1):73-75.Yu Yi,Yu Tianqing,Le Hanyan.Fabrication of static force model for Jilin Lanqi Songhua River bridge at construction and completion stages[J].World Bridges,2008(1):73-75.(in Chinese)
[10] 王天亮,程宝辉.沈阳市富民桥全桥模型试验研究方法介绍[J].桥梁建设,2006(B05):70-74.Wang Tianliang,Cheng Baohui.Method of overall bridge model test and study of Fumin bridge in Shenyang[J].Bridge Construction,2006(B05):70-74.(in Chinese)
[11] 冯剑.矮寨特大悬索桥缩尺模型设计研究[D].长沙:长沙理工大学,2010.Feng Jian.The research on scale model design of Aizhai suspension bridge[D].Changsha:Changsha U-niversity of Technologyk,2010.(in Chinese)
[12] 高小妮.多塔斜拉—自锚式悬索组合体系桥梁结构理论分析与模型试验研究[D].西安:长安大学,2012.Gao Xiaoni.Theoretical analysis and model test study on cable-stayed and self-anchored suspension combination bridge with multi-tower[D].Xi’an:Chang’an University,2012.(in Chinese)
[13] 胡建华,沈锐利,张贵明,等.佛山平胜大桥全桥模型试验研究[J].土木工程学报,2007,40(5):17-25.Hu Jianhua,Shen Ruili,Zhang Guiming,et al.A total bridge model study of the Pingsheng bridge in Foshan[J].China Civil Engineering Tournal,2007,40(5):17-25.(in Chinese)
[14] 安群慧,刘自明.荆州长江公路桥整体模型试验研究[J].桥梁建设,2002(2):15-18.An Qunhui,Liu Ziming.The whole model test study for Jingzhou Changjiang River highway bridge[J].Bridge Construction,2002(2):15-18.(in Chinese)
[15] 李亚非,颜东煌.大型三塔斜拉桥铝合金试验模型的研制[J].长沙交通学院学报,2000,16(3):37-41.Li Yafei,Yan Donghuang.Development and manufacture of a large aluminum test model of three tower cable-stayed bridge[J].Journal of Changsha Communications University,2000,16(3):37-41.(in Chinese)
[16] 项贻强,吴孙尧,段元锋.基于刚度相似原理的斜拉桥模型设计方法[J].实验力学,2010(4):438-444.Xiang Yiqing,Wu Sunyao,Duan Yuanfeng.Design method of small-scale cable-stayed bridge based on stiffness similarity theory[J].Journal of Experimental Mechanics,2010,(4):438-444.(in Chinese)

