某开口单层网壳结构设计及稳定性分析

程杨苟 张晓光

(1．同济大学建筑工程系，上海200092;2．同济大学建筑设计研究院(集团)有限公司，上海200092)

1 工程概况

某会议中心位于福建省龙岩市，主体结构为钢筋混凝土框架，其外部采用玻璃幕墙屋盖，屋盖结构体系采用椭球面单层网壳。网壳平面投影为半椭圆形，长边约32 m，短边约30 m，投影面积约564 m2，开口处矢高约11 m，建筑效果见图1。

网壳支撑于下部钢筋混凝土结构地下室顶板，与内部钢筋混凝土结构的会议室完全脱离。网壳前端开口，开口边为不规则空间曲线，其跨度约30 m，最高点高度约11 m，网壳开口部分与主体结构的间隙采用玻璃幕墙封闭。网壳采用三向斜交三角形网格，三角形大部分为等边三角形，杆件长度约为2．4 m，局部为不等边三角形，杆件长度在0．8 m～2．5 m之间。为获得较好的建筑美学效果，网壳横向和斜交的杆件全部采用统一外形尺寸的矩形管截面，截面主轴垂直屋面向内，节点采用焊接鼓形刚接节点(图2(a))，屋盖支撑在下部钢筋混凝土地下室顶板上，为避免对钢筋混凝土地下室顶板产生弯矩，支座采用焊接的固定铰支座(图2(b))，结构计算模型见图3。

图1 建筑效果图Fig．1 Architectural illustration

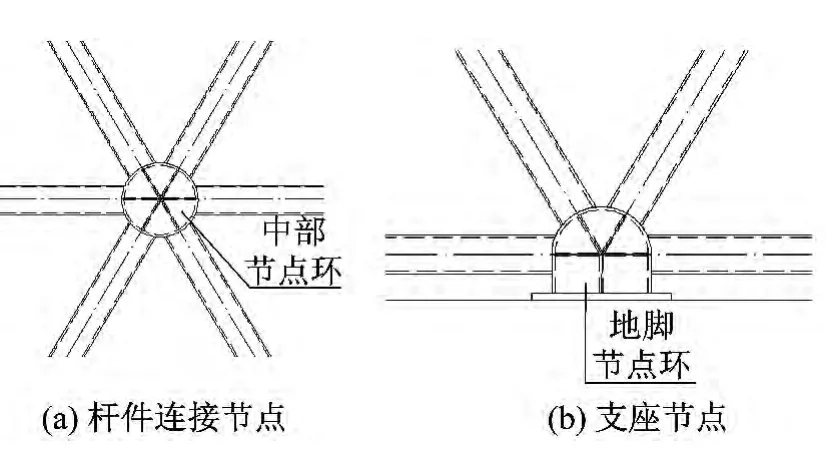
图2 结构典型节点示意图Fig．2 Schematic plots of typical nodes

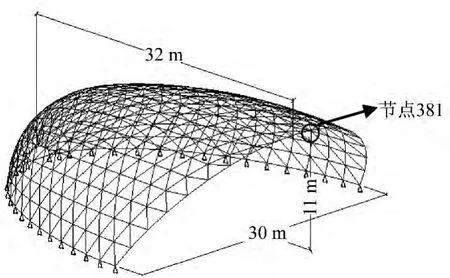
图3 结构计算模型Fig．3 Numerical structure model

2 结构方案设计

2．1 计算参数的选取

工程设防烈度为6度，设计基本地震加速度为 0．05 g，第一组，特征周期 Tg=0．35 s，Ⅱ类场地。基本风压按100年重现期取0．45 kN/m2，地面粗糙度为B类。屋面恒载1．0 kN/m2，活载0．5 kN/m2，考虑温度变化±25℃。

2．2 结构分析与设计

2．2．1 初选方案

使用SAP2000软件进行结构计算，单个杆件为1单元，节点为刚接，固定铰接支座。初步设计时，用同一尺寸的250×100方钢管截面作为网壳杆件截面，钢材材料选用Q345B。

经计算分析，得到网壳的应力比如图4所示。

图4 结构应力比图Fig．4 Plot of stress ratio

网壳上与节点309连接的杆件903的应力比最大，最大应力比为0．886，其余部位的杆件最大应力比均在0．75以下。

结构在1．0恒载+1．0活载工况作用下，网壳开口边的顶点处节点381(图3)的竖向位移最大，最大竖向位移为118 mm，大于《空间网格结构技术规程》以下简称《网格规程》［1］要求的l/400=30 m/400=75 mm(l为网壳最大横向跨径)。网壳的内力图见图5(由于结构布置和荷载分布对称，取半跨分布图)。

图5 D+L作用下结构内力分布图Fig．5 The structure internal force distribution under D+L load

由图5可知，网壳内力较大的杆件大都集中在图中虚线所围区域。各类杆件(图5(c))的受力有如下特点:

(1)斜杆。网壳的斜杆受轴压为主，离开口边越远，各排斜杆所受的压力渐小;单根斜杆轴压力由顶点向根部逐渐加大，呈现较为明显的拱受力状态;与节点309连接的杆件872受的压力最大，为621 kN。与节点309连接的另一根杆件903受的拉力最大，大小为504 kN，此拉力直接传递给支座。图中虚线所围区域内，部分斜杆有较大的局部弯矩作用，其他部位的斜杆局部弯矩较小。

(2)环杆。网壳的环杆主要以受轴拉力为主，杆件862所受拉力最大，最大拉力178 kN;除与节点309连接的部分杆件有18 kN·m的局部弯矩外，其余部位的环杆局部弯矩较小。

(3)开口边界。网壳开口部位的杆件所受的轴压力和弯矩都较大，为压弯构件;其中杆件1002所受的内力最大，最大压力56 kN，最大弯矩46 kN·m。

2．2．2 方案改进

为降低结构在开口顶端的竖向位移，应增加结构在开口边界处的刚度，本工程采用如下两个加强方案(图6):

(1)方案1在开口边界处采用A325×16无缝钢管替换250×100方钢管。

(2)方案2将开口端前三跨斜杆所围区域内杆件壁厚由6 mm改为20 mm。

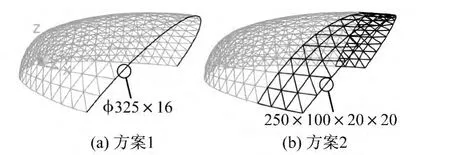
图6 结构加强方案Fig．6 Strengthening schemes

两个方案的计算分析结果和用钢量见表1。

表1 两个方案设计结果比较Table 1 Comparison of design results of two schemes

计算结果表明:两个方案的杆件设计最大应力比均小于0．6，最大节点位移均小于75 mm，采用单根边梁加强的方案1的用钢量为方案2的73．8%。

3 网壳稳定性分析

［2－8］中网壳稳定性的分析方法采用有限元软件ANSYS进行分析，网壳杆件采用BEAM188单元模拟，节点为刚接，采用固定铰支座。

3．1 线弹性屈曲分析

整体稳定分析的荷载工况采用恒荷载与活荷载(D+L)标准组合。结构的屈曲模态见图7，表2给出了D+L组合工况下，前6阶屈曲特征值与失稳形式。从表2和图7可知:

(1)两个方案对应阶数的屈曲模态相似，都是在前4阶为整体屈曲，到第5阶出现局部屈曲;

(2)除第1阶屈曲系数相近外，方案2的整体屈曲系数均小于方案1相应阶数，但由于方案2中对发生局部屈曲的杆件壁厚进行了加厚，其局部屈曲系数大于方案1相应阶数;

(3)两个方案在第5阶和第6阶出现的局部屈曲形状都是节点309(图5)及其连接的杆件向外凸起，为节点309的节点失稳。

表2 两个方案屈曲特征值与失稳形式Table 2 Buckling eigenvalue and unstability forms of two schemes

3．2 初始几何缺陷

本工程的初始缺陷采用一致缺陷模态法，考虑到施加初始缺陷后，最小特征值不一定发生在最低屈曲模态，因此本文对前6阶屈曲模态形式均进行了分析。初始缺陷的幅值参考《网格规程》［1］取为网壳跨度的l/300(l为网壳最大横向跨度)，本工程取用30 m/300=100 mm。计算结果见表3。

方案1中初始缺陷分布在整体双波反对称失稳的第4阶模态时，结构的几何非线性极限承载力最小，而方案2中初始缺陷分布在整体双波对称的第3阶时，结构的几何非线性极限承载力最小。进行结构整体稳定分析时，方案1的初始缺陷分布模式采用第4阶模态，方案2采用第3阶模态。

图7 两个方案的前6阶屈曲模态Fig．7 The first 6 buckling modes of two schemes

表3 两组截面非线性计算结果Table 3 Non-linear calculation results of two schemes

3．3 几何非线性分析

在D+L组合工况下，仅考虑几何非线性，缺陷幅值分别取 0，l/300，l/200，l/100，即 0，100 mm，150 mm，300 mm(l为结构最大横向跨度30 m)。图8(a)给出了结构在初始缺陷幅值为100 mm时方案1和方案2的整体稳定系数与节点竖向最大位移的关系曲线，图8(b)给出了不同初始缺陷幅值下的整体稳定系数。表4给出了不同初始缺陷幅值下的稳定系数。图9给出了缺陷幅值为100 mm时两个方案的结构几何非线性整体失稳的应力云图。

计算结果表明:

(1)在D+L组合工况下，仅考虑几何非线性时，方案1的稳定系数为21．3，方案2为23．9，均大于《网格规程》的推荐值4．2。

(2)从图8(b)中可以看出，随缺陷幅值的增加，网壳的稳定系数减小，但方案2的下降曲线比方案1的陡，初始缺陷对方案2的影响较方案1大。

(3)方案1在缺陷幅值为300 mm时的稳定系数为没有施加缺陷时稳定系数的86%，仅下降14%，对缺陷不敏感;方案2在缺陷幅值为300 mm时的稳定系数为没有施加缺陷时稳定系数的78%，下降22%。

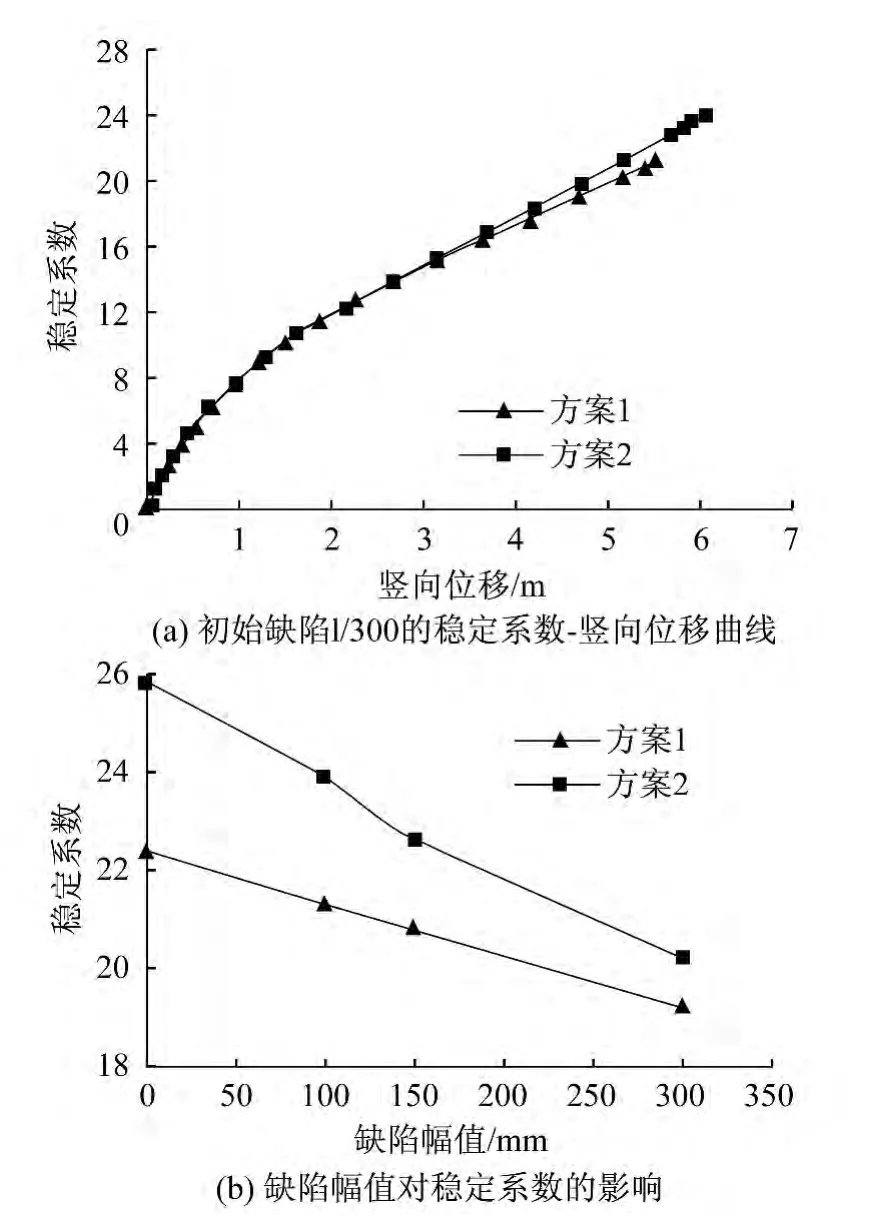
图8 几何非线性分析结果Fig．8 Geometric nonlinear analysis

3．4 几何、材料双非线性分析

由图9的应力云图可知，当达到几何非线性极限稳定时，最大应力已远远超过其钢材材料的屈服强度345 MPa，因此，必须考虑材料非线性影响。利用有限元软件ANSYS进行结构的双非线性分析，钢材本构关系假定为理想弹塑性，屈服强度 345 MPa，弹性模量 2．06 ×105MPa。

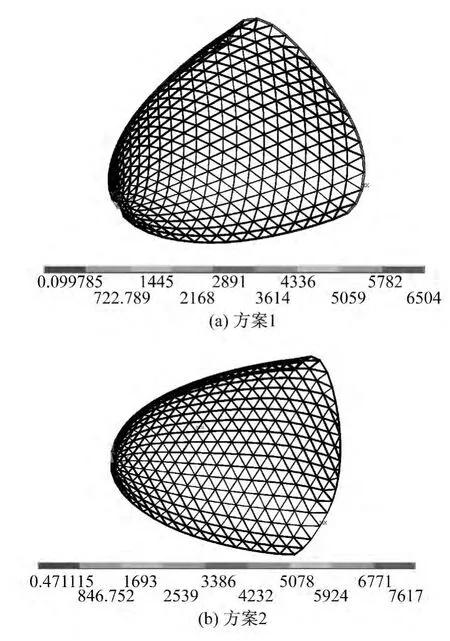
图9 几何非线性失稳应力云图(单位:MPa)Fig．9 Stress contour of geometric non-linear analysis

图10 (a)给出了结构在初始缺陷幅值为100 mm时方案1和方案2的双非线性整体稳定系数与节点竖向最大位移的关系曲线，图10(b)给出了不同初始缺陷幅值下的整体稳定系数。表4给出了不同初始缺陷幅值下结构双非线性的稳定系数。

由计算结果可见:

(1)方案1和方案2在D+L组合工况、缺陷幅值l/300时考虑几何、材料双非线性的整体稳定系数分别为5．01和5．98，大于《网格规程》的推荐值2．0，结构具有良好的稳定性能。

(2)方案1和方案2在缺陷幅值不同时，对应的双非线性稳定系数变化很小，两种组合的双非线性性能对缺陷都不敏感。

(3)在缺陷幅值l/300时，方案1的双非线性稳定系数仅为其几何非线性稳定系数的23%，方案2仅为25%，降幅都较大，说明材料非线性对结构的整体稳定承载力影响较大。

表4 两个方案稳定系数Table 4 Stability coefficients of two schemes

图10 几何、材料双非线性分析结果Fig．10 Geometric and material non-linear analysis

4 关键杆件失效对结构稳定的影响

4．1 关键杆件分析

由3．2节线弹性屈曲分析的结果知，方案1和方案2的第5阶、6阶屈曲模态都出现了节点309(图7)的节点失稳;由2．1节的静力分析也可知，结构在节点309附近的杆件所受的力也较其他部位杆件大，故需要考虑偶然情况下，节点309失效对结构整体稳定性的影响;此外，由于方案1中封边梁的截面承载力比杆件的承载力大很多，因此考虑封边梁部分失效对方案1结构整体稳定性的影响。

4．2 杆件失效时几何、材料双非线性稳定计算

分析在D+L工况组合作用下，不考虑初始缺陷时的结构几何、材料双非线性整体稳定性能。计算时，将失效杆件的钢材弹性模量改为2 MPa来模拟杆件失效;由于节点309失效后，与其连接的各杆件同时失效，故将与节点309连接的各杆件弹性模量改为2 MPa来模拟节点309失效;由2．1节静力分析可知，封边梁中杆件1002(图5)所受的内力较大，将杆件1002的弹性模量改为2 MPa，以模拟封边梁部分杆件失效。表5给出了方案1和方案2在部分杆件失效后结构考虑几何、材料双非线性时的稳定系数。

表5 两个方案杆件失效后稳定系数Table 5 Stability coefficients of two schemes after key members failure

由计算结果可知:

(1)因节点309失效，方案1稳定系数降低了75．2%，方案2降低了76．7%，节点309失效对两个方案的稳定性能影响很大，设计时应提高节点309及与其连接的各杆件的安全储备。

(2)因封边梁失效，方案1的稳定系数降低了13．4%，封边梁的部分失效对方案1的影响不大。

5 结论

通过以上分析，可以得出以下结论:

(1)开口网壳在开口处的变形较大，通过增设刚度较大的封边梁或加大开口边杆件的厚度都可以改善结构的变形能力。

(2)两个方案在D+L组合工况作用下，结构考虑几何非线性的稳定系数都大于4．2，结构考虑几何、材料双非线性的稳定系数都大于2．0，满足《空间网格结构技术规程》［1］要求，结构具有良好的整体稳定性;两个方案对初始缺陷不敏感。

(3)考虑材料非线性时，方案1和方案2的稳定系数较只考虑几何非线性稳定时分别降低了23%和26%，材料非线性对结构稳定性能有较大影响，设计时应加以考虑。

(4)节点309失效对结构稳定性影响较大，设计时因适当提高节点309及其连接杆件的安全储备;方案1中封边梁部分失效对结构的影响较小。

(5)两个方案的杆件应力比，节点最大位移以及稳定性能都满足《空间网格结构技术规程》［1］要求，但方案1的用钢量仅为方案2的73．7%，最终采用方案1进行结构设计。

参考文献

［1］ 中华人民共和国住房和城乡建设部．JGJ 7—2010空间网格结构技术规程［S］．北京:中国建筑工业出版社，2010．Ministry of housing and Urban ncral Devetopment of the People’s Republic of China．JGJ 7—2010 Technical specification for space frame structures［S］．Beijing:China Architecture and Building Press，2010．(in Chinese)

［2］ 曹正罡，孙瑛，范峰．肋环斜杆型球面网壳弹塑性稳定特性［J］．哈尔滨工业大学学报，2007，39(6):849-852．Cao Zhenggang，Sun Ying，Fan Feng．Elasto-plastic stability behavior of schwedler domes［J］．Journal of Harbin Institute of Technology，2007，39(6):849-852．(in Chinese)

［3］ 沈晓明，舒赣平．不规则划分单层网壳结构稳定性分析［J］．建筑结构，2009，39(4):101-104．Shen Xiaoming，Shu Ganping．Stability analysis of single layer lattice shell with irregular division［J］．Building Structure，2009，39(4):101-104．(in Chinese)

［4］ 朱庆华，崔鸿超，郑良知，等．“海南球”大跨度单层网壳结构设计［J］．建筑结构，2013，43(16):30-34．Zhu Qinghua，Cui Hongchao，Zheng Liangzhi，et al．Structural design on large span single layer lattice shell of Hainan ball［J］．Building Structure，2013，43(16):30-34．(in Chinese)

［5］ 孟美莉，孙璨，吴兵，等．深圳大运会篮球馆屋盖结构稳定性分析［J］．钢结构，2010，25(3):28-36．Meng Meili，Sun Can，Wu Bing，et al．Stability analysis of prestressing suspend dome of basketball center for universiade in Shenzhen［J］．Steel Construction，2010，25(3):28-36．(in Chinese)

［6］ 聂义田，李亚敏，王丽．单层球面网壳结构稳定性的双重非线性分析［J］．结构工程师，2013，29(4):57-62．Nie Yitian，Li Yaming，Wang Li．Non-linear stability analysis of single-layer truss shell structures［J］．Structural Engineers，2013，29(4):57-62．(in Chinese)

［7］ 郭远翔，黄慧隆．大跨度单层混合型球面网壳非线性稳定性研究［J］．结构工程师，2014，30(1):58-62．Guo Yuanxiang，Huang Huilong．Nonlinear stability analysis of a large span single-layer mixer spherical reticulated shell structure［J］．Structural Engineers，2014，30(1):58-62．(in Chinese)

［8］ 周谅，沈黎元．大庆石油会展中心椭球形单层网壳稳定分析［J］．结构工程师，2004，20(4):33-37．Zhou Liang，Shen Liyuan．Stability analysis of singlelayer oval reticulated shell of Daqing Exhibition Center［J］．Structural Engineers，2004，20(4):33-37．(in Chinese)