基于锥模型的非单调自适应信赖域算法
王开荣, 曾刘拴
(重庆大学 数学与统计学院, 重庆 401331)
基于锥模型的非单调自适应信赖域算法
王开荣, 曾刘拴*
(重庆大学 数学与统计学院, 重庆 401331)
针对无约束优化问题提出了一个基于锥模型的非单调信赖域算法.首先提出一种求解子问题的新方法,在此基础上给出该文算法.算法结合自适应技术,避免信赖域半径更新的盲目性;并引入滤子技术和新的非单调技术,利用非单调Armijo线搜索得到步长,进而产生新的迭代点.在一定的假设条件下,证明了该算法的全局收敛性,数值实验表明了算法的有效性.
无约束规划; 非单调信赖域算法; 自适应方法; 滤子; 全局收敛性
本文考虑无约束最优化问题:
(1)
其中,f(x):R→Rn二阶连续可微且有下界.
锥模型方法最初是由Davidon[1]和Sorensen[2]提出的.经典的锥模型如下:
(2)
其中,s=xk+1-xk,gk=f(xk),对称阵Bk∈Rn×n是2f(xk)或其近似,hk称为水平向量.若hk=0或者则锥模型退化为二次模型,因此锥模型是二次模型的推广,它包含更多的信息,具有二次模型没有的优势[3-5].
考虑到信赖域方法良好的性质,Di和Sun[6]首次提出了锥模型信赖域方法,他们考虑了下面的信赖域子问题:
(3)

近年来非单调线搜索技术[7-10]因其较好的数值效果而得到了广泛应用.2008年Mo和Gu[11]提出了一种较为简单的非单调技术,即:
f(xk+αsk)≤Dk+δαf(xk)Tsk,
(4)
其中,
(5)
并将此技术运用到信赖域方法中,获得了较好的数值效果.
自适应方法[12-14]可以避免信赖域半径更新的盲目性.2009年,Sang和Sun[15]充分利用当前迭代点的信息提出了一种自适应方法,即令
(6)
其中,
(7)
0<ω1<ω2<1, 0 滤子技术[16]最初的目的是为了克服使用价值函数时选取罚因子的困难.2005年,Gould等[17]将滤子技术应用到一般的无约束优化问题中,提出了一个滤子信赖域方法,2012年,孙文瑜和徐东[18]提出了一种基于锥模型的滤子信赖域方法,证明了其收敛性,并得到较理想的数值效果. 为了给出求解(3)的简单算法,首先简化子问题(3),在第k步迭代中,用χ(xk)I来逼近Bk,则子问题(3)转化为下面的形式: (8) 另外,锥模型应该满足下面的四个插值条件[5]: ck(0)=fk,ck(0)=gk, (9) ck(-sk-1)=fk-1,ck(-sk-1)=gk-1, (10) 其中,sk-1=xk-xk-1,由(10)的第一个等式可得 (11) (12) 因此有 (13) 若χ(xk)≤0,则选取充分小的常数δ1>0,令 (14) 这样就可以保证Bk=χ(xk)I正定. 锥模型函数ck(s)的严格极小点为: (15) 求解问题(3)的计算步骤为: 算法1 有了算法1,就可以给出求解问题(1)的算法2如下: 算法2(FNTR) (16) 的最小的非负整数,令αk=λik,xk+1=xk+αksk. 其中, 转第2步骤. 对算法2的收敛性,首先给出以下假设: (H1)f(x)在有界闭集H={x|f(x)≤f(x0)}上二阶连续可微; (H2) 算法2产生的序列包含在H中; 证明由Bk+1=χ(xk+1)I和说明(1)很容易得到. 引理2[20]若假设(H1)、(H2)、(H3)成立,sk是子问题(8)的解,则有 (17) 引理4若{xk}是由算法2产生的,则对任意的k有 fk+1≤Dk+1≤Dk (18) 证明由Dk的定义知Dk+1-fk+1=η(Dk-fk+1). 现在考虑3种情况:k∈T,k∈S,k∈A. 第1种情况:k∈T. 所以Dk+1-fk+1=η(Dk-fk+1)>0,即Dk+1>fk+1,又因 Dk+1-Dk=(η-1)Dk+(1-η)fk+1= (1-η)(fk+1-Dk)≤0, 即有Dk+1≤Dk,所以当k∈T时结论成立. 第2种情况:k∈S. 由滤子的定义知fk+1≤fk.若k-1∈T,则有fk≤Dk≤Dk-1,从而有 Dk+1=ηDk+(1-η)fk+1≤ ηDk-1+(1-η)fk=Dk, 即Dk+1≤Dk,又因 Dk+1-fk+1=η(Dk-fk+1)≥ η(fk-fk+1)≥0, 即fk+1≤Dk+1,所以有fk+1≤Dk+1≤Dk. 若k-1∈S,令M={i|1 下面用数学归纳法证明Dk+1≤Dk. 因f0=D0,所以k=1时有 D1=ηD0+(1-η)f1≤ ηf0+(1-η)f0=f0=D0. 假设k=n时,有Dn+1≤Dn下证k=n+1时有Dn+2≤Dn+1,而 Dn+2=ηDn+1+(1-η)fn+2≤ ηDn+(1-η)fn+1=Dn+1, 所以Dk+1≤Dk成立. 再证fk+1≤Dk+1,因Dk+1-Dk=(η-1)Dk+(1-η)fk+1=(1-η)(fk+1-Dk),而由上面的证明可知Dk+1≤Dk,又(1-η)>0 ,所以有(fk+1-Dk)≤0,即fk+1≤Dk,从而有 Dk+1=ηDk+(1-η)fk+1≥ ηfk+1+(1-η)fk+1=fk+1. 如果M≠Φ,设m=min{i|i∈M},则有fk+1≤fk≤…≤fk-m+1,因k-m∈T,由第一种情况可知fk-m+1≤Dk-m+1≤Dk-m,而 Dk-m+2=ηDk-m+1+(1-η)fk-m+2≤ ηDk-m+(1-η)fk-m+1=Dk-m+1, 由归纳法可得Dk+1≤Dk,同上可得fk+1≤Dk+1. 综上可得当k∈S时,有fk+1≤Dk+1≤Dk. 第3种情况:k∈A. 即Dk>fk+1,所以Dk+1-fk+1=η(Dk-fk+1)>0, 即Dk+1>fk+1,而 Dk+1-Dk=(η-1)Dk+(1-η)fk+1= (1-η)(fk+1-Dk)<0, 则有Dk+1≤Dk, 所以有fk+1≤Dk+1≤Dk. 综合上面3种情况可知,对任意的k都有fk+1≤Dk+1≤Dk. 引理5若假设(H1)、(H2)、(H3)成立,则存在常数M>0,使得对任意的k有 (19) 证明由假设(H1)可知gk和2f(x)是一致有界的,即分别存在Mg>0和Mf>0使得对任意的k有和再由Taylor展式可得: (20) (21) 因fk有界,故Dk有界,所以有 (22) (23) 由引理4知{Dk}单调下降,又{Dk}有界,故其收敛,再由引理3和引理6得 又由Dk+m+1的定义知Dk+m+1是fk+1,fk+2,…,fk+m+1的凸组合,因此有 定理4若假设(H1)、(H2)、(H3)成立,算法2产生的点列{xk}收敛于x*,2f(x*)正定,2f(x)在x*的邻域内Lipschitz连续,其中,Lipschitz常数为L,如果有 (24) (25) 0 从而 又 所以 因此 表1 检验函数对应编号 表2 算法2(FNTR)和算法(TR)、算法(FilterTR)、算法(CRFTR)的数值结果 续表2 从表2的数据可以看出,算法2(FNTR)与算法(TR)相比,对于函数Penalty Ⅰ,Penalty Ⅱ,Variably,Broyden tridiagonal的高维情况,后者失效,且对于函数Broyden banded,后者无法求解,而算法2(FNTR)在这些函数上都有出色的表现,说明算法2(FNTR)的构造是可行的.算法2(FNTR)与算法(FilterTR)相比,对于函数Box 3-D,Osborne 2,Penalty Ⅰ,Penalty Ⅱ和Broyden banded,后者基本上无法求解,对于函数Variably,Broyden tridiagonal和Linear full rank的高维情况,后者基本失效,而前者却可以很好的求解,并且在其它函数的数值表现上,算法2(FNTR)也有很大的优势,说明对于大多数测试函数,锥模型与滤子方法的结合在数值表现上具有优势.算法2(FNTR)与算法(CRFTR)相比,在函数Gaussian,Box 3-D,Osborne 2,Penalty Ⅰ,Penalty Ⅱ的数值表现上,前者具有明显的优势,在函数Jensam,Gulf,Discrete integral,Broyden tridiagonal,Linear full rank的数值表现上,两者同样优秀,而在函数Variably, Broyden banded的数值表现上,前者稍显不足,说明在在信赖域方法框架下,线搜索、锥模型、非单调、自适应以及滤子等技术是可以混合使用的.上述结果表明本文提出的算法2(FNTR)是可靠有效的. [1] Davidon W C. Conic approximation and collinear scaling for optimizers[J]. SIAM Journal on Numerical Analysis, 1980, 17:268-281. [2] Sorensen D C.The Q-superlinear convergence of a collinear scaling algorithm for unconstrained optimization [J].SIAM Journal on Numerical Analysis, 1980, 17:84-114. [3] Ni Q. Optimization conditions for trust-region subproblems involving a conic model [J]. SIAM J Optim, 2005, 15:826- 837. [4] Qu Shaojian, Jiang Suda.A trust-region method with a conic model for unconstrained optimization[J].Math Meth Appl Sci, 2008, 31:1780-1808. [5] Sun W Y, Yuan Y X.Optimization Theory and Methods[M]. New York:Springer, 2006. [6] Di S S. Stregion method for conic model to solve unconstrained optimization [J]. Optim Methods Softw, 1996, 6:237-263. [7] Grippo L, Lampariello F, Lucidi S. A nonmonotone line search technique for Newton’s method[J].SIAM Journal on Numerical Analysis, 1986, 23(4) :707-716. [8] Deng N Y, Xiao Y, Zhou F J. Nonmonotone trust region algorithm[J]. Journal of Optimization Theory and Applications,1993, 76 (2) :259-285. [9] Zhang H, Hager W W. A nonmonotone line search technique and its application to unconstrained optimization[J].SIAM Journal on Optimization, 2004, 14(4):1043-1056. [10] Mo J, Liu C, Yan S. A nonmonotone trust region method based on nonincreasing technique of weighted average of the successive function values[J].Journal of Computational and Applied Mathematics, 2007, 209(1):97-108. [11] Gu Nengzhu, Mo Jiangtao.Incorporating nonmonotone strategies into the trust region method for unconstrained optimization[J].Computers and Mathematics with Applications, 2008, 55(9):2158-2172. [12] Sartenaer A. Automatic determination of an initial trust-region in nonlinear programming [J]. SIAM Journal on Scientific Computing, 1997, 18(6):1788-1803. [13] Fan J Y, Yuan Y X. A new trust region algorithm with trustregion radius converging to zero[C]//Proceedings of the 5th International Conference on Optimization:Techniquesand Applications,Hongkong, Dec, 2001. [14] Zhang X S, Zhang J L, Liao L Z. An adaptive trust method and its convergence [J].Computers and Mathematics with Applications, 2003, 45(10-11):1469-1477. [15] Sang Zhaoyang, Sun Qingying. A self-adaptive trust region method with line search based on a simple subproblem model[J].Journal of Computational and Applied Mathematics, 2009, 232(2):514-522. [16] Fletcher R,Leyffer S. Nonlinear programming without a penalty function [J].Mathematical Programming, 2002, 91(2):239-269. [17] Gould N I M, Sainvitu C. Toint P H L.A filter-trust-region method for constrained optimization[J].SIAM Journal on Optimization, 2005, 16(2):341-357. [18] 孙文瑜, 徐 东. 解无约束最优化的基于锥模型的过滤集-信赖域方法[J].中国科学, 2012, 42(5):527-543. [19] 诸梅芳, 薛 毅, 张凤圣. 锥模型的拟NEWTON型信赖域方法[J].高等学校计算学报, 1995, 17:36-47. [20] Qu Shaojian, Zhang Kecun, Zhang Jian. A nonmonotone trust-region method of conic model for unconstrained optimization[J]. Journal of Computational and Applied Mathematics. 2008, 220:119-128. [21] 冯 琳, 段复建, 和文龙. 基于简单二次函数模型的滤子非单调信赖域方法[J].山东大学学报:理学版, 2012(5):1-8. [22] 袁亚湘, 孙文瑜. 最优化理论与方法[M].北京:科学出版社, 1997. [23] 繆卫华, 孙文瑜. 一个解无约束优化问题的过滤信赖域方法[J].高等学校计算数学学报, 2007, 29(1):88-96. [24] 葛恒武. 无约束优化问题的锥模型回溯过滤信赖域算法[J].苏州大学学报:自然科学版, 2010, 26(2):8-11. [25] More J J, Garbow B S, Hillstrom K E. Testing uncontrained optimization software[J]. ACM Trans Math Softw, 1981, 7(1):136-140. Nonmonotone adaptive trust-region algorithm with a conic model for unconstrained optimization WANG Kairong, ZENG Liushuan (College of Mathematics and Statistics, Chongqing University, Chongqing 401331) A non-monotone filter trust-region algorithm is proposed based on a conic model for solving unconstrained optimization. Firstly, a new method for solving the sub-problem is proposed in this paper; then a new algorithm is put forwarded. In the algorithm, a self-adaptive technology is employed to avoid the blind updating of the trust region radius; a filter-set technique and a new non-monotone technique is also introduced,and then a step size is obtained making use of non-monotone Armijo line search rule,thus a new iterative point is achieved. The global convergence of this new algorithm is shown under certain conditions. Finally, the numerical experiments are carried out to demonstrate the effect of our algorithm. unconstrained optimization; nonmonotone trust-region algorithm; self-adaptive; filter; global convergence 2014-06-27. 重庆市高等教育教学改革研究项目(102104). 1000-1190(2015)02-0171-08 O221.2 A *通讯联系人. E-mail: zengliushuanxi@163.com.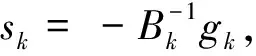
1 基于锥模型的非单调滤子自适应信赖域算法





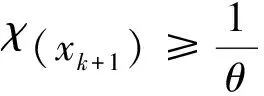














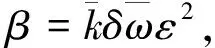

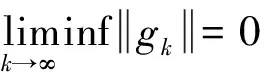





2 数值试验





3 结束语

