椭球体放矿理论移动过渡方程的重构
郭进平 刘 东 李荣福
(西安建筑科技大学材料与矿资学院,陕西 西安 710055)
椭球体放矿理论移动过渡方程的重构
郭进平 刘 东 李荣福
(西安建筑科技大学材料与矿资学院,陕西 西安 710055)
介绍了放矿理论的移动过渡方程,指出椭球体放矿理论的密度场假设违背连续介质假说的根本前提,论证了基于现有的密度场假设的椭球体放矿理论移动过渡方程的缺陷,重构了新的移动过渡方程,进一步完善了椭球体放矿理论的基础。
椭球体 放矿理论 密度场 移动过渡方程
移动过渡方程是放矿理论的基础方程,不少放矿理论的速度方程、移动方程都是根据移动过渡方程建立起来的[1-6],移动过渡方程是否正确,成为放矿理论成败的关键之一。
如图1所示,当放出放出体Qf时,放出前的移动体Q0移动过渡为移动体Q,移动过渡方程就是反映Q0、Qf、Q三者关系的方程。
1 放矿理论的移动过渡方程[2]
对于散体,无论平均二次松散系数η=1或η>1,根据质量守恒定律,均有
(1)
式中,Qf为放出体体积;Q0为放出前移动体初始体积;Q为放出Qf时Q0移动体的体积;ρa为放出前移动体(散体)初始密度;ρCQ为移动体Q内平均密度。
式(1)为散体移动的质量平衡方程,是移动过渡的基础方程,根据这个基础方程,可进一步建立移动过渡方程。
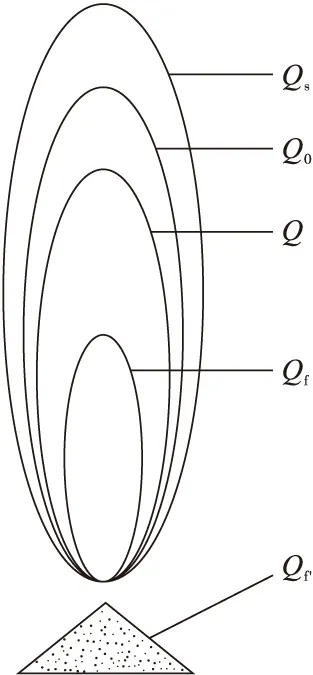
图1 散体放出过程
放矿理论中出现了2个移动过渡方程,分别介绍如下。
1.1 类椭球体放矿理论的移动过渡方程[1,3]
类椭球体理论只承认在理想散体(η=1)条件下的移动过渡方程,没有提出和研究实际散体(η>1)的移动过渡方程。
当η=1时,密度场为均匀场和定常场,散体中移动范围内的颗粒都在放矿开始时同时投入运动,场内各点的密度均相等,即有
(2)
式中,ρ为放出时移动体内任一点的密度;ρ0为放出体放出密度。
将式(2)代入式(1),得
(3)
式(3)为η=1时移动过渡方程的体积表达式。
1.2 椭球体理论的移动过渡方程[2,4]
椭球体理论假设散体场的二次松散是在移动边界上一次完成的,松动带内各处的密度相等为平均密度ρC,Q0内的所有颗粒一开始放出就同时投入运动。在此假设基础上建立了椭球体理论的移动过渡方程。
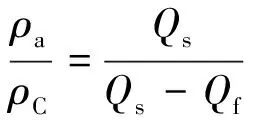
(4)
或
(5)
式(4)或式(5)是在η>1条件下建立起来的椭球体理论的移动过渡方程。显然,椭球体理论对散体密度均匀的假设是椭球体理论的移动过渡方程成立的基础。
下面对椭球体理论移动过渡方程建立的前提条件及方程本身谈点认识。
2 椭球体理论密度场假设的缺陷
散体在放出前其密度场比较简单,可以认为各处密度相同,且不随时间变化,属于均匀场、定常场。散体放出后,静止带密度场保持原有的状态,仍然是均匀场、定常场,而移动带内的密度则随空间位置和时间的变化而变化,密度场变成了非均匀场和不定常场[5]。
移动带内散体密度的变化是复杂的,在散体二次松动时散体颗粒除正常移动外还会出现压实、空洞、脉冲塌落或移动等现象,但是从总体上看,统计平均值表明,密度变化还是可以看成连续的、有规律的。实验观察表明:放出体的垂线方向,离放出口越近密度越小,离移动边界越近,密度越大。水平径向方向,离放出口轴线越近,密度越小,离移动边界越近,密度越大。在进行放矿理论研究时,应舍弃压实、空洞、脉冲等现象,注重统计平均值的描述,注意连续、有规律变化的特点,这是将散体作为连续介质研究的基础[5]。
椭球体理论设计了一个密度场,在移动范围内,该密度场的密度各处都相同且等于移动范围内的平均密度[1]。
二次松散是在移动边界上一次完成,即在移动边界上由初始密度瞬时变为平均密度。同样经平均二次松散的散体的再松散也是在放出口一次瞬时完成的,即在放出口由移动场内各处均为平均密度变为放出密度[2]。
这个密度变化假说的主要问题是[4]:
(1)与实际不符。我们观察到的实际散体在移动带内的密度都是各处不同的,而且随时间变化,也就是说设计的这个密度场是没有根据的、是想象的。
这与我们假设了一个η=1的各处密度都相同的理想散体的密度场不同,理想散体密度场是假设散体无限放出时,无限趋近的密度场,不是瞬时形成的密度场。
(2)违背散体是连续介质的假设。根据连续介质假设,散体是连续的、散体中各处的速度、密度等物理量也必须是连续的、可导的、无间断点、有确定值。椭球体放矿理论,假定在移动边界上和放出口一次完成密度变化,使放出口(无论理论还是实际放出口)和移动边界上的点成为间断点、无确定的密度值(或者说同时存在2个值),而移动边界是变化的,就是说散体场中各处都有一次成为间断点、无确定值的“机会”。因此,这个假设的密度场违背了连续介质理论基础。
综上所述,椭球体放矿理论的移动过渡方程建立的基础是值得商榷的。
3 椭球体放矿理论移动过渡方程的缺陷
椭球体放矿理论移动过渡方程除了是建立在一个有问题的密度场假说的基础上,移动过渡方程本身也存在以下问题。
(1)椭球体放矿理论移动过渡方程表明,散体场中的颗粒是放出一开始就全部同时投入运动的,即假想所有颗粒按平均二次松散系数松散膨胀到新位置而后同时投入运动。这是不符合实际的,由于密度的变化(二次松散的存在),散体场中的散体颗粒是逐渐投入运动的,即存在运动滞后现象,至于松散膨胀更是脱离实际。
(4)椭球体放矿理论移动过渡方程表明,该方程没有区分质量守恒和移动过渡的区别,或者说方程将在保持质量守恒条件下的移动体Q0内尚未投入运动的颗粒都看作移动颗粒了。事实上,移动过渡一定要有位置的变化、是一个渐进的过程,不包括也不研究移动体Q0内尚未投入运动的颗粒。
以上分析都说明,现有的椭球体放矿理论移动过渡方程没有反映颗粒移动的情况,不符合实际,作为近似计算可以理解,但作为放矿理论的基础方程是欠妥的。
4 椭球体放矿理论移动过渡方程的重构
由椭球体放矿理论的密度场的讨论可知,移动过渡方程建立的基础在实际和理论方面都存在问题,下面来建立椭球体放矿理论新的移动过渡方程。
首先要说明的是我们不去解决椭球体放矿理论密度场的问题(类椭球体放矿理论已经解决了),而是在承认原有椭球体理论密度场假设的基础上,重构新的移动过渡方程,解决现有移动过渡方程不反映移动滞后的问题。无论密度场如何都必须重构,因为原有的移动过渡方程建立过程欠妥。
对于实际散体(η>1),散体场中的颗粒不是放出一开始所有的颗粒都投入运动的,而是随着放出体体积的增加逐渐投入运动,也就是说有一个运动滞后问题,Q0表面颗粒这种滞后关系可用式(6)来表示:
(6)

将式(6)代入式(1),整理得
(7)

椭球体理论认为松动带内密度都为平均密度ρC,且认为ρCQ=ρC(当η>1时,ρCQ≠ρC),式(7)除以ρC得
(8)

但我们认为,作为质量平衡方程研究是成立的,但作为移动过程研究是不可取的,因为质量多少与运动状态无关,而移动过程与运动状态密切相关。既然是移动过渡方程,哪怕是从方程推导得出的结果相同(如速度方程),也不是代替真正移动过渡关系(方程)的理由。因为现有移动过渡方程用平均状态来描述移动过渡关系没有反映真正的移动过程,特别是移动滞后过程。
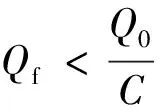
可以看出,重构的椭球体放矿理论的移动过渡方程基础扎实,物理意义明确,放矿过程描述清楚,符合实际,进一步丰富和完善了椭球体放矿理论基础。
5 结 论
(1)类椭球体理论承认理想散体(η=1)的移动过渡方程Q0-Qf=Q,该方程是从质量守恒定律推导出来的,方程是正确的。
(2)椭球体放矿理论假设的密度场与实际不符,违背连续介质假说,是造成移动过渡方程出现问题的重要原因。
(3)椭球体放矿理论对移动过程的研究是含混不清的,没研究散体场中颗粒滞后投入运动这一状态。
(4)椭球体理论现有的移动过渡方程ηQ0-ηQf=Q是不完善的,与实际移动过程不符。
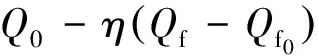
(6)新建立的移动过渡方程物理意义明确,放矿过程描述清楚,符合实际。
[1] 刘兴国.放矿理论基础[M].北京:冶金工业出版社,1995. Liu Xingguo.Basic Drawing Theory[M].Beijing:Metallurgical Industry Press,1995.
[2] 李荣福.类椭球体放矿理论的理想方程[J].有色金属:矿山部分,1994(5):38-44. Li Rongfu.The ideal equation of quasi-ellipsoid drawing theory [J].Nonferrous Metals:Mine Section,1994(5):38-44.
[3] 李荣福.放矿基本规律的统一数学方程[J].有色金属:矿山部分,1983(1):1-8. Li Rongfu.The unified mathematical equation of ore drawing of the basic law[J].Nonferrous Metals:Mine Section,1983(1):1-8.
[4] 李荣福.椭球体放矿理论的几个主要问题——椭球体放矿理论建立的必要性[J].中国钼业,1994(5):39-43. Li Rongfu.Several main problems of ellipsoid drawing theory:The necessity of establishing quasi-ellipsoid drawing theory[J].China Molybdenum Industry,1994(5):39-43.
[5] 李荣福,张慎河.连续介质放矿理论的检验(上)[J].金属矿山,2000(6):8-13. Li Rongfu,Zhang Shenhe.Verification of the drawing theory in the continuous medium(Ⅰ)[J].Metal Mine,2000(6):8-13.
[6] 李荣福,张慎河.连续介质放矿理论的检验(下)[J].金属矿山,2000(8):15-19. Li Rongfu,Zhang Shenhe.Verification of the drawing theory in the continuous medium(Ⅱ)[J].Metal Mine,2000(8):15-19.
(责任编辑 石海林)
Reconstruction of Moving Transition Equation for Ellipsoid Drawing Theory
Guo Jinping Liu Dong Li Rongfu
(SchoolofMaterialsandMineralResources,Xi'anUniversityofArchitectureandTechnology,Xi'an710055,China)
The moving transition equation of drawing theory is introduced.It is pointed out that the assumption of density field on ellipsoid drawing theory violates the fundamental premise of the continuous medium hypothesis.The defects of moving transition equation of ellipsoid drawing theory based on existing density field assumption are demonstrated.Also,a new moving transition equation is constructed to further improve the foundation of ellipsoid drawing theory.
Ellipsoid,Drawing theory,Density field,Moving transition equation
2015-06-02
教育部高等学校博士学科点专项科研基金项目(编号:2012120110017),西安建筑科技大学重点培育学科建设基金项目(XK201205)。
郭进平(1970—),男,副教授,硕士研究生导师。
TD853.36
A
1001-1250(2015)-10-037-04

