岩体强度空间变异性与边坡可靠性研究

任富强 常 远 常来山 陈东伟

(1. 中国矿业大学（北京）力学与建筑工程学院，北京100083;2. 深部岩土力学与地下工程国家重点实验室，北京100083;3. 辽宁科技大学矿业工程学院，辽宁 鞍山114051)

以往对边坡的可靠性分析中，岩体一般是作为均质的随机介质考虑，认为不同点间的岩体强度参数是一致的，这显然是不符合实际的，实际的岩土介质不同点间、整体和局部的强度参数都有一定的差异性，这就需要考虑岩体的空间变异性，其中Vanmarcke［1-2］在该理论方面进行了开创性研究，随后Chowdhurry［3］利用随机场理论描述了岩体性质的空间变异性。地质统计学理论被广泛应用于岩体空间变异性的评估，其中王家臣等［4-7］用地质统计学理论中的变差函数经过推导得出岩体性质参数的相关距离和相关函数，说明了岩体性质的空间变异性，并进行了考虑岩体空间变异性的边坡可靠性分析，但只考虑了1 种理论变差函数模型。

本研究结合野外实测点荷载数据拟合出了理论变差函数的球状模型、高斯模型和指数模型的相应曲线，并利用蒙特卡洛抽样方法结合理论变差函数模型对单一岩性的边坡岩体进行了可靠性分析。

1 岩体强度的空间变异性

1.1 现场点荷载测试

为了得到岩体强度的空间分布特征，在某露天铁矿的某一勘探剖面上垂直岩层走向方向以间距1 m等间距布置46 个测点。在每个测点上利用SD －1型数码点荷载仪对选取的若干混合岩岩块进行了点荷载实验，将实测结果按ISRM 法并经过尺寸修正计算得到标准点荷载强度指数Is(50)，其垂直于岩层走向分布情况如图1 所示。由图1 可知，在空间位置上，标准点荷载强度指数Is(50)有较大的差异，但其整体较为稳定，未曾发生漂移。对实测的数据进行统计分析后得出其平均值为11.60 MPa，标准差为6.79 MPa，变异系数为0.585。

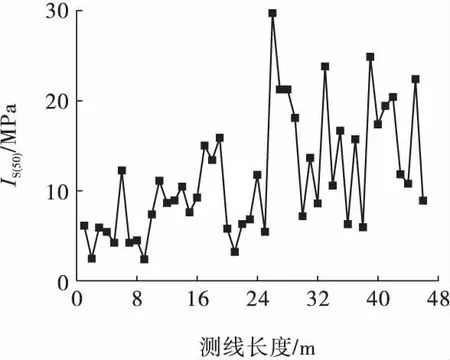
图1 混合岩Is(50)垂直岩层走向分布情况Fig.1 The vertical strata distribution of migmatite Is(50)

1.2 实验变差函数与理论变差函数

混合岩Is(50)为区域化的变量且满足二阶平稳假设，故可按地质统计学中的实验变差函数［8-10］来计算Is(50)的实验变差函数值r(h)，即

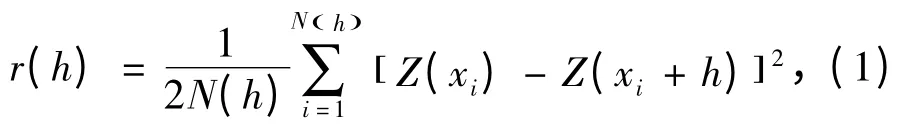
式中，h 为取样点的间隔距离，取1 m;N(h)为被h 相隔的数据对的数目;Z(xi)和Z(xi+h)在此为Is(50)的不同取值。

为了预估区域化的变量Is(50)的未知值，需要根据实验变差函数值拟合成相应的理论变差函数模型，其中球状模型、高斯模型和指数模型的理论公式分列如下。

(1)球状模型:

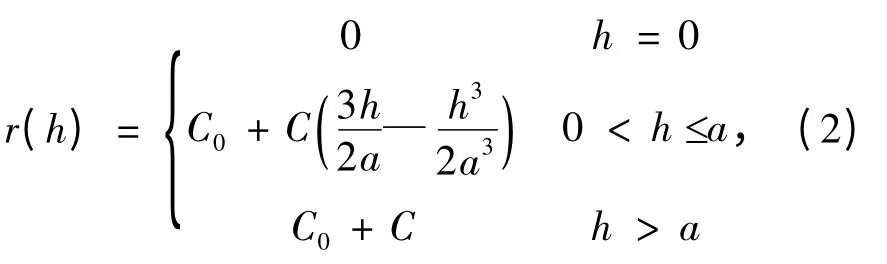
式中，C0为块金常数;C0+ C 为基台值;C 为拱高;a为变程(即随机场中的相关距离D)。

(2)高斯模型:

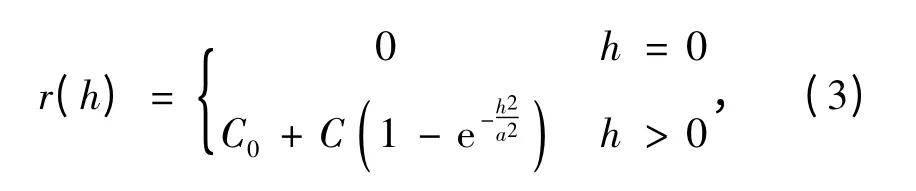
(3)指数模型:

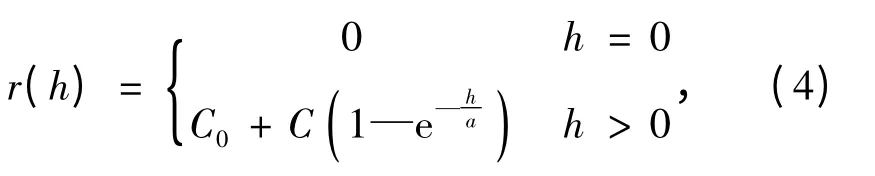
式中，a 不是变程，变程为3a，即h =3a 时，r(h)≈C0+C。

采用上述理论变差函数模型中的球状模型、高斯模型和指数模型，根据实验变差函数曲线利用Visual Basic 进行最小二乘拟合，拟合后3 个理论变差函数模型的参数见表1。由表1 可知指数模型相关距离最大，高斯模型的最小，由相关距离的物理含义可知同等长度内指数模型的数据点的相关性最大，高斯模型最小;此外指数模型与高斯模型的基台值相同，略大于球状模型的基台值，可近似认为3 种模型描述的Is(50)在垂直于岩层走向方向上变化幅度大小相同。实验变差函数曲线与理论变差函数曲线如图2 所示，由图2 可知3 种模型的拟合曲线的趋势一致，且对应的拟合值基本相同。

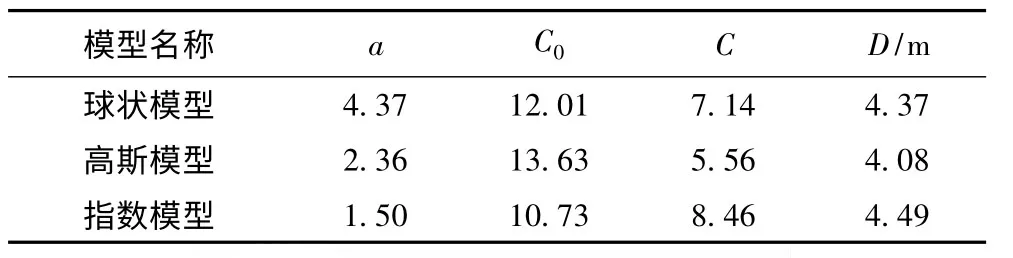
表1 混合岩Is(50)计算结果Table 1 The calculation result of migmatite Is(50)

图2 混合岩3 种模型实验与理论变差函数曲线Fig.2 Curves of three kinds of model experiment and theoretic variation function for migmatite

1.3 岩体强度局部分析

由理论变差函数，可以求出岩体强度的相关函数。根据岩体强度，相关函数的定义为

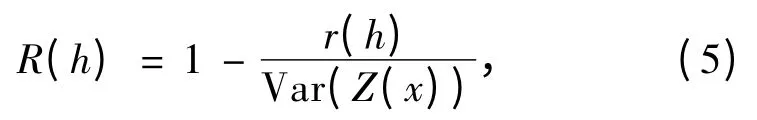
式中，R(h)为强度相关函数;r(h)为理论变差函数;Var(Z(x))为Is(50)的方差，混合岩的方差为46.043。

根据式(5)可以得到混合岩3 种模型对应的R(h)，而在边坡可靠性计算中一般要将岩体分条再将每一分条作为均质体处理，在每一分条上岩体强度要局部平均化，在二阶平稳假设的前提下局部平均化后的期望与整体的期望相同，但方差要发生变化。根据局部平均域大小、强度的空间相关距离、相关函数等不同，其方差衰减的程度不同，一般用式(6)表示岩体强度局部平均化后的方差，式中ZT(x)表示平均域长度为T 的岩体强度函数，G(T)为方差衰减函数，可由式(7)计算。故可以得到混合岩3 种模型对应的方差衰减函数以及方差函数。

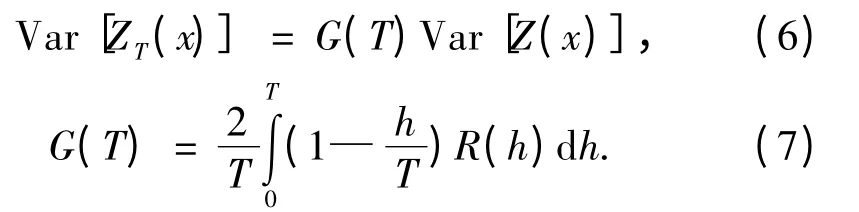
2 边坡可靠性分析

为方便对比分析，探讨不同的变差函数模型对边坡可靠性的影响规律，构造了图3 所示的均质混合岩的简单边坡模型，边坡高度为400 m，边坡角为45°。

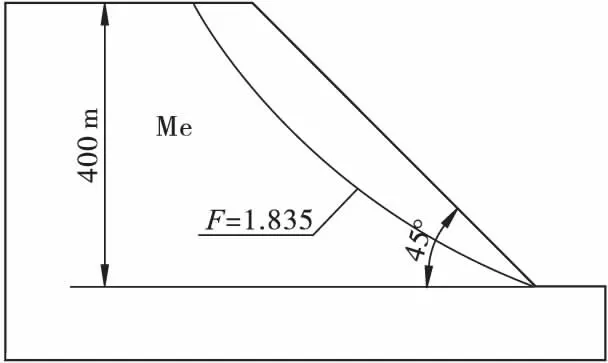
图3 混合岩简单边坡模型Fig.3 The simple slope model of migmatite

应用Monte－Calo 随机抽样技术［11-12］，通过Visual Basic 编程得到岩体强度参数的随机分布特征，模型的计算参数如表2 所示。极限平衡计算选用毕肖普(BISHOP)法，用单纯形变法［13］进行优化计算，确定了危险滑弧及安全系数，危险滑弧如图3 曲线所示，混合岩边坡的安全系数F 为1.835。

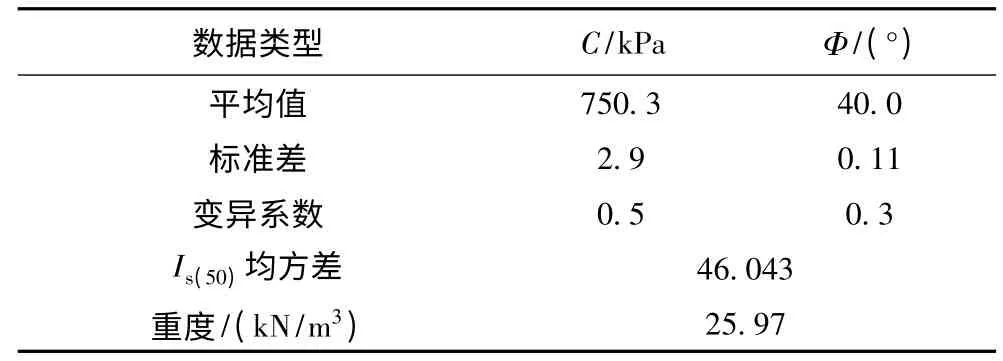
表2 岩体强度参数随机分布表Table 2 The random distribution of rock strength parameters

根据不同的分条宽度将球状模型、高斯模型、指数模型的可靠性指标［14］的部分计算结果列于表3 所示。

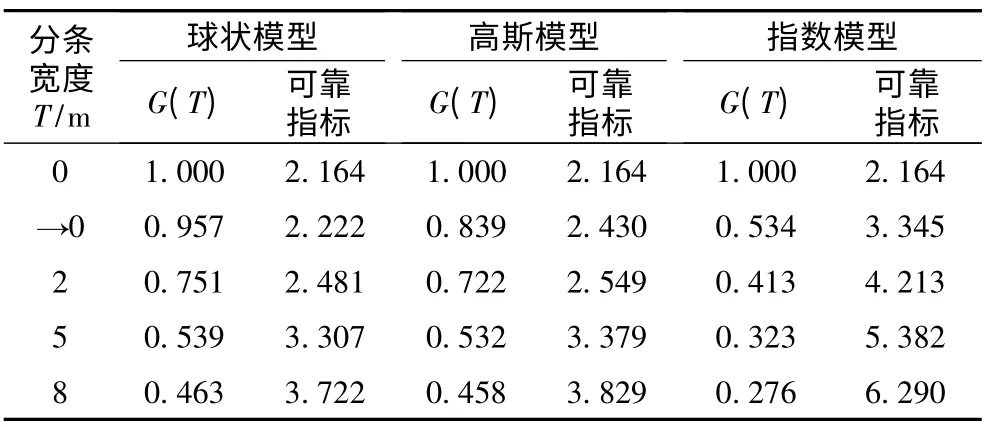
表3 混合岩边坡Monte-Calo 法部分计算结果Table 3 Parts of calculation result by Monte-Calo method for migmatite slope

由表3 比较混合岩球状模型、高斯模型、指数模型的边坡可靠性指标计算结果。若以球状模型为基准，高斯模型的绝对差值为0.003 ～0.312，平均为0.053，相对差值为0.515% ～17.154%，平均为3.383%;指数模型的绝对差值为0.046 ～2.568，平均为1.141，相对差值为11.348% ～83.229%，平均为59.941%;指数模型相差的较多，可靠性计算结果偏高，而高斯模型与球状模型的可靠性计算结果较为接近。将3 种模型的可靠指标随分条宽度变化的关系曲线绘制如图4 所示。

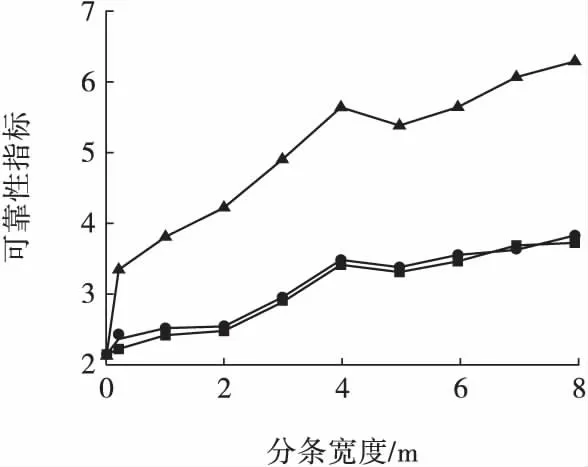
图4 3 种模型可靠性指标对比Fig.4 The reliability index contrast of three kinds of model

由图4 可知，在分条宽度T =0 即不考虑岩体强度空间变异性时与T 趋于0 时有一个落差，并且差值的大小与块金常数C0有关。不考虑岩体强度的空间变异性时边坡的可靠指标最小，随分条宽度的增加可靠指标整体呈增大的趋势，其中球状模型与球状模型趋势基本一致都低于指数模型的增长趋势。当分条宽度大于相关距离时3 种模型的可靠指标均有下降的趋势直到达到一定的分条宽度时又逐渐随分条宽度的增大而上升。

3 结 论

(1)高斯模型的相关距离最小，指数模型的最大，3 种模型描述的岩体强度沿垂直于岩层走向方向的变化幅度基本接近。

(2)当考虑岩体强度空间变异性时计算边坡的可靠指标增加，破坏概率降低。主要是由于强度参数方差衰减所致，而且在分条宽度达到相关距离前随分条宽度的增加而增大，分条宽度达到相关距离之后的可靠指标先减小后增大。

(3)球状模型与高斯模型的可靠指标随分条宽度的变化基本一致，整体值都低于指数模型的可靠指标，增加的趋势也较指数模型平缓。

［1］ Vanmarke E H. Random Fields:Analysis and Synthesis［M］.［S.l.］:The MIT Press，1983.

［2］ Vanmarke E H. Probabilistic stability analysis of earth slopes［J］.Eng Geology，1980，16(1):29-50.

［3］ Chowdhurry R N.Simulation of risk of progressive slope failure［J］.Can Geotech J，1992，29(1):94-102.

［4］ 谭文辉，王家臣，周汝弟.岩体强度参数空间变异性分析［J］.岩石力学与工程学报，1999，18(5):497-502.

Tan Wenhui，Wang Jiachen，Zhou Rudi.Analysis on spatial variability of strength parameter of rock mass［J］. Chinese Journal of Rock Mechanics and Engineering，1999，18(5):497-502.

［5］ 谭文辉，蔡美峰，周汝弟.岩体空间变异性对边坡可靠性的影响研究［J］.工程力学，2001(S):517-521.

Tan Wenhui，Cai Meifeng，Zhou Rudi.Influence of spatial variability of rock mass on the slope reliability research［J］. Engineering Mechanics，2001(S):517-521.

［6］ 王家臣，王艳青，宁 柯.应用地质统计学研究岩体强度的空间变异性［J］.黄金科学技术，1999，7(45):51-54.

Wang Jiacheng，Wang Yanqing，Ning Ke.Application of geostatistics study spatial variation of rock mass strength［J］. Gold Science and Technology，1999，7(45):51-54.

［7］ 王家臣，谭文辉，宁 柯.义马北露天煤矿工作帮边坡可靠性研究［J］.岩土工程学报，2000，22(1):105-108.

Wang Jiachen，Tan Wenhui，Ning Ke.The reliability research on the working slope of North Surface Coal Mine of Yima Coal Administration［J］. Chinese Journal of Geotechnical Engineering，2000，22(1):105-108.

［8］ 王仁铎，胡光道.线性地质统计学［M］.北京:地质出版社，1988.

Wang Renduo，Hu Guangdao.Linear Geostatistics［M］.Beijing:Geological Press，1988.

［9］ 张仁铎.空间变异理论及应用［M］.北京:科学出版社，2006.

Zhang Renduo. Spatial Variation Theory and Application［M］. Beijing:Science Press，2006.

［10］ 李章林，王 平，李冬梅.实验变差函数计算方法的研究与运用［J］.国土资源信息化，2008，8(2):10-14.

Li Zhanglin，Wang Ping，Li Dongmei. Research and application of the method calculating experiment variogram［J］. Land and Resources Informatization，2008，8(2):10-14.

［11］ 李育超，凌道盛，陈云敏，等.蒙特卡洛法与有限元相结合分析边坡稳定性［J］. 岩石力学与工程学报，2005，24(11):1933-1941.

Li Yuchao，Ling Daosheng，Chen Yunmin，et al. Slope stability analysis using monte carlo technique with FEM［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(11):1933-1941.

［12］ 李 亮，褚雪松，袁长丰，等.快速蒙特卡罗法及其在土坡可靠度分析中的应用［J］.煤炭学报，2013，38(9):1576-1582.

Li Liang，Chu Xuesong，Yuan Changfeng，et al. Fast Monte-Carlo method and its application in the soil slope reliability analysis［J］.Journal of China Coal Society，2013，38(9):1576-1582.

［13］ 燕子宗，费浦生，万仲平. 线性规划的单纯形法及其发展［J］.计算数学，2007，29(1):121-127.

Yan Zizong，Fei Pusheng，Wan Zhongping.Classical simplex methods for linear programming and their develppments［J］.Mathematica Numerica Sinica，2007，29(1):121-127.

［14］ 张昀青，李维珍，闫静昌，等.边坡可靠性指标及敏感性因素分析［J］.石家庄铁道大学学报:自然科学版，2015，28(1):62-65.

Zhang Yunqing，Li Weizhen，Yan Jingchang，et al.The slope reliability index and sensitivity factor analysis［J］.Journal of Shijiazhuang Railway Institute:Natural Science，2015，28(1):62-65.