不同地质条件下的采场结构参数优化

羊羽翔 付建新 宋卫东

(北京科技大学土木与环境工程学院，北京 100083)

不同地质条件下的采场结构参数优化

羊羽翔 付建新 宋卫东

(北京科技大学土木与环境工程学院，北京 100083)

为了确定不同地质条件下较为合理的采场结构参数，采用理论计算与数值模拟相结合的方法，对不同矿岩稳定性条件下的采场跨度进行选择与优化。以程潮铁矿西区作为研究的工程背景，采用简支梁理论、矿房宽度计算公式对合理跨度与临界跨度进行了计算，并通过FLAC3D数值模拟软件对不同跨度参数的采场稳定性进行了分析。结果表明：矿岩条件为稳固、中等稳固、稳固性较差时的矿房合理跨度分别为18.87、14.93、8.08 m。多矿房回采，位移及拉应力的最大值通常出现在区域中间部位，且矿房跨度的增加极易引起开采区域最大沉降值的迅速增加。矿柱顶板沉降值对矿房跨度也非常敏感。数值模拟结果与理论计算值相符，这表明数值模拟能很好地反映地下开采的真实状态，为采场结构参数确定提供依据。

采场跨度 数值模拟 地质条件 最小主应力 塑性区

对于矿山实际回采工作而言，合理的采场参数需根据不同矿山的不同开采条件来确定，但即使在同一矿山的开采范围内，也存在着不尽相同的地质条件，因此同一矿山不同开采区域内的采场参数也不能一概而论。合理的采场参数有利于提高采矿效率，而采场参数过大则会带来安全隐患。

针对采场合理跨度的选择前人做了很多研究，在合理跨度的理论计算方面，结构力学和材料力学中的梁理论[1]将采区看作岩梁，计算时将其简化为平面弹性力学问题，从而可以计算出采场最大允许的跨度。根据普通房柱法矿房宽度的计算公式[2]也能算出矿房的合理宽度。

在数值模拟实际开采的研究中，主要使用的方法有有限单元法、离散单元法以及有限差分法等等。唐巨鹏等人[3]通过ansys软件建立煤矿的开采模型，计算了地表沉陷曲线和最大沉陷位置，指出了随开采推进沉陷位移和影响范围。付建新等人[4-7]通过FLAC3D软件模拟了矿山回采过程，分析了开采过程中的地压问题，确定了合理的采场布置及开采顺序。

本研究以程潮铁矿西区作为研究的工程背景，在已有矿岩稳定性分级的成果上，考虑将程潮西区矿岩体划分为好、一般、较差3种分类，并分别进行矿房矿柱合理跨度的设计。首先运用简支梁理论以及矿房宽度计算公式计算得出不同地质条件下矿房矿柱的最大允许跨度，接着运用FLAC3D数值模拟软件分析采区内的拉应力、顶板位移以及塑性区分布的情况，对所选定的采场参数进行优化，以理论力学研究与数值模拟分析相结合的方式，确定程潮铁矿西区不同地质条件下适宜的采场跨度参数。

1 采场允许跨度理论分析

1.1 矿区概况及及矿岩稳定性评价

程潮铁矿是国内特大型的金属矿山，在-500 m水平以上采用分段高度17.5 m，进路间距15 m的无底柱分段崩落法进行开采，在转入-500 m以下开采后考虑采用分段空场嗣后充填法进行开采，在使用充填法试采的5采场中，采用了矿房宽度13 m，矿柱宽度7 m的采场布置参数，由于矿柱较窄而开采形成的空区较大，出现了地压显现，锚喷支护层出现开裂、脱落等不安全现象。因此确定合适的采场参数显得尤为重要，将直接影响到采矿的效率与安全。

RMR分类方法主要以岩体的单轴抗压强度、岩芯质量指标RQD值、节理间距、节理条件、地下水情况等5个指标作为评判的依据，将岩体划分为非常好的岩体、好岩体、一般岩体、不好的岩体、非常不好的岩体5类，程潮铁矿各岩体的具体分类情况见表1。

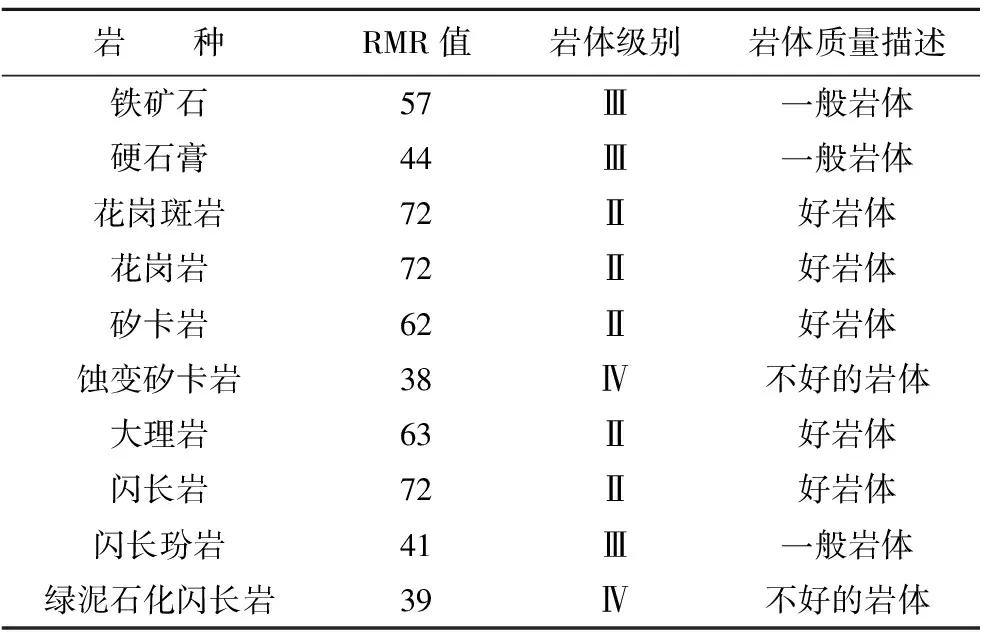
表1 主要矿岩稳定性分类结果

由表1可知，总体围岩处在中等稳固到稳固，对于具体矿段应根据实际情况分析。

1.2 不同地质条件下采场跨度理论计算

由地质条件的分析可知西区矿石的稳固性较好，上下盘围岩的稳固性有一定差别。根据这些岩性分级的情况，考虑设计3个方案对不同矿岩稳定性条件及采场结构参数条件下的采场围岩破坏情况进行研究。方案Ⅰ为矿体稳固，上下盘围岩稳固性较差，考虑上下盘围岩为蚀变矽卡岩、绿泥石化闪长岩。方案Ⅱ为矿体稳固，上下盘中等稳固，考虑上下盘岩体为铁矿石、硬石膏、闪长玢岩。方案Ⅲ为矿体与上下盘围岩都稳固，考虑上下盘围岩为闪长岩、花岗岩、大理岩等。各方案的力学参数如表2所示。

表2 各方案力学参数

1.2.1 简支梁理论

场顶板可假设为两端简支梁，根据材料力学，岩梁中性轴上、下表面上任意一点的应力为

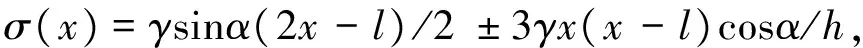
(1)

式中，α为矿体倾角，(°)；l为岩梁跨度，m；h为岩梁高度，m；γ为岩体容重，kN/m3。

最大拉应力发生在x=L/2+htanα/6处岩梁中性轴的下表面，最大拉应力为

(2)

因此，顶板倾向的最大允许跨度为

(3)

顶板垂直走向的最大允许跨度为

(4)

式中,σt为岩体抗拉强度。

1.2.2 合理矿房矿柱宽度计算

对于阶段空场嗣后充填法开采的采场，根据采场回采的安全保障及生产能力，可以确定矿房的宽度。在采场安全得到保障的情况下，矿房的宽度和高度越大，采场的生产能力也越大。矿房宽度计算式如下：

(5)

以方案Ⅲ为例，将H=500 m，γ=26.2 kN/m3，σt=4.1MPa代入式(5)中，可得阶段嗣后充填采场的矿房宽度为L=18.87m。

由于矿柱相应参数一致，故矿柱合理宽度与矿房一致。

1.2.3 计算结果

将各方案的参数分别代入式(4)和式(5)，各方案的最大允许跨度见表3。

表3 各方案允许的空场跨度

从表3中可以看出，简支梁理论所计算的结果是相应矿岩条件下的最大允许跨度，因而结果偏大，在实际应用中应以合理矿房宽度的计算结果为参考，最大不能超过简支梁理论的计算结果。

2 采场跨度数值模拟分析优化

2.1 数值模拟方案设计与采场建模

为了研究不同采场结构参数条件下采场围岩的破坏情况，验证理论计算的合理性，且考虑到程潮西区大部分的矿岩条件与方案Ⅱ接近，故在方案Ⅱ的基础上对应设计了3种数值模拟方案：方案1，矿房、矿柱宽度均为8 m；方案2，矿房矿柱宽度均为15 m；方案3，矿房、矿柱宽度均为18 m。

数值模拟的力学参数取值如表4所示。

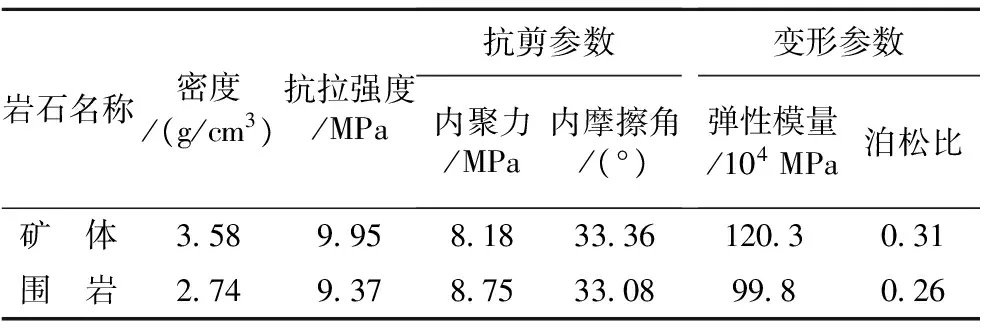
表4 数值模拟力学参数取值

模型示意图如图1所示。本次模拟计算选取了3个矿房开采作为模拟对象，根据矿山生产的实际开采流程(图1中1～9)，一个矿房开采结束并充填完毕后再进行下一个矿房的开采，同水平3个矿房依次开采，通过数值模拟分析围岩的应力、位移、塑性区变化规律。

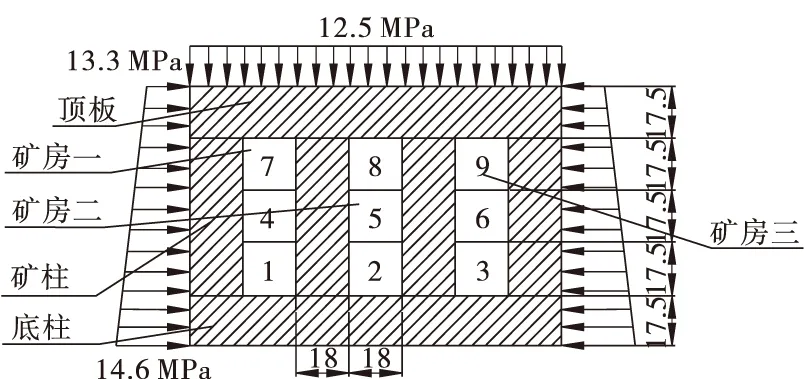
图1 回采顺序(单位：m)

2.2 采场稳定性分析

由图2可知，开采结束后，矿房二监测点沉降值最大，而两侧的矿房一和三则相差较小。进行拟合可知，随着开采的进行，矿房二监测点沉降值呈指数增加，而两侧的矿房一和三则呈现线性增加。从图2中可以看出，多矿房回采，最终最大值通常出现在区域中间部位，且矿房跨度的增加极易引起开采区域最大沉降值的迅速增加。

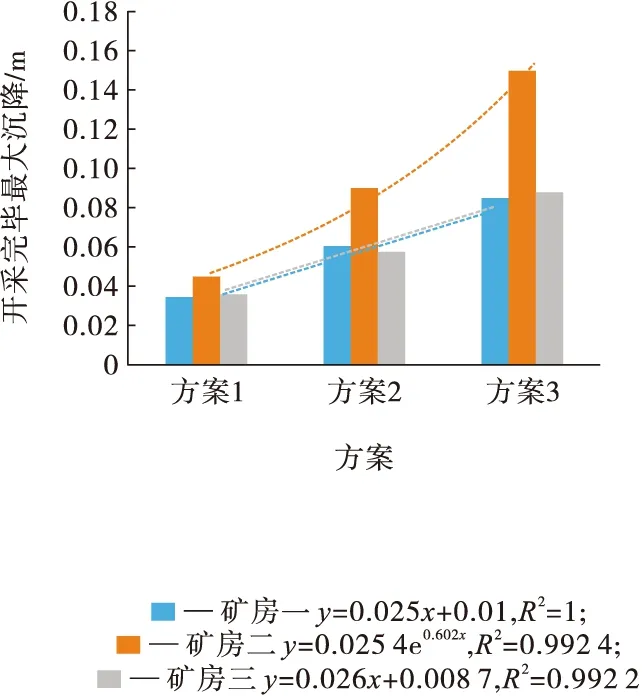
图2 各方案矿房最大沉降值

由图3可知，矿柱顶板沉降值对矿房跨度非常敏感，随着开采的进行，不同方案矿柱顶板监测点位移均呈指数增加，且矿柱二位移偏大。

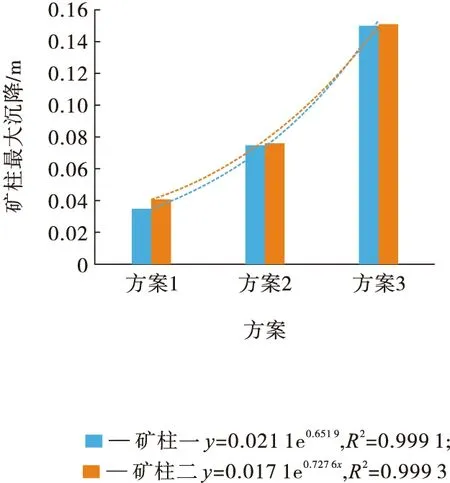
图3 各方案矿柱最大沉降值

由岩体的力学性质可知，岩体通常的抗拉强度比其抗压强度要小许多，因此在最大主应力小于其抗压强度的情况下主要考虑其最小主应力中是否出现了拉应力。图4为不同开采方案结束后，3个矿房顶板最小主应力条形图及其拟合曲线。由图4可知，随着跨度的增加，3个矿房顶板均出现了拉应力，且随跨度增加而变大，不同区域的矿房增加规律不同，中间区域的矿房二则呈对数增加，两侧则呈多项式增加。对比可知，方案2中，矿房三的拉应力最小，说明此时对围岩扰动规律较小。综合来看，方案1最小主应力没有明显增加，之后开始出现较大程度增加。

由图5可知，随着跨度的增加，3个矿房开采并充填结束后中间矿柱处在塑性区的比例也就越大，即矿柱破坏也就越严重，最终回采并充填完毕后，围岩的塑性区也就越大，尤其是开采区域的上方。图5显示，方案1仅仅出现少量塑性区，方案2塑性区比方案1有所增加，而方案3矿柱中破坏区域大大增加，出现了塑性区贯通的破坏状态，造成后面回采矿柱时难度大大增加，因此不宜采用。

图4 各方案顶板拉应力值

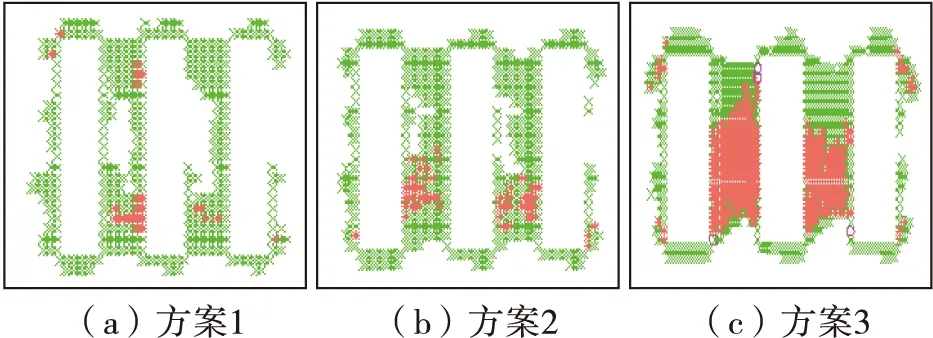
图5 各方案塑性区示意

综合方案1、2及3，考虑程潮西区大部分区域矿岩稳定性较好，属于方案Ⅱ所描述的地质类型，最终确定方案2为最优方案，符合理论计算的结果。现场可根据实际地质情况，灵活调整参数，但最大不宜超过18 m。

3 结 论

(1)通过程潮西区矿岩稳定性分级结果将矿区地质条件归纳为3种方案，并根据简支梁理论与矿房宽度计算公式计算了各方案的矿房最大允许跨度以及合理跨度。矿岩条件稳固时矿房合理跨度为18.87 m，最大允许跨度为30.22 m；矿岩条件中等稳固时矿房合理跨度为14.93 m，最大允许跨度为26.93 m；矿岩条件稳固性较差时矿房合理跨度为8.08 m，最大允许跨度为15.93 m。

(2)从数值模拟的结果来看，多矿房回采，最终位移的最大值以及拉应力的最大值通常出现在区域中间部位，且矿房跨度的增加极易引起开采区域最大沉降值的迅速增加。矿柱顶板沉降值对矿房跨度也非常敏感。由塑性区可知，随着矿房跨度的增加，塑性区也不断增加，直至方案3矿柱中破坏区域出现了塑性区贯通的破坏状态，说明方案3不宜采用。

(3)对比数值模拟与理论计算的结果可知，方案3矿房跨度18 m过大，产生了塑性区贯通破坏，而方案1矿房跨度8 m则影响实际生产的效率与开采成本，15 m的矿房跨度即方案2为3个方案中的最优方案，这与理论计算的合理跨度14.93 m相符。

(4)数值模拟相对于理论计算考虑的因素更多，结果更加直观，而理论计算则可以确定计算结果的大方向，使数值计算的结果不至于偏离实际，因此理论计算结合数值模拟来确定矿块参数提高了结果的可信度，更加接近工程实际。

[1] 张海波，宋卫东，付建新.大跨度空区顶板失稳临界参数及稳定性分析[J].采矿与安全工程学报，2014，31(1)：66-71. Zhang Haibo，Song Weidong，Fu Jianxin.Analysis of large-span goaf roof instability critical parameters and stability[J].Journal of Mining & Safety Engineering，2014，31(1)：66-71.

[2] 邢兆超，卜祥才.近地表铁矿床采矿方法和矿房结构参数的确定[J].山东冶金，2013，35(4)：14-15. Xing Zhaochao，Bu Xiangcai.Determination of mining methods and stope structure parameters for near-surface iron deposit[J].Shandong Metallurgy，2013，35(4)：14-15.

[3] 唐巨鹏，潘一山.ANSYS 在煤矿开采数值模拟中应用研究[J].岩土力学，2004(S2)：329-332. Tang Jupeng，Pan Yishan.Application of ANSYS software to numerical simulation of coal mining[J].Rock and Soil Mechanics，2004(S2)：329-332.

[4] 宋卫东，杜建华，尹小鹏，等.金属矿山崩落法开采顶板围岩崩落机理与塌陷规律[J].煤炭学报，2010，35(7)：1078-1083. Song Weidong，Du Jianhua，Yin Xiaopeng，et al.Caving mechanism of hanging wall rock and rules of surface subsidence due to no-pillar sub-level caving method in an iron mine[J].Journal of China Coal Society，2010，35(7)：1078-1083.

[5] 徐文彬，宋卫东，谭玉叶，等.金属矿山阶段嗣后充填采场空区破坏机理[J].煤炭学报，2012，37(S1):53-58. Xu Wenbin，Song Weidong,Tan Yuye，et al.Failure mechanism of stope and exploited areas with stage backfill method in metal mine[J].Journal of China Coal Society，2012，37(S1):53-58.

[6] 宋卫东，付建新，王东旭.露天转地下开采围岩破坏规律的物理与数值模拟研究[J].煤炭学报，2012，37(2)：186-191. Song Weidong，Fu Jianxin，Wang Dongxu.Study on physical and numerical simulation of failure laws of wall rock due to transformation from open-pit to underground mining[J].Journal of China Coal Society，2012，37(2)：186-191.

[7] 徐文彬，宋卫东，杜建华，等.崩落法转阶段充填法采场稳定性分析[J].北京科技大学学报，2013，35(4)：415-422. Xu Wenbin，Song Weidong，Du Jianhua，et al.Stability analysis of a backfill stope due to transforming from block caving t o stage backfill[J].Journal of University of Science and Technology Beijing，2013，35(4)：415-422.

(责任编辑 石海林)

Stope Structural Parameter Optimization under Different Geological Conditions

Yang Yuxiang Fu Jianxin Song Weidong

(SchoolofCivilandEnvironmentalEngineering，UniversityofScienceandTechnologyBeijing，Beijing100083，China)

In order to determine the more reasonable stope structural parameters under different geological conditions,theoretical calculation and numerical simulation methods are adopted to select and optimize the stope width under different stability.With the western area of Chengchao Iron Mine as engineering background,the simply supported beam theory and the stope width calculation formula are used to calculate out the reasonable span and the critical span.And the stope stability under different stope width was analyzed by FLAC3Dsoftware.The results indicated that when rock keeps stable,moderately stable or less stable,the reasonable stope width needs to be 18.87 m,14.93 m and 8.08 m separately.In multi-stope mining,maximum displacement and tensile stress usually occurs in the middle of the area,and the increase of stope span can easily cause a rapid increase of maximum displacement.The subsidence of pillar roof also greatly impacted the stope span.The simulation results were consistent with the theoretical value,which indicates that the numerical simulation can well reflect the real state of underground mining,and provide the basis for determining stope structural parameters.

Stope width，Numerical simulation，Geological condition，Minimum principle stress，Plastic zone

2015-07-28

国家自然科学基金项目(编号：51274023， 51374033)。

羊羽翔(1991—)，男,硕士研究生。通讯作者 宋卫东(1966—)，男，教授，博士研究生导师。

TD853

A

1001-1250(2015)-10-029-04