多点爆破震动速度衰减规律研究

刘建坡 许宏亮 王少泉 程崇强 荆洪迪

(1.深部金属矿山安全开采教育部重点实验室，辽宁 沈阳 110819;2.中冶北方工程技术有限公司，辽宁 大连 116600)

多点爆破震动速度衰减规律研究

刘建坡1许宏亮2王少泉2程崇强2荆洪迪1

(1.深部金属矿山安全开采教育部重点实验室，辽宁 沈阳 110819;2.中冶北方工程技术有限公司，辽宁 大连 116600)

爆破震动是引起地下矿山巷道破坏的重要原因，掌握爆破震动速度衰减规律，降低爆破震动危害，对矿山的安全高效生产有着重要意义。针对铁蛋山矿区爆破震动造成下盘沿脉运输巷道破坏严重的现状，开展了爆破震动监测工作。对于完整爆破信号数据，采用最小比例距离方法确定了多点爆破爆心距、炸药量和最大振速值的对应关系，为萨道夫斯基公式应用提供参数，并采用实例验证了该方法的可靠性。在此基础上，建立了铁蛋山矿区爆破震动速度衰减模型，获得了距离下盘沿脉运输巷道不同位置开采时所允许的最大单段药量。对矿山回采过程中的爆破参数进行了改进，不同区域采用不同最大单段药量，保证了沿脉运输巷道的稳定性和产能需求。

爆破震动 振速衰减 多点爆破 萨道夫斯基公式 安全控制

爆破是矿山生产主要环节之一，其质量的好坏不仅威胁到矿山工作人员和建筑结构的安全，而且影响着矿山生产过程中的铲装、运输、机械破碎等后续工艺的效率和经济效益。生产爆破震动是引起地下矿山巷道破坏的重要原因，当爆破引起巷道所处地带的震动幅值大于一定的数值时，会引起巷道的损坏。因此，掌握爆破震动波的传播规律，建立合理的爆破安全判据，针对具体的矿山工程提出有效降低爆破震动危害的措施，对矿山的安全高效生产有着重要意义。

在对爆破地震效应研究的过程中，大量的测试资料和工程实践表明，地面质点震动速度与建(构)筑物破坏的相关性最好，因此，各国都逐渐采用质点震动速度作为衡量爆破震动强度的物理量。其中，萨道夫斯基经验公式作为爆破震动参数衰减方程的应用最为普遍。国内外研究针对萨道夫斯基经验公式中的相关参数K、α的取值、适用情况和工程应用开展了广泛的研究，并取得了诸多有益的成果。但是在萨道夫斯基经验公式应用中，爆破位置是作为一个点(坐标唯一)来进行考虑的，即不管是单段爆破还是多段爆破，爆破位置距离监测点的距离是唯一的。对于多点爆破(多个位置同时起爆或者近似同时起爆)的情况研究较少。

本研究以辽宁北票保国铁矿铁蛋山矿区为工程背景，针对其爆破震动造成下盘沿脉运输巷道破坏严重的现状，开展爆破震动监测，采用萨道夫斯基经验公式对多点爆破情况下的爆破震动速度衰减规律进行了研究，对矿山现有爆破参数所引起的爆破震动速度进行了安全评价，为矿山的爆破参数优化提供依据，保障矿山安全生产。

1 爆破震动测试方案

保国铁矿铁蛋山矿区位于辽宁北票境内，矿体总体走向呈近SN向，厚度从几米到数百米不等，倾角50°～65°，2007年开始转为地下开采，目前矿山年产铁矿石近200万t，主要采用无底柱分段崩落法进行开采。回采进路垂直矿体走向布置，炸药采用乳化粒状铵油炸药，用FZY-1装药器装药。爆破采用导爆索和导爆管双能源起爆。

铁蛋山矿段矿体为磁铁石英岩矿层，属坚硬和半坚硬岩石，稳定性较好。上盘围岩主要为混合岩，局部夹斜长角闪岩，下盘围岩主要为混合岩，均为前震旦系建平群中深变质岩系。下盘围岩破碎松软，稳定性差，具有抗压强度低、变形大、来压快、遇水极易膨胀产生变形破坏等特点，导致其矿山沿脉运输巷道的稳定性问题十分突出。因此，开展爆破震动测试，研究爆破震动对围岩、巷道稳定性的影响是十分必要的。

结合现场工程布置，在铁蛋山矿+35 m和+20 m水平开采爆破震动测试工作，每个水平各布置3个测点，共6个测点，如图1所示。测试所采用设备为四川拓普测控科技有限公司生产的NUBOX-6016型智能震动监测仪，并配套TP3V-4.5 三维速度型传感器。在综合考虑现场因素以及不妨碍矿山生产顺利进行的情况下，开挖巷道底板至基岩，浇筑混凝土形成水泥台面以便传感器安装。每次爆破前1 h，使用速凝石膏来固定传感器在水泥台面上，并采用防护措施保护好设备以防止被爆破冲击波损坏。本次测试工作于2014年4月、5月开展，共开展了15次爆破测试。

2 多点爆破信号分析方法

萨道夫斯基公式给出了爆破震动速度随炸药量和爆心距等因素之间的定量关系。该方法具有明确意义，应用方便，为爆破设计提供了理论依据，是目前爆破工程中应用最为广泛的方法，其关系式如下：

图1 巷道工程布置及爆破震动测试方案

(1)

式中，V为质点震动速度，cm/s；Q为单段最大炸药量，kg；R为观测点到爆源的距离，m；K为与介质性质相关的系数；α是震动波随距离衰减的系数。

应用萨道夫斯基公式进行计算时，爆破位置可以看作1个点，爆源与测点之间的距离R是唯一的。对于单段爆破，取总药量Q进行计算。当采用多分段微差爆破时，取最大单段药量Q进行计算。对于保国铁矿铁蛋山矿区来说，每天下午15:30左右在多个进路进行爆破，每个进路爆破1排炮孔(每排11～12个炮孔)，每排炮孔同时起爆，不同进路之间采用分段微差起爆。这种情况下，每个爆破位置距离测点的距离是不同的，存在多个爆心距R1，R2，R3，…，Rn，对应不同的炸药使用量Q1，Q2，Q3，…，Qn(图2)。这种情况下，判断某个信号来自哪个爆源困难很大，因而无法采用萨道夫斯基公式进行爆破安全评价。

针对上述问题，采用比例距离Rm对爆破信号进行分析，比例距离Rm定义为

图2 爆破信号传播示意

(2)

依据《爆破安全规程》，K取值为正，α取值大于1。依据公式(1)，比例距离Rm越小，所产生的质点震动速度越大。因此，可分别计算出不同爆破位置的比例距离Rm，以最小比例距离Rm，min所对应的爆心距R、炸药量Q和最大振速值V来进行萨道夫斯基公式计算。为验证该方法的可靠性，本研究进行了实例分析。

表1、表2和图3分别为5月13日+35 m水平爆破位置、炸药使用量、测点3获得的爆破振速和波形图。此次爆破共有3个进路位置分段爆破，分别为+35 m水平8#进路、9#进路和11#进路，炸药量分别为485、556和545 kg，比例距离分别为10.22 、9.87和8.46 m/kg1/3。测点3处的测试设备完整地记录了该3段爆破信号，其质点震动速度分别为3.658 m/s，1.213 m/s和6.05 m/s。该3段爆破中比例最小的爆破所对应的质点震动速度最大。

表1 5月13日+35 m水平爆破数据

表2 5月13日测点3爆破振速统计

Table 2 Blast vibration velocity at measurestation 3 on May 13

cm/s

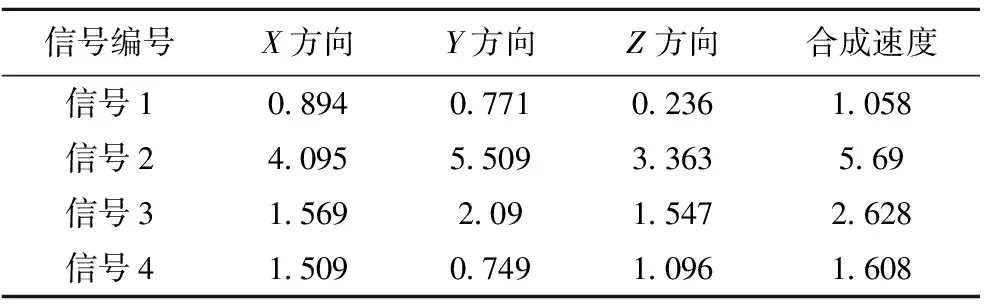
5月21日+35 m水平爆破位置、炸药使用量、测点5的爆破振速和波形图见表3、表4和图4。从中可以看出，11#进路爆破所对应的比例距离最小，为6.99 m/kg1/3，在测点5处所产生的质点震动速度最大，为5.69 m/s。限于篇幅，其他验证实例在此不做赘述。

图3 5月13日爆破信号波形图

爆破点距 离/m炸药量/kg比例距离/(m/kg1/3)8#进路788956095711#进路570654569913#进路8474561102723#进路19269291974

表4 5月21日测点5爆破振速统计

Table 4 Blast vibration velocity at measurestation 5 on May 21

cm/s

图4 5月21日爆破信号波形图

值得注意的是，采用最小比例距离Rm，min来判断最大振速对应起爆点的方法只适用于信号不丢失或不叠加的情况。对于由设备灵敏度低或爆破震动信号衰减所造成的信号缺失情况，或者由于信号叠加造成的信号减少的情况，该方法并不适用。因此，遇到测点所检测到的信号数量少于爆源数量时，应剔除该数据，选择信号不丢失或不叠加的数据进行计算分析。

3 爆破震动速度衰减模型及数据分析

本次测试工作于2014年4月和5月开展，共开展了15次爆破测试。现场每天在+35m水平和+50m水平各进行1次分段爆破。通过最小比例距离Rm，min获得萨道夫斯基公式计算参数的方法，共得到60组有效数据，部分数据见表5。

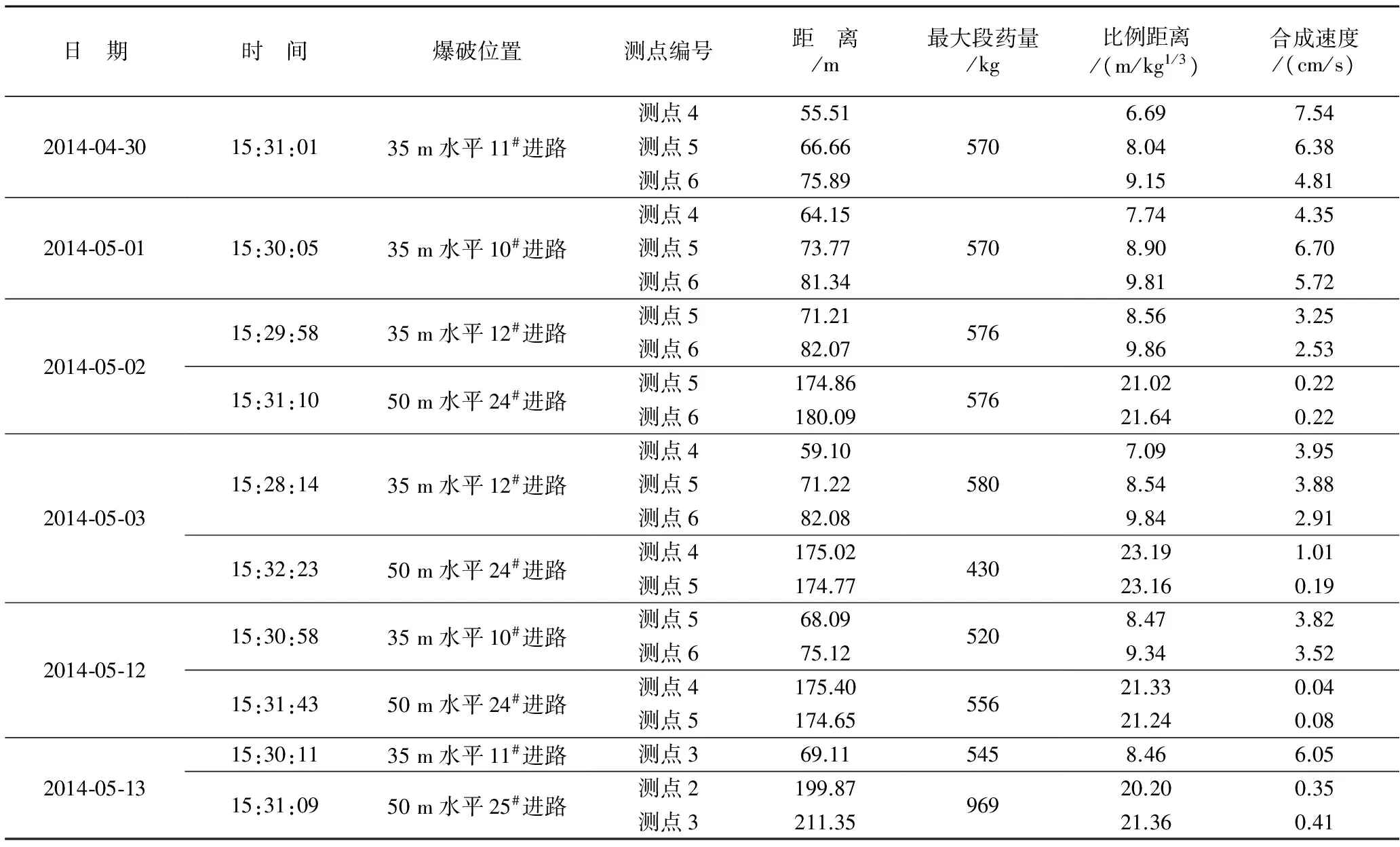
表5 爆破震动速度衰减模型计算参数

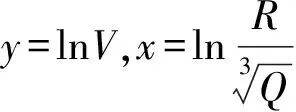
(3)

对于保国铁矿铁蛋山矿区来说，爆破所引起的下盘沿脉运输巷道破坏严重现象是亟需解决的问题。尽管控制爆破震动危害有多种方案，但是现阶段研究成果中显示，影响爆破震动的主要因素是最大段药量，随着最大段药量的增加，沿脉巷道的质点震动速度增加。因此，如何在生产爆破过程中控制最大段药量，就成为控制爆破震动危害的关键。为了保护铁蛋山矿区下盘沿脉运输巷道，根据爆破震动测试所获得

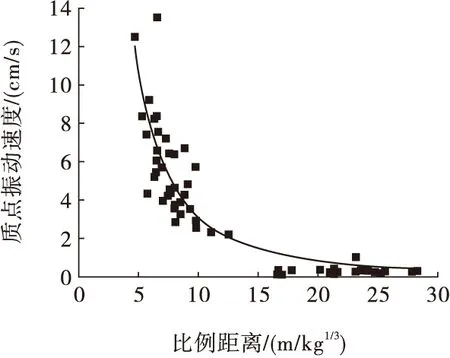
图5 振速随比例距离变化关系

的爆破振速衰减公式，结合《爆破安全规程》矿山巷道所允许的最大爆破震动速度要求，计算得到了铁蛋山矿区距离下盘沿脉运输巷道不同距离所对应的最大单段药量，如表6所示。

目前，铁蛋山矿最大单段药量在500～1 200 kg之间，以500～650 kg为主。从表6中可以看出，距离35 m时，允许的最大段药量为574.83 kg，与目前铁蛋山矿现阶段实际单排最大段药量相近。距离40 m时，允许的最大段药量为858.06 kg，距离50 m时，允许的最大段药量为1 675.89 kg。而小于35 m时，目前实际的最大单段药量要高于允许药量。

表6 各距离对应的允许最大段药量

对于铁蛋山矿区来说，主要开采分段+35 m水平矿体距下盘沿脉巷道最近距离4.23 m，最远232.57 m；+20 m水平矿体距下盘沿脉巷道最近距离11.62 m，最远231.29 m，矿体呈不规则脉状，沿脉运输巷道岩体破碎，支护良好。沿脉巷与矿体距离主要集中在15～150 m之间。结合表5所得结果，建议矿山在距离下盘沿脉运输巷道小于35 m时，采区增加分段数量或者减缓回采进度的方法，降低最大单段药量，控制爆破震动对于沿脉运输巷道造成损害。当距离下盘沿脉运输巷道35～50 m时，保持现有最大单段药量即可；当距离下盘沿脉运输巷道大于50 m时，可增加单段药量，加大回采进度，这样即保证了沿脉运输巷道的稳定性，也增加了产能效率。

4 结 论

(1)针对辽宁北票保国铁矿铁蛋山矿区爆破震动造成下盘沿脉运输巷道破坏严重的现状，开展了爆破震动测试工作，多点爆破情况下存在着信号与爆源识别困难的问题。对于完整爆破信号数据，采用最小比例距离Rm，min所对应的爆心距R、炸药量Q和最大振速值V可以有效解决该问题，为萨道夫斯基公式计算提供参数。经实例验证，此方法是可靠的。

(2)通过现场实测数据，建立了铁蛋山矿区爆破震动速度衰减模型，获得了距离下盘沿脉运输巷道不同位置开采时所允许的最大单段药量。

(3)对矿山回采过程中的爆破参数进行了改进，建议距离下盘沿脉运输巷道小于35m时，降低最大单段药量，控制爆破震动对于沿脉运输巷道造成损害；当距离下盘沿脉运输巷道35～50m时，保持现有最大单段药量；当距离下盘沿脉运输巷道大于50m时，增加单段药量，保证了沿脉运输巷道的稳定性和产能需求。

[1] 凌同华.爆破震动效应及其灾害的主动控制[D].长沙：中南大学，2004. Ling Tonghua.Blast Vibration Effect and Initiative Control of Vibrational Damage[D].Changsha:Central South University，2004.

[2] 臧秀平，汪 宏.爆破震动速度衰减方程形式初探[J].金属矿山，2002(4):36-37. Zang Xiuping，Wang Hong.Preliminary exploration of the velocity attenuation equation form of blast vibration[J].Metal Mine，2002(4):36-37.

[3] 陈钧潘.爆破震动公式中K值上下限的探讨[J].爆破,1996，13(2):12-15. Chen Junpan.Determination of lower and upper limits ofKin equation of blasting vibration[J].Blasting，1996，13(2):12-15.

[4] 吕 涛，石永强，黄 诚，等.非线性回归法求解爆破震动速度衰减公式参数[J].岩土力学，2007，28(9):1871-1878. Lu Tao，Shi Yongqiang，Huang Cheng，et al.Study on attenuation parameters of blasting vibration by nonlinear regression analysis [J].Rock and Soil Mechanics，2007，28(9):1871-1878.

[5] 张继春,彭琼芳.岩体爆破地震波衰减规律的现场试验与分析[J].辽宁工程技术大学学报:自然科学版，2001，20(4):399-401. Zhang Jichun，Peng Qiongfang.Field experiment and its analyses of attenuation law for seismic waves resulting from rock blasting [J].Journal of Liaoning Techinical University：Natural Science，2001，20(4):399-401.

[6] 李洪涛，舒大强.爆破震动衰减规律的影响因素[J].武汉大学学报:工学版，2005，38(1):79-82. Li Hongtao，Shu Daqiang.Influential factors analysis of blasting vibration attenuation law[J].Engineering Journal of Wuhan University，2005，38(1):79-82.

[7] 刘美山，吴从清，张正宇.小湾水电站高边坡爆破震动安全判据试验研究[J].长江科学院院报，2007，24(1):40-43. Liu Meishan，Wu Congqing，Zhang Zhengyu.Experimentation of judging standard of blasting vibration safty in high slope excavation of hydropower station[J].Journal of Yangtze River Scientific Research Institute，2007，24(1):40-43.

[8] 王民寿，郭庆海.用双随机变量回归改进爆破振速回归分析[J].爆炸与冲击，1998，18(3):283-288. Wang Minshou，Guo Qinghai.Regression analysis of blasting vibrational velocity by the double random variable method[J].Explosion and Shock Waves，1998，18(3):283-288.

[9] 宫风强，李夕兵.岩爆发生和烈度分级预测的距离判别方法及应用[J].岩石力学和工程学报，2007，26(5):1012-1018. Gong Fengqiang，Li Xibing.A distance discriminate analysis method for prediction of possibility and classification of rockburst and its application[J].Chinese of Rock Mechanics and Engineering Journal，2007，26(5):1012-1018.

[10] 张在晨，林从谋，黄志波，等.隧道爆破进去振动的预测方法[J].爆炸与冲击，2014，34(3):367-372. Zhang Zaichen，Lin Congmou，Huang Zhibo，et al.Prediction of blasting vibration of area near tunnel blasting source[J].Explosion and Shock Waves，2014，34(3):367-372.

[11] 逄焕东，陈士海.弹性介质中爆破地震波传播的分区变化规律研究[J].振动与冲击，2009，28(3):105-107. Pang Huandong，Chen Shihai.Variation law of blasting seismic wave’s propagation in elastic media[J].Journal of Vibration and Shock.2009，28(3):105-107.

(责任编辑 石海林)

Study on Velocity Attenuation Law for Multi-point Blasting Vibration

Liu Jianpo1Xu Hongliang2Wang Shaoquan2Cheng Chongqiang2Jing Hongdi1

(1.KeyLaboratoryofMinistryofEducationonSafeMiningofDeepMetalMines，NortheasternUniversity，Shenyang110819，China;2.NorthernEngineering&TechnologyCorporation，MCC，Dalian116600，China)

Blasting vibration is a key factor to induce the destruction of tunnel in underground mine.Therefore，it is important to obtain velocity attenuation law for blasting signals，and to reduce the damage from blasting vibration，which is meaningful to the safe and efficient production.In view of the footwall strike-drift seriously destructed by blasting vibration in Tiedanshan mine，the monitoring work for blasting vibration was carried out.For integrated blasting signals，the minimum scale distance was used to obtain the relationship between distances from center of explosion，explosive quantity and maximum vibration velocity.This method provided calculating parameter for Sadov's formula，whose reliability was verified.On this basis，the velocity attenuation model velocity attenuation model of blasting signals in Tiedanshan mine was established，and the largest amount of explosives per delay interval of different distance to footwall strike-drift were obtained.Then，the blasting parameters in Tiedanshan mine were improved.The measures that use the different largest amount of explosives per delay interval in different areas can meet the requirements of stability of footwall strike-drift and production capacity.

Blast vibration，Velocity attenuation，Multiple positions blasting，Sadov's formula，Safety control

2015-06-09

国家自然科学基金项目(编号：51204030)，“十二五”国家科技支撑计划项目(编号：2013BAB02B01,2013BAB02B03)，中国中冶“三五”重大科技专项(编号：0012012009)。

刘建坡(1982—)，男，讲师，博士。

TD853

A

1001-1250(2015)-10-024-05