基于反卷积干涉法的土层地震反应特性研究
王 飞 Kalkan Erol 任志林
1) 中国北京100081中国地震局地球物理研究所 2) 中国北京100080北京市地震局 3) 美国加利福尼亚州门洛帕克94025美国地质调查局地震科学中心
基于反卷积干涉法的土层地震反应特性研究

1) 中国北京100081中国地震局地球物理研究所 2) 中国北京100080北京市地震局 3) 美国加利福尼亚州门洛帕克94025美国地质调查局地震科学中心
美国阿拉斯加安克雷奇德兰尼公园的土层地震反应观测台阵建有6个井下观测点和1个地表观测点, 每个观测点设置一个三分量加速度传感器, 该台阵建成后记录了多次地震事件. 本文通过反卷积地震干涉法对这些地震记录进行土层反应分析, 根据该分析结果提取土层结构的等效剪切波速和阻尼比. 所有层位的地震记录对地表记录的反卷积波形均反映出在土层中传播的上、 下行波, 其上行与下行至每一层的时间差别明显. 根据每一层的到时差, 确定土层中的等效剪切波速和分层等效剪切波速, 该结果与现场土层等效剪切波速测试结果吻合较好; 根据等效剪切波速计算出的土层卓越频率, 其一致性亦较好; 根据上、 下行波的峰值分析确定该场地土层的等效阻尼比, 也与软土的阻尼比经验值相当. 这些参数为后续的土层反应模拟和土结相互作用研究奠定了良好的数据基础. 结果表明, 反卷积干涉法能够用于土层反应分析和土层地震反应特性的提取.
土层反应 波动传播 反卷积分析 等效剪切波速 卓越频率 阻尼比
引言
具有软土沉积层地区的地震灾害往往较为严重, 例如1964年美国阿拉斯加地震对安克雷奇城区造成的严重破坏和1989年旧金山湾区在洛马·普里埃塔地震中遭受的重大损失, 都是由于上述地区沉积层中存在较厚的液化土层造成的. 然而, 这种土层的放大特性尚未获得在破坏性地震动作用下的原位测试证据(Borcherdtetal, 2005). 而建设土层地震反应观测台阵的目的在于研究土层动力特性、 地震波传播、 土层放大效应和非线性效应(谢礼立, 于双久, 1982). 一旦土层地震反应观测台阵记录到强震动观测数据, 对研究土层地震反应和土层动力特性等工作意义重大. 本文根据美国阿拉斯加德兰尼公园土层地震反应观测台阵记录到的地震事件, 通过引入一维地震波传输模型(Halletal, 1995; Iwan, 1997), 对该台阵中不同层位的地震记录进行地震干涉分析, 从复杂的地震记录中提取土层反应和土层振动特性参数.
地震干涉分析法分为互相关干涉法和反卷积干涉法, 其中前者的相关研究实例较多(Shapiroetal, 2005), 这里不再赘述. 本文主要利用反卷积干涉法进行分析. 该方法可以在输入信号参数未知的情况下, 通过重建出同一信号不同接收点间的脉冲响应, 建立具有因果关联的物理波场. 人工设置的这种虚拟振动源产生的特殊波场与原波场系统波动方程相同, 只是边界条件不同. 研究表明边界条件的差异不会影响系统振动特性的识别. 该方法不仅可用于开展结构地震反应分析(Snieder,afak, 2006), 还可用于合成反卷积干涉波场来分析地震波在建筑结构中的传播效应 (Kohleretal, 2007). 此后该方法逐渐被广泛应用于提取结构地震响应的研究中, 我国地震工程研究者也开展了通过对地铁振动信号的反卷积干涉分析识别结构振动特性的相关研究(罗桂纯等, 2011). 目前该方法较多地应用在结构地震反应分析方面, 在土层反应分析和土层特性参数识别方面的应用较少, 其主要原因在于土体的分层明确, 且没有建筑物均匀的材料属性, 动力特性比建筑结构更加复杂. 当前, 如何应用反卷积干涉法开展土层地震反应研究逐渐引起地震工程研究者的注意(王飞等, 2014). 本研究有效地检验了反卷积干涉法在土层反应研究中的适用性.
1 台阵概述
美国阿拉斯加安克雷奇城区坐落在阿拉斯加俯冲带上, 该地区地震活跃, 历史上曾发生过多次具有严重破坏性的地震. 因此, 在该地区布设土层地震反应及结构地震反应观测台阵意义重大. 2003年美国国家地震台网在该地区的德兰尼公园建设了土层地震反应观测台阵. 该台阵由7个设置了三分量加速度传感器的观测点组成, 其中井下观测点6个, 地表观测点1个. 井下传感器1位于表层的冰水沉积层, 传感器2位于冰水沉积层下部的过渡层, 传感器3和4布设在本地区土层常见的河湾沉积层中, 传感器5和6位于最底层的冰碛层. 该观测台阵与间隔两个街区、 约500 m距离处的艾特伍德大楼的结构地震反应观测台阵相互关联. 艾特伍德大楼为20层钢筋混凝土结构, 布设有32个传感器. 该组合台阵的组成及位置关系如图1a所示. 土层地震反应观测台阵可为结构地震反应观测台阵提供精确的输入波场, 并为深入研究土结相互作用提供了原型振动试验依据(李鸿晶等, 2003).

图1 (a) 德兰尼公园土层地震反应观测台阵与附近的艾特伍德大楼结构地震反应观测台阵测点布设方案及位置关系示意图; (b) 土层地震反应观测台阵建设时现场原位波速测试结果
该场址的地层主要由晚更新世冰海和三角洲冰碛环境下沉积的淤泥质组成(Ulery, Updike, 1983). 其20—50 m深度范围的软土层被认为是沙土液化破坏的主要原因, 30 m附近土样的振动锤击数小于10次, 在该深度处的等效剪切波速逐渐减小(Steidl, 2006), 因此在该深度布设相应测点来记录该层位及其上下的地震动情况. 该台阵建设时进行了原位剪切波速测试和土动力学实验(Nathetal, 1997; Yangetal, 2008), 其等效剪切波速测试结果如图1b所示. 可以看出, 其平均值约为295 m/s, 不同层位土样的平均阻尼比约为2%. 图中井下传感器6埋置深度(61 m)处的等效剪切波速约为900 m/s, 认为此深度地层岩性为基岩.
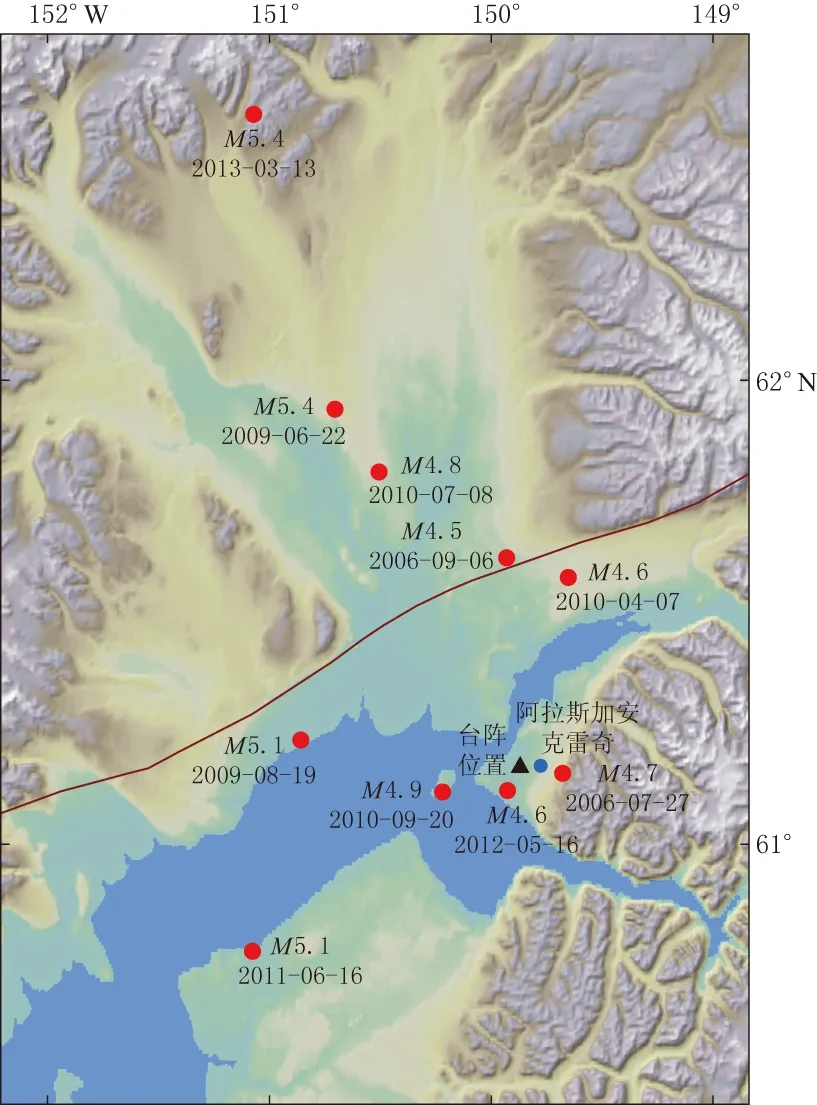
图2 本文所选择的10组地震位置
2 地震记录
德兰尼公园的土层地震反应观测台阵建成后, 记录了数十次地震事件, 本文选择震级为M4.5—5.4的10组地震事件进行分析. 所选择地震事件的参数详见表1, 各事件的震源位置及其与该台阵的分布关系见图2. 其中震中距最小的地震为2012年M4.6地震, 其峰值加速度为17.66 cm/s2.而峰值加速度最大的地震为2010年M4.9地震, 其峰值加速度为30.53 cm/s2. 之所以选择这些地震, 主要考虑在选定地震作用下该场址上的土层反应基本保持在线弹性状态. 由于信噪比太低, 本研究中并没有选择远震和小震. 选择10组地震进行研究, 能有效地减小某一地震事件对分析结果的决定性影响, 使得分析结果更为准确可信, 且该10组地震分布于台阵所处地震断层区的不同方向, 弱化了断层上下盘特性对地震记录的影响.

表1 本文所选择的10组地震事件参数
3 数据分析
本文的数据处理以表1中编号为1的地震事件(以下简称地震1)作为实例, 进行数据处理和分析过程展示. 地震1的加速度时程如图3所示. 可以看出, 峰值加速度的分布显示了土层结构的特点: 从井下传感器6到传感器3, 峰值加速度逐渐增加, 在软土层内部峰值也在不断增加; 位于软土层上部的传感器2记录到的峰值加速度明显减小, 甚至小于基岩处的峰值; 再往上传播, 峰值加速度又开始逐渐增加, 直至地表处达到最大. 单从峰值加速度分析表明该软土层发挥了一定的隔震作用.

图3 地震1的加速度时程及选定时间段
地震1的P波到时位于时程的第17 s, S波到时位于第19 s, 而最后到达的面波与场地土层发生共振作用, 共振振幅从下往上依次增加. 图3中设置了两个不同的时间段, 分别标记为时间段t1和t2. 其中时间段t1主要是P波和S波分量, 从P波到时开始持续时间约为10 s; 时间段t2是单一特性的面波分量, 从时程的30 s开始持续至60 s处. 分析时将时间段t1和t2分别添加零数填充至40 s时长.
3.1 反卷积波场
利用图3中设定的时间段t1中的加速度时程重建反卷积波场并识别土层振动特性. 将井下传感器1—6所获得的地震信号与地表传感器所记录的地震信号进行反卷积干涉分析, 其波形如图4a所示. 波形结果表明反卷积波场主要表现为上、 下行地震波动. 井下传感器1—6分别与地表传感器之间建立起一致的脉冲信号, 该信号在不同层位深度上表现为不同的行波到时. 脉冲信号首先到达井下传感器6, 随后逐渐波动上行, 依次到达其余各井下传感器, 最后传播至地表传感器; 然后地震波在地表发生反射, 反射后依次下行至井下传感器6. 这种简单的地震波传播特性较好地证明了地震波在土层某一卓越频率点上以一维波动模式传播, 表明一维波动模式适用于土层反应识别. 上、 下行波场中不同深度处的土层中并没有发生明显的分层内部反射, 表明土层固有的卓越频率大于不同深度处每个土层特定的反射系数. 已有研究认为连续介质的频率和质量决定了其对不同弹性波的反射系数(afak, 1999). 本土层中没有发生明显的分层内部反射过程, 表明地震波传播至该场地时频率相对较低. 若地震波波长较长, 则可能会达到多个土层的总厚度, 这样土层本身的反射作用会被压至更低. 对于高频成分, 如果土层的厚度大于地震波长, 此时分层土层中或许会有较弱的反射作用发生.

图4 (a) 图3中地震波形时间段t1的反卷积干涉波场; (b)时间段t1与t2的反卷积干涉波场对比
从图3中时间段t1数据得出的反卷积波场如图4a 所示. 利用时间段t2的数据同样计算出类似的反卷积波场, 两个不同时间段的数据分别构建的反卷积波场同时绘于图4b中. 对比发现两个反卷积波场具有较好的一致性. 这主要是因为时间段t1的主要成分是体波, S波频带较宽, 丰富的低频成分足以帮助构建出完整的脉冲信号; 而时间段t2中低频成分为主的面波往往掩盖了其中的高频成分, 反卷积干涉过程使两者表现出的高、 低频成分趋于一致. 对比分析结果表明, 土层的固有特性是决定基于反卷积波场识别出的土层反应信息的主要因素, 地震动时程中的不同频率成分对其影响较小. 虽然时间段t1与t2的持时不同, 但二者干涉分析结果却识别出非常接近的土层特性参数. 时间段t1的地震波分量的宽频带特性较好地稳定了其构建的反卷积波场, 使不同时间段的反卷积波形具有较好的一致性, 表明在该地震动作用下土层反应主要表现为线性, 土层的动力反应特性并未因该地震动输入而发生明显改变. 然而土层中也存在非线性反应的成分, 只是其不占主导作用, 反卷积波场的微小差别就印证了这一现象.
3.2 等效剪切波速
由于时间段t1与t2中数据计算出的反卷积波场较为一致, 故后续分析仅针对时间段t1中的数据进行. 图5a表示时间轴坐标选择[-0.3 0.3]段的反卷积波场, 这样更易辨识地震波在不同层位传感器间的传播轨迹和到时, 显示度较图4a明显提高. 利用地震波到达不同深度层位上的到时结合本场地土层厚度可计算出平均等效剪切波速. 假定上行波传播至不同深度的到时和该层位上加速度传感器的深度取负值, 而下行波的到时和相应深度取正值, 将这些到时和深度离散点绘制于时间-深度坐标系中, 对所有的离散点进行拟合, 确定最优拟合直线(图5b), 该直线的斜率即为该场地土层的等效剪切波速值. 根据上述方法, 利用地震1计算出的等效剪切波速为293 m/s.

图5 (a) 所有层位对地表传感器记录的反卷积波场; (b) 根据图(a)中的到时和各传感器的深度拟合出的最优化直线
同时, 根据走时差和分层厚度还可计算出上行波和下行波的等效剪切波速. 本文所选的10组地震的计算结果详见表2. 根据表中数据计算出的等效剪切波速与现场测试结果进行对比分析, 其结果示于图6.
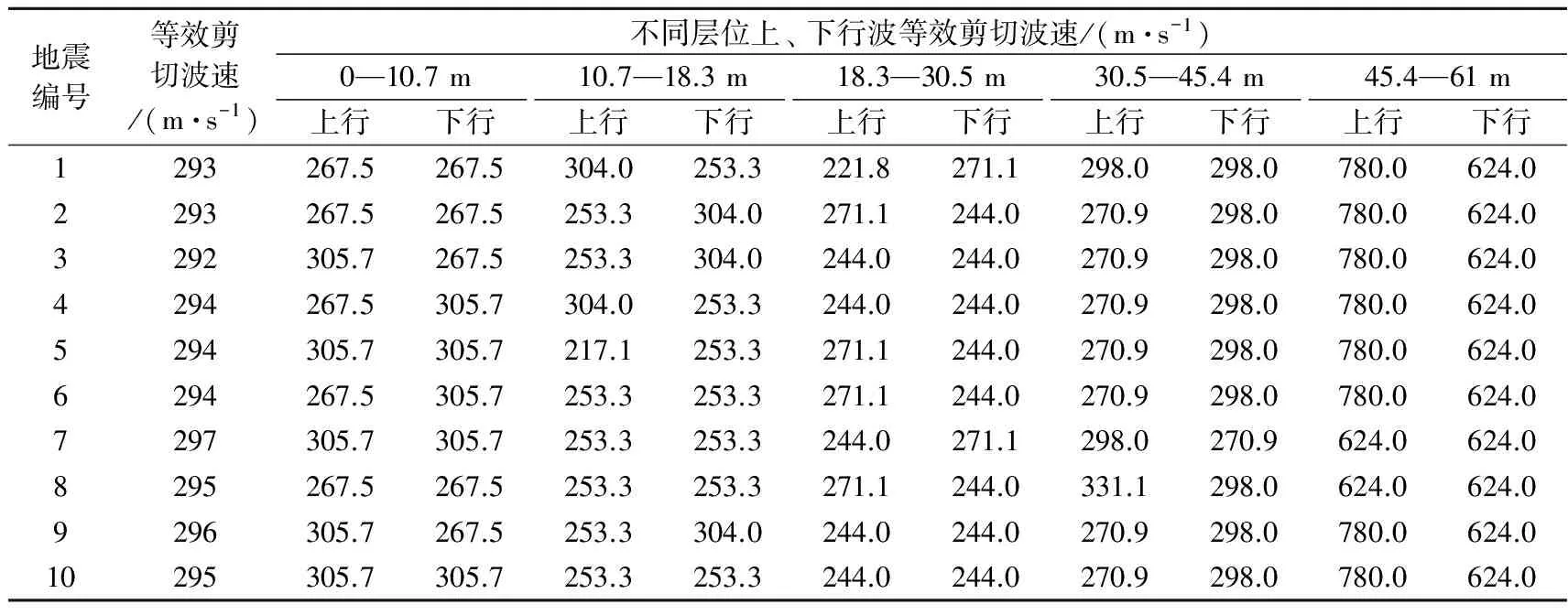
表2 该场址上和不同层位上的等效剪切波速Table 2 Equivalent shear wave velocities on the site and at different levels for the selected ten earthquakes

图6 现场原位测试(a)与上行(b)、 下行(c)波的分层等效剪切波速VS对比
3.3 卓越频率
土层的等效剪切波速和卓越频率是揭示土层动力反应特性的两个重要参数, 二者相互关联. 在本研究中引入的一维波动模型中, 如果将土层介质看成均匀介质, 该61 m土层的基振频率则可以根据前面的平均等效剪切波速计算得出, 其计算公式为
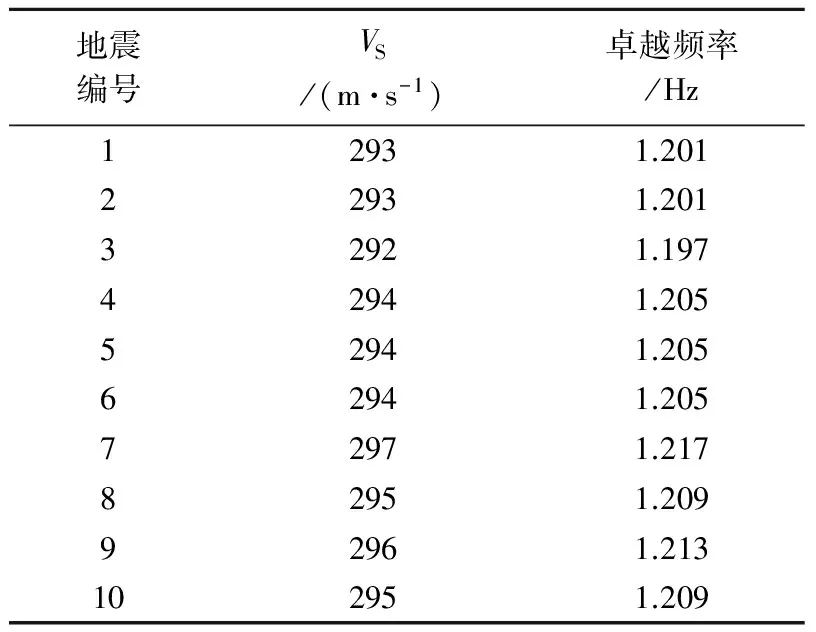
表3 由等效剪切波速计算出的土层卓越频率 Table 3 Soil predominant frequencies inferred from equivalent shear wave velocities
(1)
式中,f为土层基振频率,VS为土层等效剪切波速,H为井下传感器6的深度. 对于地震1而言, 其等效剪切波速为293 m/s, 据此得到在该地震作用下的土层基振频率为1.201 Hz. 照此方法将该10组地震作用下的土层基振频率全部计算出并列于表3, 其平均值为1.206 Hz. 尽管不同地震作用下的土层卓越频率略有差别, 但其最大差别约为2%, 满足工程精度要求.
3.4 阻尼
根据反卷积原理, 下行波与上行波比值的自然对数与其行进的距离存在线性关系, 拟合直线斜率与深度之间的关系式为
(2)
式中,k为拟合直线斜率,f表示反卷积波场的基振频率,γ代表阻尼比,VS为等效剪切波速.

图7 基于上、 下行波峰值比对数值与深度拟合的等效阻尼比曲线
计算图5中下行波峰值A下行与上行波峰值A上行的比值, 并将该比值的对数值与相应深度的两倍绘于图7. 可以看出, 点的离散度较大, 很难用于提取土层的等效阻尼比. 分析图7中的反卷积波场可知: 井下传感器1和2的上、 下行波之间存在明显的干涉效应, 该反卷积波峰不能作为判定土层衰减系数的依据; 井下传感器5和6的下行波峰值受到再次反射波的冲击, 使得其峰值偏大, 而井下传感器6的下行波受到的冲击更大, 峰值较上行波峰值大, 导致传感器5和6的数据无法使用. 因此本研究仅选择位于中间层位的井下传感器3和4 的反卷积波峰值来计算土层阻尼比. 基于二者对应的数值点拟合出的直线斜率k为-0.0052, 图7中反卷积波场的主频f约为14.7 Hz, 等效剪切波速VS为293 m/s. 据此计算出土层在地震1作用下的等效阻尼比约为1.65%. 用同样方法求出另外9组地震的等效阻尼比和平均阻尼比, 如表4所示. 10组地震等效阻尼比的离散度为5%, 该平均等效阻尼比值与软土土层等效阻尼比经验值接近.

表4 基于等效剪切波速的土层等效阻尼比Table 4 Soil equivalent damping ratios inferred from equivalent shear wave velocities
4 结论
本文将地震波在线弹性介质中的一维波动模型应用于反卷积地震干涉法, 研究美国阿拉斯加安克雷奇德兰尼公园建设的土层地震反应观测台阵处的土层等效剪切波速和阻尼比. 通过对该台阵记录的10组地震中的土层反应数据进行一维反卷积干涉分析, 重建出反卷积干涉波场, 识别出波场中的上行波和下行波. 对比分析发现, 不仅同一地震事件中的不同时间段计算出的反卷积干涉波场较为一致, 而且不同地震事件的反卷积干涉波场也基本类似且同样简单. 这说明人为构建的反卷积干涉波场和外在激发源与土层的反射特性等参数无关, 仅反映土层的振动特性和动力反应. 因此可以假定地震波在土层中进行一维传播, 通过计算土层的反卷积干涉波场来重建土层动力反应, 提取土层振动特性信息. 基于反卷积干涉波场能够确定地震波到达不同深度的时间, 根据该时间可计算出该土层的基振频率、 土层等效剪切波速及分层等效剪切波速分布, 分析发现其分布与原位波速测试结果基本一致. 根据等效剪切波速得出该场地上的土层卓越频率, 不同地震作用下的卓越频率差别不大. 同样可根据反卷积波场的峰值计算出土层的等效阻尼比, 其结果也与该场地土层的阻尼比经验值接近. 尽管文中所选10组地震的震级、 震中距和频率成分各不相同, 但其土层等效剪切波速及其分布与土层等效阻尼比等特性参数都基本一致. 本文结果表明, 基于一维波动模型的反卷积干涉法可用于开展土层地震反应分析和识别土层动力特性参数, 为基于波动的土层反应分析提供一种有效的方法.
北京市地震局胡平研究员对本文技术方法和数据结果的提取提出了宝贵意见, 美国地质调查局Ulusoy Hasan博士对本文计算程序的改进提供了很多帮助, 在此一并表示感谢.
李鸿晶, 朱士云, Celebi M. 2003. 强震观测建筑结构的地震反应分析[J]. 地震工程与工程振动, 23(6): 31--36.
Li H J, Zhu S Y, Celebi M. 2003. Seismic response analysis of an instrumented building structure[J].EarthquakeEngineeringandEngineeringVibration, 23(6): 31--36 (in Chinese).
罗桂纯, 刘澜波, 齐诚, 陈棋福, 陈永平. 2011. 基于地脉动和地铁振动的钢筋混凝土建筑结构响应分析[J]. 地球物理学报, 54(10): 2708--2715.
Luo G C, Liu L B, Qi C, Chen Q F, Chen Y P. 2011. Structural response analysis of a reinforced concrete building based on excitation of microtremors and passing subway trains[J].ChineseJournalofGeophysics, 54(10): 2708--2715 (in Chinese).
王飞, Erol K, Hasan U. 2014. 利用干涉法提取土层反应特性研究[C]∥中国地球科学联合学术年会. 北京: 中国和平音像电子出版社: 1251--1254.
Wang F, Erol K, Hasan U. 2014. Extracting the soil response characteristics using wave interferometry[C]∥AnnualMeetingofChinaGeoscienceUnion. Beijing: China Peace Audio Electronic Publishing House:1251--1254 (in Chinese).
谢礼立, 于双久. 1982. 强震观测与分析原理[M]. 北京: 地震出版社: 149--164.
Xie L L, Yu S J. 1982.TheoriesonStrongMotionObservationandAnalysis[M]. Beijing: Seismological Press: 149--164 (in Chinese).
Borcherdt R D, Glassmoyer G, Dietel C, Westerlund R E. 2005. Integrated surface and borehole strong-motion, soil-response arrays in San Francisco, California[J].NatoScienceSeriesIV:EarthandEnvironmentalSciences:DirectionsinStrongMotionInstrumentation, 58: 139--155.
Hall J F, Heaton T H, Halling M W, Wald D J. 1995. Near-source ground motion and its effects on flexible buildings[J].EarthqSpectra, 11(4): 569--605.
Iwan W D. 1997. Drift spectrum: Measure of demand for earthquake ground motions[J].JStructEng, 123(4): 367--404.
Kohler M D, Heaton T H, Bradford S C. 2007. Propagating waves in the steel, moment-frame Factor Building recorded during earthquakes[J].BullSeismolSocAm, 97(4): 1334--1345.
Nath S K, Chatterjee D, Biswas N N, Dravinski M, Cole D A, Papageorgiou A, Rodriguez J A, Poran C J. 1997. Correlation study of shear wave velocity in near surface geological formations in Anchorage, Alaska[J].EarthqSpectra, 13(1): 55--75.
Shapiro N M, Campillo M, Stehly L, Ritzwoller M H. 2005. High-resolution surface-wave tomography from ambient seismic noise[J].Science, 307(5715): 1615--1618.
Steidl J H. 2006. Inventory of existing strong-motion geotechnical arrays[C]∥InternationalWorkshopforSiteSelection,andOperationofGeotechnicalStrong-MotionArrays:Workshop2:GuidelinesforInstallation,Operation,andDataArchivingandDissemination. La Jolla, California: Cosmos Publication: 28--36.
Ulery C A, Updike R G. 1983.SubsurfaceStructureoftheCohesiveFaciesoftheBootleggerCoveFormation,SouthwestAnchorage,Alaska[R]. Alaska: Division of Geological and Geophysical Surveys: 1--5.
Yang Z H, Dutta U, Xiong F, Biswas N, Benz H. 2008. Seasonal frost effects on the dynamic behavior of a twenty-story office building[J].ColdRegSciTechnol, 51(1): 76--84.
Soil response characteristics to earthquakes based on deconvolution interferometry

1)InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China2)EarthquakeAdministrationofBeijingMunicipality,Beijing100080,China3)EarthquakeScienceCenter,U.S.GeologicalSurvey,MenloPark,California94025,USA
Seismic interferometry technique was used to extract the shear wave velocity and damping ratio of the soil at the Delaney Park, Anchorage Alaska from the measured soil response to ten earthquakes. The soil response is record-ed by a geotechnical array. This array consists of a surface and six borehole stations equipped with a tri-axial accelerometer each. Deconvolution of the waveforms recorded by the borehole accelerometers at various depths with the waveform recorded at the surface accelerometer manifests an upward and a downward travelling wave in the soil. The arrival times to each accelerometer are obvious so that the entire travel time and time differences are extracted from the deconvolved waveforms. The shear wave velocity and its profile estimated from the deconvolution analysis agree reasonably well with in-situ measurements. The predominant frequencies are also inferred from the shear wave velocity and they are basically consistent for the ten earthquakes. The damping ratio is similarly investigated from the amplitude attenuation of the upward and the downward travelling waves. The value of damping ratio coincides with the empirical damping ratio of the soft clay as well. Analysis indicates that wave deconvolution can be used to extract the soil response and its characteristics.
soil response; wave propagation; deconvolution analysis; equivalent shear wave velocity; predominant frequency; damping ratio
10.11939/jass.2015.03.009.
中国地震局青年科技骨干人才项目(201204190030)资助.
2014-06-27收到初稿, 2014-11-22决定采用修改稿.
e-mail: wangfei@bjseis.gov.cn
10.11939/jass.2015.03.009
P315.9
A
王飞, Kalkan Erol, 任志林. 2015. 基于反卷积干涉法的土层地震反应特性研究. 地震学报, 37(3): 463--472.
Wang F, Kalkan E, Ren Z L. 2015. Soil response characteristics to earthquakes based on deconvolution interferometry.ActaSeismologicaSinica, 37(3): 463--472. doi:10.11939/jass.2015.03.009.

