滨海斜坡复式护岸断面波浪爬坡试验研究

常 江，柳淑学＊，李金宣，代英男

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.中交第一航务工程勘察设计院有限公司，天津 300222）

0 引 言

护岸是保护海岸、河岸和湖岸使其免受水浪的冲击、侵蚀而构筑的水边设施［1］.现代护岸设计的内容要广泛得多，更强调景观性、亲水性和生态性.护岸与滨水的亲水设施一道成为内容涉及水利、土木工程、园林景观和艺术的综合性的水边环境设计［2］.护岸的形式多种多样，采用斜坡式结构是与较差地基和较浅水深等自然条件相适应的一种经济结构形式.复式断面护岸是常采用的一种斜坡式护岸结构，其前坡供游人进行亲水活动，后坡提供休闲娱乐的场所.从环境与景观的角度上看，在满足抵御波浪冲击、保障护岸安全的前提下，应尽量将护岸实体压低［3］.

当波浪相对较大时，波浪会沿着护岸斜坡上爬，在坡顶形成爬坡流.波浪爬高是滨海海堤堤顶高程确定的最重要因素［4］，同样也是堤式护岸堤顶高程确定的关键所在.此外，景观性护岸顶常有与休闲相关的建筑和设施，堤顶爬坡流的厚度往往是这些休闲设施设计的依据之一.波浪爬高的影响因素主要有波浪特性、斜坡坡度、斜坡护面结构形式和斜坡渗透等多种.目前，针对斜坡断面的波浪爬高，国内外许多学者进行了大量的研究，提出了多种经验计算方法.其中应用最广的有我国堤防设计规范中的方法［5］和欧美广泛应用的van der Meer法［6－8］.这些方法主要针对海堤前斜坡，且复式断面的前坡和后坡坡度相对较大，普遍大于1∶5，计算的结果为累计率为X%的爬高.而对于滨海护岸，堤顶后方一般为人活动区域，坡度较缓，大多取为3%左右，波浪爬坡流能够爬到的最大高度或者最大距离对于护岸的设计具有重要的影响.此外，最大爬坡高度和爬坡流厚度与护岸前沿处的越浪量具有直接关系，可以用护岸前沿的越浪量大小来反映.

针对目前工程设计需要，本文基于物理模型试验，研究不同堤顶高程在不同波浪要素作用下波浪沿滨海护岸断面爬坡范围和爬坡流不同位置处的厚度，探讨最大爬坡距离和爬坡流厚度的影响因素和其影响规律，建立爬坡距离和爬坡流厚度与护岸前沿越浪量的关系，在此基础上参考相关研究成果讨论比尺效应对试验结果的影响，以期为工程实际设计和相应数值计算模型的验证提供参考.

1 试验概述

越浪量的大小直接决定了滨海护岸顶岸边波浪的爬坡距离和大小，而护岸越浪量的研究相对比较成熟，因此本研究旨在建立波浪在滨海护岸顶岸边的爬坡距离和爬坡流厚度与护岸前沿越浪量的关系.试验针对光面斜坡护岸，在大连理工大学海岸和近海工程国家重点实验室的海洋环境水槽中进行，水槽长50m，宽3m，高1m，可同时产生波浪和水流.水槽的工作段在纵向分割成0.8 m 和2.2 m 两个部分，试验段设在0.8 m 宽 部分.水槽一端装有由微机控制的液压伺服造波机，由计算机自动控制产生所要求模拟的波浪.该造波系统可根据需要产生规则波和不同谱型的不规则波.水槽末端设有消浪斜坡和消波装置.试验水槽布置示意图如图1所示.

测量波浪爬坡高度和爬坡流厚度的试验布置如图2所示，堤前水深为0.4m，护岸坡度为1∶2，景观护岸工程护岸顶岸边区域考虑排水因素一般设有一定的坡度，但是考虑景观因素，坡度一般较缓，参考相关实际工程应用，本文试验研究的岸边坡度选较为常见的3∶100，试验模型中的堤顶超高Rc从小到大分别取0.06、0.08、0.10 和0.12m.测量水流厚度采用北京水利科学研究院研制的DJ800多点浪高仪采集处理系统，该系统可同步测量多点水面过程并进行数据分析，误差小于0.15%，波高分辨精度为±1mm.从堤顶开始，沿护岸每隔50cm 在斜坡上设置一个小水坑，里面灌满与斜坡平齐的水，深度约5cm，在里面设置浪高仪，当有水流流过测量点时，浪高仪上水面高度发生变化.本试验中一共设置了11个浪高仪，最大测量范围为距护岸前沿5.0m.

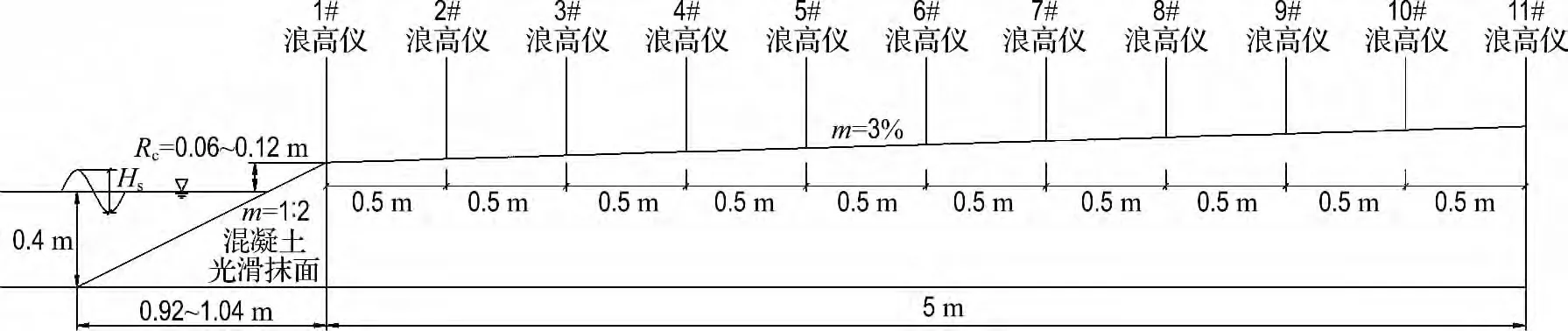
图2 波浪爬坡试验布置图Fig.2 Sketch of the experimental setup for the wave running upon slope revetment

表1 不规则波试验参数Tab.1 Irregular wave test parameters

试验采用不规则波，选取在当前水深下较大波高的不同波浪，但未破碎，不规则波波浪要素如表1所示.波浪频谱采用Goda 改进的JONSWAP谱［9］，时间间隔为0.02s，数据采集长度8 192，周期较长（1.8、2.0 和2.2s）时为16 384，波数为120～180个，每组试验重复3次.

2 试验结果分析

2.1 平均越浪量分析

为了研究波浪爬坡高度和爬坡流厚度与护岸前沿平均越浪量的关系，在建立斜坡模型前针对护岸前沿的平均越浪量进行了测量，测试方法和结果可参考代英男等［10］在相关试验研究中给出的结果.为了验证试验所得越浪量结果，将试验测得量纲一化平均越浪量与《海港水文规范》（JTJ 213—98）、欧洲国家推荐使用的van der Meer（VDM）方法，以及陈国平等给出的方法［11］的计算结果进行比较，结果如图3所示，图中给出了量纲一化平均越浪量与相对堤顶超高Rc／Hs的关系.从图中可以看出，试验值在规范方法与VDM 方法和陈国平方法之间，略大于规范方法计算结果，变化趋势与规范方法和陈国平等方法［11］一致.因此可以根据实际需要采用规范方法或陈国平方法［11］来计算护岸前沿的越浪量.

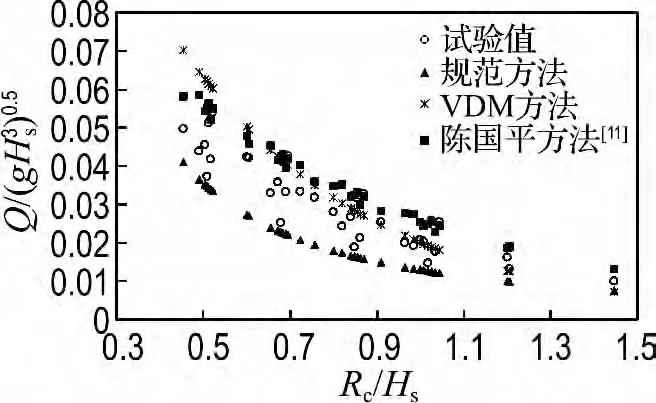
图3 波浪平均越浪量试验结果与规范方法、VDM 方法和陈国平方法比较Fig.3 Comparison between experimental results and calculated results by Standard，VDM and Chen Guo－ping methods

2.2 波浪爬坡试验数据处理

最大爬坡高度是指一组波浪作用下，波浪爬上护岸后能够爬到的相对护岸前沿的最大高度或者距离，体现了波浪在护岸上的爬坡能力，也反映了斜坡护岸上的最大浸水范围.为了直观体现这种爬坡能力，试验中采用沿护岸能够爬到的最大距离，用Lmax来表示.在斜坡上目测波浪能够爬到的最远位置，测量此位置距斜坡前沿的距离即为波浪沿斜坡的最大爬坡距离.

在不规则波作用下，浪高仪测得的水面高度典型过程线如图4所示.可以明显看出，不规则波作用下，爬坡流水面高度也呈现出不规则的变化.如前所述，每个浪高仪放置在斜坡上的小水坑中，里面灌满与斜坡平齐的水，因此每组试验中，基准零点为试验过程中采集到的水面高度最小值，通过计算采集到的水面高度与该基准零点的差得到爬坡流厚度.为了得到稳定的试验结果，取前1／3个厚度峰值的平均值为研究对象，用hc来表示.此外，在实际工程应用中，最大厚度往往也很重要，所以也研究了每组试验的最大厚度峰值，用hcmax来表示.为了分析波浪沿护岸最大爬坡距离、爬坡流厚度和各影响因素之间关系，需要将物理量进行量纲一化处理.考虑各物理因素的影响，本文相对最大爬坡距离定义为L＊max＝Lmax／Hs，爬坡流厚度定义为h＊c＝hc／Hs，量纲一化越浪量Q＊＝距护岸前沿相对距离L＊a＝La／Hs，其中La为浪高仪距护岸前沿的距离，Hs为有效波高.

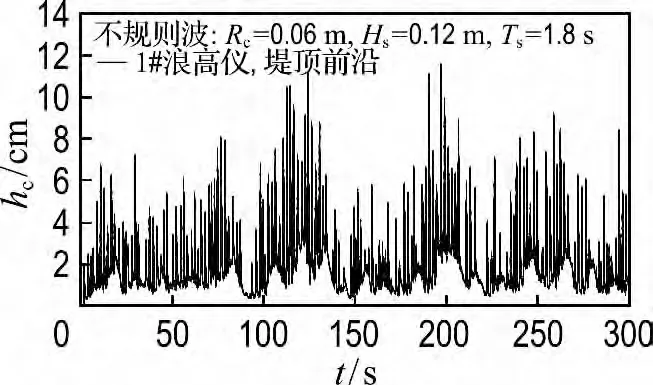
图4 不规则波作用下护岸上波浪爬坡流的水面过程线Fig.4 The surface course of wave run－up flow on revetment with irregular wave

2.3 最大爬坡距离与护岸前沿平均越浪量关系

图5给出了试验所得波浪沿护岸相对最大爬坡距离Lmax／Hs与量纲一化越浪量的关系.从图中可以看出随着量纲一化越浪量的增大，相对最大爬坡距离也增大，考虑当越浪量为0时的爬坡距离为0，因此采用幂指数关系拟合后得到的最大爬坡距离Lmax／Hs与量纲一化越浪量的关系为

图6为式（1）的计算结果（Lmax／Hs）c和试验结果（Lmax／Hs）e的比较，可以看出计算结果和试验结果符合良好.

2.4 爬坡流厚度与护岸前沿平均越浪量关系

爬坡流厚度取决于护岸前沿平均越浪量和距护岸前沿的距离，因此需要考虑在距护岸前沿相对距离相同的情况下，爬坡流厚度与护岸前沿平均越浪量的关系.图7给出了不同位置试验测得的爬坡流厚度与量纲一化越浪量的关系，可以看出，各组次中相对爬坡流厚度随着平均越浪量的增大而明显增大.

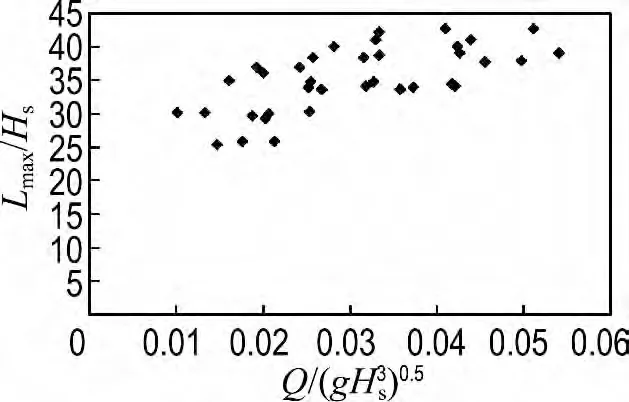
图5 波浪沿护岸相对最大爬坡距离与护岸前沿量纲一化平均越浪量的关系Fig.5 The relationship between relative maximum wave ascent and the dimensionless average wave overtopping discharge at the front of slope

图6 波浪沿护岸最大爬坡距离试验值和计算值的比较Fig.6 Comparison between experimental value and calculated value of maximum wave ascent at the front of slope

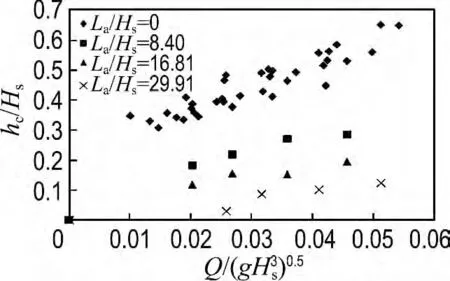
图7 相对爬坡流厚度与护岸前沿量纲一化平均越浪量的关系Fig.7 The relationship between relative thickness of wave run－up flow and the dimensionless average wave overtopping discharge at the front of slope

2.5 爬坡流厚度与距护岸前沿距离关系

图8为相同量纲一化越浪量情况下，相对爬坡流厚度hc／Hs与相对距护岸前沿距离La／Hs的关系，可以看出，相对爬坡流厚度随着相对距护岸前沿距离的增大而明显减小，并且各试验结果减小的趋势大致相同.

图8 相对爬坡流厚度与相对距护岸前沿距离的关系Fig.8 The relationship between relative thickness of wave run－up flow and the relative distance from slope front

2.6 爬坡流厚度计算经验公式

为了得到不同位置处爬坡流厚度计算的经验公式，首先建立护岸前沿处的爬坡流厚度计算公式，在此基础上，进一步建立爬坡流厚度沿斜坡衰减系数的公式，因此不同位置处的相对爬坡流厚度可以写为

式中：hc0／Hs为护岸前沿处的相对爬坡流厚度；Cr为爬坡流厚度沿斜坡的衰减系数，定义为距护岸前沿一定距离处的爬坡流厚度与护岸前沿爬坡流厚度的比，显而易见，衰减系数Cr受相对距护岸前沿距离La／Hs的影响.

类似于波浪沿斜坡最大爬坡距离的分析，参考图5，当越浪量为0时，护岸前沿的爬坡流厚度亦为0，可采用幂指数关系来拟合护岸前沿处爬坡流厚度与护岸前沿平均越浪量的关系，得到如下计算公式：

为了得到爬坡流厚度的衰减系数，图9给出了试验分析所得Cr随La／Hs的变化情况.可以看出，随着La／Hs增大，Cr明显减小.采用指数关系进行拟合可得到如下关系式：

把式（3）和（4）代入式（2），则可以得到波浪沿护岸相对爬坡流厚度hc／Hs与相对距护岸前沿距离La／Hs和护岸前沿量纲一化平均越浪量Q／的关系：

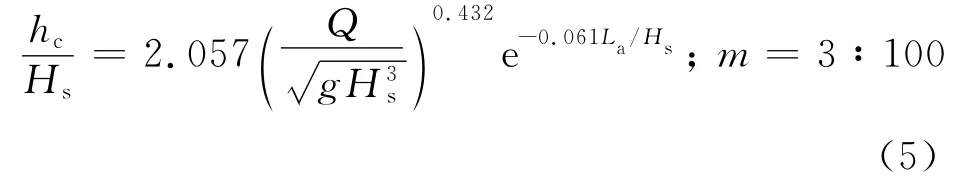
式（5）的计算值和试验值的比较如图10 所示，从图中可以看出，计算值与试验值符合良好.需要说明的是，式（5）中La／Hs的最大取值为由式（1）计算所得的值.

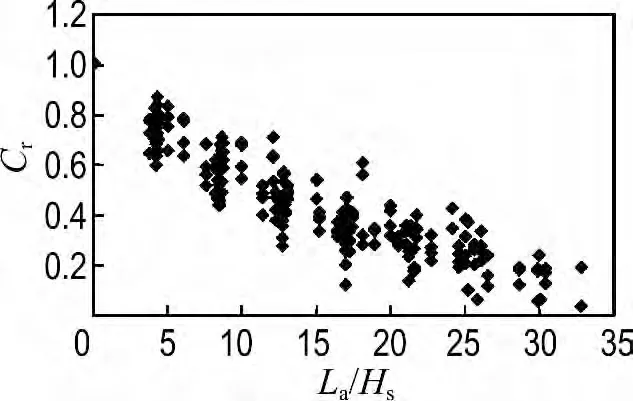
图9 衰减系数Cr 与相对距护岸前沿距离La／Hs 的关系Fig.9 The reduction degree of flow thickness Cr with the relative distance from slope front La／Hs

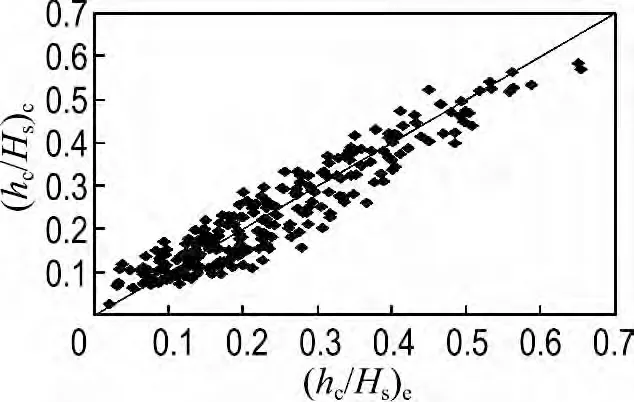
图10 波浪爬坡流厚度计算值与试验值的比较Fig.10 The comparison between experimental value and calculated value of thickness of wave run－up flow

2.7 爬坡流最大厚度分析

以上给出的是不规则波作用下爬坡流厚度的有效值（1／3值），为了得到爬坡流的最大值，图11给出了爬坡流厚度统计的1／3 值（hc）和最大值（hcmax）的关系，可以看出，两者近似符合线性关系，最大值约为1／3值的1.626倍，即

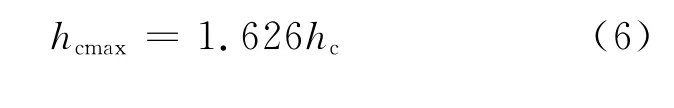
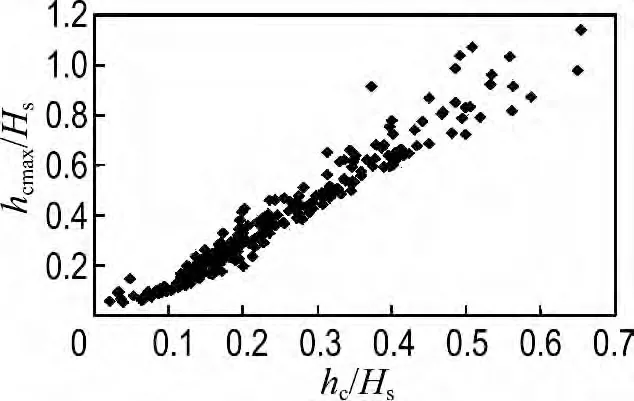
图11 波浪爬坡流厚度最大值与1／3值的关系Fig.11 The relationship between maximum and 1／3 thickness of wave run－up flow

3 比尺效应的影响分析讨论

本文基于模型试验建立了爬坡流距离和厚度与越浪量之间的关系，由于比尺效应的问题，其对于原型实际工程的适用性需要进一步研究.事实上，由于原型观测的复杂性，目前相关的研究成果大多是在物理模型试验研究的基础上给出的，而试验的比尺效应对于波浪越浪、爬高、护面块体稳定等的影响一直是人们关心的问题.

在越浪量研究方面，van der Meer等［12］通过1∶7和1∶35两个比尺的模型试验研究，得出两个比尺下堤前波浪反射情况和越过堤顶波浪个数接近，即越浪量接近，无实质区别.李晓亮［13］在越浪量研究中提到De Rouck等［14］总结的一些海防建筑物原型实测越浪量，将这些结果与一些试验结果进行对比，认为光滑斜坡堤的比尺效应可以忽略.欧洲《海防建筑物越浪手册》［15］中也提到，对于光滑斜坡堤，比尺效应调整系数为1.0，即可以不考虑比尺效应的影响.而在波浪爬高方面，欧洲《海防建筑物越浪手册》［15］中，总结了不同比尺下的波浪在斜坡上的爬高试验数据，并将其与经验公式进行对比，认为在不同比尺下波浪爬坡的变化规律相同.杨运泽［16］通过模型试验研究得出，用小比尺模型试验，实际爬坡高度会估计得偏小，而Ahrens［17］采用不规则波在光滑斜坡上的爬坡研究中提到Stoa等［18－19］通过比尺为1∶20和1∶40的模型试验研究，得出爬坡比尺效应调整系数随结构物坡度的变化.总体来讲，在模型比尺1∶20和1∶40条件下，比尺效应的影响取决于结构物的坡度，1∶1.5坡度时最大影响系数为14%，坡度越陡或越缓，比尺效应的影响越小，当坡度小于1∶8时，比尺效应的影响在5%以内.

本文模型试验的模型设计是在参考相关工程的基础上进行的，模型试验的比尺在1∶20～1∶30，因此在应用本文试验成果时，可以根据实际工程情况，适当考虑比尺效应的影响.

4 结 论

（1）波浪在护岸上后方的最大爬坡距离随着护岸前沿平均越浪量的增大而增大，并且建立了最大爬坡距离与量纲一化越浪量的关系.

（2）护岸顶爬坡流的厚度与护岸前沿平均越浪量和距护岸前沿距离有关，随着越浪量的增大，爬坡流厚度增大，随着距护岸前沿距离的增大，爬坡流厚度减小.

（3）在护岸顶岸边坡度为3∶100情况下，分别建立了护岸前沿处相对爬坡流厚度与量纲一化平均越浪量的关系以及爬坡流厚度沿斜坡的衰减系数与相对距护岸前沿距离的关系，在此基础上，建立了爬坡流厚度与护岸前沿平均越浪量和距护岸前沿距离的关系.

（4）分析了在一定越浪量条件下，爬坡流厚度的最大值和1／3 值的关系，总体来讲，最大值是1／3值的1.626倍.

（5）基于现有的参考资料和研究成果，分析了比尺效应对于越浪和波浪爬坡等的影响规律，综合各方面研究成果，对于光滑斜坡，越浪量受比尺效应的影响可以忽略，但比尺效应对于波浪的爬坡具有一定的影响，其影响取决于结构的坡度，坡度在1∶1.5时最大在14%左右，当坡度小于1∶8时，比尺效应的影响在5%以内.

本文参考相应实际工程进行了护岸顶岸边坡度为3∶100的模型试验，研究成果可以为相应数值模型提供验证依据，同时也可以为相关工程设计提供基本的参考.总体来讲，在护岸前沿越浪量一定的情况下，坡度越缓，爬坡距离越大，沿程厚度越小.不同坡度堤坝情况下的爬坡流厚度和距离还应进一步研究.

［1］ 河川治理中心.滨水地区亲水设施规划设计［M］.北京：中国建筑工业出版社，2005.Center for River Governance.Water Affinity Facilities Planning and Design of Waterfront［M］.Beijing：China Building Press，2005.

［2］ 张丙印，倪广恒.城市水环境工程［M］.北京：清华大学出版社，2005.ZHANG Bing－yin，NI Guang－heng.City Water Environment Engineering ［M］.Beijing：Tsinghua University Press，2005.

［3］ 何元瑭，陆明生.新型景观护岸结构设计［J］.水运工程，2005（4）：39－41.HE Yuan－tang，LU Ming－sheng.A new－type landscape revetment structural design［J］.Port ＆Waterway Engineering，2005 （4）：39－41.（in Chinese）

［4］ 苗 青，江 洧.波浪在海堤上的爬高及消浪措施研究综述［J］.广东水利水电，2007（6）：5－7，22.MIAO Qing，JIANG Wei.The review of studies of wave run－up on seawall and wave dissipation measures ［J］.Guangdong Water Resources and Hydropower，2007（6）：5－7，22.（in Chinese）

［5］ 水利部水利水电规划设计总院.GB 50286—98 堤防工程设计规范 ［S］.北京：中国计划出版社，1998.China Renewable Energy Engineering Institute.GB 50286－98Code for Design of Levee Project［S］.Beijing：China Planning Press，1998.（in Chinese）

［6］ U.S.Army Corps of Engineers.Coastal Engineering Manual，Engineer Manual 1110－2－1110［M］.Washington D C：U.S.Army Corps of Engineers，2004.

［7］ Krystian W P.Dikes and Revetments Design：Maintenance and Safety Assessment ［M ］.Rotterdam：A.A.Balkema，1998：43－52.

［8］ Krystian W P.Geosynthetics and Geosystems in Hydraulic and Coastal Engineering［M］.Rotterdam：A.A.Balkema，2000：25－26.

［9］ Goda Y.A comparative review on the functional forms of directional wave spectrum ［J］.Coastal Engineering Journal，1999，41（1）：1－20.

［10］ 代英男，柳淑学，常 江，等.斜坡堤越浪流厚度及堤后次生波的试验研究［J］.水运工程，2011（12）：1－5.DAI Ying－nan，LIU Shu－xue，CHANG Jiang，et al.Experimental research on layer thickness of wave overtopping flow and secondary wave conditions over sloping breakwater ［J］.Port ＆Waterway Engineering，2011（12）：1－5.（in Chinese）

［11］ 陈国平，周益人，严士常.不规则波作用下海堤越浪量试验研究［J］.水运工程，2010（3）：1－6.CHEN Guo－ping，ZHOU Yi－ren，YAN Shi－chang.Test study on wave overtopping under irregular wave action ［J］.Port ＆ Waterway Engineering，2010（3）：1－6.（in Chinese）

［12］ van der Meer J W，Veldman J J.Singular points at berm breakwaters：scale effects，rear，round head and longshore transport［J］.Coastal Engineering，1992，17（3－4）：153－171.

［13］ 李晓亮.斜向和多向不规则波在斜坡堤上越浪量的研究［D］.大连：大连理工大学，2008.LI Xiao－liang.The study of overtopping on sloping seawall under oblique and multidirectional irregular waves ［D］.Dalian： Dalian University of Technology，2008.（in Chinese）

［14］ De Rouck J，Verhaeghe H，Geeraerts J.Crest level assessment of coastal structures — General overview ［J］.Coastal Engineering，2009，56：99－107.

［15］ Pullen T，Allsop N W H，Bruce T，etal.EurOtop：Wave Overtopping of Sea Defences and Related Structures －Assessment Manual ［M］.Hamburg：Kommissionsverlag，2007.

［16］ 杨运泽.模型比尺对块体稳定性及斜坡堤水力特性的影响［J］.港口工程，1995（1）：17－24.YANG Yun－ze.The model scale effects on the stability of armor blocks and hydraulic characteristics of breakwater［J］.Port Engineering，1995（1）：17－24.（in Chinese）

［17］ Ahrens J P.Irregular Wave Run－up on Smooth Slopes ［M］.Fort Belvoir：National Technical Information Services，Operations Division，1981.

［18］ Stoa P N.Reanalysis of Wave Run－up on Structures and Beaches［M］.Fort Belvoir：National Technical Information Services，Operations Division，1978.

［19］ Stoa P N.Revised Wave Run－up Curves for Smooth Slopes ［M］.Fort Belvoir：National Technical Information Services，Operations Division，1978.