基于IPSO-SVM的地铁车辆牵引控制单元故障诊断
徐晓璐,吴 涛,2,顾 宏*
(1.大连理工大学 控制科学与工程学院,辽宁 大连 116024;2.北车大连电力牵引研发中心有限公司,辽宁 大连 116045)
0 引 言
地铁是人员密集的公共交通系统,设施的自动化程度高,为保证地铁车辆安全稳定运行,高效、快速排查地铁车辆出现的故障并根据故障诊断结果给出相应的维修建议十分重要.牵引控制单元(TCU)是地铁车辆控制的重要组成部分,列车通过向牵引控制单元传输指令信息,实现对整车牵引系统的控制.因此必须始终保持牵引控制单元安全平稳的工作状态.
近几年随着人工智能诊断方法[1-4]的不断发展,神经网络被广泛用于地铁车辆的故障诊断.但神经网络存在过拟合、收敛速度慢、易陷入局部最优的缺点.而支持向量机(SVM)模型结构简单,克服了维数灾难和易陷入局部最优的缺点,且对小样本和非线性问题有很好的分类效果和泛化能力[5-6],已经得到了广泛关注,并逐渐应用于故障诊断中.由于地铁牵引控制单元故障诊断的复杂性和小样本特性,SVM 方法更适用于地铁的故障诊断.但在实际应用中SVM 方法还存在怎样选取参数能使其诊断性能达到最优的问题.众学者已经提出了一些解决办法,例如遗传算法、粒子群算法[6]等.但是这些方法涉及太多人为因素,并且优化过程中容易陷入局部最优.
为了克服这些缺点,本文采用改进粒子群优化(IPSO)算法优化SVM 参数的方法.改进粒子群优化算法利用混沌运动的规律性、遍历性、内部随机性来搜索最优参数,并且在优化过程中加入了识别过早停滞的方法,一旦发生了过早停滞,就重置个体最优位置和全局最优位置.最后通过实验验证这种方法的可行性.
1 SVM 分类器
SVM 是一种基于结构风险最小化原则的机器学习算法,最早应用于模式识别[7].设计一个非线性SVM 模型的基本思想是:通过预先选好的非线性映射函数把输入向量x∈Rn映射到高维特征空间F中,在此高维特征空间F中创建最优分类超平面.
最优分类超平面的决策函数如下:
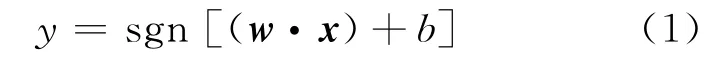
式中:sgn(·)是符号函数,w是权重向量,x是输入向量,b是常数.通过非线性映射函数φ(x)将数据映射到高维特征空间后,分类决策函数为
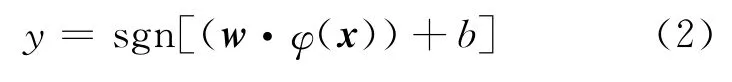
约束条件为
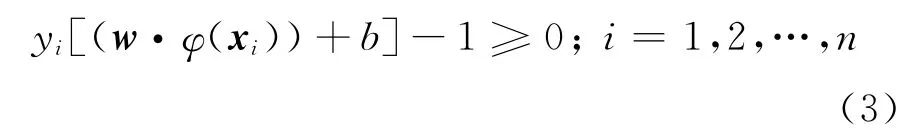
xi是指第i个训练数据,yi=±1.
根据VC维理论,在上述约束条件下使结构风险最小化,数学过程可表达为如下的二次规划问题:
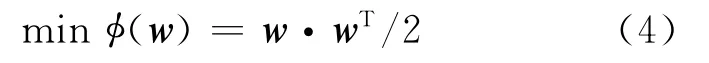
引入松弛变量ξi≥0.若样本被准确分类,那么ξi=0,否则ξi>0.则式(3)变为
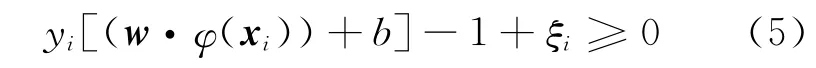
分类超平面应使两类样本距超平面的最小距离最大化,则优化的目标函数如下:
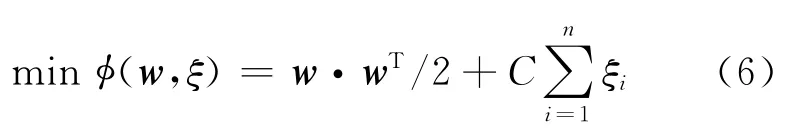
在式(6)中,惩罚因子C表示对错分样本的惩罚度.最小化过程中采用拉格朗日乘子和二次规划优化方法,转换后的对偶问题为
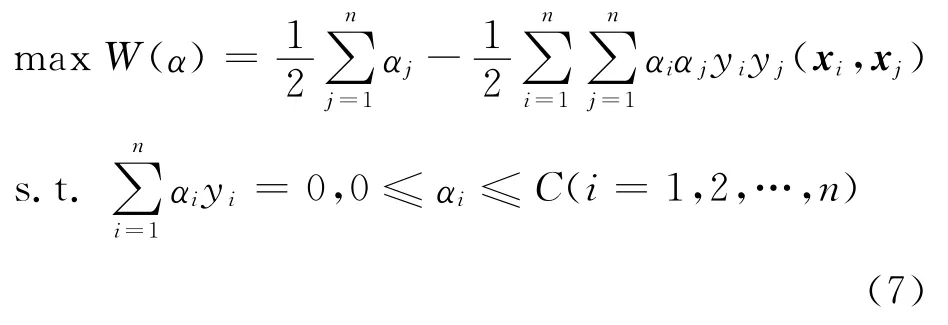
其中αi是拉格朗日乘子.则最优决策函数可表示为
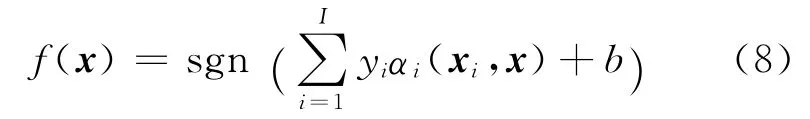
式中:I是支持向量的个数.对非线性问题,需要通过非线性映射把数据映射到更高维的特征空间.假设核函数K(xi,x)为非线性映射函数,则决策函数为
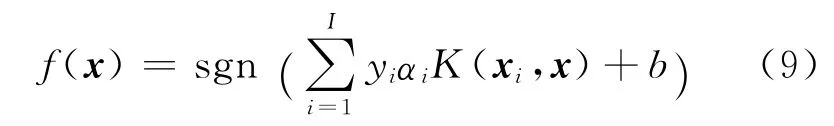
由于径向基核函数(RBF)只需确定一个参数,有利于参数优化,因此本文选择RBF 为核函数:
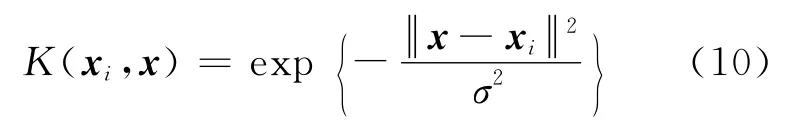
式中:σ是核函数宽度.
研究表明C和核函数参数是影响SVM 性能的主要因素[8-10].因此为了获得SVM 更好的泛化能力,要选择合适的C和核函数参数.本文用改进粒子群优化算法来优化C和核函数参数.
2 改进粒子群优化(IPSO)算法
2.1 标准粒子群优化算法
粒子群优化算法是一种由鸟群觅食演化而来的全局搜索算法,它通过分享群体间的历史信息和社会信息来搜索最优值.由于它的概念简单、收敛速度快,已经成功应用于许多领域[11-12].其基本思想是:每一个粒子在D维搜索空间中以一定的速度飞行,以适应值函数、粒子个体飞行经验和其他粒子飞行经验动态地调整粒子本身速度和最优位置,得到优化问题的最优解.
假设在D维搜索空间中由m个粒子组成一个群体,xi=(xi1,xi2,…,xiD)指第i个粒子的位置,vi=(vi1,vi2,…,viD)指第i个粒子的速度.第i个粒子的最优位置为pi=(pi1,pi2,…,piD),整个群体的最优位置为pg=(pg1,pg2,…,pgD).群体中粒子的速度和位置可以表示成如下方程:
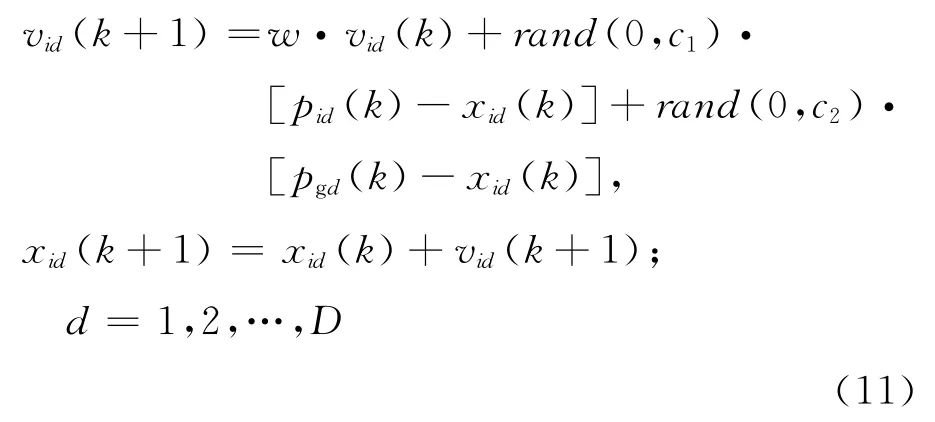
式中:c1、c2是加速常数,分别代表了一个粒子向局部最优位置(pid)和全局最优位置(pgd)飞行的加速权重;rand(0,c1)、rand(0,c2)分别是在[0,c1]、[0,c2]中均匀分布的随机数;w是惯性权重.
文献[11]中标准粒子群优化(PSO)算法的性能很大程度上依赖于粒子的数目和初始参数.且由式(11)知,当前个体位置是由pid和pgd共同决定的.如果pid和pgd都陷入局部最优,那么粒子将重复相同的搜索路径,称作过早停滞.本文提出能增强搜索多样性并克服过早停滞的改进粒子群优化(IPSO)算法来解决这一问题.
2.2 惯性权重的设定
w代表粒子前一次迭代速度对当前迭代速度的影响.w越大,粒子整体速度越大,粒子的搜索空间越大,有助于群体寻找新的解空间,即种群全局搜索能力强;w越小,粒子整体速度越小,有助于群体在当前搜索空间中寻找更优解,即种群局部搜索能力强.在迭代过程中,参数w非线性减小可平衡优化过程中的全局搜索能力和局部搜索能力.对惯性权重w改进如下:
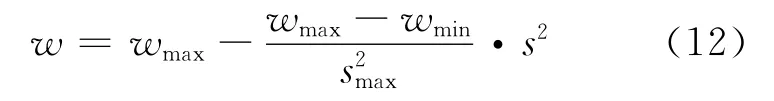
式中:wmax是初始惯性权重,wmin是最终惯性权重,s是当前迭代次数,smax是最大迭代次数.
2.3 粒子初始化
PSO 算法总是采用随机初始化策略,这很难保证初始粒子群的遍历性.混沌运动是非线性系统的一种普遍现象[13].混沌变量有3个主要的特性:遍历性、随机性和对初始条件敏感性,可利用混沌的这些特性来解决粒子初始化问题.
逻辑映射方程如下:
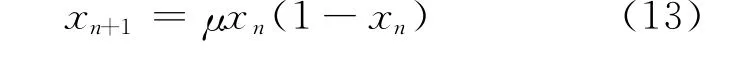
当μ=4且x0{0,0.25,0.50,0.75,1}时,逻辑映射是遍历的.但是在实际应用中,由于不同参数的优化范围是不同的,需要把混沌变量映射到[0,1]来定义解向量的范围.
2.4 过早停滞判断
当pid在M次迭代过程中不变化或者pgd在N次迭代过程中不变化,则认为种群陷入了过早停滞.这说明群体已经或者即将陷入局部最优.M、N的值根据问题的规模和经验提前设定,M、N的值越大说明判断过早停滞的条件越宽松.在PSO 算法中加入过早停滞计算器K1、K2来计算停滞次数.如果Pi或Pg的值与前一次相同,K1或K2的值加1;否则清零.当K1、K2的值达到极限值M、N,重置Pi和Pg使粒子跳出局部最优.
对Pi的改进:
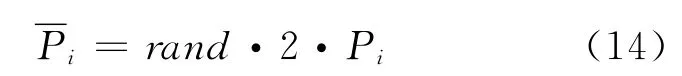
对Pg的改进:
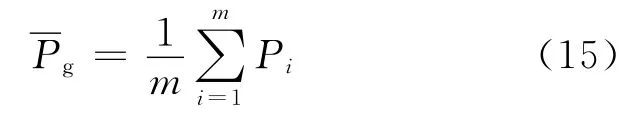
得到改进算法中群体粒子速度和位置方程如下:
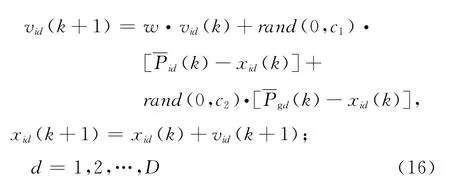
由理论分析可知,新算法可减少无效迭代,大大提高了收敛速度和优化精度.
3 IPSO-SVM 分类器及实验验证
基于改进粒子群优化算法的优点,本文提出用IPSO 方法来优化SVM 的惩罚因子C和核函数宽度σ(IPSO-SVM 分类器),以提高SVM 泛化能力和收敛能力,进而提高分类器精度.
IPSO-SVM 分类器结构图如图1所示.
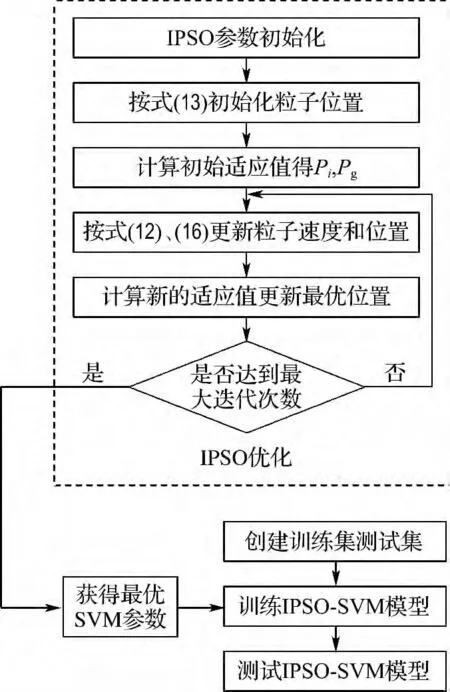
图1 IPSO-SVM 分类器结构图Fig.1 Schematic diagram of IPSO-SVM classifier
为了验证所提出分类器的有效性,本文选择UCI机器学习数据库[14]中的Steel Plates Faults、Ionosphere、Dermatology、Wine和Seeds 5 组数据集对分类器性能进行测试.数据集描述如表1所示.对Dermatology数据集,删除了其含有缺失项的8个样本,余下358个样本.实验中按数据集的成熟度来划分训练数据和测试数据,Steel Plates Faults、Dermatology、Seeds、Ionosphere、Wine数据集的训练数据和测试数据比例分别为4∶1、2∶1、2∶1、1∶1、1∶1.
本文用Matlab2012a软件和LibSVM 工具箱进行仿真实验.选择分类准确率为性能评价指标,也即优化过程中的适应值,径向基函数为核函数,采用5折交叉验证方法[15]以获得具有统计意义 的 实 验 结 果.分 别 用IPSO-SVM、ICPSOSVM[16]、PSO-SVM、GA-SVM 4 种 方 法 对 已 选取的UCI数据集进行分类.其中第二种方法是采用改进的混沌粒子群算法对SVM 参数进行优化,得到了很好的效果并且成功地应用于电子系统故障诊断.4种方法参数设置为m=20,wmax=1.35,wmin=0.35,c1=1.5,c2=1.7,smax=200,M=3,N=6.表2为各方法分类准确率比较,加粗的表示分类准确率最高.
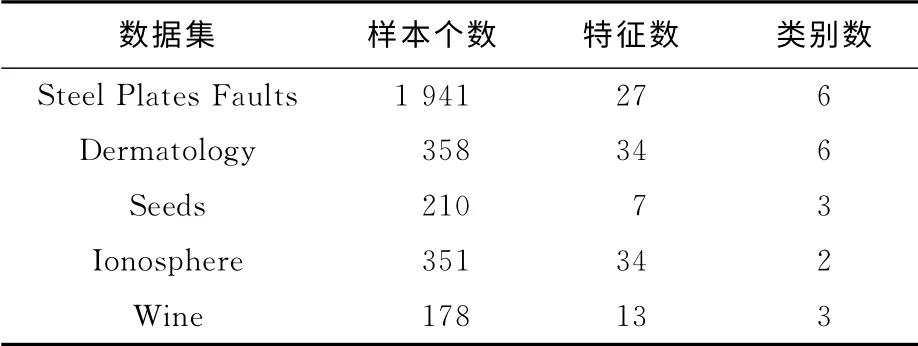
表1 UCI机器学习数据库数据集描述Tab.1 Description of datasets from UCI machine learning repository
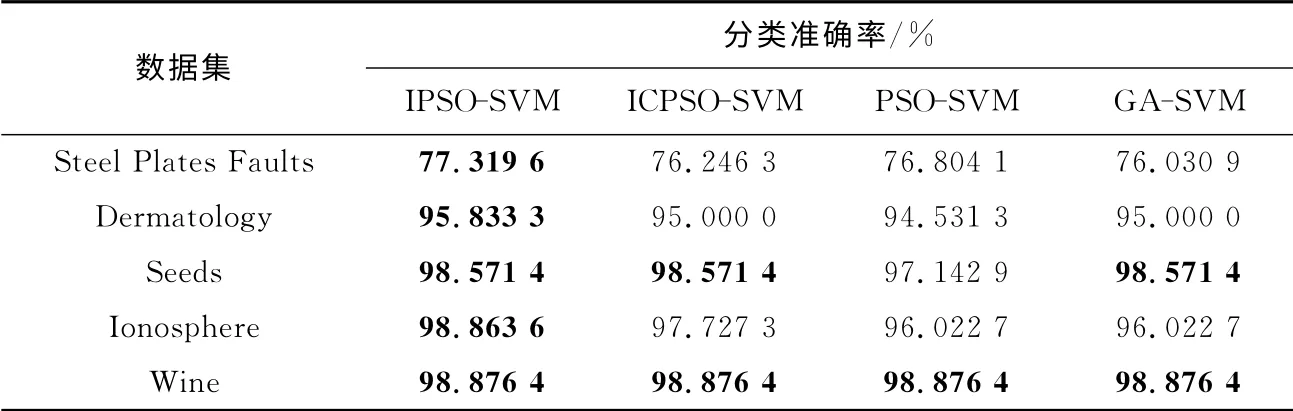
表2 各方法分类准确率比较Tab.2 Classification accuracy comparison of several methods
以上实验结果表明,本文提出的IPSO-SVM分类器有较好的分类效果.对Steel Plates Faults、Dermatology 和Ionosphere数据集,分类准确率均高于其他3 种方法;对较为成熟的Seeds和Wine数据集也与其他方法有相同分类准确率,验证了IPSO-SVM 方法的有效性.
4 地铁牵引控制单元故障诊断
应用某地铁6号线实际数据验证基于IPSOSVM 故障诊断模型的高效性和准确性.
4.1 数据提取与处理
这里的数据提取与处理借助于中国北车研发的维护终端PTU 软件.中央控制单元在地铁运行过程中采集运行数据和故障数据.选取地铁车辆牵引控制单元7种有代表性的故障进行研究,图2是故障数据的提取过程.
本文针对地铁牵引控制单元的7 种典型故障,即1#HSCB跳闸故障、2#电机电流超过2 200A、3#滤波电压超过2 150V、4#逆变器故障、5#牵引电机警告级过温、6#荷载信号故障、7#380V 供电故障进行故障定位,并选取与牵引控制单元有关的14 个数字量和模拟量,即KIC状态、HSCB状态、空转滑行信号、TCU 硬线收到的牵引指令、TCU 硬线收到的所有制动缓解信号、电制动退出信号、无高压状态、逆变器脉冲施加信号、TCU 硬线收到的制动指令、实际牵引电制动力平均值、TCU 硬线收到的PWM 信号、接触网电压、级位、列车速度作为输入特征.
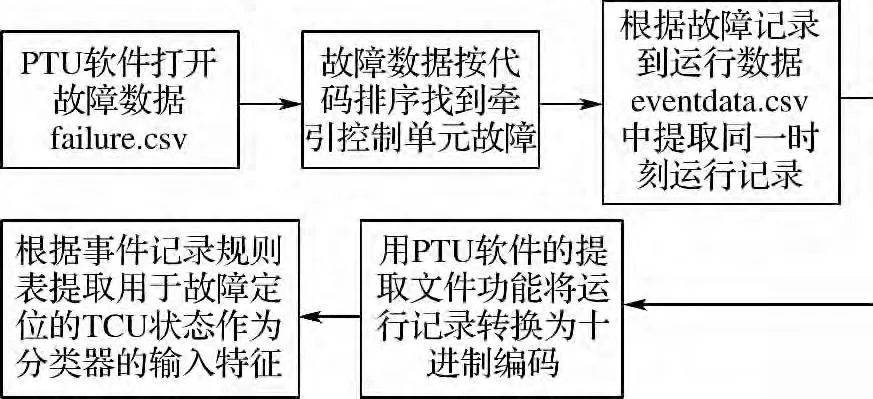
图2 故障数据提取过程Fig.2 Process of failure data extraction
4.2 实验结果及分析
由上述数据提取方法得到271组故障数据并做归一化处理,训练集217组,测试集54组,数据分布如表3所示.
与实验部分相同,这里选择分类准确率为性能评价指标,径向基函数为核函数,5 折交叉验证法估计模型性能.用IPSO-SVM、ICPSO-SVM、PSO-SVM、GA-SVM 4种方法对已选取的数据集做故障分类,参数设置为m=20,wmax=1.35,wmin=0.35,c1=1.5,c2=1.7,smax=200,M=3,N=6,实验结果如表4所示.

表3 训练集和测试集数量分布Tab.3 The number distribution of training and test sets
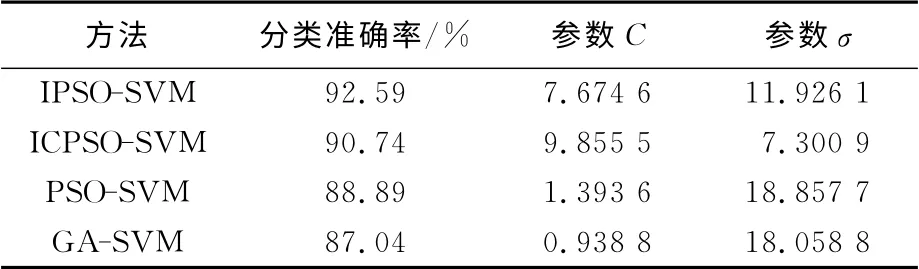
表4 各种方法故障识别率比较Tab.4 Fault detection accuracy comparison of several methods
由表4可知将本文提出的多分类IPSO-SVM方法应用于地铁牵引控制单元,分类准确率有明显提高,同时结果也表明了用改进的粒子群算法优化支持向量机参数是一种有效方法.
5 结 语
支持向量机泛化能力强,处理小样本效果好的特性使其很适用于地铁车辆故障诊断.但是SVM 参数对其模型精度和泛化能力有很大的影响.本文提出了一种改进的粒子群算法来优化SVM 惩罚因子和核函数宽度.在改进算法中,使惯性权重在迭代中逐渐减小,来平衡种群的全局搜索能力和局部搜索能力;使用混沌序列来初始化个体位置,增强了搜索多样性;且在PSO 算法中加入有效识别过早停滞的算法,在一定程度上避免了过早停滞的发生.实验部分证实了IPSOSVM 的有效性.本文以牵引控制单元作为研究对象,但所提出的方法同样适用于地铁车辆其他单元的故障诊断.
[1] Tang T,Zhu Y,Li J,etal.A fuzzy and neural network integrated intelligence approach for fault diagnosing and monitoring [J].IEE Conference Publication,1998(455):975-980.
[2] Kiernan L,Warwick K.Adaptive alarm processor for fault diagnosis on power transmission networks[J].Intelligent Systems Engineering,1993,2(1):25-37.
[3] McDuff R J,Simpson P K,Gunning D.An investigation of neural networks for F-16 fault diagnosis.I.System description [C] //AUTOTESTCON′89.IEEE Automatic Testing Conference.The Systems Readiness Technology Conference.Automatic Testing in the Next Decade and the 21st Century.Conference Record.Philadelphia:IEEE,1989:351-357.
[4] 张代胜,王 悦,陈朝阳.融合实例与规则推理的车辆故障诊断专家系统[J].机械工程学报,2002,38(7):91-95.ZHANG Dai-sheng,WANG Yue,CHEN Zhaoyang.Vehicle-fault diagnosis expert system based on integration of case-based and rule-based reasoning [J].Chinese Journal of Mechanical Engineering,2002,38(7):91-95.(in Chinese)
[5] Pednault E P D.Statistical learning theory[M]//MIT Encyclopedia of the Cognitive Sciences.Cambridge:MIT Press,1998:798-801.
[6] 连光耀,王卫国,黄考利,等.基于粒子群优化算法的测试选择优化方法研究[J].计算机测量与控制,2008,16(10):1387-1389.LIAN Guang-yao,WANG Wei-guo,HUANG Kaoli,etal.Research of optimization method for test selection based on particle swarm optimization algorithm [J].Computer Measurement & Control,2008,16(10):1387-1389.(in Chinese)
[7] Cortes C,Vapnik V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.
[8] Chapelle O,Vapnik V,Bousquet O,etal.Choosing multiple parameters for support vector machines[J].Machine Learning,2002,46(1-3):131-159.
[9] Vapnik V N.An overview of statistical learning theory[J].IEEE Transactions on Neural Networks,1999,10(5):988-999.
[10] Drucker H,WU Dong-hui,Vapnik V N.Support vector machines for spam categorization[J].IEEE Transactions on Neural Networks,1999,10(5):1048-1054.
[11] Gaing Zwe-lee.Discrete particle swarm optimization algorithm for unit commitment[C]//2003IEEE Power Engineering Society General Meeting,Conference Proceedings.Toronto:IEEE,2003:418-424.
[12] van den Bergh F,Engelbrecht A P.A new locally convergent particle swarm optimiser [J].Proceedings of the IEEE International Conference on Systems,Man and Cybernetics,2002,3:94-99.
[13] LIU Bo,WANG Ling,JIN Yi-hui,etal.Improved particle swarm optimization combined with chaos[J].Chaos,Solitons and Fractals,2005,25(5):1261-1271.
[14] Frank A,Asuncion A.UCI Machine Learning Repository [DB/OL].[2014-06-09].http://archive.ics.uci.edu/ml.
[15] LIU Bao-ling,HOU Di-bo,HUANG Ping-jie,et al.An improved PSO-SVM model for online recognition defects in eddy current testing [J].Nondestructive Testing and Evaluation,2013,28(4):367-385.
[16] GUO Yang-ming,MA Jie-zhong,XIAO Fan,etal.SVM with optimized parameters and its application to electronic system fault diagnosis[C]//PHM 2012-2012 IEEE International Conference on Prognostics and Health Management:Enhancing Safety,Efficiency,Availability and Effectiveness of Systems Through PHM Technology and Application,Conference Program.Washington D C:IEEE Computer Society,2012:1-6.

