二维DOA估计中麦克风阵列优化设计

王冬霞，齐 畅，周城旭，牛芳琳

（辽宁工业大学 电子与信息工程学院，辽宁 锦州 121001）

0 引 言

麦克风阵列具有灵活的波束控制、高信号增益、极强的干扰抑制，以及高分辨等优点，已广泛应用于车载系统、视频会议及移动通信等领域［1］.在这些应用中，麦克风阵列系统性能的获得，由空时滤波器系数和阵列方向向量共同决定.然而，现在广泛应用的大多数方法［2－6］中，麦克风阵列拓扑结构固定，只有阵列的空时滤波器系数是待设计的变量，即仅考虑如何改进阵列算法来提高系统性能.此外，相关结果也表明，麦克风数量变化影响着阵列系统响应［1］.但是，很难去判定哪种拓扑结构优于其他结构，或者说没有给出一种可调节的麦克风阵列结构，以改进系统性能、减小系统复杂度.

基于此，本文以二维DOA 估计为应用点，改进遗传算法，将约束阵列空时滤波器系数和决定阵列方向向量的麦克风阵列拓扑结构分开，通过构造由二维MUSIC空间谱函数欧式距离和优化后阵元个数共为变量的适应度函数，DOA 估计精度为停止条件，优化3种不同的麦克风阵列的拓扑结构.

1 阵列优化设计原理

整个阵列优化设计框图如图1所示.

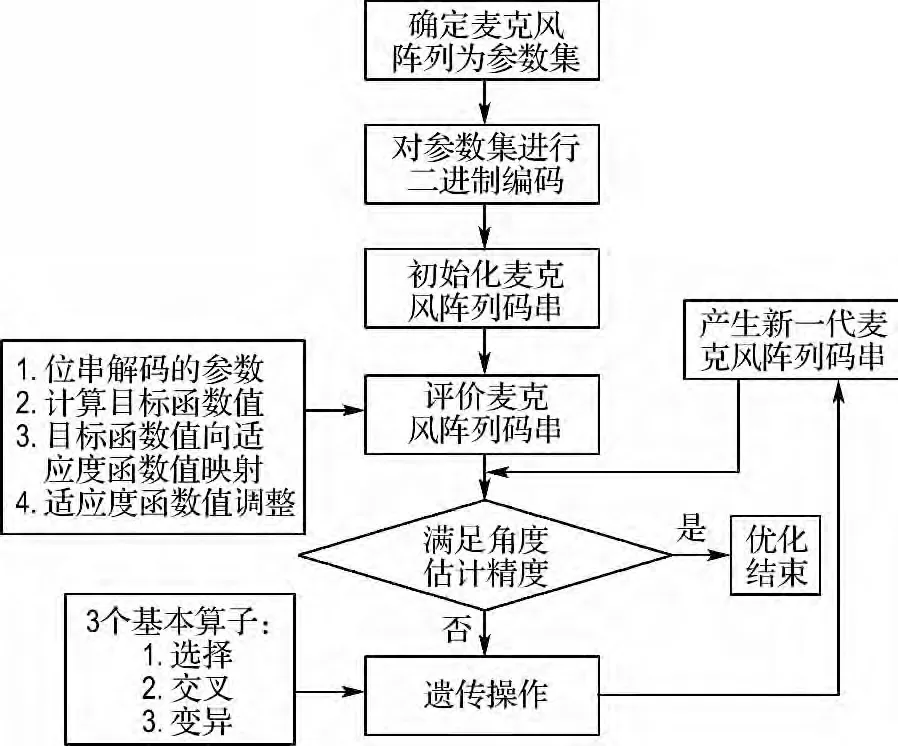
图1 基于遗传算法的麦克风阵列优化设计流程图Fig.1 Flowchart of microphone array optimization design based on genetic algorithm

遗传算法是通过模拟自然进化过程来搜索最优解的一类随机优化算法.它从任一初始种群出发，通过随机选择、交叉和变异操作，一代代不断繁衍进化，产生更适合环境的个体，使群体进化到搜索空间中越来越好的区域，最后收敛到一群最适应环境的个体，即求得问题的最优解.

2 阵列优化设计方法

2.1 参数集

考虑到应用，选择均匀矩形阵（URA）、均匀圆形阵（UCA）和均匀同心圆阵（UCCA）为阵列优化设计中的实际问题参数集.3种阵列的不同空间结构示意图如图2所示.

图2 空间坐标下3种阵列结构Fig.2 Three array configurations in spatial coordinates

2.2 参数集编码

对不同的麦克风阵列结构进行二进制编码，选择其中某一个阵元作为参考阵元，以一定的规律进行编码，1代表此位置有阵元存在，0代表此位置无阵元存在.

2.3 适应度函数

适应度函数值用来评估种群中个体的性能并且指导搜索的方向，即适应度函数的优良决定着优化算法性能的好坏.考虑到优化的目的为二维DOA 估计，故改进遗传算法中的目标函数，对其进行变换，构建由二维MUSIC 空间谱函数数值间的欧式距离和阵元个数共同组成的目标函数.

设有D个源信号入射由M（M＞D）个阵元组成的阵列，则阵列接收信号为

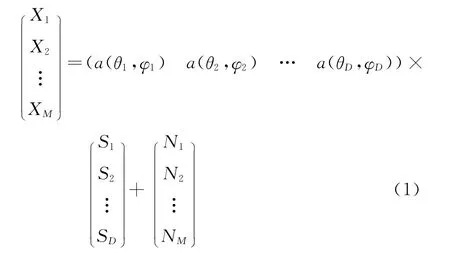
可简写为

式中：A为阵列方向向量，N为阵列接收的随机噪声向量，S为源信号向量.

令R为均匀圆形阵的半径，γ0，…，γM－1分别表示均匀圆形阵中每个阵元与X轴的角度；r1，…，rp分别表示均匀同心圆阵中各个圆环的半径，γ0，…，γMp－1分别表示均匀同心圆阵中每个阵元与X轴的角度.则已确定实际问题参数集中3种阵列的方向向量分别如式（3）、（4）和（5）所示：

式中：λ为声波波长，d为均匀矩形阵的阵元间距，θ、φ分别为信号源的俯仰角和方位角.

对式（2）中X的协方差矩阵进行特征值分解，得到对应于D个大特征值的特征向量构成的信号子空间Us以及M－D个特征向量构成的噪声子空间Un.于是，构造二维MUSIC空间谱函数为

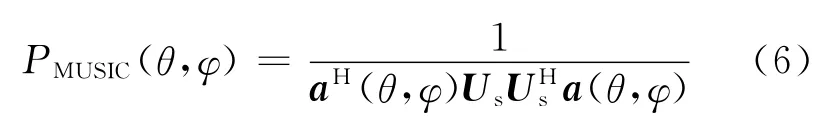
假设PMUSIC1和PMUSIC分别代表优化前后阵列对应求得的二维MUSIC空间谱函数，L为优化后阵列中阵元的总个数，于是，构造目标函数为

式中：α、β为权重，需要满足α＋β＝1.对目标函数进行变换，进而得到适应度函数为

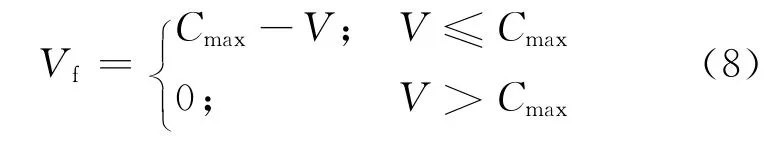
2.4 停止条件

遗传算法停止条件多采用遗传进化代数，其结果有时会在设置的固定遗传代数值之前优化得出最好结果，有时却在设置的固定遗传代数值之后优化得出最好结果，即这样设置停止条件不能保证在满足停止准则时所得结果为最优.

于是，将估计误差代替传统优化设计中采用的遗传进化代数作为停止条件，即这里采用的算法停止条件为，优化前后麦克风阵列对应估计出的语音源的二维来波角度差.

3 仿真实验与结果分析

3.1 仿真环境

实验选取房间大小为7m×5m×4m，混响时间为263 ms，实际问题参数集阵元个数选取16，构成的3种平面麦克风阵列结构如图2所示.

语音源采样频率为8kHz，信噪比为5dB，语音源坐标为（4，3，1.43）m，入射方向为（44.682°，45.000°），停止条件是语言源的二维来波角度差为0.为验证本文方法的有效性，选择了文献［7－9］的方法进行了对比.

3.2 阵列优化设计结果

均匀矩形阵优化前后的DOA 估计性能和阵列优化结构的仿真结果分别如图3和图4所示.

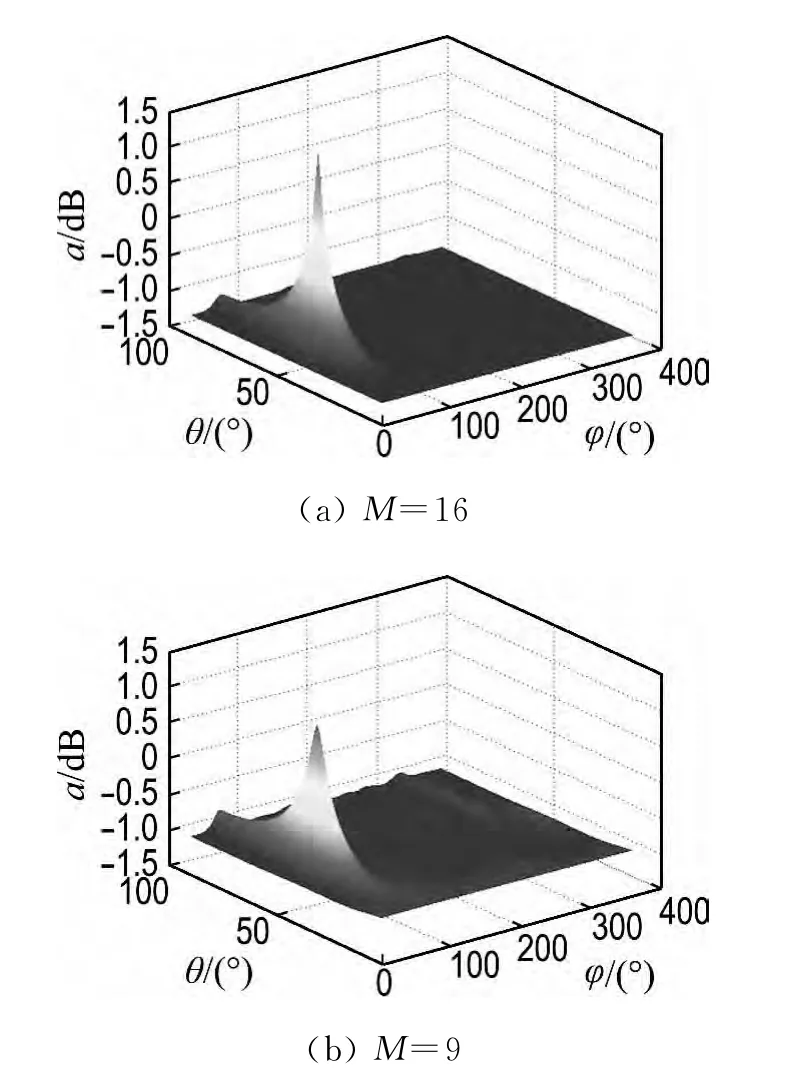
图3 优化前后的均匀矩形阵DOA 估计性能Fig.3 DOA estimation performances of uniform rectangle array before and after optimization

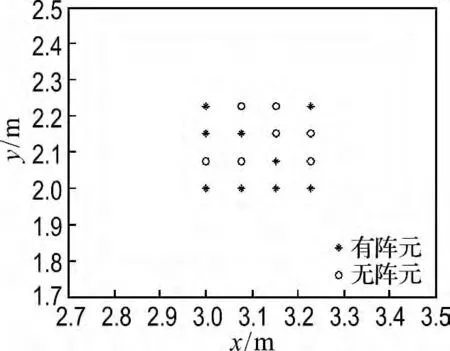
图4 优化前后的均匀矩形阵Fig.4 Uniform rectangle array before and after optimization

均匀圆形阵优化前后的DOA 估计性能和阵列优化结构的仿真结果分别如图5和图6所示.

均匀同心圆阵优化前后的DOA 估计性能和阵列优化结构的仿真结果分别如图7和图8所示.

图3～8表明，在不降低精度的前提下本文方法有效估计出声源二维DOA 位置，且3 种阵列结构的麦克风数目均减少了7个，即达到了阵列优化设计的目的.

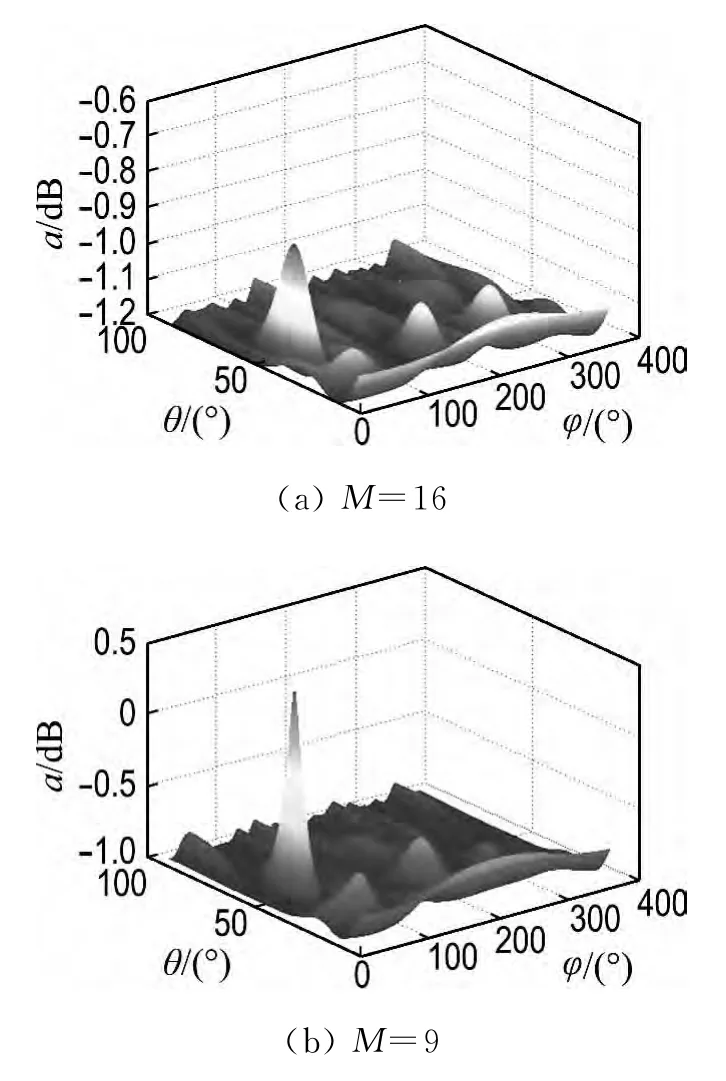
图5 优化前后的均匀圆形阵DOA 估计性能Fig.5 DOA estimation performances of uniform circular array before and after optimization

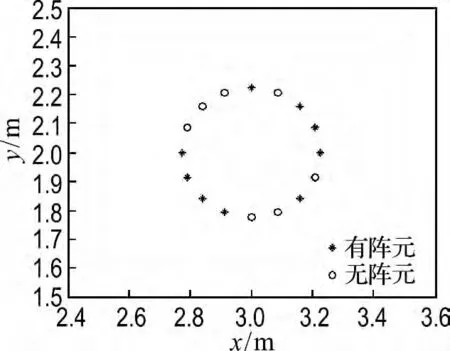
图6 优化前后的均匀圆形阵Fig.6 Uniform circular array before and after optimization

3.3 不同方法的阵列优化结果

实验1 文献［7］中给出了16元均匀正方形阵与随机阵的仿真实验数据，正方形阵中阵元间距均为λ，随机阵阵元随机分布在边长为3λ的正方形内.3 个信号源入射角度分别为（30°，60°），（55°，25°），（25°，25°）.

采用本文方法对上述16元均匀正方形阵进行优化，并对比优化后阵列与文献中正方形阵和随机阵的二维DOA 估计性能.实心点代表有阵元，空心点代表无阵元.各个阵列的阵元位置如图9所示，估计性能比较结果如表1所示.

图7 优化前后的均匀同心圆阵DOA 估计性能Fig.7 DOA estimation performances of uniform concentric circular array before and after optimization

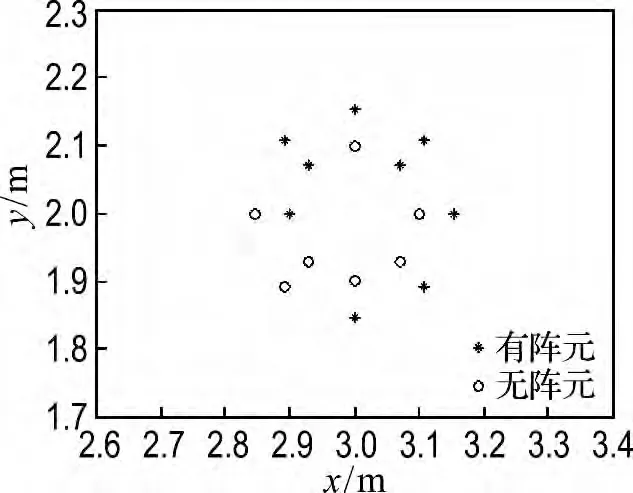
图8 优化前后的均匀同心圆阵Fig.8 Uniform concentric circular array before and after optimization

由表1可知，优化后的10元非均匀正方形阵对应的峰值角度误差高于16元均匀正方形阵和随机阵，但是相差幅度不大，所以在对峰值角度误差要求不是很高的情况下完全可以采用本文方法优化所得的正方形阵，既可满足角度误差要求又可以达到节省阵元的目的.

图9 阵列结构（实验1）Fig.9 Array configurations（Experiment 1）

表1 不同阵形的峰值角度误差（实验1）Tab.1 Peak angle errors of different array configurations（Experiment 1）

实验2 文献［8］中给出了8元矩形阵与任意阵的仿真实验数据，矩形阵各个阵元的坐标为（0，0），（2，0），（4，0），（6，0），（0，2），（2，2），（4，2），（6，2），任意阵各个阵元的坐标为（0，0），（1，0），（3，1），（1，3），（5，3），（2，5），（4，0），（6，0）.3个信号源入射角度分别为（20°，10°），（40°，20°），（30°，70°）.

采用本文方法对上述8元矩形阵进行优化，并对比优化后阵列与文献中矩形阵和任意阵的角度测向性能.各个阵列的阵元位置如图10所示，测向性能比较结果如表2所示.

图10 阵列结构（实验2）Fig.10 Array configurations（Experiment 2）

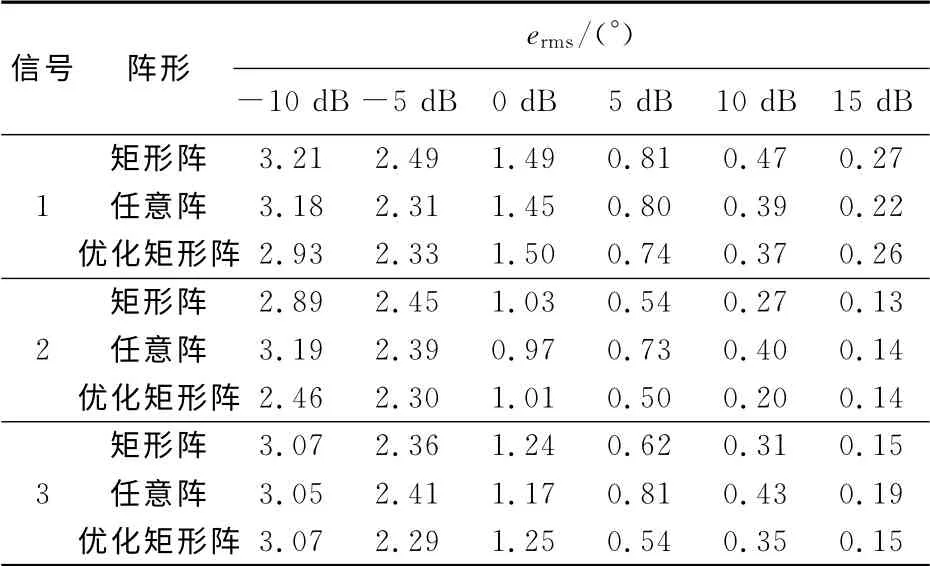
表2 不同阵形的均方根误差（实验2）Tab.2 RMSE of different array configurations（Experiment 2）

由表2可知，对不同的信号源入射角度，从整体趋势上可以看出，在信噪比变化过程中，8元均匀矩形阵的均方根误差要大于任意阵和本文优化后的阵列（非均匀阵列）.3种阵形相比较，优化后阵列的测向精度较好，在低信噪比（－10dB）时，测向性能好于矩形阵和任意阵，并且优化后阵列还节省了2个阵元.

实验3 文献［7］中给出了16元均匀圆形阵与10元半圆形阵的仿真实验数据，均匀圆形阵与半圆形阵的直径均为3λ.3个信号源入射角度分别为（30°，60°），（55°，25°），（25°，25°）.

采用本文方法对上述16元均匀圆形阵进行优化，并对比优化后阵列与文献中均匀圆形阵和半圆形阵的二维DOA 估计性能.各个阵列的阵元位置如图11所示，估计性能比较结果如表3所示.

图11 阵列结构（实验3）Fig.11 Array configurations（Experiment 3）

表3 不同阵形的峰值角度误差（实验3）Tab.3 Peak angle errors of different array configurations（Experiment 3）

由表3可知，优化后的8元非均匀圆形阵对应的峰值角度误差高于16元均匀圆形阵，但是相差幅度不大，与半圆形阵对应的峰值角度误差相等，所以在对峰值角度误差要求不是很高的情况下完全可以采用本文方法优化所得的圆形阵，既可满足角度误差要求又可以达到节省阵元的目的.

实验4 文献［9］中给出了32元均匀同心圆阵与稀疏同心圆阵的仿真实验数据，均匀同心圆阵分为内、外两圈，且各个圆圈上的阵元总数均为16个.

采用本文方法对上述32元均匀同心圆阵进行优化，并对比优化后阵列与文献中均匀同心圆阵和稀疏同心圆阵的性能.各个阵列的阵元位置如图12 所示，性能比较结果如图13 和图14 所示.

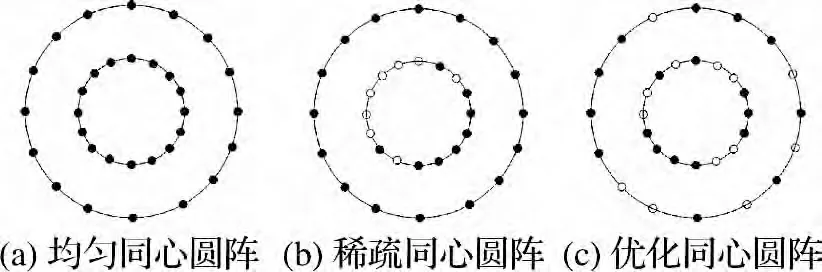
图12 阵列结构Fig.12 Array configurations（Experiment 4）

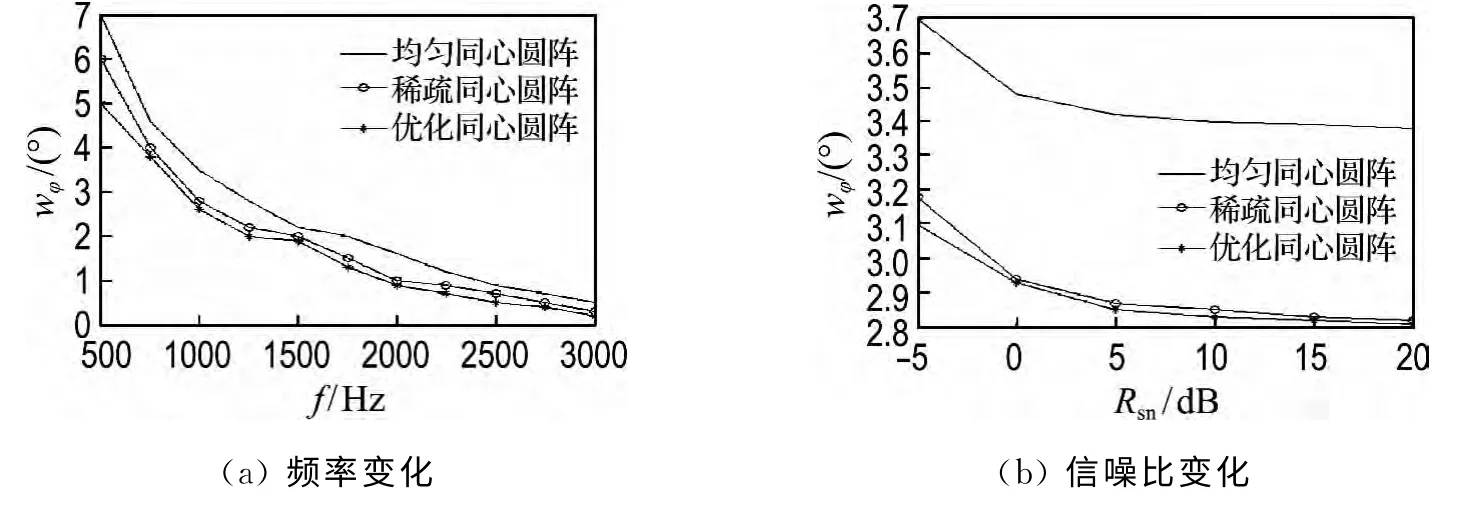
图13 方位角主瓣宽度随频率和信噪比的变化曲线Fig.13 Azimuth mainlobe width variation with frequency and signal－to－noise ratio

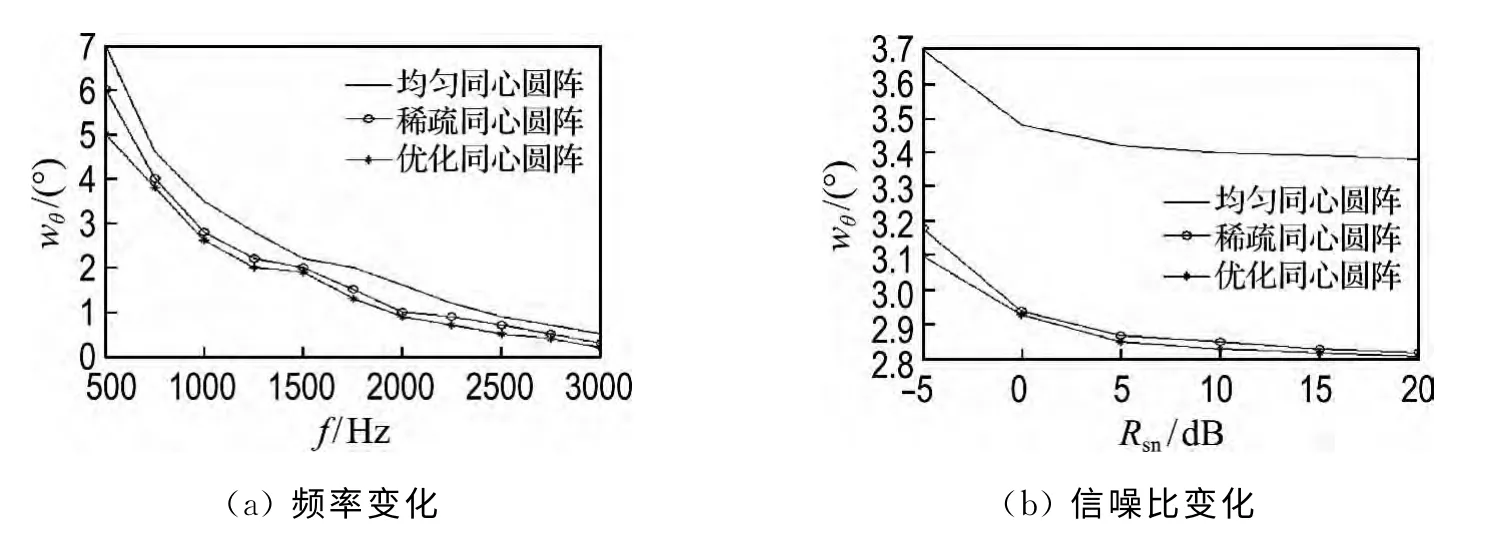
图14 俯仰角主瓣宽度随频率和信噪比的变化曲线Fig.14 Pitch angle mainlobe width variation with frequency and signal－to－noise ratio

由图13和14可知，在保证其他条件相同的情况下，当频率变化范围为500～3 000Hz，信噪比变化范围为－5～20dB 时，相比其他两种阵列，本文方法取得了较好的估计性能.从图中还可以看到，方位角和俯仰角估计性能随参数变化非常相近：即主瓣宽度均随频率的递增而减小，随信噪比的递增而减小.

4 结 语

采用由二维MUSIC空间谱函数欧式距离和优化后阵元个数共为变量构造的适应度函数，语音源来波角度估计精度为停止条件，给出了一种基于改进遗传算法的阵列优化结构设计方法.仿真结果验证了在所选用的实际问题参数集下于取得较好的二维DOA 估计性能的同时，优化后阵列的阵元节省率为43.75%，因此，该方法在阵列系统性能不受影响的前提下，可减少阵元个数、减少计算复杂度，故适用于大孔径麦克风阵列应用领域.

［1］ Jin C T，Epain N，Parthy A.Design，optimization and evaluation of a dual－radius spherical microphone array［J］.IEEE Transactions on Audio，Speech and Language Processing，2014，22（1）：193－204.

［2］ 刁 鸣，王艳温.基于任意形状平面阵列的二维测向技术研究［J］.哈尔滨工程大学学报，2006，27（4）：593－596.DIAO Ming，WANG Yan－wen.Two－dimensional direction estimate technology based on arbitrary plane antenna array ［J］.Journal of Harbin Engineering University，2006，27（4）：593－596.（in Chinese）

［3］ 居太亮，彭启琮，邵怀宗，等.基于任意麦克风阵列的声源二维DOA 估计算法研究［J］.通信学报，2005，26（8）：129－133.JU Tai－liang，PENG Qi－cong，SHAO Huai－zong，etal.Speech source 2D DOA estimation algorithm based on random microphone array［J］.Journal of Communications，2005，26 （8）：129－133.（in Chinese）

［4］ 王冬霞，殷福亮.联合波束形成与谱减法的麦克风阵列语音增强算法［J］.大连理工大学学报，2006，46（1）：121－126.WANG Dong－xia，YIN Fu－liang.Combining beam forming and spectral subtraction for microphone array speech enhancement［J］.Journal of Dalian University of Technology，2006，46（1）：121－126.（in Chinese）

［5］ Kumatani K，McDonough J，Raj B.Microphone array processing for distant speech recognition：From close－talking microphones to far－field sensors［J］.IEEE Signal Processing Magazine，2012，29（6）：127－140.

［6］ 卢海杰，章新华，熊 鑫.非均匀圆阵的方位估计性能［J］.数据采集与处理，2010，25（增刊）：19－22.LU Hai－jie，ZHANG Xin－hua，XIONG Xin.Direction－of－arrival estimation with non－uniform circular array［J］.Journal of Data Acquisition ＆Processing，2010，25（S）：19－22.（in Chinese）

［7］ 刘孝刚，吴世龙.不同阵列流形下的二维DOA 估计性能［J］.舰船电子对抗，2007，30（5）：100－103.LIU Xiao－gang，WU Shi－long.2－D direction of arrival estimation performance under different array manifolds［J］.Shipboard Electronic Countermeasure，2007，30（5）：100－103.（in Chinese）

［8］ 张利强，全厚德，崔佩璋.任意结构平面阵列的测向技术研究［J］.计算机测量与控制，2013，21（4）：886－888.ZHANG Li－qiang，QUAN Hou－de，CUI Pei－zhang.Study of direction estimate for random geometry plane antenna array［J］.Computer Measurement ＆Control，2013，21（4）：886－888.（in Chinese）

［9］ 辛渊博，侯 宏，陈志菲，等.遗传算法用于波达方向估计的圆阵稀疏优化［J］.计算机仿真，2011，28（3）：250－253.XIN Yuan－bo，HOU Hong，CHEN Zhi－fei，etal.Improvement of the DOA performance via circular array optimization by genetic algorithm ［J］.Computer Simulation，2011，28（3）：250－253.（in Chinese）