大骨料混凝土率型内时损伤本构模型
宋玉普,王丽伟,王 浩
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
0 引 言
在实际的大体积混凝土结构中,混凝土的骨料配比多为三级配甚至四级配,且结构在服役期间有时会受到地震等动荷载的作用,这说明大骨料混凝土的动态特性问题值得考虑和研究.近年来全级配大体积混凝土的力学特性被大量学者广泛研究[1-4],相关理论也在逐渐成熟,但目前仍面临很多问题.例如,针对大骨料混凝土的研究多为静态研究,动态研究较少,且动态特性的试验研究并不全面,单轴较多,多轴较少,对于大骨料混凝土本构关系的研究也有待深入,特别是大骨料混凝土动态本构关系.
混凝土作为一种典型的脆性材料,在其受力之初就伴随有不可恢复的变形发生,而且混凝土也是一种典型的率敏感性材料.在动荷载的作用下混凝土的力学特性会发生变化,尤其由于变形反应的滞后性,其裂缝的发展趋势也会减慢.文献[5]中就规定混凝土的动态强度、刚度应较静态有相应幅度的提高.现如今,针对混凝土的力学特点,各国学者已经提出了多种本构模型,但目前没有哪一种模型是公认可以准确描述混凝土材料本构关系的,尤其针对大骨料混凝土动态特性的本构关系研究尚不成熟.
根据以上问题,本文以内时理论和损伤理论为基本框架,同时考虑率效应和骨料粒径的影响,提出大骨料混凝土率型内时损伤本构模型,将混凝土的微裂缝发展问题分离出来用损伤演变方程来刻画.
内时理论最大的特点是在描述材料本构关系的过程中没有用到屈服面的概念,不用遵守流动法则,材料的非线性行为是用内时时间来描述的,这对于没有屈服面的混凝土材料来说非常适用[6].另一方面,同时考虑骨料粒径因素和应变率效应的损伤演变方程,能够很好地描述微裂缝扩展引起的大骨料混凝土刚度退化和动力特性;且模型形式简单、便于计算,非常适用于非线性有限元数值分析.
1 大骨料混凝土率型内时损伤本构模型的建立
本文将大骨料混凝土与小骨料混凝土的力学性能差异主要体现在损伤变量的定义中,而在内时变量的定义中大骨料混凝土与小骨料混凝土完全可以采用同一强化函数.
1.1 有效应力σnij的内时弹塑性关系式
根据文献[7]中给出的内时时间的定义,并综合考虑混凝土材料的特性,可得=dξ/f(ξ),其中ξ为偏内时时间量度,Z为偏内时时间标度为 偏 应 变,a00为反映材料性质变化及耦合效应的函数,f=1/为强化函数.根据文献[8]的分析结果,对混凝土材料有
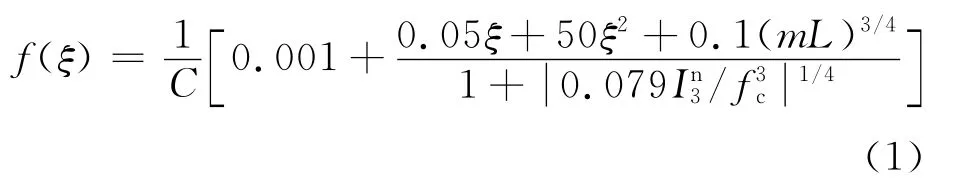
式中:fc为混凝土单轴抗压强度,In3为有效应力的第三不变量为考虑循环的加、卸载系数.
利用耗散材料本构方程的形式不变定律[9],黏塑性本构方程dεij/dt=Delijkmdσnkm/dt+φ/σij可分解成体积应变和偏应变两部分,并用相应的内时时间标度Z来代替真实的牛顿时间t,经简化变换可得

式中:dSnij为偏有效应力增量;G、k为剪切弹性模量和体积弹性模量;φ为加载函数,形式如下:
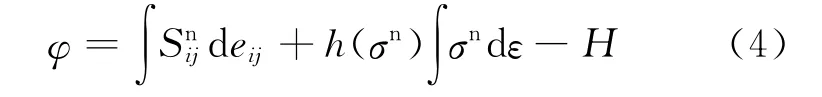


式中

1.2 大骨料混凝土动力损伤演变方程的建立
损伤是一个逐渐累积的过程,损伤演变方程则用来刻画其发展变化的规律.研究表明混凝土动力损伤的演变过程既与应变大小有关,又与应变速率的大小相关,而且混凝土的骨料粒径和试件尺寸也会对损伤造成一定的影响.因此,为了使大骨料混凝土的动态本构模型更真实可靠,以上因素在损伤变量的定义中应有所体现.
1.2.1 损伤演变方程的定义 综合考虑混凝土损伤方程的简洁性和定义的明确性[10],本文采用如下形式的损伤演变方程:
当σkk>0时
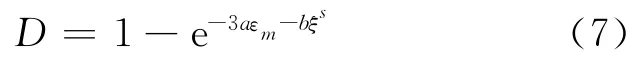
当σkk≤0时

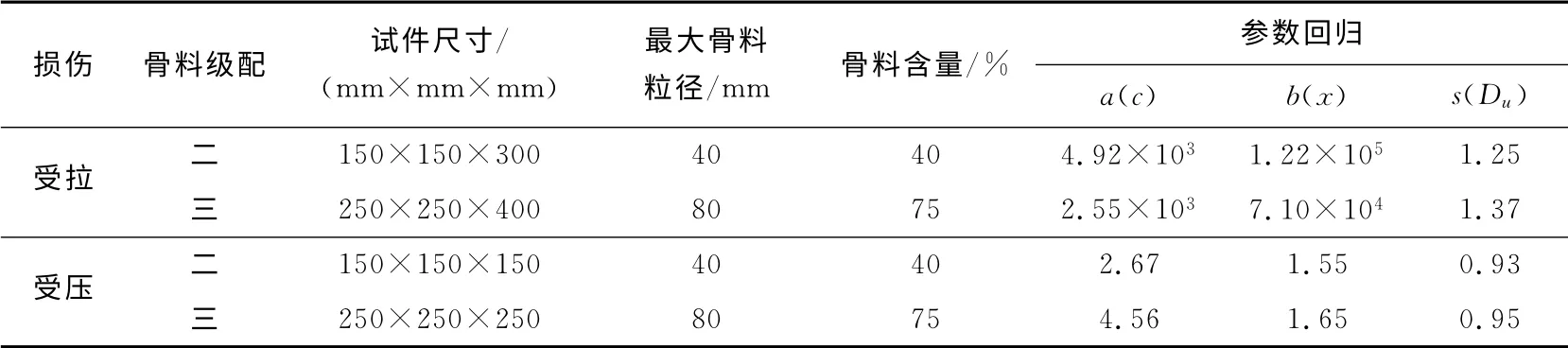
表1 损伤方程参数回归Tab.1 Regression of damage equation parameter
1.2.2 不同级配混凝土的损伤演变方程 不同骨料级配的混凝土应力-应变曲线形状大致相同,所以可以采用同一形式的损伤演变方程,通过对参数取值的改变来反映骨料级配的差异.为了研究骨料级配对于损伤演变方程中待定系数的影响,在此引入骨料影响系数Val/dmax,其中l为不同级配混凝土采用的试件最小尺寸,Va为粗骨料的体积分数,dmax为骨料粒径的最大尺寸,对应各参数取值列于表2.
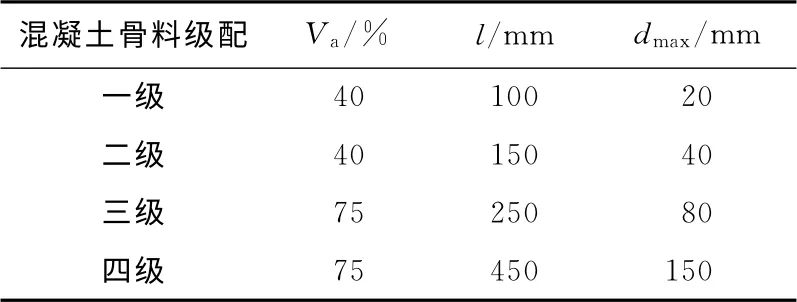
表2 骨料影响系数各参数取值Tab.2 The parameter selection of aggregate influence coefficient
以骨料影响系数Val/dmax为自变量,根据不同级配混凝土试验数据可相应得出e、εm、ξ、D、D′,则可回归出损伤方程中各参数值,列于表1.1.2.3 考虑率效应的动态损伤 混凝土的率敏感性体现在随着应变率的增加,混凝土的强度和刚度都会相应提高,但应力-应变曲线的大致形状不会改变.本文根据峰值点处动力对静力情况的放大关系,引入一个形状函数来构建动力损伤本构模型[11],从而把静态模型推广到动态.
根据大骨料动态试验拟合结果,以单轴动态拉伸为例,取大骨料混凝土的动态单轴拉伸强度、变形、刚度表达形式如下:
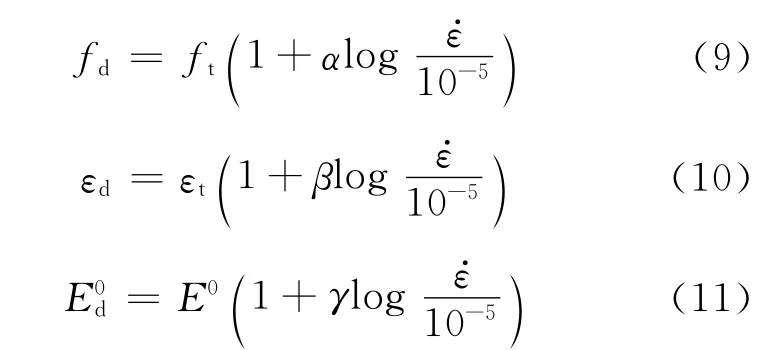
式中:fd、εd、E0d分别为大骨料混凝土动态单轴拉伸强度、相应于动态单轴拉伸强度的拉伸应变和弹性模量,ft、εt、E0分别为对应的拟静态值,为加载速率,α、β、γ可由大骨料试验数据拟合得到,本文取拟静态加载速率为10-5/s.
由损伤变量的物理意义可知

式中:Eft、Efd分别表示拟静态加载速率下和任意加载速率下的峰值割线模量.由式(11)和式(12)可得

当E取为峰值点的割线模量时,对应的损伤定义为峰值点损伤Df,由损伤变量的物理意义可知,Dfd=1-Efd/E0d,Df=1-Eft/E0,经变换可得下式:

式(14)反映了峰值点处损伤随着加载速率变化的规律.
如图1所示,CD线为不同应变率下混凝土峰值点的连线,这条曲线上的损伤值随应变率的变化规律如式(14)所示.根据试验结果,可认为在不同的加载速率下单轴拉伸应力 -应变曲线在0.5ft以前为直线段.AB线为不同应变率下直线和曲线相交处的连线,EF为完全破坏点所连成的线.从CD线与AB线之间的下降段和CD线与EF线之间的上升段,任意一点受应变率变化影响的损伤,其变化规律受到曲线形状的影响.对于这种影响假定引入一个形状函数λ(ε,ε·,10-5)来反映曲线形状对于非峰值点损伤随应变率变化的规律,即

将式(15)变形可得动态受拉损伤变量的演化方程如下:

式中:Ds表示加载速率为10-5/s时的损伤度,可以近似认为是一种静态加载过程如式(13)所示.从图1中可以看出,不同应变率下的应力 -应变曲线的上升和下降段的形状大致相同,因此为了简化计算过程,形状函数λ(ε,10-5)可参考《混凝土设计规范》(GB 50010—2010)中给出的混凝土受拉、受压曲线方程,在3个控制点处根据试验数据做出相应调整.

图1 不同应变率下应力-应变曲线相对位置关系Fig.1 The position relation between stress-strain curves under different strain rates
不同应变率下的受压应力-应变曲线,可认为在0.3fc以前为直线段.根据大骨料多轴动态强度试验所得的数据,可将以上动态损伤本构模型推广到单轴动态压缩和多轴动态情况,其形式和推导过程可仿照单轴情况,本文在此不再复述.
将式(16)代入式(7)、(8)可得
当σkk>0时

当σkk≤0时

其中参数a、b、s和c、x、Du前面已确定.
2 模型验证
运用Fortran语言把本文提出的大骨料混凝土率型内时损伤本构模型编制成非线性有限元程序,并把它嵌入到有限元分析软件ABAQUS中,数值模拟大骨料混凝土试件的受力反应,并与试验结果进行比较,来验证本文编制本构模型的可靠程度.数值模拟中所有混凝土采用八节点等参单元,大骨料混凝土材料参数取为fc=19.29 MPa,E=27.6GPa,μ=0.19.
本文选取了具有代表性的单轴拉伸、单轴压缩、双轴压压和三轴拉压压的应力-应变曲线来进行比较[12].其中,图2、3分别为单轴受拉、受压情况下试验数据和数值模拟结果的比较;图4为应力比为0.25∶1的双轴压缩试验数据和数值模拟结果的比较,这里设压应变为正,拉应变为负;图5为应力比为0.2∶-1∶-1的三轴拉压压试验数据和数值模拟结果的比较,由于相关的试验数据只有极限拉应力-应变曲线,本文三轴数据只比较了一个方向上的曲线.
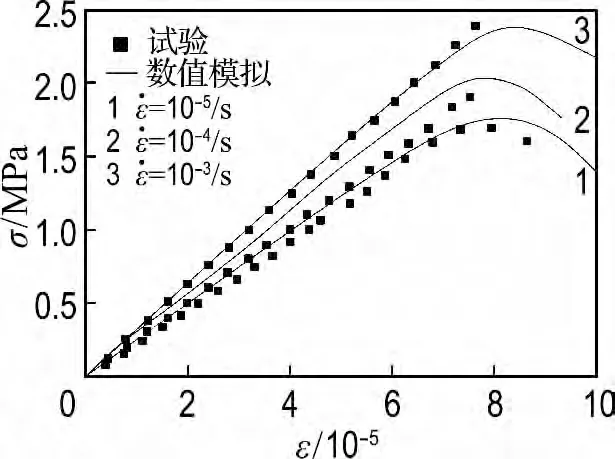
图2 单轴拉伸试验结果比较Fig.2 Contrast of uniaxial tension results
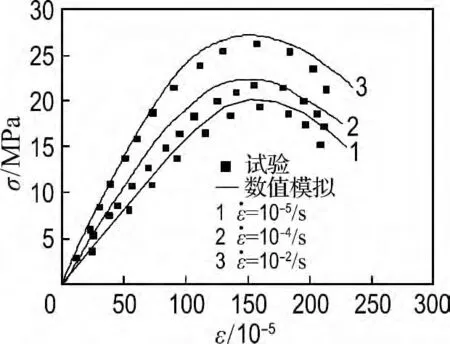
图3 单轴压缩试验结果比较Fig.3 Contrast of uniaxial compression results
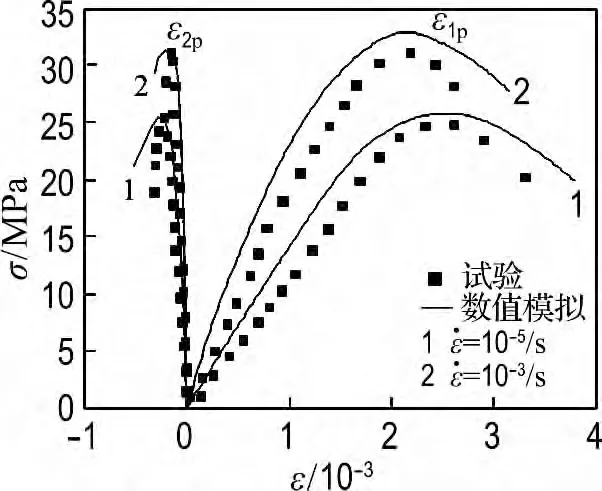
图4 双轴比例加载试验结果比较Fig.4 Contrast of biaxial proportional loading results
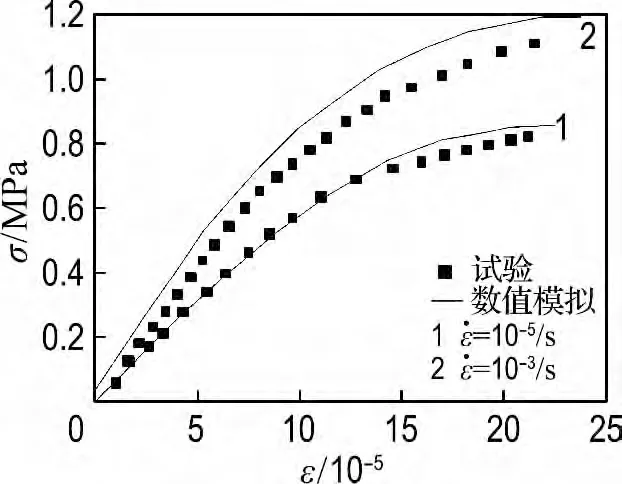
图5 三轴比例加载试验结果比较Fig.5 Contrast of triaxial proportional loading results
由图2、3可知无论是单轴受拉情况下还是单轴受压情况下,本文模型与试验结果都吻合较好,能够很好地反映出随着应变率的提高,混凝土的强度、弹性模量和峰值应力处应变也随之略有提高的规律.由图4和5可知,在双轴比例加载及三轴比例加载情况下,模拟结果虽然与试验结果略有偏差,但误差在允许范围内,能够很好地反映出大骨料混凝土强度在双轴及三轴动态荷载作用下随应变率的增加而提高的特性,且在三轴拉压压应力比情况下,试件所能承受的拉应力小于单轴抗拉强度.
3 拱坝非线性地震反应分析
拱坝这类大体积水工结构,在施工过程中为了节约成本往往选用大骨料混凝土.而数值模拟分析中所建立的模型,材料参数则多采用湿筛小骨料混凝土的试验数据,并且在分析中往往没有考虑到应变率对于混凝土力学性能的影响这一重要因素.所以数值模拟结果和坝体在实际荷载作用下的力学响应可能会有很大偏差,这会使结构在正常工作时处于危险状态或者对于结构进行的评估设计过于保守.
本文将考虑了大骨料因素和率效应的混凝土本构模型用于拱坝的地震响应分析中,并分别和不考虑大骨料因素和率效应的模型进行对比,来验证本文提出本构模型的实际应用价值.在整个计算过程中考虑了拱坝的自重和静水压力的影响,动荷载有地震荷载.建立拱坝模型如图6所示,坝高55.5 m,为单曲等厚拱坝,共划分为4 448个单元,有22 404个节点.模型采用的计算参数为坝体弹性模量25×1010Pa,泊松比0.2,大骨料混凝土抗压强度19.3MPa,湿筛混凝土抗压强度24.5MPa,质量密度2 500kg/m3.动态计算时采用无质量地基模型,质量密度为0,地震波的输入采用x方向的地震波,如图7所示,输入最大位移为0.474m 的地震动位移.

图6 拱坝模型Fig.6 Model of arch dam
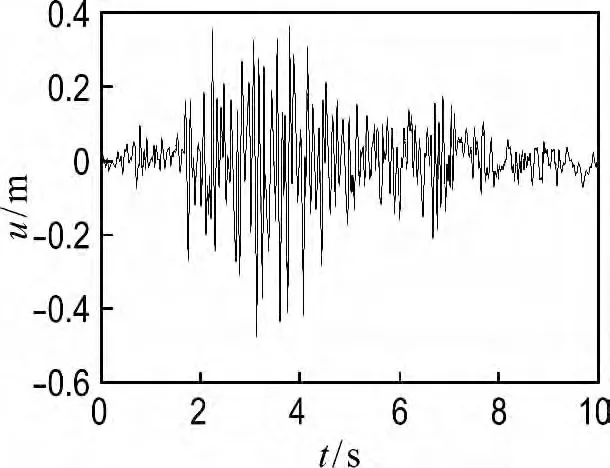
图7 地震波时程曲线Fig.7 History time curve of earthquake wave
本文计算了3个模型在自重、静水压力、地震荷载作用下的动力反应:模型1,小骨料内时本构率无关模型;模型2,大骨料内时本构率无关模型;模型3,大骨料内时本构率相关模型.
将各个模型的第一主应力和第三主应力列于表3中.

表3 拱坝最大主应力Tab.3 Maximal principal stress of arch dam
对比分析模型1、2可知,模型2的第一主应力比模型1 降低了27.82%,第三主应力两模型基本相同,这是由于拱坝的压应力具有较大的容许值,而拉应力区进入了塑性状态,因而拉应力发生了较大的重分布.由第一主应力可以看出大骨料混凝土的强度要比相应湿筛混凝土的强度低.在进行大坝数值分析时,如果仍继续采用小骨料的试验数据,那么分析结果会偏于危险,因此在对采用大骨料混凝土作为坝体材料的大坝进行数值分析时,必须要考虑到大骨料这一骨料粒径的影响因素,分析结果才更安全可靠.
对比分析模型2、3可知,当考虑了混凝土的率相关性后,模型3比模型2的最大拉应力增加了26.04%,最大压应力增加了1.68%,这主要是因为压应力区进入塑性的部分较少,因而应力重分布不明显,应变率效应不明显.拉应力区进入塑性部分较多,应变率效应更加明显,这也说明考虑率相关性后,由于混凝土的屈服强度增加了,混凝土的抗拉强度也相应地提高了,因此在拉应力区的应力也随之相应地提高了.证明了把拉应力作为拱坝设计和抗震安全性评价的控制应力的结论.同时也说明了应变率对结构动态性能的影响这一因素在结构动态分析中也应得到充分的重视.
表3中以地震响应的最终状态来分析说明骨料粒径和应变率效应对于大坝力学特性的影响,而在整个地震响应过程中,某一瞬时坝体第一主应力在同一时刻不同模型中的大小有较大的不同,本文以1.6s时刻,模型2、3的最大第一主应力和第三主应力来说明,如表4所示.

表4 最大主应力对比Tab.4 Contrast of maximal principal stress
可以看出考虑混凝土的率相关性后,由于混凝土的强度增加了,模型3的坝体第一主应力相应减小了,第三主应力相差不多,这是由于在承受动荷载的瞬间,因为大坝考虑率效应后模型屈服强度增加了,所以在某一瞬时相同的受力情况下压应力区分担的荷载增加,这样拉应力就相应降低.这说明采用大骨料混凝土率型内时本构模型进行的模拟中,结果与实际坝体受动力荷载的情况更加接近,而且采用此本构模型进行分析设计,由于考虑率效应后混凝土强度提高,能够很好地节省混凝土材料,使工程设计更加经济合理.
4 结 论
(1)本文模型数值模拟结果与大骨料多轴动态试验数据吻合较好,无论是单轴还是多轴情况,都能够反映出大骨料混凝土的强度、刚度、峰值应变随着应变率的提高而相应提高的动态特性.
(2)对拱坝进行动力非线性分析结果表明,考虑大骨料因素后作为控制应力的拉应力明显降低,在大骨料的基础上考虑率效应后混凝土的强度会随之提高,表现出大骨料混凝土的动态特性,说明本文本构模型具有很强的实用价值.
[1] 邓宗才,李庆斌,傅 华.人工骨料全级配大坝混凝土的拉压力学性能[J].水利学报,2005,36(2):214-218.DENG Zong-cai,LI Qing-bin,FU Hua.Tensile and compressive behaviors of full grade concrete made of crushed coarse aggregate[J].Journal of Hydraulic Engineering,2005,36(2):214-218.(in Chinese)
[2] 朱尔玉.大骨料混凝土多轴强度理论及本构关系的试验研究[D].大连:大连理工大学,1996.ZHU Er-yu.Large aggregate concrete multiaxial strength theory and the study of constitutive relationship [D].Dalian:Dalian University of Technology,1996.(in Chinese)
[3] 王怀亮,宋玉普,曲晓东,等.大坝原级配混凝土在双轴拉压及三轴拉压压受力状态下的试验研究[J].土木工程学报,2007,40(7):104-110.WANG Huai-liang,SONG Yu-pu,QU Xiao-dong,etal.Experimental study of mass concrete under biaxial compression-tension and triaxial compression-compression-tension stresses [J].China Civil Engineering Journal,2007,40(7):104-110.(in Chinese)
[4] 王怀亮,宋玉普.定侧压下大坝原级配混凝土强度和变形试验研究[J].大连理工大学学报,2010,50(3):393-398.WANG Huai-liang,SONG Yu-pu.Research on strength and deformation properties of mass concrete under compressive loading with constant lateral stress[J].Journal of Dalian University of Technology,2010,50(3):393-398.(in Chinese)
[5] 中华人民共和国国家经济贸易委员会.DL 5073—2000 水工建筑物抗震设计规范[S].北京:中国电力出版社,2001.The State Economic and Trade Commission of the People′s Republic of China.DL 5073-2000 Specifications for Seismic Design of Hydraulic Structures[S].Beijing:China Power Press,2001.(in Chinese)
[6] 宋玉普,赵国藩.混凝土内时损伤本构模型[J].大连理工大学学报,1990,30(5):577-584.SONG Yu-pu,ZHAO Guo-fan.Endochronic damage constitutive model for concrete[J].Journal of Dalian University of Technology,1990,30(5):577-584.(in Chinese)
[7] Valanis K C.A theory of visco-plasticity without a yield surface.Part 1.General theory [J].Archiwum Mechaniki Stosowane,1971,23:517-551.
[8] Bazant Z P,Shieh Ching-long.Hysteretic fracturing endochronic theory for concrete[J].Journal of the Engineering Mechanics Division,1980,106(5):929-950.
[9] Valanis K C.On the substance of Rivlin′s remarks on the endochronic theory[J].International Journal of Solids and Structures,1981,17(2):249-265.
[10] Frantziskonis G,Desai C S.Constitutive model with strain softening[J].International Journal of Solids and Structures,1987,23(6):733-750.
[11] 刘 军.混凝土损伤分析及其工程应用[D].大连:大连理工大学,2004.LIU Jun.The damage analysis of concrete and its engineering application [D].Dalian:Dalian University of Technology,2004.(in Chinese)
[12] 尹 翠.大骨料混凝土双轴应力状态下的动态性能试验研究[D].大连:大连理工大学,2013 YIN Cui.Experimental study on the behavior of large aggregate concrete under dynamic biaxial stress states [D].Dalian:Dalian University of Technology,2013.(in Chinese)

