非线性半定规划的雅可比唯一性定理
高 婕,张宏伟,张立卫
(大连理工大学 数学科学学院,辽宁 大连 116024)
0 引 言
最优化问题的扰动分析是非常重要的专题,在数值算法实现的稳健性分析和双层规划的理论研究中起着非常重要的作用.目前,扰动分析的研究已经取得了丰富的进展,比如近年来国际优化领域出版了关于变分分析、扰动分析、非光滑方程和互补与变分不等式的著名专著[1-4],在这些专著中最优化的扰动理论都不同程度地被给予关注.文献[5]详细介绍了非线性规划的扰动分析结果,文献[2]详细介绍了一般最优化问题的扰动分析结果.
追溯到扰动分析的早期工作,讨论的问题非常特殊,如讨论问题的函数是二次连续可微的,扰动后的函数关于决策变量和扰动参数也是二次连续可微的,在此情况下,扰动问题解的存在性、连续性和微分性质.Fiacco等[6]在1968 年对非线性规划在这种情况的扰动分析给出讨论,提出了著名的雅可比唯一性条件(Jacobian uniqueness conditions).对非线性半定规划而言,类似的雅可比唯一性条件是什么样的条件,由此条件出发得到什么样的稳定性理论,还没有文献涉及,本文讨论这些问题.
1 雅可比唯一性定理
考虑非线性半定规划问题:
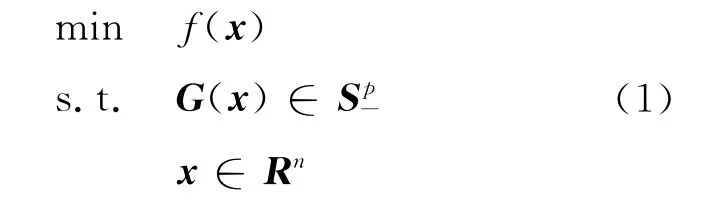
其中f:Rn→R 与G:Rn→Sp是二次连续可微函数和映射.式(1)的Lagrange函数定义为
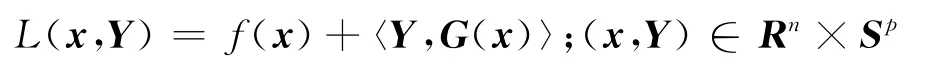
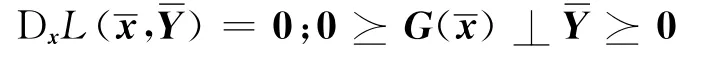
式(1)在稳定点处的临界锥C)定义为

设是可行点,所谓雅可比唯一性条件是指如下的4个条件成立:
(1)存在∈Sp满足
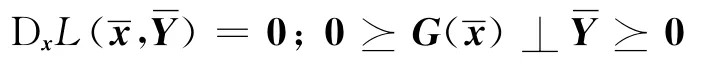
(2)约束非退化条件在处成立,即
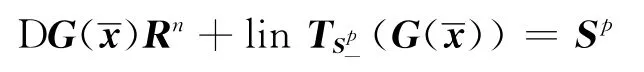
(3)严格互补条件成立,即
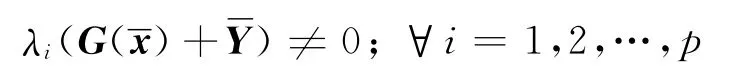
(4)二阶充分条件成立,即
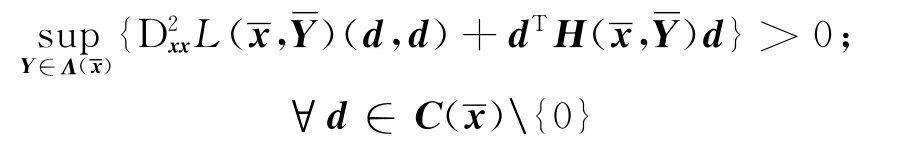
其中
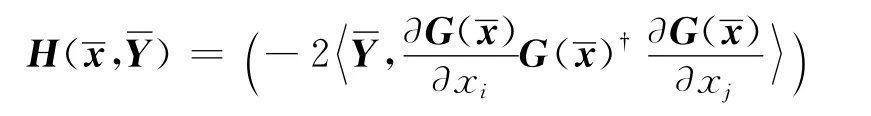
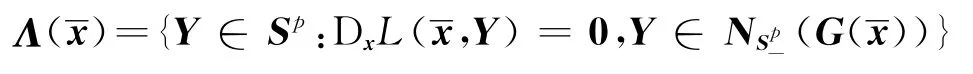
定理1 设f:Rn→R与G:Rn→是二次连续可微函数和映射,Φ是式(1)的可行集合,∈Φ满足条件(1)~(4),则映射
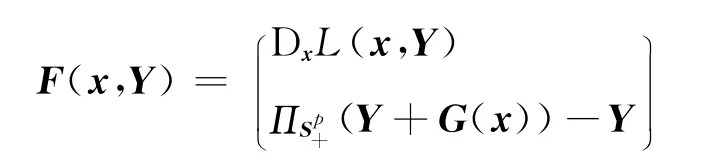
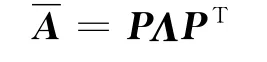
其中Λ=diag{λ1,…,λp},λ1≥… ≥λp是的p个 特 征 值,P∈Rp×p是正交矩阵,P=(q1…qp),则映射在处沿H∈Sp的方向导数为
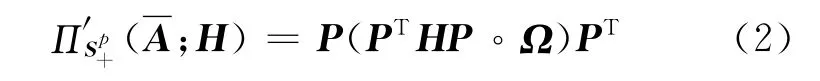
其中。为矩阵的Hadamard乘积运算,Ω∈Sp的元素Ωij定义为
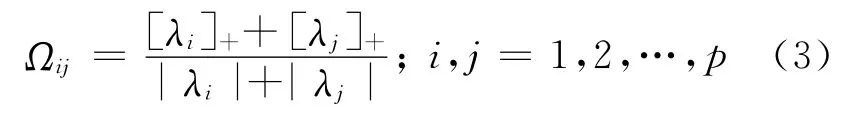
于是,映射F在处沿(Δx,ΔY)的方向导数为
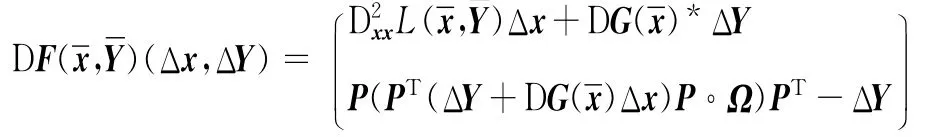
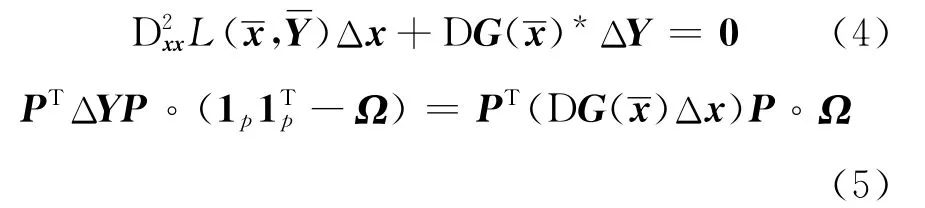
引入指标集合
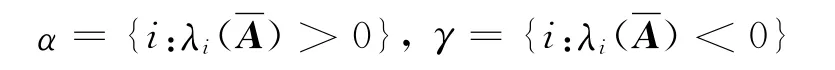
则
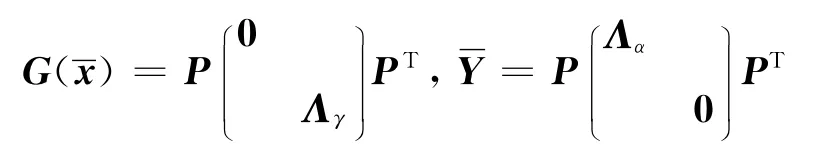
记Pα=(pi:i∈α),Pγ=(pi:i∈γ).由于严格互补条件成立,临界锥C()可以表示为
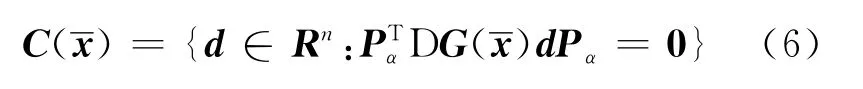
把Ω表示为
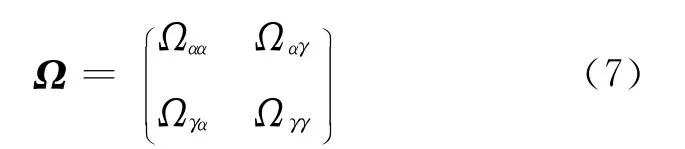
则Ωαα=1|α|1T|α|,Ωγγ=0|γ|×|γ|,
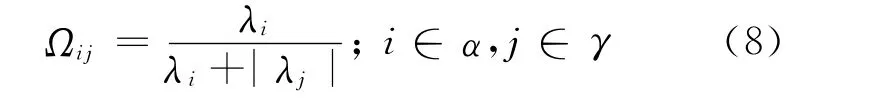
由式(5)可得
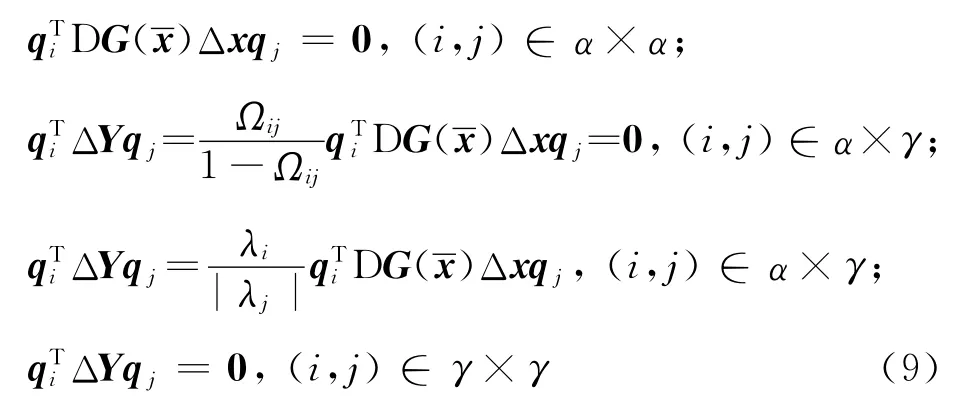
用Δx与式(4)两边的向量做内积,并由式(9)可得
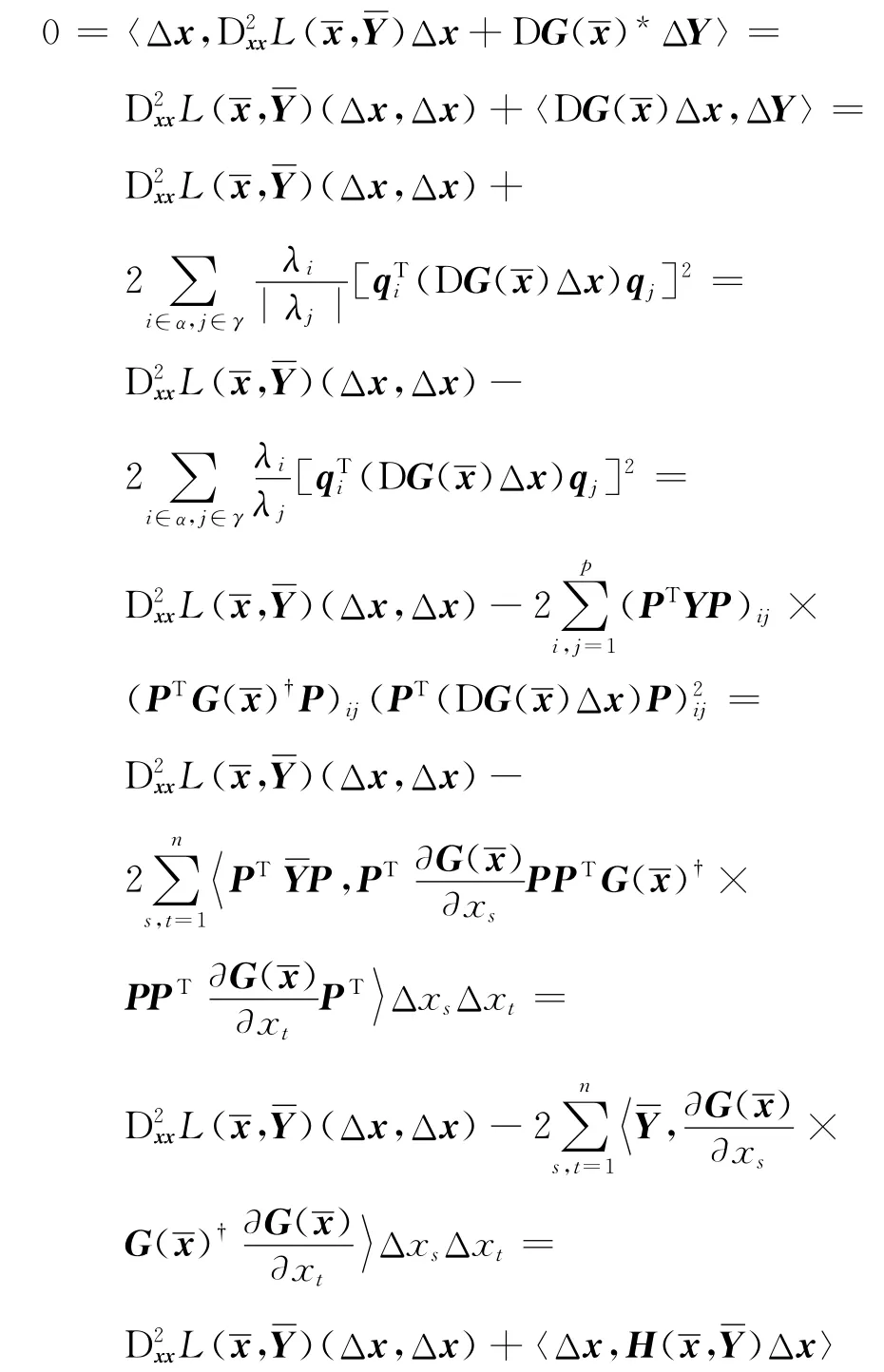
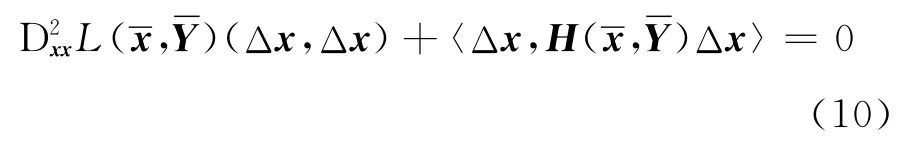
即根据在条件(3)成立的前提下临界锥的表达式(6),式(9)的第一式意味着Δx∈C(),因此由二阶条件和式(10)可推出Δx=0.由式(4)可得
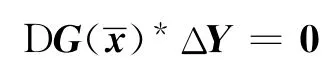
由此结合PTαΔYPγ=0与PTγΔYPγ=0以及约束非退化条件(2),得到PTαΔYPα=0,于是得到ΔY=0.证毕.
在雅可比唯一性条件成立的前提下,可以进行式(1)的稳定性分析.
命题1 考虑如下的扰动问题:
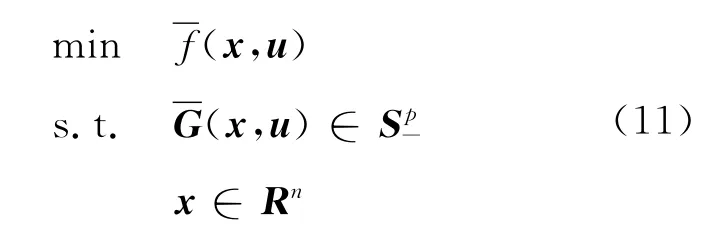
证明 定义映射
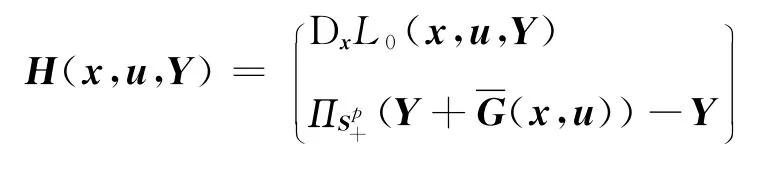
其中
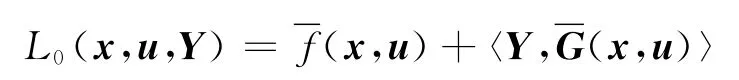
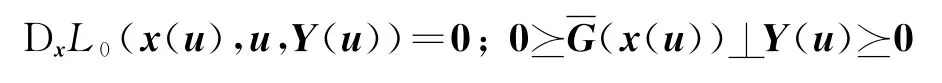
由(x(·),Y(·))的连续性,对u∈B(0,ε),式(11)在x(u)处的约束非退化条件成立,严格互补条件成立.
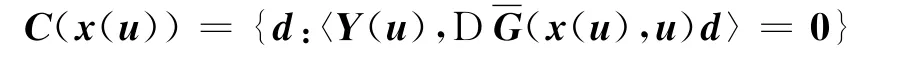
在u=0处连续(在变分分析的集值映射连续的意义下)以及
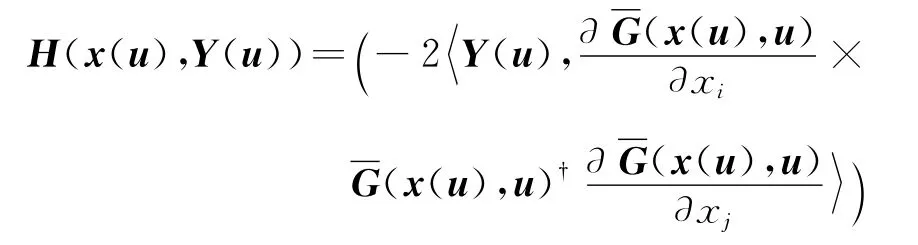
在u=0处的连续性,对充分小的ε>0,u∈B(0,ε)时,
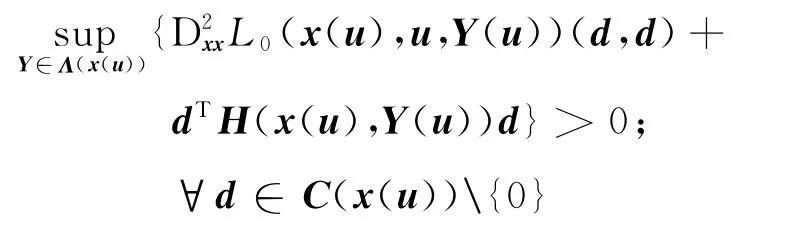
即在(x(u),Y(u))处,式(11)的二阶充分最优性条件成立,因此x(u)是式(11)满足二阶增长条件的局部极小点.
作为命题1的应用,考虑扰动问题:
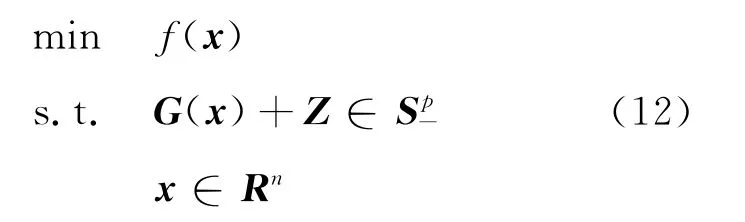
其中Z∈Sp.式(12)的最优值函数被称为扰动函数,记为ν(Z).
定理2 设f:Rn→R与G:Rn→Sp- 是二次连续可微函数和映射,∈Φ满足条件(1)~(4),则
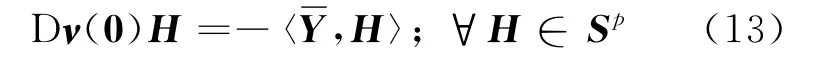
证明 由命题1,存在ε>0,唯一的连续可微映 射(x,Y)满足对任意的Z∈B(0,ε),(x(Z),Y(Z))满足式(12)的KKT 条件,即
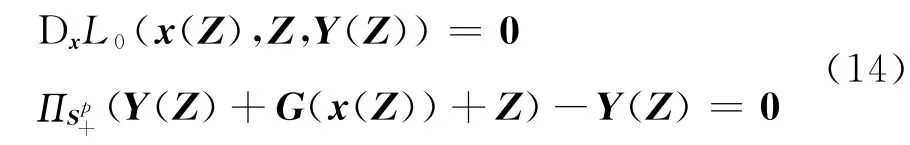
其中
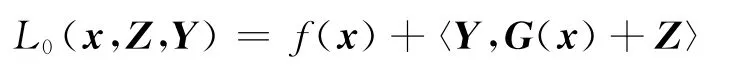
由式(14)的第二式得
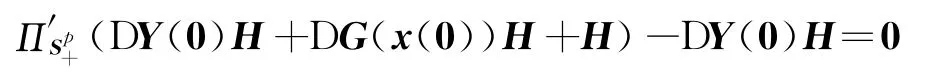
即
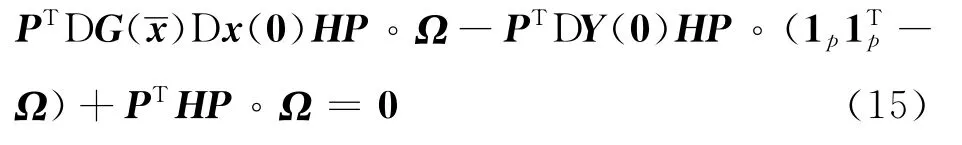
由于(1p1Tp-Ω)αα=0|α|×|α|,Ωαα=1|α|1|α|T,由式(15)得
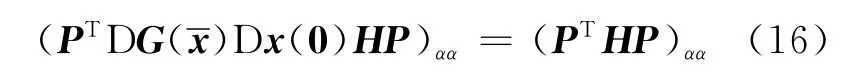
根据
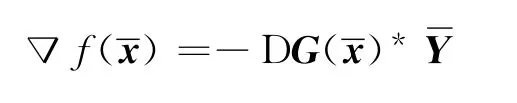
和式(16)得
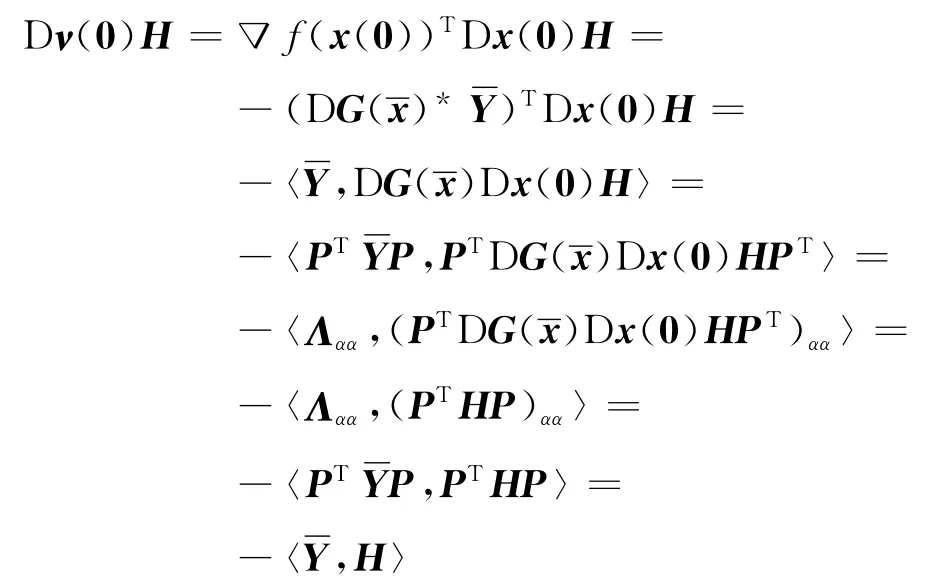
得到结论.
2 一类双层规划的最优性条件
考虑如下的双层优化问题,上层优化问题定义为
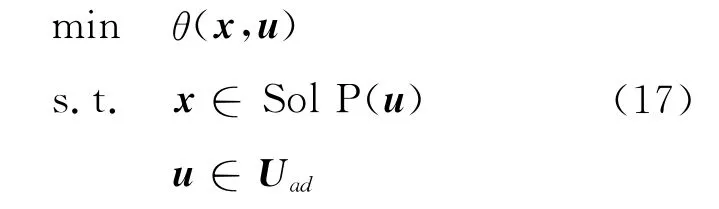
下层为问题P(u),定义如下:
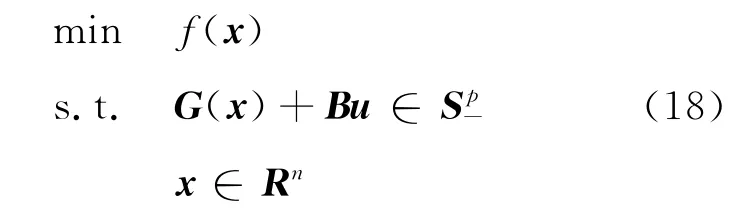
其中θ:Rn×Rm→R是连续可微函数,UadRm是非空闭凸集合,Sol P(u)表示问题P(u)的最优解集合,B:Rm→Sp是一连续的线性算子.
对任何u∈Rm,设在(x(u),Y(u))处问题P(u)的雅可比唯一性条件成立,由命题1 得,(x(u),Y(u))是二次连续可微映射,满足
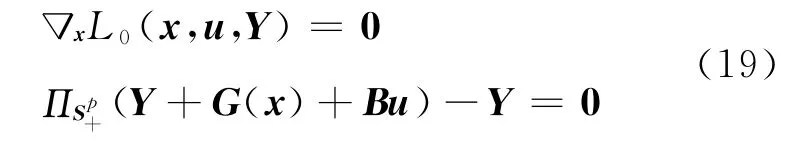
其中
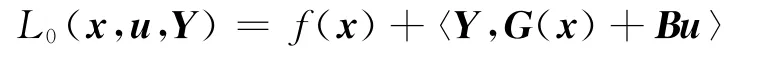
命题2 设f:Rn→R与G:Rn→Sp- 是二次连续可微函数和映射,对每一u∈Rm,(x(u),Y(u))处问题P(u)的雅可比唯一性条件成立.如果u*∈Uad是式(17)的局部极小点,则
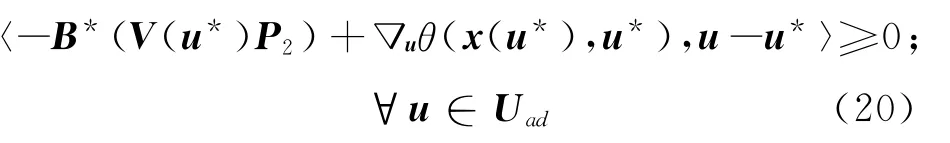
其中(P1,P2)∈Rn×Sp满足如下的伴随方程:
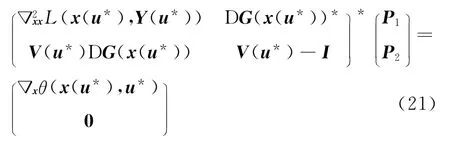
证明 定义θ0(u)=θ(x(u),u).如果u*∈Uad是式(17)的局部极小点,则
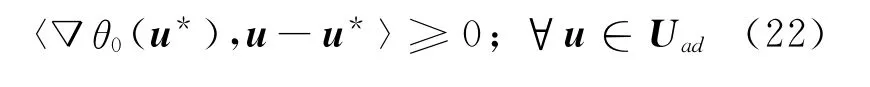
令

则
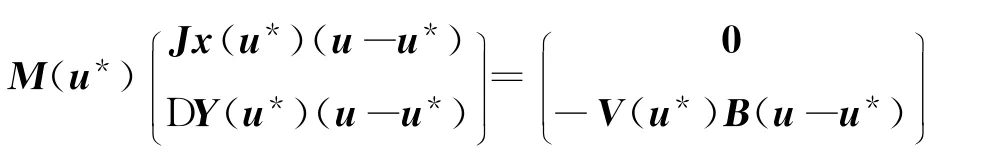
注意到式(21)可以表示为
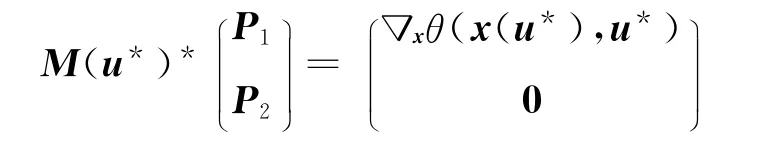
得到对u∈Uad,即式(20)成立.
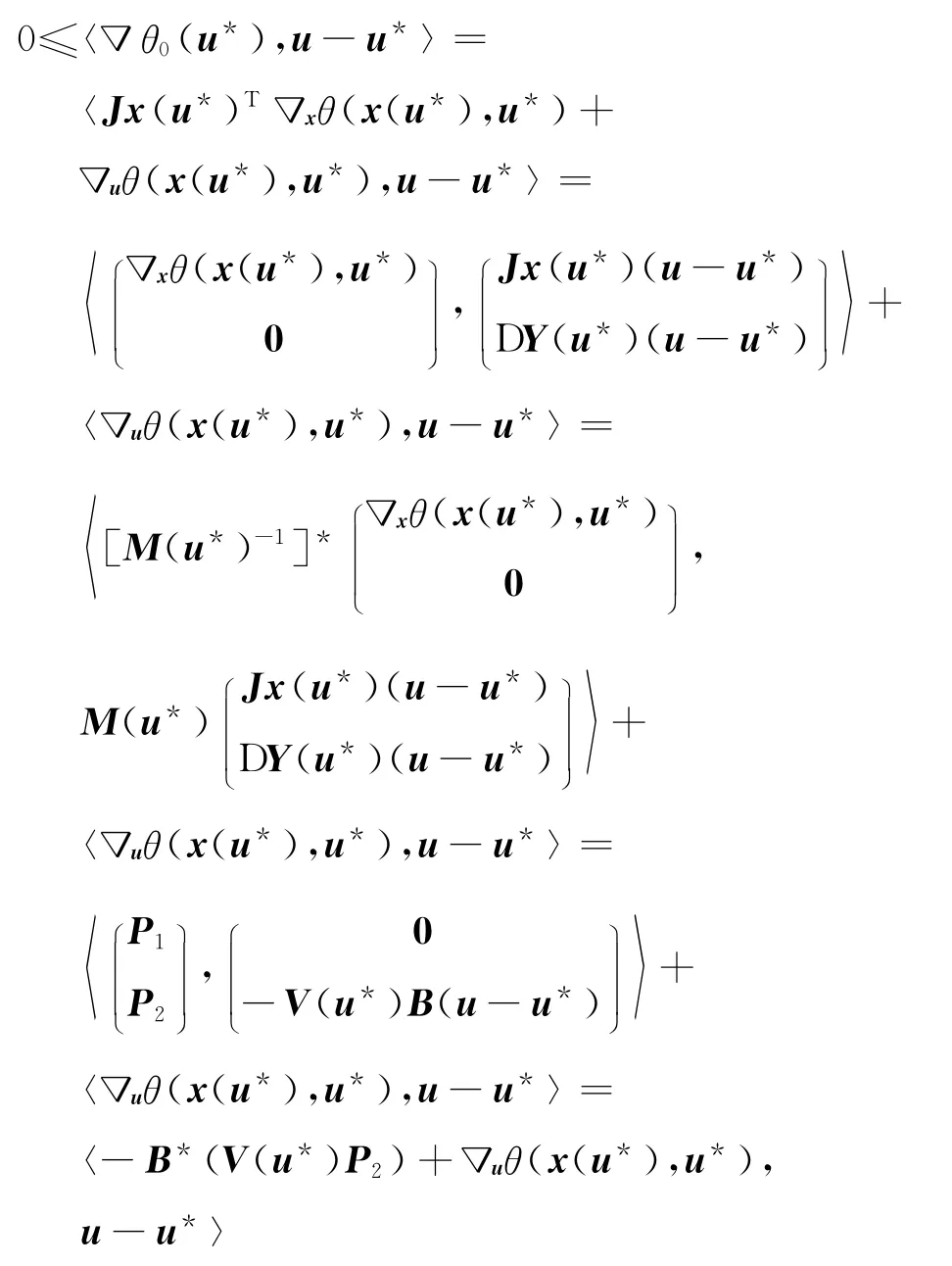
3 结 语
本文证明了非线性半定规划的雅可比唯一性定理,扰动问题的函数是决策变量与扰动参数的二次连续可微函数时的扰动解的连续可微性质,扰动函数的导数,以及一类下层为非线性半定规划的特殊双层规划的最优性条件.在雅可比唯一性条件中,严格互补条件是至关重要的,如果这一条件不成立,非线性半定规划的扰动性分析需要用到正半定矩阵锥的非光滑分析.非线性系统的强正则性和映射的Lipschtz同胚,与约束非退化条件和强二阶充分性最优条件等详见文献[7].
[1] Rockafellar R T,Wets R J B.Variational Analysis[M].Berlin:Springer,1998.
[2] Bonnans J F,Shapiro A.Perturbation Analysis of Optimization Problems [M].Berlin:Springer,2000.
[3] Klatte D,Kummer B.Nonsmooth Equations in Optimization:Regularity,Calculus,Methods and Applications [M].Boston:Kluwer Academic Publishers,2002.
[4] Facchinei F,Pang Jong-shi.Finite-Dimensional Variational Inequalities and Complementarity Problems:Volume I[M].Berlin:Springer,2003.
[5] Fiacco A V.Introduction to Sensitivity and Stability Analysis in Nonlinear Programming [M].New York:Academic Press,1983.
[6] Fiacco A V,McCormick G P.Nonlinear Programming:Sequential Unconstrained Minimization Techniques[M].Philadelphia:Society for Industrial and Applied Mathematics,1990.
[7] SUN De-feng.The strong second-order sufficient condition and constraint nondegeneracy in nonlinear semidefinite programming and their implications[J].Mathematics of Operations Research,2006,31(4):761-776.

