不完备软区分矩阵及其在决策问题中的应用＊

杨 勇，宋娟萍

（西北师范大学计算机科学与工程学院，甘肃 兰州730070）

1 引言

为解决现实中遇到的不确定问题，相继产生了一系列的数学理论和工具，比如粗糙集理论［1］、概率论、模糊集理论［2］等。但是，以上理论都存在其不完善的方面，主要不足之处是参数化工具的不完备。Molodstov D［3］于1999 年 提 出 了 软 集（Soft Set），成功解决了其它方法不能解决的参数化不足问题。软集参数的无约束性，使其解决不确定性问题的应用更广，也简化了决策过程。随后Maji P K 等学者［4］对软集理论作了进一步研究并给出了软集在决策问题中的应用［5］。近年来，软集的理论研究已经在很多领域取得了丰硕的成果［6～10］，与此同时，软集在许多实际问题尤其是决策问题中得到了广泛的应用［11～14］。在文献［15］中作者定义了软矩阵，提出了软矩阵算子以及解决决策问题的新方法。Feng Q 等［16］研究软集和信息系统之间的关系提出了软区分矩阵，并将其成功地用于决策问题，提出了全新的决策算法。

现实世界中会因数据测量的误差、对数据理解或获取的限制等因素，导致得到的信息系统往往是不完备的，基于此原因，本文结合不完备信息系统、软集以及区分矩阵，提出了不完备软区分矩阵，同时讨论其相关性质和运算。本文是对文献［16］的进一步学习和补充，部分地解决了不完备信息系统中的决策问题。最后，通过实例来验证新方法在解决决策不完备问题中的有效性。

2 预备知识

2.1 信息系统

定义1［17］（信息系统） 四元组（U，A，V，f）称为信息系统，或者是信息表。其中U为非空有限对象集合，称为论域；A为非空有限属性集合；V＝∪Vj，其中Vj表示属性aj的值域；f：U×A→V是一个信息函数，指明每个对象的属性值。

在一个信息系统中，若存在xi∈U，aj∈A，使得f（xi，aj）＝＊ ，这里的“＊”表示未知值，则称该系统为不完备信息系统。如表1所示的信息系统就是一个不完备信息系统。

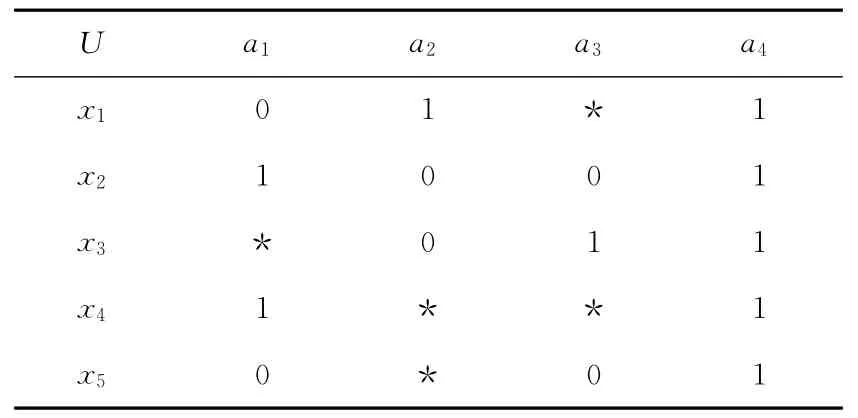
Table 1 An incomplete information systemS＝（U，A，V，f）表1 不完备信息系统S＝（U，A，V，f）

定义2［17］（划分） 设R是U上的等价关系，由不可区分关系R决定的U上的一个划分定义如下：A＝U｜R＝｛［xi］R：xi∈U｝，其中［xi］R＝｛xj：（xi，xj）∈R｝为包含元素xi的一个等价类。

2.2 软集

定义3［3］（软集） 设U为初始论域，E为参数集，P（U）为U上的幂集，A⊆E，F：A→P（U），称（F，A）为U上的软集。

换句话说，一个U上的软集就是U上的一些子集构成的参数族。对于任意的参数e∈A，F（e）可看作软集（F，A）的e－元素的集合或者是软集e－近似元素的集合。

定义4［18］（不完备软集） 设U为初始论域，E为参数集，A⊆E，F：A→ ｛0 ，1/2，1 ｝U，则称（F，A）为U上的不完备软集。

注：本定义中1/2 表示不完备软集中的未知值，即“＊”。

性质1［19］任何软集都是一个信息系统。

定义5［6］（软 二 元 关 系） 如 果F：A→P（U×U）是参数集A到幂集U×U上的映射，则U×U上的软集（F，A）称为U上的一个软二元关系。

定义6［11］（软等价关系） 设（F，A）是U上的软二元关系，如果对任意的e∈A，有F（e）≠∅且是U上的一个等价关系，则称（F，A）为U上的一个软等价关系。

定义7［11］（等价类） 设（F，A）是U上的一个软等价关系，则等价关系F（e）中包含元素x的等价类定义为：［x］F（e）＝｛y：（x，y）∈F（e），y∈U｝。

由上可知，软集（F，A）可确定一个不可区分关系，这个不可区分关系就是由参数决定的所有等价关系的交，即IND（F，A）＝∩ei∈AF（ei）。

设 （F，A）是U上 的 软 集，其 中U＝｛h1，h2，…，hm｝，则 由 不 可 区 分 关 系IND（F，A）决 定 的U上 的 划 分 为：U｜IND（F，A）＝｛c1，c2，…，ck｝（k≤m），其 中ci＝［hj］IND（F，A），hj∈U。

文献［11］提出了决策参数的概念，决策参数D＝∑hij中的hij为第i个对象hi关于第j个参数ej的值。在软集中条件参数和决策参数之间存在着很明确的关系，若使用粗糙集理论的属性约简方法可能会改变软集中最优对象的选择。因此，本文不对属性进行约简，通过建立区分矩阵来选择最优对象。为此介绍软集一致决策表的相关基本概念，这些概念和粗糙集的相关概念类似。

定义8［5］（软集的选择值） 设（F，A）是U上的软集，则对象hi∈U的选择值di＝∑jhij，其中hij为软集表中的元素。

决策参数值和每一个对象的选择值是相等的，下文中两者将不再区分。

定义9［16］（一致决策表） 设（F，A）是U上的软集，A⊆E，T＝（U，A＝C，D）是软集确定的决策表。当C⇒D，即IND（C）⊆IND（D），T称为软集的一致决策表，其中C是条件参数集，D是决策参数集。

定义10［11］（决策表中的不必要参数集） 设T＝（U，A，C，D）是一致决策表，Tγ＝（U，A，Cγ，Dγ）是在条件属性C中删除属性γ得到的决策表，其中Dγ表示删除γ后的决策参数集，且满足以下条件时称γ在T中是不必要的：

（1）Tγ是一致的，即C－γ⇒Dγ；

（2）IND（D）＝IND（Dγ）。

否则，称γ是决策表的必要参数或核参数。

由以上定义可知，在不完备软集中当且仅当C⇒D，即IND（C）⊆IND（D）时，决策表是一致的，所以我们可得到以下性质。

性质2U上的任何一个不完备软集都是一致的。

证明由粗糙集理论可知，对U上的一个等价关系R，有对任意的（xi，xj）∈R时，f（xi）＝f（xj）。由文献［11］可知，（F，A）为U上的软等价关系，在该关系中对任意的e∈A，F（e）是一个等价关系，因此，∩F（e）也是一个等价关系，它可以决定一个划分。在不完备软集（F，A）中决策参数D＝∑hij是由条件参数计算得到的，由条件参数决定的在同一个等价类中的对象必属于由决策参数决定的一个等价类中，所以IND（C）⊆IND（D），即C⇒D。因此，U上的任何一个不完备软集都是一致的。

性质3设（F，A）是U上的不完备软集，则IND（D）＝IND（Dγ）的必要条件是IND（Cγ）＝IND（C），其中Dγ表示从条件参数C中删除属性γ后的决策参数。

3 不完备软区分矩阵及其应用

区分矩阵最初是由Skowron A 和Rauszer C在文献［20］中提出的，主要用于属性约简。本文利用不完备软集确定的区分矩阵来解决决策问题。下面将介绍不完备软集上的区分矩阵，即不完备软区分矩阵。

3.1 不完备软区分矩阵

为了方便解决不完备信息系统下的决策问题，给出了以下定义。

定义11设U是论域，E是参数集，S＝（F，A）是U上的不完备软集，A⊆E，则F是U×A到V上 的 函 数，即F：U×A→V。因 此，F（hi，el）∈V，其中，hi∈U（i＝1，2，…，|U|），el∈A（l＝1，2，…，|A|），V＝ ｛0 ，1，1/2｝ 。当F（hi，el）未知时，F（hi，el）＝1/2。

定义12（基于对象的区分矩阵） 设S＝（F，A）是U上的不完备软集，A⊆E，称为（F，A）上 的 基 于 对 象 的区 分 矩 阵，其 中D（hi，hj）＝ ｛el∈A：F（hi，el）≠F（hj，el），hi，hj∈U｝为元素hi和hj的不完备软区分参数集，F（hi，el）和F（hj，el）是对象hi和hj关于参数el的值。

综上可知，在同一个划分类中的对象将位于同一个决策类中，即它们有相同的决策值。因此，我们可以通过定义不完备软集（F，A）上条件参数划分类的区分矩阵来缩小不完备软集（F，A）上区分矩阵的规模。

定义13（基于划分类的区分矩阵） 设S＝（F，A）是U上的不完备软集，A⊆E。S决定的划分 为U｜IND（F，A）＝｛Ci：i≤|U|｝。称为（F，A）上的基于划分类的区 分 矩 阵，其 中D（Ci，Cj）＝｛el∈A：F（hi，el）≠）F（hj，el），∀hi∈Ci，hj∈Cj｝为Ci和Cj的不完备软区分参数集，F（hi，el）和F（hj，el）是Ci中的对象hi和Cj中的对象hj关于参数el的值。

在下文中选用基于划分类的区分矩阵。接下来将给出例子来说明不完备软区分矩阵的相关概念。

例1［21］设U上的不完备软集（F，E）如表2所示，其中U＝｛h1，h2，h3，h4，h5，h6｝，条 件参数集E＝｛e1，e2，e3，e4，e5，e6，e7｝，最后一列增 加 了决策参数D＝∑hij，根据定义13来构造区分矩阵。

F（e1）的 等 价 类 为：｛h1，h4，h5｝，｛h2，h6｝，｛h3｝；

F（e2）的 等 价 类 为：｛h6｝，｛h1，h2，h4，h5｝，｛h3｝；

F（e3）的等 价 类 为：｛h1，h2，h6｝，｛h3｝，｛h4，h5｝；

F（e4）的等 价 类 为：｛h2｝，｛h3，h4，h5｝，｛h1，h6｝；

F（e5）的 等 价 类 为：｛h1｝，｛h3，h4，h5，h6｝，｛h2｝；

F（e6）的等 价 类 为：｛h2，h6｝，｛h4，h5｝，｛h1，h3｝；

F（e7）的等价类为：｛h2，h3｝，｛h1，h4，h5，h6｝。

Table 2 Incomplete soft set in example 1表2 例1中的不完备软集

Table 3 Discernibility matrix of Table 2表3 表2的区分矩阵

因为区分矩阵是对称的，所以我们只需表示出矩阵的一半元素，在本文中我们采用下三角的形式来表示区分矩阵。

软集经常被用来解决决策问题，从上面的定义中可知一个不完备软集就是一个不完备信息系统，而区分矩阵的定义形式也类似于信息系统，因此可以利用区分矩阵来解决不完备软集中的决策问题。

仅依据表3我们还是很难得到决策问题的答案。但是，由表3可知，决策值最大的对象将被选为最优对象，决策值的大小是由值为1和1/2的那些条件参数决定的，从而最优对象的条件参数的值为1和1/2的数量多于其它对象。由此可见，可以通过统计对象的参数值为1和1/2的那些参数的个数来确定最优对象。下面将给出不完备软区分矩阵的定义以及解决决策问题的算法。

定义14（不完备软区分矩阵） 设（F，A）是U上的不完备软集，A⊆E。（F，A）决定的划分U｜IND（F，A）＝｛Ci：i≤｜U｜｝。不完备软区分矩阵 定 义 为：其 中i，j≤U｝称为Ci与Cj的不完备软区分参数集，其中：

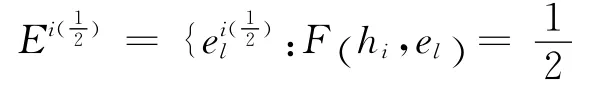
从以上定义我们可知Ei是在Ci中值为1且在Cj中值不为1的那些参数的集合，是在Ci中值为1/2且在Cj中值不为1/2的那些参数的集合；Ej是在Cj中值为1且在Ci中值不为1的那些参数的集合，是在Cj中值为1/2且在Ci中值不 为 1/2 的 那 些 参 数 的 集 合。 根 据 在D（Ci，Cj）中|Ei|、|Ej|、可以得到Ci和Cj的序关系。

根据定义14，通过再次分析Kong Z 在文献［21］中的例1，得到例1的软区分矩阵如表4所示。

根据例1，不可区分关系IND（F，E）将U划分为五类：C1＝｛h1｝；C2＝｛h2｝；C3＝｛h3｝；C4＝｛h4，h5｝；C5＝｛h6｝。

我们只给出D（C2，C1）的计算，其它不完备软区分矩阵参数的计算方式相同。在C1中只有一个对象h1，C2中只有一个对象h2。从表3中可知D（C2，C1）＝ ｛e1，e4，e5，e6，e7｝，从 表2 可 知F（h1，e1）＝1且F（h2，e1）＝0，F（h1，e5）＝1且F（h2，e5）＝1/2，因此F（h1，e4）＝1/2 且F（h2，e4）＝ 1，F（h1，e6）＝ 1/2 且F（h2，e6）＝1，所 以又F（h2，e4）＝1且F（h1，e4）＝1/2，F（h2，e5）＝1/2且F（h1，e5）＝1，F（h2，e6）＝1 且F（h1，e6）＝1/2，F（h2，e7）＝1且F（h1，e7）＝0，故所以，D（C2，C1）＝E1∪根据定义14得到的不完备软区分矩阵如表4所示。

注：对于C4，其中的对象h4和h5的决策值是相等的，因此可以选择其中的任意一个元素和其它类进行比较。

Table 4 Incomplete soft discernibility matrix of Table 2表4 表2的不完备软区分矩阵

性质4设（F，A）是U上的不完备软集，其中U＝｛h1，h2，…，hm｝，则（F，A）上的不完备软区分矩阵有如下性质：

（1）D（Ci，Ci）＝∅ （∀i≤m）；

（2）D（Ci，Cj）＝（Cj，Ci）（∀i，j≤m）。

性质5设（F，A）是U上的不完备软集，其中U＝｛h1，h2，…，hm｝。设d（Ci，Cj）＝｜D（Ci，Cj）｜，其 中D（Ci，Cj）表 示 集 合D（Ci，Cj）的基数。则d（Ci，Cj）有如下性质：

（1）d（Ci，Ci）＝0（ ∀i≤m）；

（2）d（Ci，Cj）＝d（Cj，Ci）（∀i，j≤m）。

由 定 义14 和 性 质5 可 知：d（Ci，Cj）＝当时，为了更好地解决决策问题，令因此，在做决策时只需要计算和便可得到Ci和Cj的序关系，因此得到如下性质：

性质6在不完备软区分矩阵中，如果表示Ci与Cj在相同的决策类中；如果，则表示Ci与Cj之间有一个序关系，即Ci优于Cj或Cj优于Ci。

性质7在不完备软区分矩阵中，如果则有以下两种情况：

3.2 基于不完备软区分矩阵的决策算法

算法基于不完备软区分矩阵的决策

输入：U上的不完备软集S＝（F，A），其中U＝｛h1，h2，…，hm｝。

输出：所有对象的序关系。

步骤1计算U的划分以及不完备软区分矩阵＝（D（Ci，Cj） ）i.j≤U。

步骤3根据性质7给出Ci和Cj的序关系。

步骤4根据步骤3输出所有对象的序关系。

接下来将继续使用例1来阐述上文给出的算法。

例2不完备软集如表2所示，利用算法1给出所有对象的序关系。

步骤1从表2 我们得到U的划分为：｛｛h1｝，｛h2｝，｛h3｝，｛h4，h5｝，｛h6｝｝，这 五 个 类 分别标记如下：C1＝｛h1｝；C2＝｛h2｝，C3＝｛h3｝，C4＝｛h4，h5｝和C5＝｛h6｝。不完备软区分矩阵如表4所示。

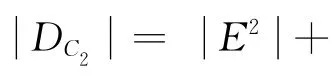
同理，

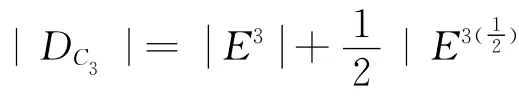
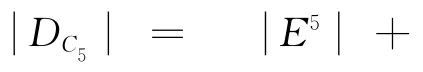
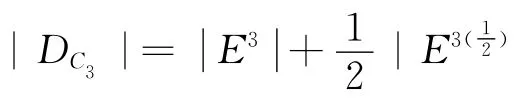
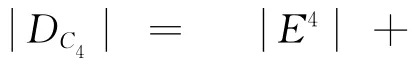
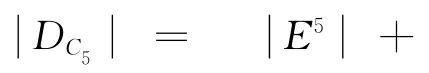
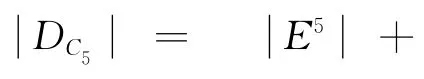
步骤3根据性质7 以及步骤2 步可得：有知C2优于C1，即h2＞h1。同理：C1优于C6，即h1＞h6；C3优于C4，即h3＞｛h4，h5｝；C5优于C3，即h6＞h3。其它一样，这里将不再一一列出。

步骤4根据步骤3 得到对象的序关系为：h2＞h1＞h6＞h3＞｛h4，h5｝。因此，最优对象为h2。

实际应用中，有时候我们不仅需要得到最优对象而且需要次优对象，该方法可以获得所有对象的序关系，在实际中将会有更广泛的应用价值。且该方法使用区分矩阵来解决不完备信息的决策问题，后期可以使用该方法来研究不完备信息系统下的属性约等问题。接下来通过另一个例子来说明该方法的有效性。

例3设（F，E）是U上的不完备软集，其中U＝{h1，h2，h3，h4，h5，h6，h7，h8}，条件参数集E＝｛e1，e2，e3，e4，e5，e6，e7，e8，e9，e10，e11，e12，e13，e14，e15｝，不完备软集F，（E） 如表5所示。利用算法1给出所有对象的序关系。

观察表5发现，e3、e13和e15的值全是0和1，所以这三个参数不会出现在任何集合的区分矩阵中，因此删除这三个参数对最后的决策没有任何影响，即这三个参数是不必要的，并且在建立的不完备软区分矩阵表6中也没有出现。故该方法不仅可以用于解决决策问题，还可以用于属性约简，这将在后期加以研究。

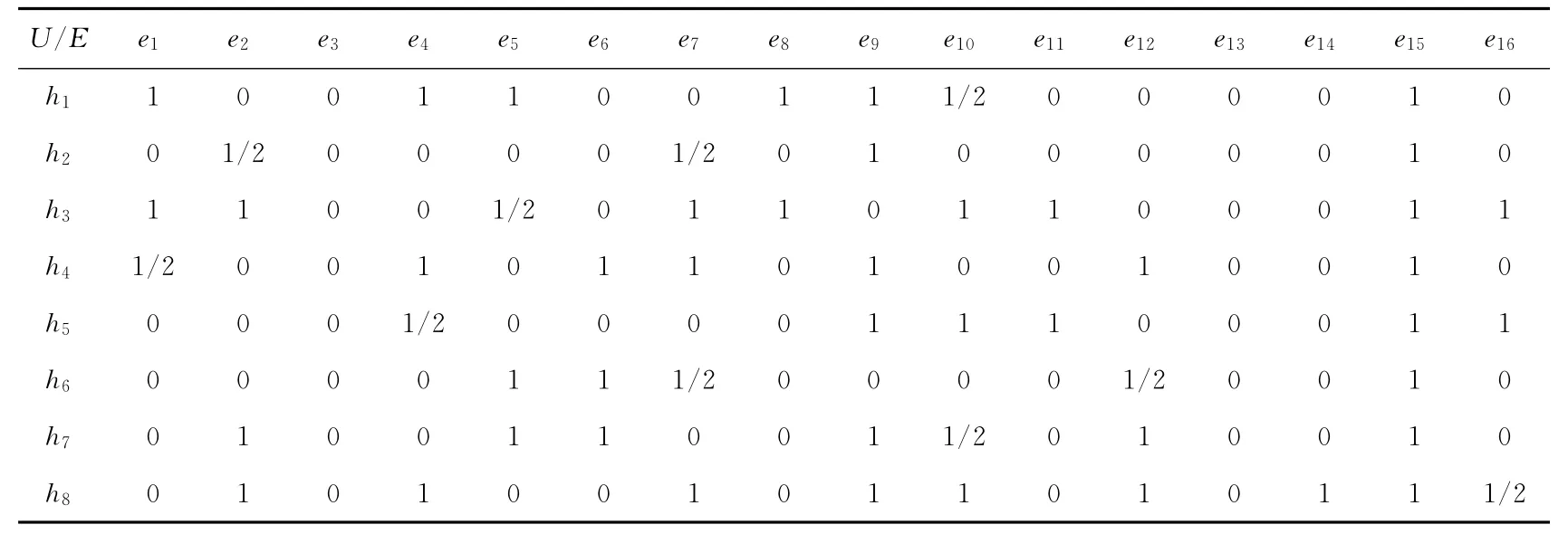
Table 5 Incomplete soft set in example 3表5 例3的不完备软集

Table 6 Incomplete soft discernibility matrix of example 3表6 例3的不完备软区分矩阵

4 结束语

基于已提出的软区分矩阵在决策问题中的应用，本文首先提出了不完备软区分矩阵概念及其相关性质，并给出了不完备软区分矩阵的决策算法。最后通过实例表明，该算法仅需一次扫描不完备软区分矩阵，便可得到所有对象的序关系，不仅可选择出最优对象也可得到次优对象。在此基础上，今后我们将通过实践，进一步研究不完备软集在决策问题中的应用以及将不完备软区分矩阵用于属性约简。

［1］ Pawlak Z.Rough sets［J］.International Journal of Computer＆Information Sciences，1982，11（5）：341－356.

［2］ Zadeh L A.Fuzzy sets［J］.Information and Control，1965，8（3）：338－353.

［3］ Molodtsov D.Soft set theory－first results［J］.Computers ＆Mathematics with Applications，1999，37（4）：19－31.

［4］ Maji P K，Biswas R，Roy A R.Soft set theory［J］.Computers＆ Mathematics with Applications，2003，45（4）：555－562.

［5］ Maji P K，Roy A R，Biswas R.An application of soft sets in a decision making problem［J］.Computers ＆ Mathematics with Applications，2002，44（8）：1077－1083.

［6］ Ali M I.A note on soft sets，rough sets and fuzzy soft sets［J］.Applied Soft Computing，2011，11（4）：3329－3332.

［7］ Ali M I，Feng F，Liu X Y，et al.On some new operations in soft set theory［J］.Computers ＆ Mathematics with Applications，2009，57（9）：1547－1553.

［8］ Babitha K V，Sunil J J.Soft set relations and functions［J］.Computers ＆ Mathematics with Applications，2010，60（7）：1840－1849.

［9］ Molodtsov D.The theory of soft sets［M］.Moscow：URSS Publishers，2004.

［10］ Pei D，Miao D.From soft sets to information systems［C］∥Proc of GrC，2005：617－621.

［11］ Ali M I.Another view on reduction of parameters in soft sets［J］.Applied Soft Computing，2012，12（6）：1814－1821.

［12］ Çagman N，Enginoglu S.Soft set theory and uni－int decision making［J］.European Journal of Operational Research，2010，207（2）：848－855.

［13］ Chen D，Tsang E C C，Yeung D S，et al.The parameterization reduction of soft sets and its applications［J］.Computers ＆ Mathematics with Applications，2005，49（5）：757－763.

［14］ Geng Sheng－ling，Li Yong－ming，Liu Zhen.Incomplete soft sets and dominance credible reles mining［J］.Computer Engineering ＆Scinece，2013，35（12）：153－160.（in Chinese）

［15］ Çagman N，Enginoglu S.Soft matrix theory and its decision making［J］.Computers ＆ Mathematics with Applications，2010，59（10）：3308－3314.

［16］ Feng Q，Zhou Y.Soft discernibility matrix and its applications in decision making［J］.Applied Soft Computing，2014，24：749－756.

［17］ Pawlak Z.Information systems theoretical foundations［J］.Information Systems，1981，6（3）：205－218.

［18］ Han B H，Li Y M，Liu J，et al.Elicitation criterions for restricted intersection of two incomplete soft sets［J］.Knowledge－Based Systems，2014，59：121－131.

［19］ Zou Y，Xiao Z.Data analysis approaches of soft sets under incomplete information［J］.Knowledge－Based Systems，2008，21（8）：941－945.

［20］ Skowron A，Rauszer C.The discernibility matrices and functions in information systems［M］∥Intelligent Decision Support，Netherlands：Springer Netherlands，1992：331－362.

［21］ Kong Z，Gao L，Wang L，et al.The normal parameter reduction of soft sets and its algorithm［J］.Computers ＆ Mathematics with Applications，2008，56（12）：3029－3037.

附中文参考文献：

［14］ 耿生玲，李永明，刘震.不完备决策软集与优势可信规则获取［J］.计算机工程与科学，2013，35（12）：153－160.