基于满二叉树的二分K－means聚类并行推荐算法＊

陈平华，陈传瑜

（广东工业大学计算机学院，广东 广州510006）

1 引言

随着网络应用的飞速发展，网络数据呈现指数增长，出现了“信息过载”问题，推荐系统应运而生［1］。协同过滤作为应用最广泛的推荐算法，其简单的模型理念和实现备受大型企业青睐［2］。然而，随着用户数和物品数的指数上升，计算量急增，协同过滤算法遇到了性能瓶颈。于是，通过聚类算法减少协同过滤中寻找最相似邻居集的匹配次数同时又不降低推荐准确性成为当前推荐领域热点。

为了减少最相似邻居集的匹配次数同时不降低推荐准确性，文献［3］采用中心聚类算法，先求出各样本与其所属类别之间的类别关联度，再利用类别关联度区别对待预测样本的最近邻；文献［4］利用聚类算法使数据平滑，以组合传统协同过滤和聚类形成推荐算法；文献［5］利用蚁群聚类算法，并结合协同过滤算法挖掘用户的隐含模式，从而将相似用户进行较为准确的分类；文献［6］将PCA 和聚类算法组合协同过滤，形成推荐，减少目标用户的最近邻搜索范围；文献［7］组合两种聚类算法：Kmeans和SOM，以此提高推荐系统的准确性；文献［8］利用遗传算法将聚类和协同过滤组合起来进行项目推荐；文献［9］将用户聚类和项目聚类进行交叉迭代，使得聚类簇达到较为稳定的状态。

不过，传统聚类算法，如K－means、DBSCAN等，应用于推荐系统时存在如下不足：将用户归入最相似目标簇后，推荐过程只针对目标簇成员，与其他簇成员无关，可能造成与用户相似的其他簇内成员丢失，降低推荐系统的准确性。此处，传统聚类算法（非模糊聚类）不能使聚类对象同时属于多个类别，比如一篇属于体育又属于娱乐的新闻报道，K－means可能将其归入到体育类别中，也可能归到娱乐类别中，但不能同时归为这两个类别。为了解决这些问题，本文提出一种基于满二叉树的K－means聚类并行推荐算法K－FBT（BisectingKmeans clustering parallel recommendation algorithm based on Full Binary Tree）。K－FBT 算 法中K值代表的不再是簇的个数，而是满二叉树的深度，同时也代表用户最多可属于簇的个数。由于聚类后的K个簇并无关联，所以基于K－FBT 算法的推荐过程可并行执行，可应用MapReduce等分布式系统框架。

2 满二叉树

二叉树是一种应用广泛的非线性数据结构，特点是每个节点至多有两棵子树（即二叉树不存在度大于2的节点）［10］。二叉树中有三类节点：树根节点、非叶子节点、叶子节点。满二叉树是二叉树的一种特殊情形。满二叉树具有以下性质：

定义1总节点数是2k－1，第i层的节点数是2i－1（k代表树的深度）。

定义2除最后一层无任何子节点外，其它层上每个节点均有两个子节点。

定义3从上往下编号（从1开始），第i个节点的左孩子编号是2＊i，右孩子是2＊i＋1。

定义4从上往下编号（从1开始），第i个节点的父亲编号是i/2（保留到整数位）。

3 K－means与满二叉树

3.1 K－means

MacQueen J提 出 了K－means聚 类 算 法［11］。K－means的主要优点是：算法可快速收敛，并得到局部的最优解。K－means算法应用于推荐系统时的主要思想是：给定n个数据点（向量）｛X1，X2，…，Xn｝，找到K个聚类中心｛A1，A2，…，AK｝，使得每个数据点（向量）与其最近的聚类中心的相似度和最大，并以这个相似度和为目标函数，记作W。设Sim（Xi，Aj）表示数据点Xi和簇中心Aj的相似度，计算如公式（1）所示：

3.2 K－FBT算法

K－FBT 算法的基本思想是初始数据集作为树根节点，再通过二分K－means算法将数据集分成两簇，并使这两个簇成为其左右孩子节点。接着，对这两个节点进行同样的操作，直到形成一棵满二叉树且深度为K，算法结束。其中，树根节点存储初始数据集，非叶子节点存储簇的中心向量，叶子节点存储簇的中心向量和簇内数据集。实现如算法1所示：

算法1创建满二叉树算法

输入：初始数据集Dataset，二叉树深度K。

输出：满二叉树。

步骤1初始数据集设定为树根节点；

步骤2初始化队列，树根节点入队；

步骤3根据定义1，计算K层节点总数；

步骤4队头元素出队，执行二分K－means算法；

步骤5将步骤4所得，作为步骤4元素的左右孩子并入队；

步骤6步骤3节点总数减1，若节点总数大于0则执行步骤4，否则算法结束。

3.3 簇内凝聚度

通过算法1可得到满二叉树。但是，分裂过程中可能存在一种情况：簇内已经有很高的凝聚度，不再需要分裂。基于此，本文引入簇内凝聚度CCL（Cluster Cohesion Level），认为CCL达到一个阈值α后，就无需继续分裂。以Sim（Ui，Centerj）表示第i个用户和第j个簇之间的相似度，Centerj表示第j个簇的中心向量，Clusterj表示第j个簇内的用户集，Count（Clusterj）表示第j个簇内用户集的个数。CCL是簇内所有用户集与该簇中心向量相似度之和的均值，计算如公式（2）所示：

采用CCL作为分裂阈值后，由于有节点不会继续分裂，因此可能无法构成一颗满二叉树。针对这种情况，本文采取填补空节点的方法使其建立一棵伪满二叉树。故本文的满二叉树存在四类节点：树根节点（用＃表示）、非叶子节点（用＋表示）、叶子节点（用－表示）、空节点（用N 表示）。空节点仅仅起到占位符的作用，本身并不携带任何信息，其作用是方便对多个簇的预测结果进行合并时，计算每个簇对应的权值。伪满二叉树如图1所示，线上数值表示CCL。

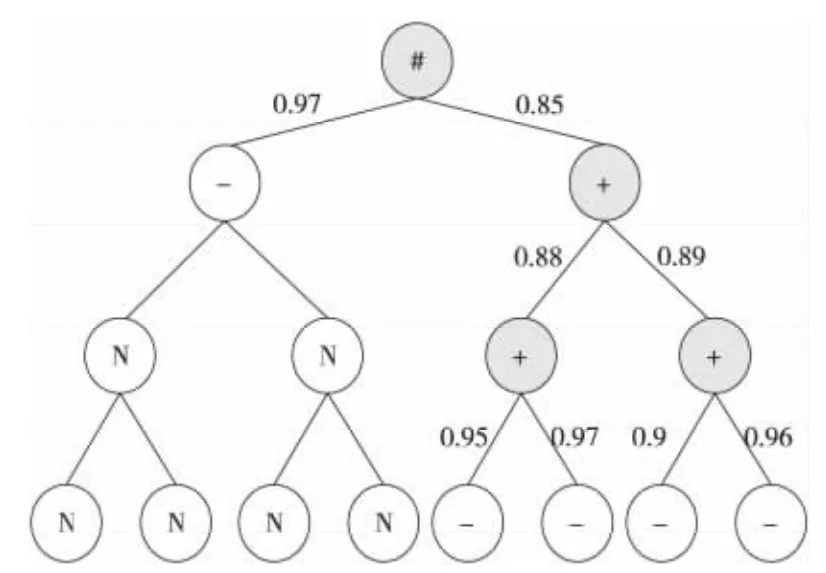
Figure 1 A full binary tree by filling blank nodes图1 填补空节点的满二叉树

4 推荐过程

4.1 层次遍历

根据目标用户的历史行为记录，建立对应的向量空间模型VSM （Vector Space Model）。接着针对目标用户，进行层次遍历算法。其算法主要思想是：从满二叉树的第二层开始迭代寻找属于用户的K个最佳叶子节点（簇）。在K－FBT 算法中，用户可以归入到当前层的节点数目（簇）等于这一层的深度。比如用户和第三层的四个节点（定义1）进行相似度比较，用户可以归入到相似度靠前的三个节点中。然后，用户再向下遍历这三个节点的子节点，总共是六个节点（定义2）。由于此时是处于第四层，用户可以归入到相似度靠前的四个节点中。最后，直到节点为叶子节点，遍历结束。算法结束后，用户将从属于K个叶子节点（簇）。

由于分裂阈值的原因，用户从属的K个叶子节点（簇）可能不会处于满二叉树的同一层次，所以需要对上述层次遍历算法进行修正。实现过程见算法2：

算法2目标用户相似簇发现算法

输入：满二叉树BT，目标用户特征向量ActiveUse－rVector。

输出：K个叶子节点（簇）。

步骤1初始化四个队列，BT树根节点加入队列1；

步骤2队列1元素依次出队，并将该层元素入队到队列2；

步骤3计算目标用户和队列2中所有元素节点的相似度，将相似度值和节点编号加入到队列3；

步骤4归一化队列3的相似度值，接着，根据相似度降序排列，（当前深度－队列4元素个数）之后的队列元素出队；

步骤5队列3元素依次出队，若元素为叶子节点，则加入到队列4，否则元素加入到队列1；

步骤6若队列4元素个数小于K且队列1非空，执行步骤2，否则算法结束并返回队列4。

通过设定适当的分裂阈值，能够有效地减少创建二叉树时执行K－means算法的次数，显著地缩短预处理时所需的时间。另外，对于规则" 用户可以归入当前层的节点数目等于这一层的深度”也需作出相应修改，变更为“用户可以归入当前层的节点数目等于这一层的深度减去已选择的叶子节点数目”，如图2所示，线上数值表示目标用户与簇中心的相似度，右边等式表示目标用户处于该层时可归入节点（簇）数。

Figure 2 Selecting the optimal Kclusters图2 选择最优的K 个簇

4.2 分布式预测

Figure 3 Executing process of the MapReduce图3 MapReduce的执行过程

根据上一节得到的K个叶子节点（簇），分别找出和用户最相似的邻居集。最后，根据这K个邻居集分别对用户未评分项目进行预测。由于K个叶子节点（簇）之间并无任何关联，所以可以通过并行化的手段来提高推荐系统的性能，同时增强系统的可扩展性。对于大数据的处理或者聚类，应用MapReduce框架可以较快地完成［12］。所以，本文在Hadoop平台上利用MapReduce并行处理框架对这K个不同的簇进行分布式处理。由于需要计算用户相似度和预测评分两个步骤，所以需要两个MapReduce顺序组合起来执行，处理步骤如下：

Mapper1：首先读取HDFS中数据信息，以行读取，每行数据由树节点ID、用户信息（包括用户ID、用户特征向量）组成。接着使用相似度度量方法（如余弦相似度、Pearson相关系数、修正余弦相似度等方法），计算该用户和目标用户的相似度。最后，输出新的键值对〈树节点ID－相似度，用户ID〉，其中，该输出键值对中key为复合键，主要是为了实现树节点ID 升序且相似度降序排列。

Partitioner1：为了实现按照树节点ID 升序排列，并且若树节点ID 相同，则按照相似度降序排列的需求，需要重写 WritableComparator 类和GroupComparator类。另外，由于Reducer的输入参数中key是需要根据树节点ID 来划分，所以在Partitioner类中需要重写getPartition方法，使分片时按照树节点ID 划分。

Reducer1：输入键值对〈树节点ID－相似度，用户ID〉。将输入键值对作简单变换，形成新的键值对〈树节点ID，用户ID－相似度〉。由于数据已按照相似度降序排列，所以只选取前N个输入键值对作为输出键值对。

Mapper2：输入键值对〈树节点ID，用户ID－相似度〉。根据用户ID 获取用户的历史评分记录，形成新的键值对〈树节点ID－项目ID，相似度－用户评分均值－该项目评分值〉。

Reducer2：输入键值对〈树节点ID－项目ID，相似度－用户评分均值－该项目评分值〉，根据预测公式对每个树节点中的项目进行评分预测。最后，形成新的键值对〈项目ID，树节点ID－参与人数－预测分数〉，保留树节点ID 和参与人数是为了对相同项目合并时权值的计算。

根据上述步骤，可以完成多个树节点（簇）对目标用户未评价项目的评分预测，然后将评分高的项目推荐给目标用户。但是，不同树节点的推荐结果中可能存在相同的项目，所以需要将这些相同项目进行评分合并。

4.3 合并策略

4.3.1 节点权值

由于K个叶子节点（簇）的聚合程度不相同，并且所在层次也不相同，所以得到的权值也应不相同。有以下三种情况：

（1）层次越低的叶子节点（簇）内成员会越少，即层次越低的叶子节点（簇）的聚合程度应该更高，对应的权值应更高。

（2）有共同祖先节点的叶子节点，自身与目标用户相似度越高，对应的权值就应越高。

（3）同一层且无相同父节点的叶子节点可能具有不同的祖先节点。换句话说，祖先集与目标用户相似度越高，对应子孙节点的权值就应该越高。

为了满足上述三点，本文提出一种节点权值计算方法，记作NodeWeighti，k。根据定义4，满二叉树中任意节点的所有祖先都可以被获得，记作NodeSet。NormalSim（i，j）表示目标用户i和归一化后第j个簇的相似度值。NodeSet包括自身。计算如公式（3）所示：

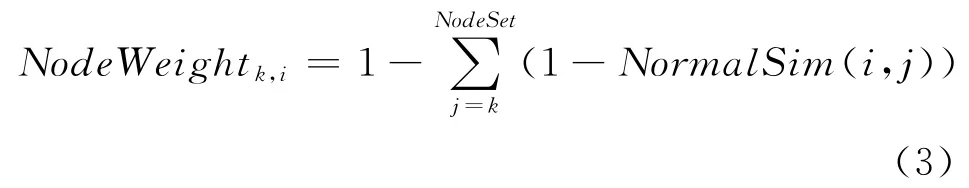
图4中线上数值是对图2中相似度进行归一化后的结果。图5中线上数值表示该节点（簇）的权值。从图4和图5可以看出，层次越低的叶子节点（簇）得到的权值越高；同一层次且相同祖先的节点的权值由自身权值所决定，是正相关关系。同一层次且不同祖先的节点的权值由祖先节点的权值和自身权值所决定，并且两者是正相关关系。经实验表明，这种节点权值的计算方法能够有效地提高推荐系统的准确性。

Figure 4 A full binary tree after normalizing similarities图4 归一化后的满二叉树

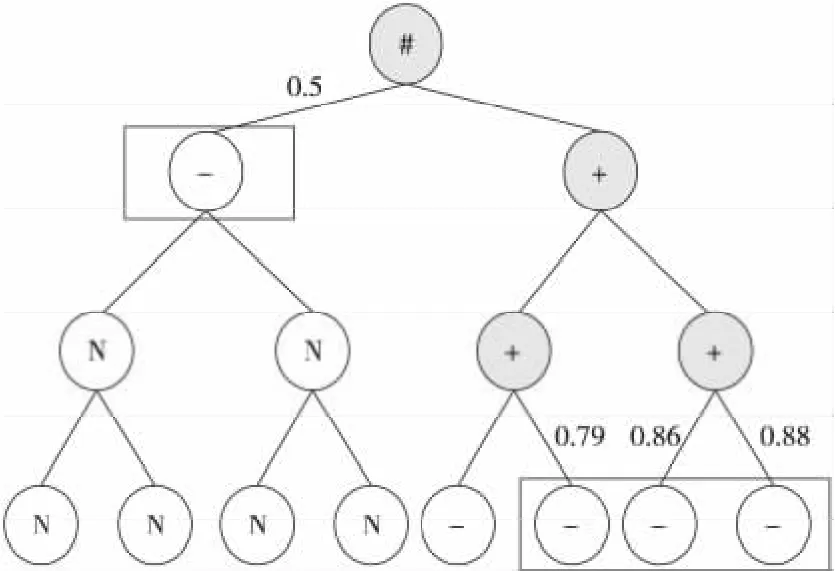
Figure 5 A full binary tree of node weights图5 节点权值的满二叉树

4.3.2 人数权值

每个簇内参与预测相同项目的人数越多，则这个簇对该项目的评分预测会更加准确。所以，本文认为簇内对相同项目的预测人数应作为合并权值的一部分，记作CountWeight。

4.3.3 最终评分

本文结合上述两种策略对公共项目进行评分合并。给定：PUi，Ij表示预测用户i对项目j的评分，NodeWeight（k，Ui）表示用户i对于第k个簇的节点权值，CountWeight（k，Ij）表示第k个簇内参与预测项目j的人数权值，Predict（k，Ui，Ij）表示第k个簇预测用户i对项目j的评分。计算如公式（4）所示：

5 实验分析

5.1 实验环境

K－FBT 算法的仿真实验在具有五个节点的计算机集群上实现。集群的单个节点采用联想ThinkCentre M8400t普通商用台式机，电脑具体配置：CPU 是Intel酷睿i7 4770S，内存大小是4GB，硬盘大小是1 TB。操作系统采用Linux ubuntu12.10。所有的节点由一个千兆以太网交换机相连，其中一个节点配置成NameNode 与Job Tracker，其余的四个节点配置为DataNode，MapReduce平台采用分布式开源平台Hadoop1.2.1。

5.2 实验数据集

实验采用目前衡量推荐系统质量广泛使用的MovieLens数据集，该数据集来自美国明尼苏达大学研究小组GroupLens。它包含了943 名用户对1 682部电影的评分，每个用户至少已经评分20 部电影，评分集为｛1，2，3，4，5｝，共100 000条评分记录。评分越大说明用户对所评电影的认可度越高。实验中将数据集分为10等份，使用留一法交互验证进行实验分析。

5.3 评估标准

针对推荐系统性能评估的方法有很多，如平均绝对误差、召回率、准确率、均方根误差、多样性和新颖性等，本文采用推荐所用时间UTIR（Used Time In Recommended）和 平 均 绝 对 误 差MAE（Mean Absolute Error）来衡量推荐系统的性能好坏。UTIR表示推荐系统对一个用户产生推荐结果的时间。UTIR主要用来测量推荐效率，UTIR越小，说明推荐效率越高。MAE主要是计算系统预测推荐值与用户真正评价值之间的差异程度，MAE值越小，系统的推荐质量就越高。MAE的定义如公式（5）：

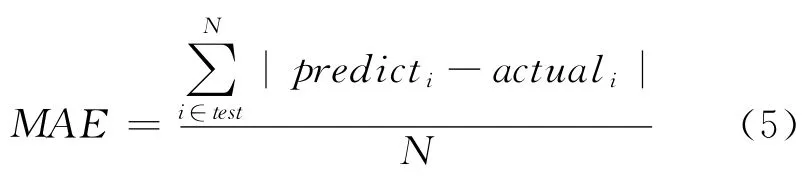
5.4 实验内容

实验1为了验证K－FBT 算法对初始中心的依赖性，设计如下实验：初始中心在训练集中随机选择，并分别执行K－FBT 算法和传统K－means聚类推荐算法（K－means算法）。接着，根据推荐结果和实际结果的差异，计算MAE。反复进行该实验10次，计算MAE均值和MAE标准差，实验结果如表1和表2所示。

Table 1 Experimental results of K－FBT表1 K－FBT算法的实验结果数据

Table 2 Experimental results of K－means表2 K－means算法的实验结果数据

实验2当CCL达到一个值后，分裂就应该被停止。为了观察CCL对于推荐结果的影响，设计如下实验：给定邻居数目为20，K＝5 的条件下，通过调整分裂阈值，观察MAE值的变化，实验结果如图6所示。

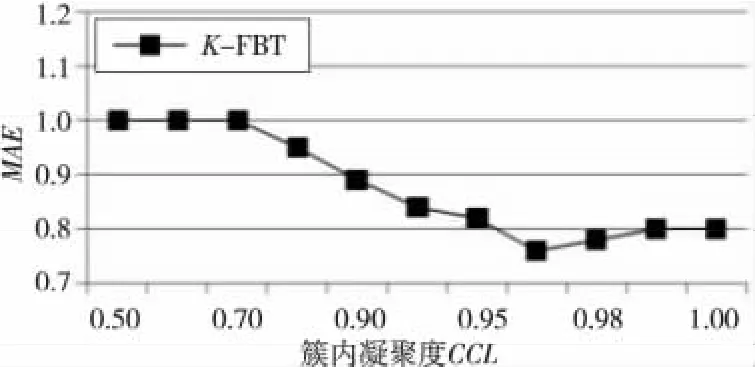
Figure 6 MAEof the K－FBT algorithm（different CCL）图6 K－FBT 算法的MAE（不同CCL）

实验3为了验证本文所提出的K－FBT 算法的性能，设计如下实验：将传统的基于用户的Kmeans的协同过滤算法（User－Based Cluster）、基于项目 聚 类 的 协 同 过 滤 算 法（Item－Based Cluster）、基于遗传算法的聚类推荐算法（Genetic Cluster）［8］和K－FBT 算法进行比对。在测试数据集上，这四种算法在不同K的取值上的性能表现如图7所示。

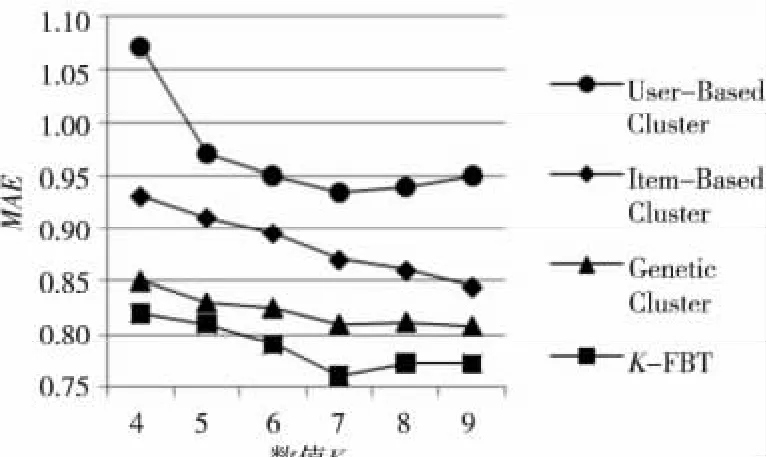
Figure 7 MAEof the four algorithms（different Kvalue）图7 四种算法的MAE 比较（不同K 值）

实验4为了验证用户邻居数的选定对于推荐结果的影响，设计如下实验：给定K＝7，CCL＝0.976的条件下，将传统的基于COS的协同过滤算 法（COS CF）、迭 代 聚 类 调 整 算 法（Iterative CF）［9］和K－FBT 算法进行比对。在测试 数据集上，这三种方法在不同近邻个数上的性能表现如图8所示。

Figure 8 MAEof the three algorithms（different neighbor numbers）图8 三种算法的MAE 比较（不同邻居数）

实验5为了验证K－FBT算法的高效性，设计如下实验：给定K＝7，CCL＝0.976的条件下，将KFBT算法与传统基于K－means的协同过滤算法（Kmeans Cluster）进行实验比较，通过测量UTIR进行实验结果对比。实验结果如图9所示。

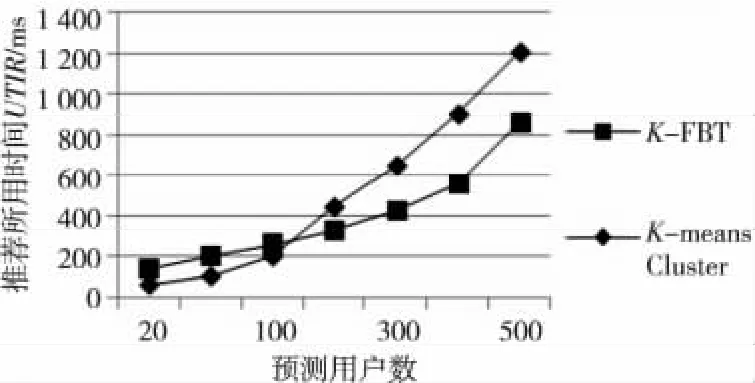
Figure 9 UTIR of the K－FBT and the K－means Cluster（different predicting user numbers）图9 K－FBT 和K－means Cluster的UTIR 比较（不同的预测用户数）

5.5 实验分析

从表1 和表2 可发现，本文K－FBT 算法的MAE均值和MAE标准差均比K－means算法要小，即K－FBT 算法对初始中心的依赖远远小于传统的K－means聚类推荐算法。所以，K－FBT 算法可以有效地降低初始中心对于推荐结果的影响，并且可以提高推荐结果的准确性。

从图6可发现，当CCL≤0.7时，MAE的结果都相同。这是因为当第一次分裂后的两簇的CCL都会大于0.7。则当CCL≤0.7时，K－FBT 算法创建的都是深度为2的满二叉树（3个节点）。当CCL＞0.99时，MAE的结果亦都是相同的。这是因为在分裂过程中生成的树节点的凝聚度都小于0.99。当CCL＞0.99时，K－FBT 算法创建的都是深度为K的真满二叉树。当CCL＝0.976时，KFBT 算法将取得最佳的性能。

由图7 和 图8 可 发 现，K－FBT 算 法 的MAE比其他算法的小，即本文算法的准确性比其他算法要高。可以看出，满二叉树与K－means聚类算法的结合可以提高推荐的准确性，可较为有效地解决聚类算法的不足。当用户邻居数为25，K＝7，CCL＝0.976 时，K－FBT 算法表现出最好的推荐效果。

由图9可发现，K－FBT 算法平均对每个用户进行推荐的所用时间要少于K－means算法所需的时间。这就证明了K－FBT 算法利用MapReduce并行处理框架，可显著地缩短对用户进行推荐所用的时间。从实验中可发现，当预测用户数小于100时，K－FBT 算法的推荐所用时间多于K－means算法，这是因为MapReduce框架并行处理需要一定的额外开销，比如数据的分割、数据的汇总等。这就造成了当预测用户数量较小时，额外开销占据了系统总用时的绝大部分。但是，当预测用户数量较大时，这部分开销是可以被忽略的。另外，实验中也可发现，预测用户数从400～500的直线斜率要比300～400的直线斜率要陡，这是因为实验环境只配备了五台物理电脑。当预测用户数大概等于350时，系统性能达到最好。实验表明，如果额外增加物理电脑，可以提高系统性能，即提高系统的可扩展性。

6 结束语

针对聚类算法存在的不足，本文结合树结构和K－means聚类算法，将所有用户聚类到一棵满二叉树中。在执行过程中，采用簇内凝聚度控制分裂，最后创建一棵满二叉树。实验表明：本文算法对于聚类的初始中心依赖要远远低于其他的Kmeans聚类推荐算法。因此，本文算法不仅有效解决了传统聚类算法的不足，而且适用于分布式框架，可显著提高算法执行效率和增强可扩展性。本文算法中，CCL的设定需要经验或者通过迭代寻找最优值，这是本文算法在通用性方面的局限性。接下来，我们将考虑如何改进CCL阈值的设定，使其能自适应不同的复杂推荐系统。

［1］ Resnick P，Varian H R.Recommender systems［J］.Communications of the ACM，1997，40（3）：56－58.

［2］ Breese J S，Heckerman D，Kadie C.Empirical analysis of predictive algorithms for collaborative filtering［C］∥Proc of the 14th Conference on Uncertainty in Artificial Intelligence，1998：43－52.

［3］ Yin Hang，Chang Gui－ran，Wang Xing－wei.Effect of clustering algorithm inK－nearest－neighborhood based collaborative filtering［J］.Journal of Chinese Computer Systems，2013，34（4）：806－809.（in Chinese）

［4］ Xue G R，Lin C，Yang Q，et al.Scalable collaborative filtering using cluster－based smoothing［C］∥Proc of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval，2005：114－121.

［5］ Cao Bo，Su Yi－dan.Web log mining based on ant clustering［J］.Microcomputer Information，2009（9）：225－226.（in Chinese）

［6］ Yu Xue，Li Min－qiang.Collaborative filtering recommendation model based on effective dimension reduction andKmeans clustering［J］.Application Research of Computers，2009，26（10）：3718－3720.（in Chinese）

［7］ Tsai C F，Hung C.Cluster ensembles in collaborative filtering recommendation［J］.Applied Soft Computing，2012，12（4）：1417－1425.

［8］ Feng Zhi－ming，Su Yi－dan，Qin Hua，et al.Recommendation algorithm of combining clustering with collaborative filtering based on genetic algorithm［J］.Computer Technology and Development，2014，24（1）：35－38.（in Chinese）

［9］ Wang Ming－wen，Tao Hong－liang，Xiong Xiao－yong.A collaborative filtering recommendation algorithm based on iterative bidirectional clustering［J］.Journal of Chinese Information Processing，2008，22（4）：61－65.（in Chinese）

［10］ Yan Wei－min，Wu Wei－min.Data structures（C）［M］.1st edition.Beijing：Tsinghua University Press，2009.（in Chinese）

［11］ MacQueen J.Some methods for classification and analysis of multivariate observations［C］∥Proc of the 5th Berkeley Symposium on Mathematical Statistics and Probability，1967：281－297.

［12］ Dean J，Ghemawat S.MapReduce：Simplified data processing on large clusters［J］.Communications of the ACM，2008，51（1）：107－113.

附中文参考文献：

［3］ 尹航，常桂然，王兴伟.采用聚类算法优化的K近邻协同过滤算法［J］.小型微型计算机系统，2013，34（4）：806－809.

［5］ 曹波，苏一丹.基于蚁群聚类的top－N推荐系统［J］.微计算机信息，2009（9）：225－226.

［6］ 郁雪，李敏强.一种结合有效降维和K－means聚类的协同过滤推荐模型［J］.计算机应用研究，2009，26（10）：3718－3720.

［8］ 冯智明，苏一丹，覃华，等.基于遗传算法的聚类与协同过滤组合推荐算法［J］.计算机技术与发展，2014，24（1）：35－38.

［9］ 王明文，陶红亮，熊小勇.双向聚类迭代的协同过滤推荐算法［J］.中文信息学报，2008，22（4）：61－65.

［10］ 严蔚敏，吴伟民.数据结构（C语言版）［M］.第1版.北京：清华大学出版社，2009.