面向半物理仿真的陈述式模型求解方法研究*

熊 涛，丁建完，陈立平

（华中科技大学国家CAD支撑软件工程技术研究中心，湖北 武汉 430074）

面向半物理仿真的陈述式模型求解方法研究*

熊 涛，丁建完，陈立平

（华中科技大学国家CAD支撑软件工程技术研究中心，湖北 武汉 430074）

通过符号操作和数值计算相结合，提出了一种求解半物理仿真模型的新方法。为了满足半物理仿真对实时性的要求，在模型编译阶段将代表数值积分的隐式离散公式插入到仿真模型中，增广后的方程系统伴随着非线性方程的出现，需要在积分的每一步对这些非线性方程进行迭代求解，而求解非线性方程的时间复杂度随维度的变大成指数增加，因此引入代数环撕裂减小代数方程块耦合变量数，以满足实时求解对粒度的要求。最后通过实例对文中提出的方法进行了验证。

半物理仿真；微分代数离散；代数环撕裂；实时积分

1 引言

仿真技术是以相似原理、信息技术、系统技术及其应用领域有关的专业技术为基础，以计算机和各种物理设备为工具，利用系统模型对实际的或设想的系统进行试验研究的一门综合性技术。仿真技术应用广泛，从早期的航空、航天、火力发电和核动力发电部门扩展到今天的军事、电子、通信、交通、冶金、建筑、气象、机械、轻工等多种行业和部门，其应用已渗透到系统生命周期的全过程［1］。半物理仿真作为工程领域内一种应用广泛的仿真技术，涉及机电液控多个领域和学科。“半物理仿真”又称硬件在环仿真或物理—数学仿真［2］，是指针对仿真研究内容，将控制系统、被控制对象或系统部件用数学模型来描述，并转化为高速运行的实时仿真模型，然后与实物连接成为一个集计算机技术、数学建模技术及数据采集技术于一体的半物理仿真系统。然后借助物理效应模型，进行数学与物理的实时联合仿真，通过仿真试验对控制系统的控制策略、控制功能以及系统可靠性等进行测试和评估［3］。目前，半物理仿真已被广泛地应用于军事、汽车制造、工程机械和高校实验室建设领域。发展势头迅猛的多领域物理系统实时仿真主要应用方式就为半物理仿真，如减速箱［4］、柴油机控制［5］、汽车［6］、无 人汽 车［7］、锂 电 池［8］和 航 电模拟［9］等 。

本文对基于Modelica语言面向半物理仿真的陈述式模型实时求解算法进行研究，组织结构如下，首先对半物理仿真及其在工程实际中的应用进行简单介绍；其次对半物理模型的数学表达—微分代数方程DAEs（Differential Algebraic Equations）及其常用的求解方法进行分析，给出半物理仿真的难点；然后针对求解中的困难提出在模型编译阶段对DAEs进行离散，并对离散后能够缩减问题规模的代数环撕裂进行讨论；最后给出该方法的优势和展望。

2 微分方程求解方法

实时仿真在仿真软件应用领域发展的目标之一是能够以快速的采样率实时模拟越来越复杂的模型，满足半物理仿真的特性，也就是在很短的时间间隔内对物理模型的数学描述进行求解。工程中通常采用DAEs描述物理系统的动态特性和行为，DAEs通常由相互耦合的微分方程和代数方程混合而成，由于代数约束的存在，使DAEs的求解与常微分方程ODEs（Ordinary Differential Equations）产生了极大的不同，随着一系列特殊求解方法的提出，DAEs在工程实践中得到了广泛应用。其中，指标［10］是DAEs的一个重要属性，文献［11］对低指标问题进行了详细研究，高指标问题可以通过指标缩减转化为ODEs，指标缩减代表性的方法有：Gear方法［12，13］、Pantelides方法［14］和哑导方法［15，16］等。

微分方 程 的 求 解 方 法 分 为 变 步 长［17］和 定步长［18］两种，其中变步长方法需要在每个积分步对收敛性进行判断，且必须考虑求解精度对于步长的影响，效率较低。“硬件在环”是半物理仿真的显著特点，由于回路中接入实物，因此仿真是实时进行的，即仿真模型的时间比例尺和自然时间比例尺相同，同时受交互硬件固有频率的影响，使变步长算法在半物理仿真中的应用很困难。实际操作中半物理仿真往往使用定步长的方法，定步长算法又分为显式和隐式两种，对于常用的显式方法，当模型由机械、电气、液压或者热力组件耦合而成时，往往兼有快速和慢速子系统，导致仿真变成刚性问题，也就是说，模型中的时间常数具有较大的跨度，较快的时间常数决定仿真的计算量（步长），这将带来过多的计算量，降低了求解效率。使用隐式的求解算法虽然解决了数值稳定性问题，并且允许使用较大的步长，但求解精度制约着步长，而且使用隐式方法意味着由微分方程离散而来的非线性方程需要在每一积分步迭代求解，实时求解规模为n的非线性方程系统存在一定问题：操作的时间复杂度是O（n3），并且问题达到收敛所需的迭代次数可能随不同的步长而变动。综上，如何保证半物理仿真的实时性便成为一个重要的课题，除去仿真计算机自身的速度和精度，仿真模型的求解算法是影响仿真速度的一大重要因素，本文给出一种符号操作与数值计算相结合的半物理模型求解方法。该方法的基本思想为，使用代表求解方法的隐式公式在求解之前对DAEs进行离散，并借助相关符号操作实现求解的规划与分解，达到问题分而治之的目的。

3 DAEs的离散

在模型编译阶段将代表数值积分运算的隐式欧拉离散公式插入到方程系统中，实现指标约减后DAEs的增广，从而将连续问题预先转化为离散问题。完整约束的半仿真模型在指标约减后具有下面的表现形式：

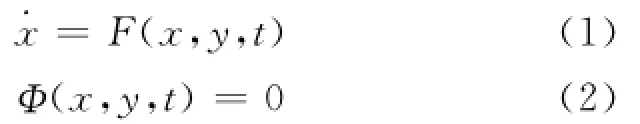
其中，E为微分方程，Φ为代数约束方程，x为状态变量，y为代数变量，假设在一致性初始条件x（t0）= x0，˙x（t0）=x0，y（t0）=y0下，具有唯一且光滑的解［17］。

DAEs离散步骤：

步骤1 根据是否具有微分形式将变量划分为集合x和集合y，满足dim（W）=dim（x）+dim （y），W=［x，y］。

步骤2 为保证方程系统的恰定性，取x为已知量，˙x和y为未知量，对DAEs进行强连通分量SCC（Strongly Connected Components）凝聚［19］，以及拓扑排序，从而可以得到顺序求解的方程子集序列。

步骤3 就xi而言，若˙xi可通过匹配的方程显式地求解出来，则向DAEs中添加如下的离散方程：

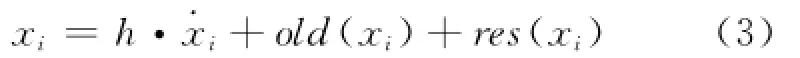
其中res（xi）表示将xi当作撕裂变量，以迭代的方式求解xi。

若˙xi无法显式求解，向DAEs中添加：

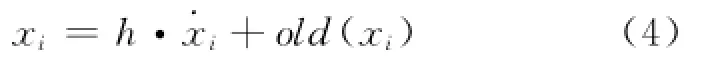
步骤4 若与˙xj或者yk匹配的赋值形式方程en处于代数环中，即结构关联矩阵中所处的对角块维度超过1，则在en的表达式中添加一个新项res（˙xi）或者res（yk），标记为撕裂变量，即：

步骤5 如果res（xi）、res（˙xj）或是res（yk）所处的代数环不能被撕裂，则移除相应的res（）操作符。

步骤6 以x、˙x和y为未知量，重新对离散后的DAEs进行SCC凝聚和拓扑排序，从而可以得到顺序求解的方程子集序列。

下面通过一个简单的例子进行说明。

其中，ω、D和k为常数，f和g为函数，x、x1和x2为 微 分 变 量，u和y为 代 数 变 量。若 使 用DASSL［17］直接求解，则需对全部的5个变量进行迭代。DAEs离散方法处理如下：由于微分变量˙x、˙x1和˙x2均具有显式表达，所以使用下面的离散公式（8）～公式（10）对式（7）进行增广：

增广后的DAEs如下：

就式（11）而言，为保证方程的恰定性需同时将˙x、˙x1、˙x2、x、x1和x2视为未知量，消去增广式中的微分变量˙x、˙x1和˙x2，得：

式（12）的二部图最大匹配及SCC凝聚如图1和图2所示，图1中双向边代表最大匹配，其中需要注意的是式f4中的x1，可以通过式f3转换为关于x2的表达。

Figure 1 Direct constraint graph¯G of equ.（12）图1 式（12）的约束有向图¯G

Figure 2 Cohesion graph¯C of SCC¯G图2 ¯G强连通分量凝聚图¯C

图2中，强连通分量C1=｛f1|x｝、C2=｛f2|y｝、C3=｛f3|x1｝、C4=｛f4|x2｝和C5=｛f5| u｝，这5个强连通分量构成了代数环，当选择变量x作为撕裂变量，反映在图中为切断强连通分量C1和C2之间的有向弧，可得顺序求解的方程序列C2→C4→C3→C5→C1，方程求解顺序与图¯C中有向弧的方向相反。

观察式（13）可知，只需要对变量x进行迭代，即可实现方程的求解，所以移除标记res（x1）和res（x2）。同理，可选择变量x1或x2作为撕裂变量。下面介绍对于缩减问题规模具有重要意义的代数环撕裂。

4 代数环撕裂

为了减小DAEs离散后非线性求解块的粒度，使用代数环撕裂作为后处理，以提高求解效率。代数环撕裂的基本思想：利用代数环结构上的稀疏性，通过切断某些耦合关系，将某些方程转化为赋值等式的形式，从而缩减需要联立求解部分的规模，提高求解效率。考虑一般形式的方程组，如式（14）所示：

式（14）为三个相互耦合的方程，约束表示图如图3a所示，这三个方程组成了一个强连通分量。撕裂该代数环的符号操作为：打断组成强连通分量中的某条边，检查图中是否存在新的强连通分量，若存在，继续上述的操作；否则，结束。需要注意的是，每打断约束表示图中的一条边，为保证方程系统的恰定性，需要引入一个辅助方程和辅助变量，如图3b所示。

Figure 3 Direct graph of equ.（14）图3 式（14）的有向表示图

依次打断边（f1，x1）和（f2，x2），得到图3b所示的形式，方程f'1和变量x'1是打断边（f1，x1）时引入的辅助方程和辅助变量，f'2和x'2是打断边（f2，x2）时引入的辅助方程和辅助变量，符号操作后的式（14）可以通过下面的计算过程求得：

BEGIN

LOOP

UNTIL|x'1—x1|＜εAND|x'2—x2|＜ε

END

fi_calc_xi表示通过方程fi计算变量xi，ε表示迭代收敛所允许的误差。

下面给出代数环撕裂的一般方法，假设代数环具有式（15）指定的形式：

撕裂就是从代数环中分离出一部分方程和变量，即｛g1|g1∈g｝和｛z1|z1∈z｝。假定z1为已知量，可由剩余的方程｛g2|g2∪g1=g｝，依次求解剩余的变量｛z2|z2∪z1=z｝。可以通过牛顿法求解分裂后的方程系统，该过程描述如下：

步骤1 选择合适的撕裂变量z1，并赋初值z1（0）；

步骤2 通过剩余的方程g2求出z2，即z2= g2（z1）；

步骤3 计算残差δ=g1（z1，z2）；

步骤4 若δ小于收敛误差ε，结束，否则，转步骤2。

通过代数环撕裂，可以将耦合方程的维数从dim（h1）+dim（h2）减小到dim（h1）。然而就撕裂过程而言，选出合适的z1是十分困难的，不同的选取方式会带来计算量和误差上的差异，同时在实际操作中必须考虑初值z1（0）以及h1（z1，z2）迭代的收敛性。为此，采用的方法是取DAEs离散后标记为res的变量作为撕裂变量，来验证能否达到代数环撕裂的目的。

5 实例分析

本文提出的方法在多领域建模与仿真平台MWorks［20］中进行实验，下面通过笛卡尔坐标系下三自由度挖掘机的转臂模型进行验证。

转臂由包括R1、R2、R3、R6、R7、R8、R9、R11、R12、R13、R14、R15和P4、P5、P10在内的12个转动副和3个移动副组成，为使存在环路的模型可解，取R6、R8、R11、R14为切割铰。记r表示R. phi，用以描述转动副的相位转角；p表示P.s，描述移动副的伸张长度。指标约减后选择r7、r12、r15作为状态变量的DAEs具有下面的表现形式：

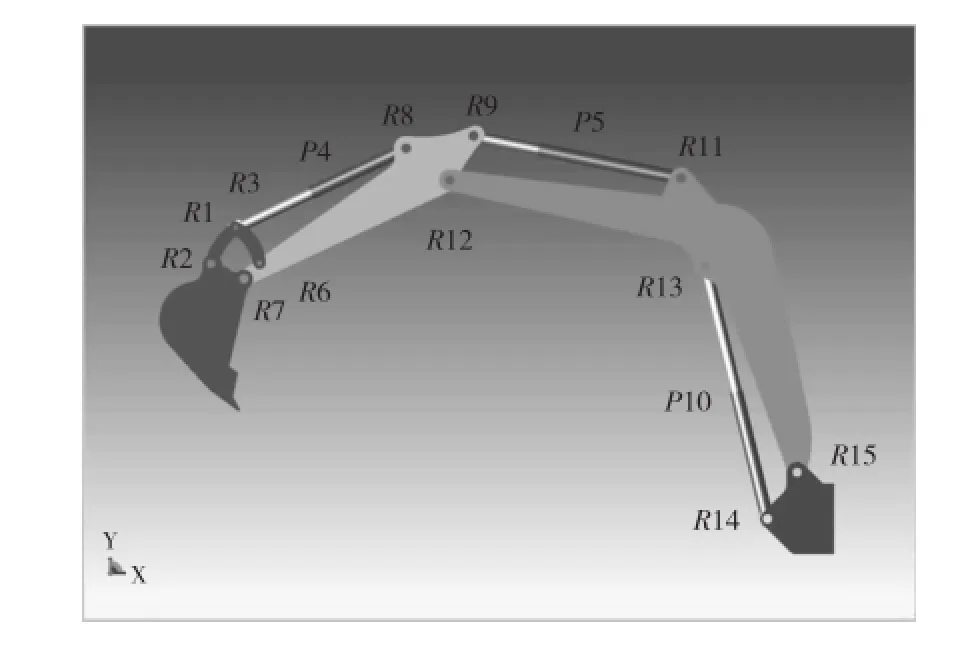
Figure 4 Excavator jib model with three degrees of freedom图4 三自由度挖掘机的转臂模型

Figure 5 Directed constraint graph of augmented DAEs图5 转臂模型增广DAEs的有向约束图h

Figure 6 Cohesion graph¯Chof SCCh图6的强连通分量凝聚图

由图6可得各强连通分量中需要联立求解的变量数分别为5、3和3，求解顺序为→→，将各强连通分量中标记为res的变量作为撕裂变量执行代数环撕裂，均可以获得迭代变量数为1的求解序列，如下所示：

使用隐式欧拉法对该模型进行求解，对比一般方法（需对11个变量同时进行迭代）和文中提出的方法，仿真时间均为10 s，表1给出了不同方式下积分时间的对比。

Table 1 Comparison of different methods in solving time表1 不同方式求解时间对比

采用DAEs离散和代数环撕裂的方法能够满足实时性的要求（7.35 s＜10 s），同时为了保证提出方法的正确性，图7给出r2的仿真结果对比。

Figure 7 Simulation results of r2in two ways图7 两种方式下r2仿真结果对比

就转臂模型而言，借助DAEs离散和代数环撕裂将需要联立求解的模型（迭代变量数为11）转化为三个代数方程块的顺序求解，且每个方程块的迭代变量数为1，并且数值积分时间小于模型仿真时间，能够满足半物理仿真的要求。

6 结束语

本文主张在模型编译阶段采用隐式欧拉法对DAEs进行离散，并通过代数环撕裂来减小增广后的方程系统规模。绝大多数情况下本文提出的方法能够将整个方程系统分解为多个可单独迭代求解的子系统，从而提高求解效率，满足半物理仿真的要求，并通过实例分析验证了该方法的正确性。总的来说，只有在离散后的代数环无法撕裂的情况下，所需迭代的变量数才与通用积分方法相等。在未来的研究中希望能够对仿真模型中的快速状态与慢速状态进行区分，从而能够在DAEs的离散中使用显式的离散公式。

［1］ Liu Rui-ye.Elements of computer simulation［M］.Beijing：Publishing House of Electronics Industry，2011.（in Chinese）

［2］ Aranya C，Xin Yu-feng.Hardware-in-the-loop simulations and verifications of smart power systems over an exo-GENI testbed［C］∥Proc of the 2nd GENI Research and Educational Experiment Workshop，2013：16-19.

［3］ Kang Feng-ju，Yang Hui-zhen，Gao Li-e.Technology and application of modern simulation［M］.Beijing：National Defense Industry Press，2006.（in Chinese）

［4］ Casella F，Donida F，Lovera M.Beyond simulation：Computer aided control system design using equation-based object oriented modeling for the next decade［C］∥Proc of the 2nd International Workshop on Equation-Based Object-Oriented Languages and Tools，2008：35-45.

［5］ Song Bai-ling.Semi-physical simulation technology research of diesel electronic control system［D］.Harbin：Harbin Engineering University，2009.（in Chinese）

［6］ Mattsson S E，Elmqvist H，Otter M.Physical system modeling with Modelica［J］.Control Engineering Practice，1998，6 （4）：501-510.

［7］ Tang Guo-ming.Design of hardware-in-the-loop simulation system for driverless vehicle［D］.Hefei：University of Science and Technology of China，2012.（in Chinese）

［8］ Luciano S，Ines C，Manuela G.A design methodology for semi-physical fuzzy models applied to the dynamic characterization of LiFePO4 batteries［J］.Applied Soft Computing，2014，14（B）：269-288.

［9］ Jiang Zhan-si.Parameter optimization and inference solving for models based on Modelica［D］.Wuhan：Huazhong University of Science&Technology，2008.（in Chinese）

［10］ Unger J，Kröner A，Marquardt W.Structural analysis of differential-algebraic equation systems-theory and applications ［J］.Computers&Chemical Engineering，1995，19（8）：867-882.

［11］ Negrut D，Jay L O，Khude N.A discussion of low order numerical integration formulas for rigid and flexible multibody dynamics［J］.ASME Journal of Computational and Nonlinear Dynamics，2007，4（2）：1-11.

［12］ Gear C W，Petzold L R.ODE methods for the solution of differential/algebraic systems［J］.SIAM Journal on Numerical Analysis，1982，21（4）：716-728.

［13］ Gear C W.Differential-algebraic equation index transformations［J］.SIAM Journal on Scientific and Statistical Computing，1988，9（1）：39-47.

［14］ Pantelides C C.The consistent initialization of differentialalgebraic systems［J］.SIAM Journal on Scientific and Statistical Computing，1988，9（2）：213-231.

［15］ Mattsson S E，Söderlind G.Index reduction in differentialalgebraic equations using dummy derivatives［J］.SIAM Journal on Scientific Computing，1993，14（3）：677-692.

［16］ Feehery W F，Barton P I.A differentiation-based approach to dynamic simulation and optimization with high-index differential-algebraic equations［C］∥Proc of the 2nd International Workshop on Computational Differentiation，1996：239-252.

［17］ Brenan K E，Campbell S L，Petzold L R.Numerical solution of initial-value problems in differential-algebraic equations ［M］.Philadelphia：SIAM，1996.

［18］ Mathews J H，Fink K K.Numerical methods using Matlab ［M］.London：Prentice Hall，2004.

［19］ Xavier A.On the complexity of strongly connected components in directed hypergraphs［J］.Algorithmica，2014，69 （2）：335-369.

［20］ http：∥www.tongyuan.cc/.

附中文参考文献：

［1］ 刘瑞叶.计算机仿真技术基础［M］.北京：电子工业出版社，2011.

［3］ 康凤举，杨惠珍，高立娥.现代仿真技术与应用［M］.北京：国防工业出版社，2006.

［5］ 宋百龄.柴油机控制系统半物理仿真技术研究［D］.哈尔滨：哈尔滨工业大学，2009.

［7］ 唐国明.无人驾驶汽车半物理仿真系统设计［D］.合肥：中国科学技术大学，2012.

［9］ 蒋占四.Modelica仿真模型的参数优化及推理求解研究［D］.武汉：华中科技大学，2008.

熊涛（1990），男，河南确山人，博士生，研究方向为多体系统动力学、多领域建模与求解。E-mail：xiongtao39@163.com

XIONG Tao，born in 1990，Ph D candidate，his research interests include dynamics of multibody systems，multi-domain modeling and solving.

A method for solving semi-physical simulation declarative models

XIONG Tao，DING Jian-wan，CHEN Li-ping
（National CAD Support Software Engineering Research Center，Huazhong University of Science and Technology，Wuhan 430074，China）

We propose a new method for solving semi-physical simulation models using a mixed symbolic and numeric approach.In order to meet the real-time requirement of semi-physical simulations，implicit discretization formulae representing the numerical integration algorithm are inserted into the DAEs symbolically at compile stage.Then nonlinear equations will appear in the augmented equation system and all these nonlinear equations should be solved together at each integration step.In order to meet the fine granularity required for solving the models in real-time，tearing algebraic loop is introduced.After that the dimensions of nonlinear equation blocks can be reduced as the time complexity of calculating nonlinear equations increases exponentially with the growth of dimensions.Finally，an example is given to show that the proposed method is not only easy to implement but also efficient.

semi-physical simulation；discrete DAEs；tearing algebraic loops；real-time integration

TP301

A

10.3969/j.issn.1007-130X.2015.08.018

1007-130X（2015）08-1540-06

2014-06-27；

2014-10-11

国家科技支撑计划资助项目（2012BAF16G02）

通信地址：430074湖北省武汉市华中科技大学国家CAD支撑软件工程技术研究中心

Address：National CAD Support Software Engineering Research Center，Huazhong University of Science and Technology，Wuhan

430074，Hubei，P.R.China