基于SAM-CS和SOFM的胃上皮肿瘤细胞图像识别*

甘 岚，孙开杰，谢丽娟

（华东交通大学信息工程学院，江西 南昌 330013）

基于SAM-CS和SOFM的胃上皮肿瘤细胞图像识别
*

甘 岚，孙开杰，谢丽娟

（华东交通大学信息工程学院，江西 南昌 330013）

针对胃上皮肿瘤细胞图像（以下简称肿瘤细胞图像）黏结严重和信息冗余的特点，提出了一种将自适应观测矩阵的压缩感知（SAM-CS）和自组织特征映射（SOFM）神经网络相结合的算法。该算法将肿瘤细胞图像拉成列向量，然后利用通过自适应过程产生的观测矩阵，基于压缩感知理论对图像信息进行观测，产生线性观测向量，最后利用SOFM神经网络的学习算法对观测向量进行训练和分类，实现对肿瘤细胞图像的识别。实验表明，相比常用算法，该算法至少提高了4.2%的识别准确率和5.7%的运算速度。

自适应观测矩阵；压缩感知；自组织特征映射；肿瘤细胞图像识别

1 引言

肿瘤细胞图像是一种特殊的自然图像［1］，一是细胞组织器官形状不规则且不同细胞类之间存在较大的差异性和黏结性；二是图像数据的高阶统计特性服从非高斯分布，意味着图像中含有大量的冗余信息；三是数据样本较少。因此，采用一般的形

态特征提取方法和线性分类算法会出现提取困难、计算时间长、分类错误等问题［2］。常用的特征提取方法［3］有：PCA、DCT、FFT和LDA，这些算法多应用于标准或规则纹理图像，而肿瘤细胞图像背景复杂，干扰严重，应用常用算法存在计算量大和效果不佳的问 题。常用的识别分类 算法［4］有：SVM和贝叶斯分类算法。SVM具有分类准确度高和时间复杂度低的优点，但是处理大型数据集时，速度严重降低。贝叶斯分类算法对于大型数据集，从理论上讲，精确度高，运算速度快，具有最小的错误率，但实际情况下，因其假定的不准确性，导致缺乏可用的数据，就需要足够大的样本。

压缩感知也称压缩传感或压缩采样，其核心思想是在信号采样的同时实现信息的压缩，它突破了香农定理对信号采样频率的限制。近年来，随着压缩感知理论的发展，压缩感知理论在模式识别领域也得到了广泛的应用。威斯康辛大学相关学者［5］运用压缩感知从欠采样投影数据矩阵中准确重构动态CT图像。国内方面，任丛林等［6］基于压缩感知算法的基因表达谱数据分析对疾病的临床诊断和生物信息学研究有重要的参考和借鉴作用。

针对肿瘤细胞图像复杂、冗余大、样本少的特点，本文提出了一种基于SAM-CS（Self-Adaptive Measurement matrix-Compressed Sensing）和SOFM（Self-Organizing Feature Map）的肿瘤细胞图像识别算法。本算法首先利用压缩感知理论，设计自适应的观测矩阵，通过观测矩阵对肿瘤细胞图像投影，提取出代表图像的特征基信息；然后利用SOFM神经网络学习算法，对分类模型进行反复训练学习，最终实现样本的分类识别。实验表明，与前面几种特征提取和分类算法相比，本文提出的算法对于肿瘤细胞图像来说，具有更高的准确率和效率。

2 基于自适应观测矩阵的压缩感知算法

2.1 压缩感知数学模型

压缩感知理论（CS）［7，8］指出：只要信号X在领域RN通过某种变换（如傅里叶变换、小波变换等）后能够是稀疏的或可压缩的，那么就可以利用不相关的矩阵对其进行投影，再利用这些少量的投影值求解一个优化问题，最后能够以一个高概率重构出原始信号。经过观测矩阵投影后，信号X由N维减少到M维（M≪N），其中这M个观测值仅仅包含该信号的重要相关信息。下面给出压缩感知的数学模型表示方法。

考虑把RN领域的一个长度为N的信号X视为一个N×1的一维列向量（其中的元素由Xi表示，i=1，2，…，N）。由信号理论可知，RN空间中的任意一个信号可以由正交稀疏基向量Ψ的线性组合表示，得到：其中，αi=，xi表示一维向量X的第i个元素值，Ψ为信号X的稀疏基矩阵，α与X均为N× 1矩阵，Ψ为N×N矩阵。

从公式（1）可以看到，X和α等同于一个信号，不同点是它们分别是不同域的表示，X是信号在RN域的表示，α则是信号在Ψ域的表示。α是一个只包含K≪N个非零值的展开系数，则认为信号在Ψ域是K-稀疏的。

那么，设计一个与稀疏基矩阵 Ψ不相关的M×N随机观测矩阵Φ对于获取采样很重要，通过式（2）将稀疏信号在观测矩阵Φ上进行投影，得到一个比原始信号长度小得多的 M×1的线性观测向量Y，使观测对象由N维降到M维。其中，=ΦΨ称为CS信息算子，M×N维大小的矩阵Φ定义为观测矩阵（M≪N）。文献［9，10］提出，观测矩阵具有有限等距性质RIP（Restricted Isometry Property），是公式（2）存在确定解的充要条件。

综上所述，压缩感知理论就是通过采集到的经过观测矩阵Φ变换的观测集合Y来重构出原始信号X的全部信息。

2.2 自适应方式产生观测矩阵的算法

然而压缩感知理论依赖于两个原则：稀疏性和不相关特性，稀疏性由信号本身决定，不相关特性由感知系统决定。为了提高感知系统的不相关特性，Elad C［11］提出一个通过自适应方式产生观测矩阵的算法。这个算法不需要对数据集统计进行假设，只是需要假设已经提供充分完备的稀疏基Ψ，依赖稀疏基Ψ设计观测矩阵Φ，提高观测矩阵Φ与其的不相关性，减少投影的重建错误。

这里处理不相关特性的方法，就是把等价字典D=ΦΨ假设为格拉姆矩阵 ，即，此处，是列正则化后的等价字典D。

具体想法是最小化相应的格拉姆矩阵非对角值的最大绝对值，同时保持等价字典的秩满足M≪N，需要解决的问题是使D任何列的子集尽可能正交，或者可以说是G要尽可能地接近单位矩阵。而目标就是保证满足RIP性质，确保压缩感知的鲁棒性和稀疏性。

根据前面提到的，考虑目前的稀疏基Ψ是已知的。本文使用将等价字典D=ΦΨ接近格拉姆矩阵的方式求得观测矩阵Φ。得到如下等式：由此得到：

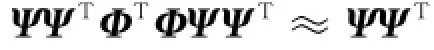
然后，对ΨΨT进行特征值分解，求前r个非零特征值。令VΛVT是ΨΨT的特征值分解，即VΛVT= ΨΨT，其中，Λ是对角矩阵，对角线上的值为特征值分解的特征值，V是对应的特征向量矩阵，因此得到VΛVTΦTΦVΛVT≈VΛVT。并令Γ=ΦV，从而得到ΛΓTΓΛ≈Λ。所以，计算更新Φ时，只需使Λ—ΛΓTΓΛ矩阵的2-范数最小化，即公式（3）最小。令λ1，…，λN为对角矩阵Λ对角线上的值，即ΨΨT的特征值，［τ1，…，τM］T构成Γ矩阵，将公式（3）转换成更容易求其零误差的目标函数矩阵：

其中vi=［λ1τi，1，…，λNτi，N］T。

矩阵转换为：

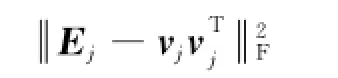
令UjΔjUjT是Ej的特征值分解，即Ej= UΔUT，求解E特征值及特征向量，并且特征值

jjjj

按大小排列，取最大特征值为ξ1，j，对应特征向量u1，j，则目标矩阵进一步转换为：

如果现在将求2-范数最小化转换为求vj=的解，E中的最大错误组件就会被消除。用前面最优化的矩阵行值τj来替换vj，得到派生式（4）：

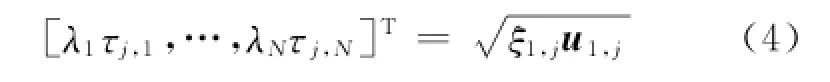
由于对角矩阵Λ通常不是满秩矩阵，当r＞0时，λN—r+1，…，λN将为零，因此只需要更新τj的组成τj，1，…，τj，N—r。所以，派生式（4）成为本文优化

算法的基础。由公式得到的τj，1，…，τj，N—r得到；通过更新得到很容易由=V得到，即=VT。

3 SOFM神经网络算法

3.1 SOFM神经网络模型

SOFM神经网络［12］是芬兰Kohonen教授提出的一种竞争型神经网络模型，它主要包括了输入层和竞争层两个部分。其中输入层对应于样本空间，负责接收来自外界输入的矩阵变量X=［［X1，X2…，Xp］，其中，Xp=［x1p，x2p，…，xnp］T，p∈［1，2，…，P］；而竞争层则是由多个神经元j组成的一维或二维的平面阵列，该层神经元之间形成竞争关系，并采取“胜者全得”的策略，即竞争层的所有神经元输出中，只有一个神经元j*的输出不为0。与其它网络不同，该网络的竞争层神经元不仅接收来自输入层神经元的直接输入，同时接收来自同一层网络的反馈输入，即侧向交互。这种同层网络的侧向交互主要遵循以下两点：（1）以获胜神经元j*为中心，对指定大小邻域Nj*（t）内的神经元表现为兴奋性侧交互，即将近邻神经元的权值向量朝着神经元j*方向调整，使之在下次输入同类模式的时候，能够增加获胜机会；（2）以获胜神经元j*为中心，对指定大小邻域 Nj*（t）外的神经元表现出抑制性侧交互，即不调整其权值，使得当再次输入同类模式的时候，减少获胜的机会。

在SOFM网络进行分类时，输入数据xip，xip表示矩阵变量第i行第p列的元素值，若神经元j*产生最大响应，则将该样本归为j*神经元，即j*为获胜神经元；当输入的数据xip不属于训练过程中的任一模式时，则按照最近邻原则，将其归为最接近的类别。3.2 SOFM网络的学习算法

SOFM神经网络的学习算法［13］被称之为Kohonen算法，下面是学习算法的具体过程。

首先初始化SOFM网络，根据待学习观测样本X的输入模式集种类，确定竞争层的神经元个数及其排列方式。然后按照一定的策略，初始化竞争层中各神经元的权值向量，并对权值向量进行归一化处理，得到，j=1，2，…，m。最后对初始优胜邻域 Nj*（0）的大小进行确定，给出网络的学习率η初始值。

从训练样本X=［X1，X2，…，Xp］中随机选取一个输入模式Xp=［x1p，x2p，…，xnp］T输入初始化后的SOFM神经网络，按公式（5）计算Xp和所有的权值向量wj的欧氏距离，其中欧氏距离最小的为获胜神经元j*。

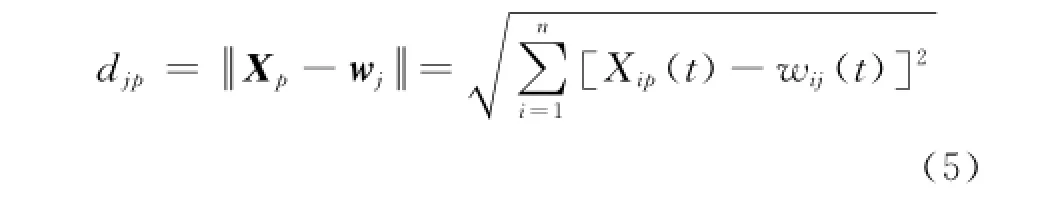
确定以获胜神经元j*为中心的权值调整邻域的范围Nj*（t）。通常情况下，网络的初始获胜邻域 Nj*（0）会比 较大，但 随着训 练次 数的 不 断增加，权值调整邻域的范围 Nj*（t）也会逐渐缩小。

根据邻近区域，对优胜邻域 Nj*（t）内的所有神经元进行权值调整，在网络训练过程中，网络权值的调整是与获胜神经元之间的距离变化有关，是随着距离变化而逐渐衰减的，对所有在 Nj*（t）中的神经元权值采取公式（6）进行调整：其中，wi，j（t）表示当前t时刻的竞争层神经元j与输入层神经元i之间的权值，wi，j（t+1）为权值调整后的结果，η（t）表示训练时间t的学习速率值，一般η（t） 为单调递减函数，且有0＜η（t）＜1。

而对于优胜邻域 Nj*（t）以外的神经元，其权值不进行调整即权值不变。

重复执行将训练样本模式集中不同数据随机输入SOFM神经网络进行学习的过程，当网络的学习速率η（t） 的值减少为零或小于某个指定的阈值时，整个学习过程结束。

4 基于SAM-CS和SOFM的肿瘤细胞图像分类识别算法

4.1 算法模型

对于具有结构差异和严重黏结现象的肿瘤细胞图像而言，使用常用的特征提取和分类算法识别率和运算速率都较低，基于SAM-CS算法和SOFM神经网络分类识别算法相结合的肿瘤细胞图像识别算法可以改善这个问题。

首先，肿瘤细胞图像的差异性和黏结性导致图像存在复杂的冗余信息，这些冗余信息会严重影响肿瘤图像的识别。采用SAM-CS算法抛弃了当前采样信号中的冗余信息，能够尽可能地提取肿瘤细胞图像的特征，克服了常用特征提取方法受图像差异性和黏结性影响的缺陷。

其次，SOFM神经网络考虑了生物神经元的空间组织性，能够充分模拟人脑视觉神经元的分类方法，反映了大脑神经细胞的记忆方法以及神经细胞被刺激时的兴奋规律等一系列生物神经系统的特点，能够自适应地实现对外界输入刺激的聚类分析。其独特的拓扑结构保持能力和概率保持特性，能够合理解决肿瘤细胞图像结构差异的问题，这是常用分类识别算法所不具备的。

由上所述，同时考虑SOFM神经网络受初始样本的影响不大，本文提出基于SAM-CS算法和SOFM神经网络分类识别算法结合的肿瘤细胞图像识别算法模型，如图1所示。

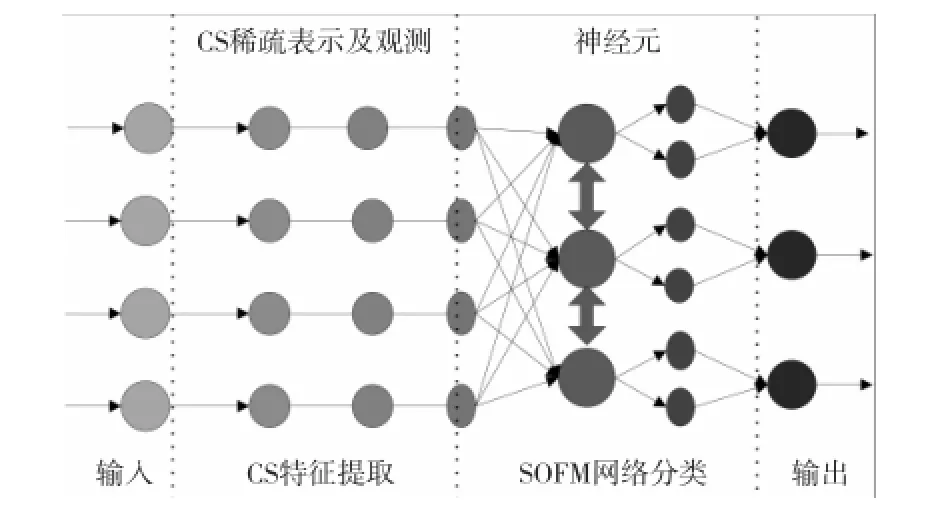
Figure 1 Recognition algorithm model图1 识别算法模型

由图1可以明显看出，该识别算法模型分为两层：第一层为自适应观测矩阵的压缩感知（SAMCS）用于特征提取阶段。在对图像数据进行归一化处理后，采用压缩感知中的自适应观测矩阵对数据进行观测，优化之后得到的观测矩阵与稀疏矩阵之间有更低的相关性，使压缩感知特征提取出更能代表图像的特征基信息。第二层是自组织特征映射（SOFM）的分类神经网络，该层网络接收来自第一层特征提取后的特征基，运用SOFM神经网络的学习算法，对分类模型进行反复训练学习，最终达到对测试样本分类识别为正常细胞图像、增生细胞图像和癌变细胞图像三类的目的。

4.2 肿瘤细胞图像识别算法流程

基于上面提到的识别算法模型，先利用SAMCS去除冗余信息的特点，使用自适应的观测矩阵对归一化后的肿瘤细胞图像数据进行观测，得到肿瘤细胞图像的特征基；然后将训练样本特征基输入SOFM神经网络进行自适应训练，保存训练后的网络结构；最后将测试样本的特征基输入训练结束的SOFM神经网络，完成对测试样本的分类。成功通过分类测试的模型即为所需的分类模型，输入数据就可以用来达到分类识别的目的。本算法的具体流程图如图2所示。

4.3 肿瘤细胞图像识别工作算法

结合前面的识别算法模型图1和流程图2，得到肿瘤细胞图像识别算法的具体工作算法如下：

步骤1 输入s幅b×d维大小的肿瘤细胞图像，其中s/2幅选定为训练样本X=［x1，x2，…，xs/2］，剩余的选定为测试样本Y=［y1，y2，…，ys/2］。

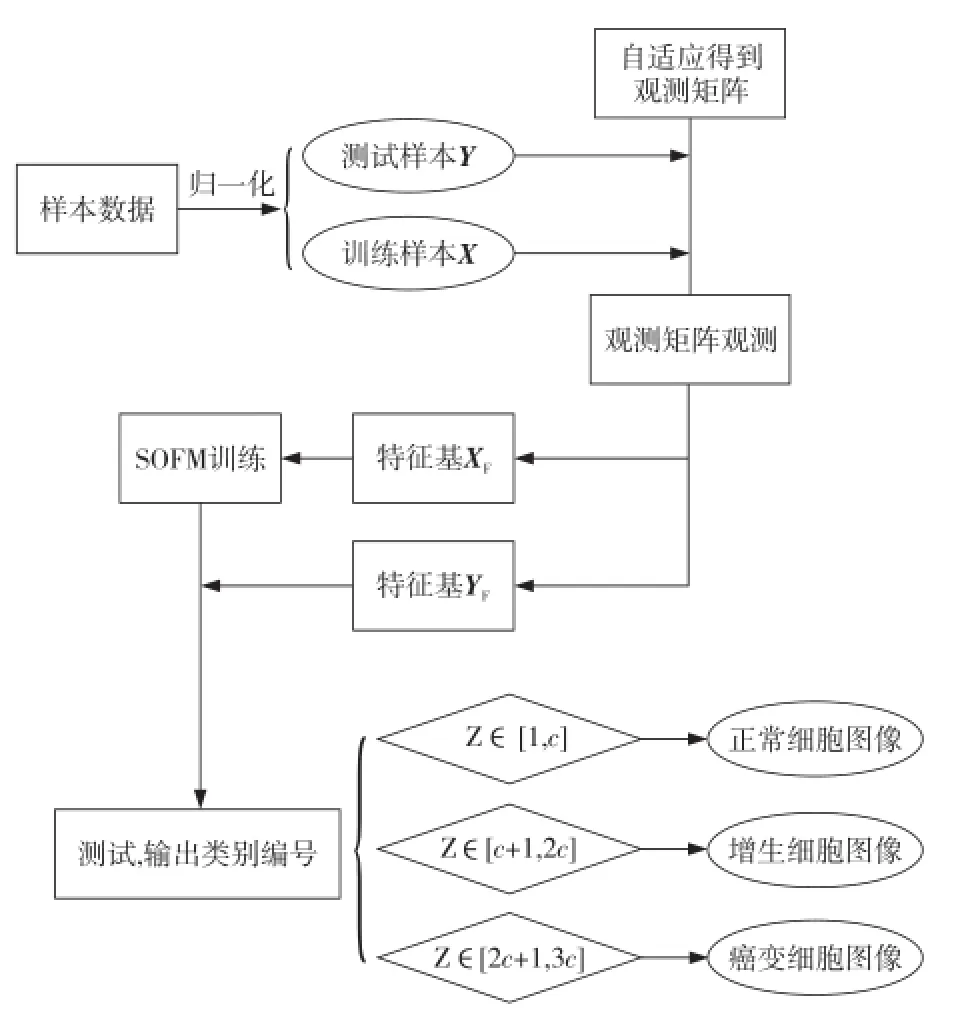
Figure 2 Recognition algorithm图2 识别算法

步骤2 对X、Y图像矩阵进行归一化处理，把归一化处理后的肿瘤细胞图像矩阵拉成列向量xi=［xi1，xi2，…，xiN］T和 yi= ［yi1，yi2，…，yiN］T（N=b×d）。

（1）初始化Φ，产生M×N（M≪N）维初始高斯随机矩阵Φ。

（2）对字典ΨΨT进行特征分解，即VΛVT= ΨΨT，并计算其非特征值的数量r。

（3）初始化Γ=ΦV。

（4）j=1，…，M：

①计算Ej特征值及特征向量；

②寻找Ej的最大特征值和对应特征向量；

步骤5 初始化SOFM神经网络，设定初始权值wi，j为较小的随机数。图像包含正常、增生和癌变三类图像，因此设计SOFM竞争层的输出神经元为3c个，每个类别对应有c个神经元，同一类别的c个神经元排列在相对邻近的拓扑区域内。

步骤6 将步骤4中得到的向量矩阵XF作为初始化后 SOFM网络的训练样本特征基，根据SOFM的学习算法，设定不同的步数对网络进行训练，通过权值的不断调整，待网络稳定后保存网络参数值用以测试。

步骤7 将在步骤4中得到的向量矩阵YF作为测试样本特征基，输入保存的网络中，输出获胜神经元的编号Z。根据输出的获胜神经元编号，最终实现测试样本图像的类别判定。

5 实验过程与结果分析

从医学病理的角度上，依据细胞的形状、排列规则、密度、纹理等特征分析可知，胃上皮肿瘤细胞图像大致上可以分为三大类：正常、增生和癌变。其中，针对增生细胞图像，根据增生程度的不同，又可将其分为轻度增生细胞图像、中度增生细胞图像和重度增生细胞图像三类，如图3所示。正常细胞图像的腺管结构形状轻度规则、整齐、排列密度较均匀；腺体排列整齐而规则，方向一致并按层疏松排列；细胞大小一致，单个细胞呈圆形。增生细胞图像的腺管结构形状不规则、大小不整齐、迂回曲折；而轻度增生的细胞呈柱状，细胞核密集；中度增生细胞的细胞核相对变大，排列稍显紊乱；重度增生细胞的细胞核有分裂现象。癌变细胞图像中细胞弥散化，细胞组织器官形状完全不规则，腺管结构几乎不存在。

在实验过程中，本文选取300幅320*240维的肿瘤细胞图像作为实验样本，其中训练样本和测试样本各150幅。而训练样本和测试样本中正常细胞图像、增生细胞图像和癌变肿瘤细胞图像各50幅。利用这些样本数据，分别进行观测次数对比实验、观测矩阵相关性实验、特征提取效果对比实验和识别算法对比实验。

5.1 观测次数对比实验

使用不同观测矩阵对样本数据进行观测时，所需观测次数越少反映了该观测矩阵下压缩感知的工作效率越高。图4选取Fourier观测矩阵、高斯随机矩阵及本文的自适应观测矩阵对比，信号稀疏度固定为55。

由图4看出，采用自适应观测矩阵对样本数据稀疏基进行观测，相对误差迭代至稳定时所需观测次数为90，而高斯随机矩阵和Fourier矩阵分别为100、120。自适应观测矩阵大大优于Fourier观测矩阵，凸显了自适应观测矩阵的效率优势。

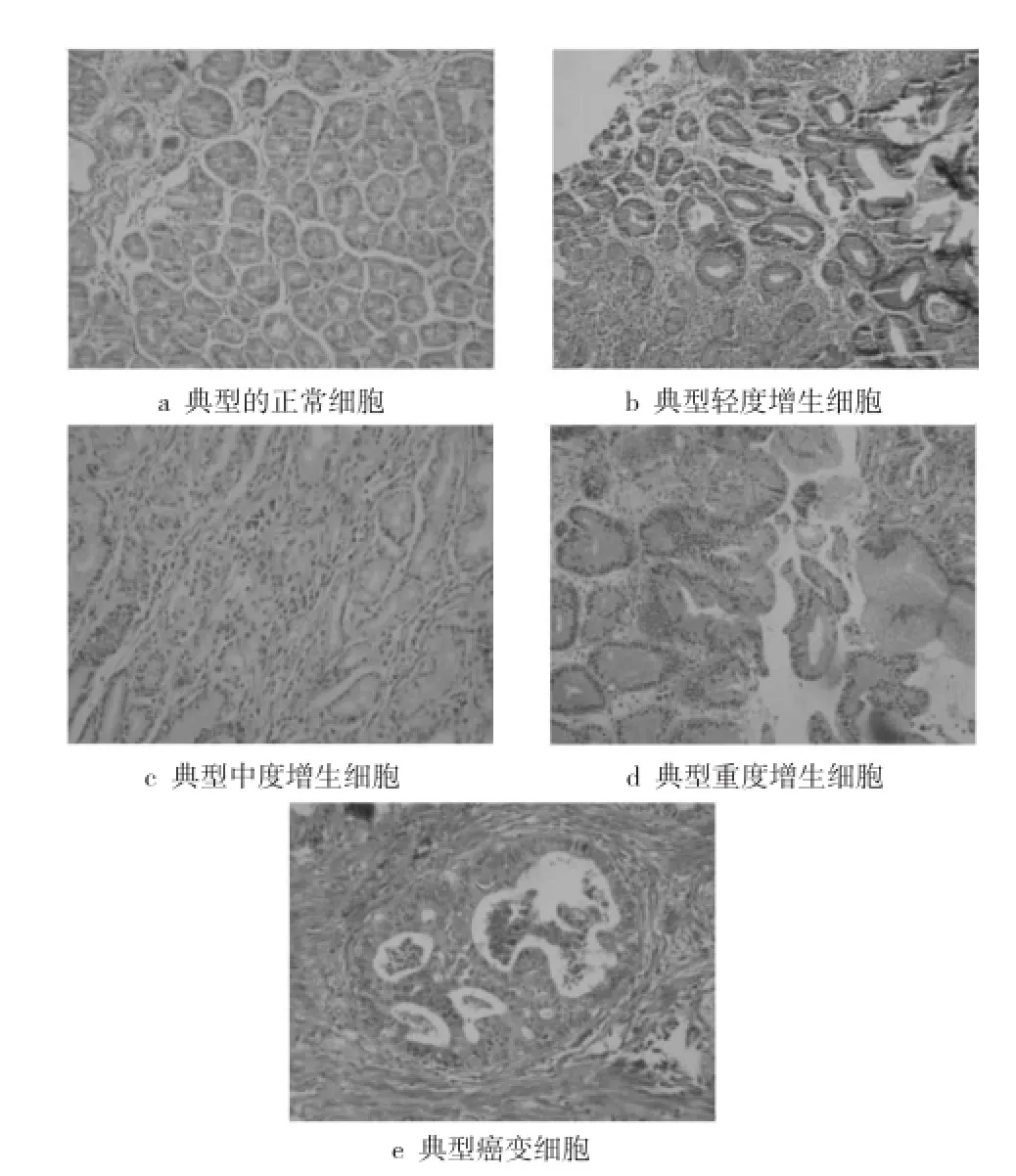
Figure 3 Images of different kinds of gastric epithelium tumor cell图3 不同类别的胃上皮肿瘤细胞图像

Figure 4 Relation diagram between relative error and the number of measurement of different measurement algorithms图4 不同观测矩阵重建的相对误差与观测次数关系图

5.2 观测矩阵相关性实验

压缩感知中选择观测矩阵的重要原则是要求其与稀疏基具有不相关性或较小相关性，才能保证经过观测后所得的观测值矩阵能准确地重构出原图像。为此，对不同观测矩阵进行了相关性实验对比。实验以观测次数步长为10，从40逐渐增加到120，稀疏基采用离散余弦变换DCT（Discrete Cosine Transform）稀疏变换，实验结果如表1所示。

Table 1 Correlation parameters between different measurement matrixes and the sparse matrix with different numbers of measurement表1 不同观测次数下不同观测矩阵与稀疏基相关性参数表

由表1可以看出，在相同的观测次数时，自适应感知矩阵与稀疏基相关性最小，满足压缩感知要求的RIP性质。

5.3 特征提取效果对比实验

观测矩阵的设计是压缩感知用于特征提取时重要部分，经过观测矩阵的观测得到的观测值包含图像分类识别的信息，用于神经网络进一步的训练和识别。为此，对不同观测矩阵产生的观测值进行特征提取效果对比，利用相关算法将不同观测值矩阵重构出原始图像。通过比较不同重构图像与原图像的符合度，对比特征信息提取效果。

为了更直观地显示提取效果，本文采用DCT稀疏变换，与Fourier矩阵、高斯随机矩阵和本文自适应矩阵组合特征提取，共同采用正交匹配追踪OMP（Orthogonal Matching Pursuit）算法重构出原图像。实验效果如图5所示。

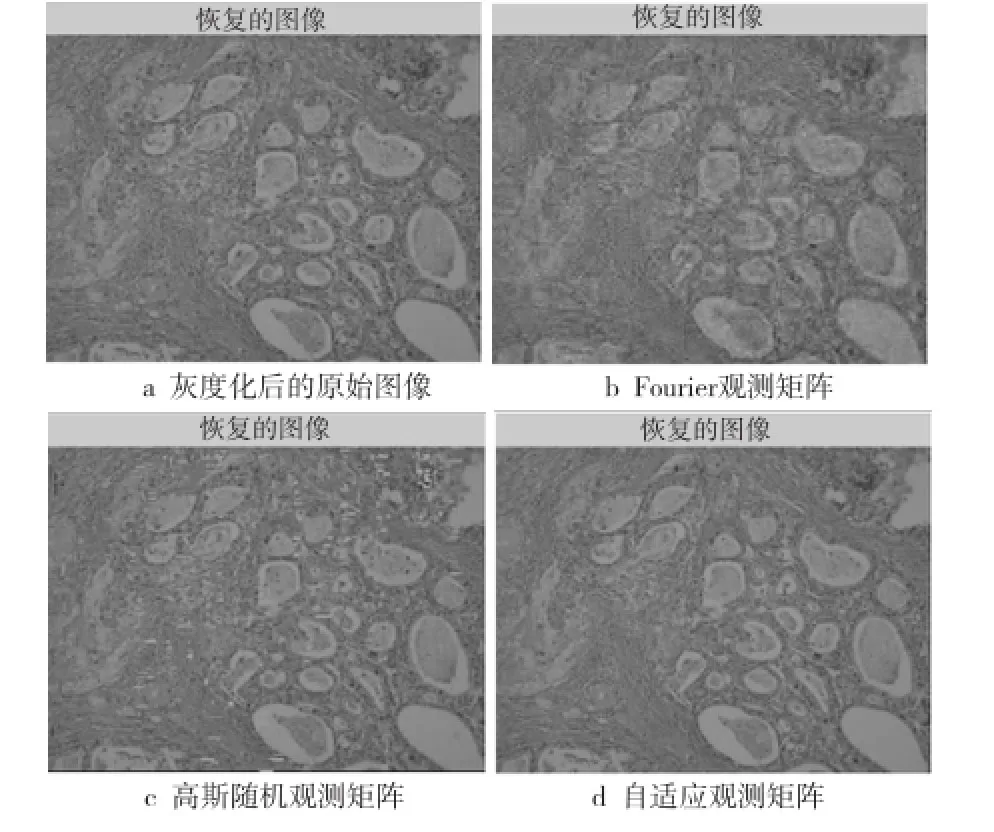
Figure 5 CS reconstructed images图5 压缩感知重构图像

不同观测矩阵观测向量的重构精度如表2所示，其中重构精度以相对误差为参考。

Table 2 Reconstruction precision of different measurement matrixes表2 不同观测矩阵的重构精度表

通过比较明显可以看出，使用Fourier矩阵观测重构的图像相对模糊，使用高斯随机矩阵观测重构的图像干扰信号变多，而使用自适应观测矩阵的观测后的信号重构出的图像相对清晰，和原图像最接近。实验说明通过自适应观测矩阵得到的观测值包含的肿瘤细胞图像识别信息最全面完善。

5.4 识别算法对比实验

将本文方法与常用的一些特征提取和分类算法从算法识别准确率和运行时间两个方面进行性

能对比实验。下面对这些算法参数进行简单说明：一是针对PCA、2DPCA及Bi2DPCA，首先构造输入数据的均值矩阵和总体散布矩阵，求解最佳投影轴，取最佳维数投影获得最优特征基；二是CS中采用DCT稀疏变换和自适应观测矩阵观测得到特征基；三是SVM方法取最佳惩罚参数C为0.2和核函数参数γ为0.04；四是SOFM网络拓扑结构设计，神经元个数为3*20个，训练步长为600，学习速率为0.04。对比实验结果如表3所示。

Table 3 Performance comparison of different recognition algorithms表3 不同识别算法性能对比表

由表3分析，对比CS和SVM相结合的识别算法，本文算法提高了4.2%的识别准确率，减少了2.9 s的运行时间，提高了5.7%的运算速率；而对比常用的PCA和LDA结合的识别算法，更是提高了13.7%的识别准确率，减少了24.9 s的运行时间，提高了41.9%的速率。可见，本文算法相对常用的特征提取和分类识别算法更适合肿瘤细胞的识别，无论是在速率还是准确率上，都有明显的优势。

6 结束语

针对肿瘤细胞图像结构复杂、黏结严重、信息冗余和数据样本少的特点，本文提出一种基于SAM-CS和SOFM结合的分类识别模型。首先利用SAM-CS方法实现对肿瘤细胞图像的特征提取，然后将得到的特征矩阵输入SOFM神经网络，将肿瘤细胞图像较准确地分为正常、增生和癌变三大类。在相同的样本下，该分类识别模型与其他分类识别模型对比，明显具有较高准确率和工作效率。

［1］ Gan Lan，Liu Meng-qing.Gastric epithelial cell adaptive segmentation based on wavelet transform［J］.Computer Engineering and Design，2012，33（7）：2734-2738.（in Chinese）

［2］ Gan Lan，LüWen-ya.Classification of gastric cancer cells based on LLE and LS_SVM［J］.Journal of East China Jiaotong University，2011，28（3）：83-87.（in Chinese）

［3］ Liu Li，Kuang Gang-yao.Overview of image textural feature extraction methods［J］.Journal of Image and Graphics，2009，14（4）：622-635.（in Chinese）

［4］ Li Ling-li.A review on classification algorithms in data mining［J］.Journal of Chongqing Normal University（Natural Science），2011，28（4）：44-47.（in Chinese）

［5］ Chen Guang-hong，Tang Jie，Leng Shuai.Prior image constrained compressed sensing（PICCS）：A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets［J］.Medical Physical，2008，35（2）：660-663.

［6］ Ren Cong-lin.Research of gene expression data classification based on compressive sensing algorithm［D］.Beijing：Beijing Jiaotong University，2012.（in Chinese）

［7］ Ning Wan-zheng，Wang Hai-yan，Shen Xiao-hong，et al.Signal reconstruction algorithm under adaptive measurement matrix［J］.Application Research of Computers，2011，28（9）：3309-3314.（in Chinese）

［8］ Huang Xiao-sheng，Dai Qiu-fang，Cao Yi-qin.Compressive sensing image fusion algorithm based on wavelet sparse basis ［J］.Application Research of Computers，2012，29（9）：3581-3583.（in Chinese）

［9］ Candes E，Romberg J，Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）：489-509.

［10］ Elad C.The restricted isometry property and its implicationsfor compressed sensing［J］.Academy Sciences，2006，346 （9-10）：589-592.

［11］ Michael E.Optimized projections for compressed sensing ［J］.IEEE Transactions on Signal Processing，2007，55 （12）：5695-5702.

［12］ Teuvo K.Self-organizing maps［M］.3rd ed.Berlin：Springer，2001.

［13］ Duan Ming-xiu.Improved CLARA clustering algorithm based on SOFM algorithm［J］.Computer Engineering and Applications，2010，46（22）：210-212.（in Chinese）

附中文参考文献：

［1］ 甘岚，刘梦清.基于小波分析的胃上皮细胞自适应分割算法［J］.计算机工程与设计，2012，33（7）：2734-2738.

［2］ 甘岚，吕文雅.基于LLE和LS_SVM的胃粘膜肿瘤细胞图像分类［J］.华东交通大学学报，2011，28（3）：83-87.

［3］ 刘丽，匡纲要.图像纹理特征提取方法综述［J］.中国图像图形学报，2009，14（4）：622-635.

［4］ 李玲俐.数据挖掘中分类算法综述［J］.重庆师范大学学报（自然科学版），2011，28（4）：44-47.

［6］ 任丛林.基于压缩感知算法的基因表达数据分类的研究［D］.北京：北京交通大学，2012.

［7］ 宁万正，王海燕，申晓红，等.一种自适应观测矩阵下的信号重构算法［J］.计算机应用研究，2011，28（9）：3309-3314.

［8］ 黄晓生，戴秋芳，曹义亲.一种基于小波稀疏基的压缩感知图像融合算法［J］.计算机应用研究，2012，29（9）：3581-3583.

［13］ 段明秀.结合SOFM的改进CLARA聚类算法［J］.计算机工程与应用，2010，46（22）：210-212.

甘岚（1964），女，江西南昌人，教授，研究方向为图像处理和模式识别。E-mail：317659683@qq.com

GAN Lan，born in 1964，professor，her research interests include image processing，and pattern recognition.

孙开杰（1990 ），男，江苏建湖人，硕士生，研究方向为图像处理和模式识别。E-mail：sunkeenjesus@163.com

SUN Kai-jie，born in 1990，MS candidate，his research interests include image processing，and pattern recognition.

谢丽娟（1987 ），女，江西抚州人，硕士，研究方向为图像处理和模式识别。E-mail：304848351@qq.com

XIE Li-juan，born in 1987，MS，her research interests include image processing， and pattern recognition.

Recognition algorithm of gastric epithelium tumor cell images based on SAM-CS and SOFM

GAN Lan，SUN Kai-jie，XIE Li-juan
（College of Information Engineering，East China Jiaotong University，Nanchang 330013，China）

Given the characteristics of serious cementation and information redundancy of gastric epithelium tumor cell images（hereinafter referred to as tumor cell images），we propose an algorithm which is a combination of the compressed sensing of self-adaptive measurement（SAM-CS）matrix and the selforganizing feature map（SOFM）neural network.Firstly，the tumor cell images are transferred to column vectors，then the linear observation vectors are generated through the SAM-CS theory.Finally，we train and classify the linear observation vectors by using the learning algorithm of SOFM neural network to implement the recognition of tumor cell images.Experimental results show that compared with traditional algorithms，the proposed algorithm has improved 4.2%of the recognition accuracy and 5.7%of the operation speed at least.

self-adaptive measurement matrix；compressed sensing；self-organizing feature map；the recognition of tumor cell images

TP391.41

A

10.3969/j.issn.1007-130X.2015.08.021

1007-130X（2015）08-1558-08

2014-08-11；

2014-10-11

国家自然科学基金资助项目（61163040，61402227）；江西省教育厅资助项目（GJJ10451，GJJ14372）

通信地址：330013江西省南昌市华东交通大学信息工程学院

Address：College of Information Engineering，East China Jiaotong University，Nanchang 330013，Jiangxi，P.R.China