一种结合AADL和IMC的系统可靠性建模方法＊

程亦涵，黄志球，阚双龙

（南京航空航天大学计算机科学与技术学院，江苏 南京210016）

1 引言

随着嵌入式软件不断发展，软件开发规模逐渐扩大，软件复杂度不断增加，以及其在汽车、核能、航空、航天等安全关键领域的广泛应用，使人们对嵌入式软件的可靠性和安全性有更高的要求。软件失效所引起的安全事故频发，使保障嵌入式软件的安全性成为近年来软件工程领域的研究热点。为了解决上述问题，出现很多新的方法，其中最突出的就是模型驱动开发MDD（Model Driven Development）［1］。

模型驱动开发是一种以模型为主体的高级别抽象开发方法。模型驱动开发能为各个开发阶段提供全局统一的视图和指导，能在开发早期对模型进行验证，尽早发现错误。常用的MDD 模型有UML、SysML等。

2004年11月，汽车工程师协会SAE（Society of Automotive Engineers）发 布 了 航 空 标 准AS5506，命 名 为AADL（Architecture Analysis and Design Language）［2，3］。AADL是一种应用于嵌入式系统领域的体系结构建模语言，支持航空、航天、汽车等领域复杂实时的安全关键系统的设计与分析。AADL提供了标准化的文本和图形符号以描述软件、硬件系统架构以及其功能接口。同时，AADL支持各种类型的分析，以保障其行为和建模系统性能符合需求。

当定义的初始属性不能满足用户需要时，AADL 引入了附件的概念。附件拥有独立的语法和语义，但必须与AADL核心语义标准保持一致。SAE在2006年发布的AS5506/1标准中提出了错误模型附件（Error Model Annex）［4］，附件通过定义一组声明和语义指明AADL体系结构中组件和连接的错误模型。通过错误模型附件，我们可以对一个AADL体系结构模型的系统属性，如安全性、可靠性、完整性等，进行定性和定量评估。

AADL本身是一个具有确定语义定义并且有严格语法的半形式化建模语言，要对AADL 系统架构模型进行相应的非功能属性分析，还需要对AADL系统架构模型中的构件属性进行形式化描述，然后再借用形式化理论方法和相关工具来验证系统模型的非功能属性是否满足需求。AADL 错误模型附件中提到，含有错误模型的AADL 体系结构模型可以支持多种方式的分析，如故障树可以从规范出发分析其安全性，马尔科夫链分析法可以用于评估其可信性和可用性，但马尔科夫链模型无法对系统构件间的交互行为进行动态的描述。为了对系统构件间的交互行为进行动态的描述，往往需要采用更高级的形式化语言，如广义随机Petri网GSPNs（Generalized Stochastic Petri Nets）［5］。本文采用交互式马尔科夫链IMC（Interactive Markov Chains）［6］对AADL 模型中构件及其错误状态可能的失效进行刻画，建立IMC 可靠性计算模型，通过分析得出原AADL 模型是否满足设计要求。

本文第2节结合已有工作介绍AADL模型分析的相关问题和研究；第3节介绍AADL 可靠性模型及其建立方法；第4节介绍IMC 的交互动作语义，并给出从AADL可靠性模型到IMC 模型的转化规则；第5节结合法国空中交通控制系统的实例，通过第4节的规则，转化得到相应的IMC模型进行定量分析，得到结果反馈给原模型；第6节为总结与展望。

2 相关工作

随着模型驱动开发在工业界广泛应用，很多组织开始基于AADL 模型进行设计与分析研究，并开发了一系列相关设计分析工具。其中，卡内基梅隆大学软件工程研究所SEI（Software Engineering Institute）基于Eclipse平台开发了开源AADL 设计 工 具OSATE［7］。OSATE 提 供 从 前 到 后 对AADL模型进行处理的工具集，可以以XML 文本文件或图形的方式表示AADL 模型文件，并对AADL模型文件进行语法和语义的检查。由于OSATE是开源的，为其他的基于AADL 模型的分析提供了环境。许多研究者以OSATE 环境为基础研究开发针对AADL 模型属性分析的工具，如AADL模型仿真测试工具AADS［8］。类似的建模工具还有STOOD。

在AADL模型可靠性分析方面，Rugina A 在2006年提出AADL 可靠性模型（AADL Dependability Model）。结合AADL 可靠性模型，Rugina A 在文献［5］提出了一种AADL 分析方法，将AADL可靠性模型转化为GSPN，进行形式化分析验证，并设计实现了相关工具ADATP。文献［9］基于Rugina A 的研究，设计了一套完整的工具集对AADL模型进行定性和定量分析。

在AADL模型可靠性方面，国内也有相关研究，文献［10］提出了一种AADL 向马尔科夫链转化的方法，并结合需求，分析模型是否符合要求。文献［11］和文献［12］将AADL 与UPPAAL 验证工具结合，分别验证了AADL 模型的可调度性和行为模型的正确性。文献［13］和文献［14］将AADL可靠性模型转化到GSPN，并设计实现了AADL模型可靠性分析评估工具ARAM。

AS5506/1标准中提到：马尔科夫分析方法可以定量分析错误模型的可信性和可用性。但是，马尔科夫链在描述复杂系统时有自身的局限性：无法描述系统构件之间的交互动作。故上文提到的工作大都将AADL 可靠性模型转化到GSPN，再通过GSPN 内部的分析方法进行定量分析，但GSPN在分析可靠性的时候，仍然需要转化到马科夫链，进行马尔科夫链分析。本文提出一种模型转化方法，将AADL可靠性模型转化到交互式马尔科夫链。由于交互式马尔科夫链是一种功能行为和性能指标混合的并发系统模型，所以它既可以直接进行马尔科夫分析，又可以对模型进行定性分析，为AADL可靠性模型研究提供一种新的思路。

3 AADL可靠性模型研究

AADL可靠性模型由AADL系统架构模型和AADL错误模型组成。系统架构模型从软件、硬件两方面描述系统架构，描述了系统内部组件之间的连接以及相互依赖关系；AADL 错误模型附件定义了构件和连接建立故障模型的声明规则和语义。AADL系统架构模型通过类型（Type）和实现（Implementation）两部分定义整体模型。类型定义了模型的外部可见特性，如接口、属性等；实现定义了模型的内部特性，如交互、子组件等。与AADL系统架构模型一样，AADL 错误模型也是由两部分组成：（1）错误类型（Error Model Type）定义了错误模型的基本要素：错误状态、事件等；（2）错误实现定义了由错误事件和错误传播引起的错误状态之间的变迁。

AADL体系结构模型可以提供组件之间的依赖关系以及与可靠性相关的信息，如故障、失效模式、修复机制、错误传播路径等等，结合错误模型附件的基本错误附录库，可以得出相应的可靠性模型。

错误类型声明一组错误状态（Error State）、错误事件（Error Event）以及错误传播（Error Propagations）。发生（Occurrence）属性表示到达率或者事件或传播发生的概率。错误模型实现声明了错误状态之间的转化（Error Transitions）。图1是一个简单的没有错误传播的错误模型范例。如图1所示，初始状态是无错误状态，错误状态有Erroneous和Failed 两个，分别对应Temp＿Fault和Perm＿Fault两个错误事件，而Restart和Recover则是系统自行修复的事件。

Figure 1 An error model example without propagations图1 简单错误模型

AADL体系结构模型中，不同组件之间存在交互，而组件的错误模型也存在交互。错误模型的交互由组件之间的连接和依赖关系确定。AS5506/1标准将错误传播分为Out－propagation和In－propagation 两 种。Out－propagation 通 过 组件之间的连接和依赖关系将错误传播给其他组件；而In－propagation只会接受相应的组件传播过来的错误。一个Out－propagation 可能会对应多个In－propagation。此时，必须通过组件之间的依赖关系 来 确 定Out－propagation 所 对 应 的In－propagation。图2中，图2a表示在AADL模型中组件1与组件2之间有数据连接；图2b表示组件2对组件1有依赖；图2c表示当错误发生，错误模型中，组件1与组件2之间的依赖关系。由此，我们可以得出对应的带依赖关系的错误模型，并对其进行模型转化，得到相应形式化模型进行验证。

Figure 2 Architecture－based dependency图2 组件之间的依赖关系

图3是组件1对应的错误模型，从图3中我们可以看到，在错误模型类型中，定义了out error propagation属性，表示错误传播，系统需要判断该错误是否发生传播，其发生的概率是固定概率p，而在错误实现中，定义了错误转移发送的信息Erroneous。组件2 的错误模型定义没有在这里提出，它与1唯一的不同是在接收错误的时候，当2接受到组件1发送的错误时，会从Error＿free状态转换到Failed。

Figure 3 An error model example with dependency图3 带有依赖关系的错误模型

在错误模型建立时，我们需要考虑组件之间的相互依赖关系，同时，我们还需要考虑错误模型与系统模型之间的连接，因为错误发生之后，会对系统产生影响（如备用系统的启用等）。在AADL中，通常使用Guard＿Transition属性来连接。

图4所示为错误模型中发生的错误对系统模型产生的影响，其中，g1～g6 行为系统模型通过Guard＿Transition 属性与错误模型相关联。当Comp1 处 于FailedVisible状 态、Comp2 处 于Error＿Free状态时（g1～g3），系统应执行Comp1.Send2和Comp2.Send1，使系统切换到备用组件，反之则应切换回主组件。通过Guard＿Transition属性，错误组件与系统组件相关联，使其能更好地反映错误事件发生对整个系统造成的影响。

当我们得出带有依赖关系的错误模型后，就可以将完整的可靠性模型转化到形式化模型进行验证分析。

Figure 4 Guard＿Transition property associations in the AADL model图4 AADL模型中的Guard＿Transition属性

4 IMC模型以及转换规则

4.1 IMC模型

IMC模型作为一种可以组合化的性能评价模型由德国学着Hermanns H 于1998年提出，其最大的优点是在刻画系统性能特征的同时还提供了对复杂并发系统的组合描述能力，使得对复杂并发系统的性能评价可以得到简化。IMC 模型与其他基于动作的并发系统模型有很大不同，它结合了系统的性能特征，同时又是一个交织语义的模型。IMC模型实际上是标记转移系统LTS（Labeled Transition System）和带标记的连续时间马尔科夫链 labeled CTMC （labeled Continuous－Time Markov Chains）这两个系统的综合。

一个IMC是一个五元组（S，Act，→ ，▶，s0），其中

（1）S是一个非空状态集合。

（2）Act是一个动作集合。

（3）→S×Act×S是一个动作转移关系，通常将（s，a，s′）∈→记 作

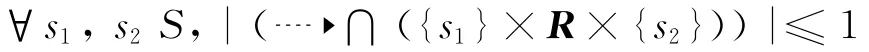
其中，R为转移率矩阵。

（5）S0是初始状态。

定义中的两个转移关系分别是LTS中的动作转移与CTMC中的马尔科夫转移，其含义基本保持不变。（4）中的λ表示转移率，与转移概率不同，转移率λ与时间长短是无关的。这些转移率构成一个转移率矩阵R。由上述定义可以看出，IMC在定义中将LTS与CTMC 的各部分元素基本上是没有改变地结合在一起，这样就最大可能地保持了LTS和CTMC 两个系统原有的性质。图5 是一个简单的IMC图示。

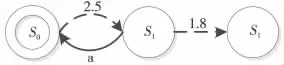
Figure 5 An example of interactive Markov chains图5 交互式马尔科夫链图示

两种系统的结合，使得IMC 可以更加全面地描述一个复杂嵌入式系统，特别是描述并行系统。图6中P和Q是两个简单的操作：（1）P从s0开始，经过参数为λ马尔科夫转移到达状态s1，再执行动作a到达s2；（2）Q与P类似，也需要执行动作a，到达最终状态。当P与Q并行执行的时候，即图6所示的P‖aQ，IMC 完美地解决了并行执行的问题。

Figure 6 Icon of IMC parallel execution图6 IMC并行执行图示

4.2 转化规则

本文选用IMC 模型作为系统可靠性计算模型，并建立AADL可靠性模型与IMC 模型之间的对应转化关系。主要通过以下两步来完成：（1）基本元素之间的对应转化；（2）相关组件之间的inout propagation转化到对应IMC模型。

4.2.1 基本元素对应转化

AADL模型与IMC模型之间基本元素的转化是比较简单的，因为AADL 错误模型通常表示成一个随机自动机，一个组件只作为一个状态。表1是基本元素之间的转化规则。

Table 1 Basic AADL error model to IMC transformation rules表1 AADL模型基本元素与IMC的对应转化

有了上述基本元素转化关系，我们可以将之前图1中提到的简单的错误模型转化到IMC 模型，具体如图7所示。

Figure 7 Corresponding IMC model to the error model in figure 1图7 图1所示简单错误模型对应的IMC模型

4.2.2 In－out propagation 转换规则

前文中我们提到，Error Model Annex中定义了AADL模型中的错误传播，用In－out propagation来表示。Out－propagation表示错误向组件外传播，并到达指定接收组件即In－propagation。一个Out－propagation可以对应多个In－propagation，通过组件之间的依赖关系，我们可以得出相应的带依赖关系的错误模型（如图3所示），根据名称匹配找到与Out－propagation相对应的In－propagation。如图8 所示，组件1 作为发送者，向外传播名为Error的错误，而组件2作为接收者接收一个错误传播，名为Error。这样两个组件为一对In－out propagation。

在定义In－out propagation转化规则的时候，首先要将Out与In区分开。因为如果Out－propagation发生，则接收组件一定能接收到传播过来的错误信息。图9 是带有传播的错误模型转化到IMC模型的范例。Sender发生错误后，有一定概率将这个错误传播出去，根据依赖关系，该错误信息将发送给Receiver，收到错误信息之后，Receiver从Error＿Free状态转换到Failed状态。

5 实例分析

本文将结合法国空中交通控制系统，先建立AADL可靠性模型，再通过上述模型转换规则得到IMC模型，并对其进行可靠性分析，通过结果对原系统两种备选方案选择提出参考。

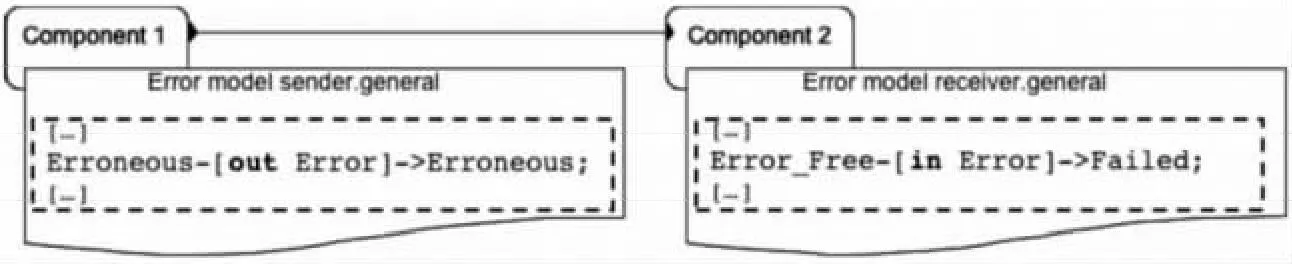
Figure 8 Sender and receiver—name matching propagations图8 错误传播中的名称匹配

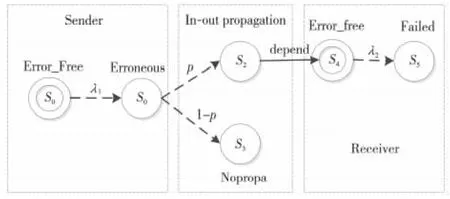
Figure 9 IMC model with propagations图9 带有传播的IMC模型

5.1 系统AADL模型

如图10所示，该系统是由两个分布式软件组件集合组成：飞行计划（flight plans，FPunit）和雷达数据（radar data，RDunit）。建立体系结构模型有a、b两种方案。FPunit与RDunit内部结构相同：都拥有两个线程Comp1（主要）和Comp2（备用），这是为了提高系统的可靠性和安全性，在设计FPunit和RDunit构件时加入了冗余构件，即这两个构件存在备用线程（Comp2），在主要线程（Comp1）出现故障时会自动切换到备用构件继续完成功能。a 和b 两个方案都使用两个处理器（processor1和processor2）。

a和b的区别在于：方案a中，RD＿Comp1 和FP＿Comp1分别由不同的处理器处理（RD＿Comp1与Processor2 绑 定，FP＿Comp1 与Processor1 绑定）；而方案b中，RD＿Comp1 和FP＿Comp1 绑定同一个处理器。整个系统有两个操作状态：正常和重配置。两个处理器通过总线相连。当总线出现错误时，会导致RDunit出现故障从而导致系统失效，而RDunit会从FPunit接收错误传播。

5.2 依赖关系分析及错误模型的建立

组件之间的依赖关系主要来源于它们之间的交互，根据上面的体系结构图，可以得出如下依赖关系：

（1）处理器与其运行的线程之间有结构依赖关系。图10a中的S1、S2、S3和S4反映这种依赖关系。

（2）同时，处理器与其运行的线程还有恢复依赖关系。如果一个线程出错，则正在运行错误状态的处理器不能重启。图10a中的R1、R2、R3和R4反映这种依赖关系。

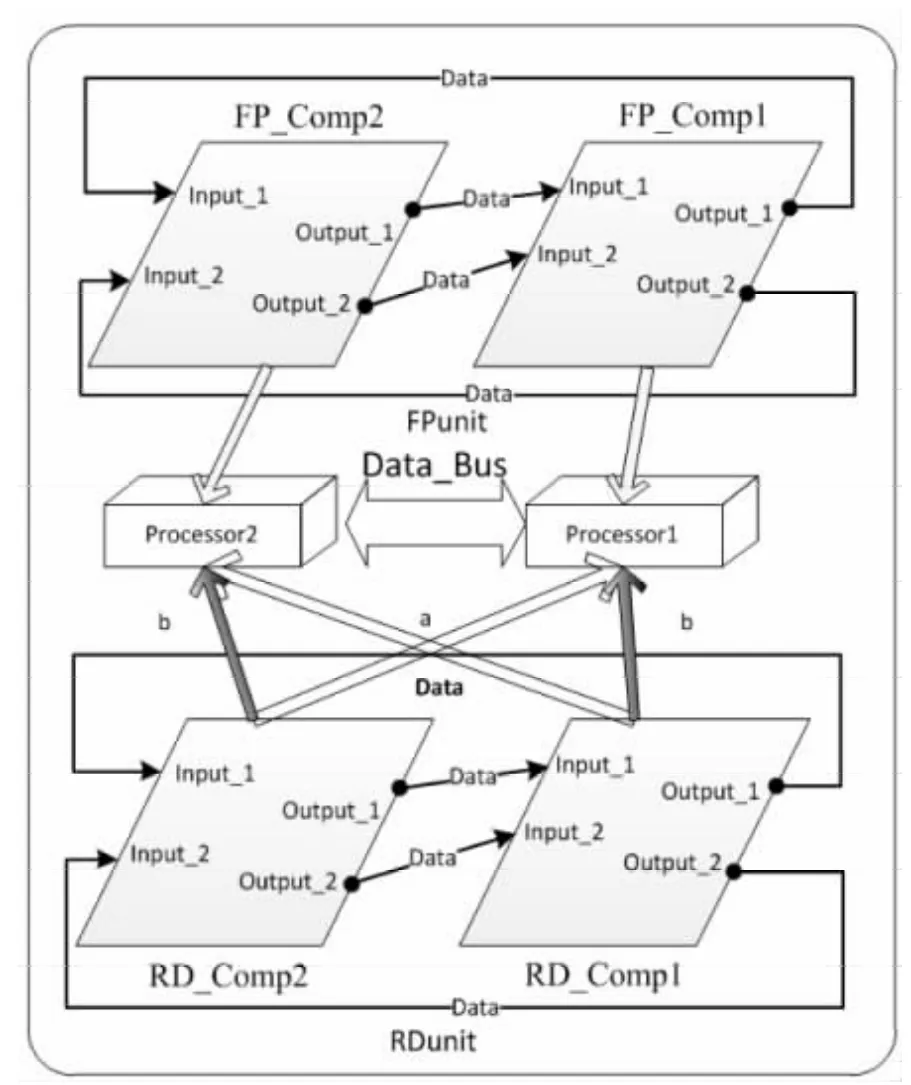
Figure 10 Two candidate AADL architecture models of the air traffic control system图10 空中交通控制系统的两个备选AADL体系结构模型

（3）两个处理器之间还有维护依赖性，但图10中并未体现这一点。

（4）图10 中 的FT1 和FT2 反 映 了 两 个 线 程之间的错误容忍依赖：当一个线程出现错误，可以切换到另一个正常线程，保证系统继续运行。

（5）图10b中F3反映了总线和线程之间的结构依赖。当总线出错，会断开与线程之间的连接，使其可以从正常状态切换到重配置状态，完成相应的功能。

（6）FPunit与RDunit之间有功能依赖关系，FPunit出现错误之后可能会将错误传播给RDunit，图10中的F1和F2反映这个依赖关系。相反，RDunit出现错误却不会传播给FPunit，这在建立错误模型时尤为关键。

根据上述依赖关系，我们可以建立对应错误模型。为了简化整个模型，我们重点关注FPunit和RDunit之间的依赖关系，不考虑处理器内部的情况。图11为FPunit线程的错误模型，f1、f2对应FPunit和RDunit之间的功能依赖关系（图10 中的F1和F2），t1～t4对应线程中的错误容忍依赖（图10中的FT1和FT2）。根据依赖关系，该组件可能会向外传播错误，但并不能接收外来错误。

5.3 模型转化及结果分析

图12是上述错误模型根据之前提到的转化规则转化得到的IMC 模型，其中，Restart示线程重启，重新回到Error＿Free状态。图13 中，该事件的发生也对系统产生影响：当FP＿Comp1 发生错误，系统则使用备用操作模块FP＿Comp2；当FP＿Comp1重启之后，回到Error＿Free状态，系统重新使用主要操作模块FP＿Comp1。FP＿Comp2 向RDunit传播错误的部分与FP＿Comp1相同，所以我们将其省略。

表2是图中对应的转换率和概率的具体数值，λc是总线的故障率。通过图12的IMC模型，结合IMC分析方法，可以得出两种备选方案的故障率与总线故障率λc的关系，如表3所示。从结果中可以看出，当λc＜10－5/h时，两种备选方案的故障率比较接近；当λc＞10－5/h时，方案a相较方案b，故障率明显提高。这是因为方案b在正常情况下，FPunit与RDunit处于同一台处理器，数据处理不经过总线，受总线故障影响较小。所以，当总线故障率λc＞10－5/h时，选用方案b比较合适。

Figure 11 Error model of the FPunit图11 FPunit的错误模型

Figure 12 IMC model of the system图12 系统IMC模型

Table 2 Nominal value of the transition rates表2 AADL转换率的标准值

Table 3 Experimental results表3 实验结果

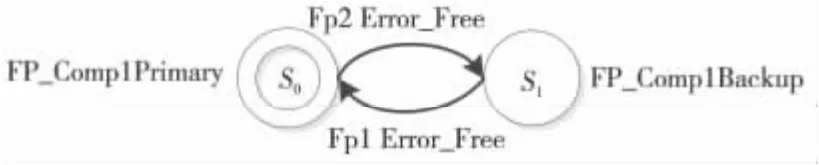
Figure 13 Impact of errors on the system model图13 错误对系统模型产生的影响

6 结束语

本文提出了一种从AADL可靠性模型向IMC模型转化的方法，并给出具体的转化规则。以这些规则为基础，通过一个空中交通控制系统的实例，证明转化规则的可用性；对AADL可靠性模型进行了定量分析，对系统模型的建立提出参考意见，也给AADL可靠性模型分析提供了一种新的思路。

虽然本文在AADL可靠性模型分析上提出了一种创新，提出了新的转化规则，但是AADL语言还在不断更新其语法标准，添加新的语法元素和规则。后期的工作和研究重点在于随着AADL标准的更新扩充相应的AADL 可靠性模型到IMC 计算模型的模型转换规则。同时，这种转换方法尚未实现自动化，这也是今后工作的重点。

［1］ OMG.Model driven architecture（MDA）［EB/OL］.［2010－07－03］.http：//www.omg.org/mda/.

［2］ Feiler P H，Gluch D P，Hudak J J.The architecture analysis＆design language（AADL）：An introduction：CMU/SEI－2006－TN－011［R］.Pittsburgh：Carnegie－Mellon University，2006.

［3］ Yang Z B，Pi L，Hu K，et al.AADL：An architecture design and analysis language for complex embedded real－time systems［J］.Journal of Software，2010，21（5）：899－915.（in Chinese）

［4］ SAE－AS5506/1：SAE architecture analysis and design language（AADL）Annex vol.1，Annex E：Error Model Annex［Z］.Warrendale，PA，USA：International Society of Automotive Engineers，2006.

［5］ Rugina A E，Kanoun K，Kaaniche M.A system dependability modeling framework using AADL and GSPNs［M］∥Architecting Dependable Systems IV.Berlin：Springer，2007：14－38.

［6］ Hermanns H.Interactive Markov chains and the quest for quantified quality［M］.Berlin，Germany：Springer－Verlag，2002.

［7］ SEI AADL Team.An extensible open source AADL tool environment（OSATE）［EB/OL］.［2006－06－02］.http：//la.sei.cmu.edu/aadl/downloads/osate13/AADLTooIUserGuide1.3.0%202006－06－02.pdf.

［8］ Varona－Gómez R，Villar E.AADL simulation and performance analysis in SystemC［C］∥Proc of the 14th IEEE International Conference on Engineering of Complex Computer Systems，2009：323－328.

［9］ Hecht M，Lam A，Vogl C.A tool set for integrated software and hardware dependability analysis using the architecture analysis and design language（AADL）and error model annex［C］∥Proc of the 16th IEEE International Conference on Engineering of Complex Computer Systems（ICECCS），2011：361－366.

［10］ Wang Geng，Zhou，Xing－she，Zhang Fan，et al.Research on model－based testing on AADL［J］.Computer Science，2009，36（11）：127－130.（in Chinese）

［11］ LI Zhen－song，Gu Bin.Research on verification method of AADL behavior model based on UPPAAL［J］.Computer Science，2012，39（2）：159－161.（in Chinese）

［12］ Liu Q，Gui S L，Li Y.Schedulability verification of AADL model based on UPPAAL［J］.Computer Applications，2009，29（7）：1820－1824.（in Chinese）

［13］ Zhang C，Yang Z，Dong Y.Research and assessment of the reliability of a fault tolerant model using AADL［C］∥Proc of Advanced Software Engineering and its Applications，2008：45－52.

［14］ Dong Y W，Wang G R，Zhang F，et al.Reliability analysis and assessment tool for AADL model［J］.Journal of Software，2011，22（6）：1252－1266.（in Chinese）

附中文参考文献：

［3］ 杨志斌，皮磊，胡凯，等.复杂嵌入式实时系统体系结构设计与分析语言：AADL［J］.软件学报，2010，21（5）：899－915.

［10］ 王庚，周兴社，张凡，等.AADL 模型的测试方法研究［J］.计算机科学，2009，36（11）：127－130.

［11］ 李振松，顾斌.基于UPPAAL 的AADL 行为模型验证方法研究［J］.计算机科学，2012，39（2）：159－161.

［12］ 刘倩，桂盛霖，李允，等.基于UPPAAL的AADL模型可调度性验证［J］.计算机应用，2009，29（7）：1820－1824.

［14］ 董云卫，王广仁，张凡，等.AADL 模型可靠性分析评估工具［J］.软件学报，2011，22（6）：1252－1266.